はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、4.2節の内容です。ロジスティックシグモイド関数・ロジット関数・ソフトマックス関数について確認します。
【前節の内容】
【他の節一覧】
【この節の内容】
4.2.0 事後確率とロジスティックシグモイド関数・ソフトマックス関数の関係
ロジスティックシグモイド関数・ロジット関数・ソフトマックス関数と事後分布の関係を確認します。
作図に利用するパッケージを読み込みます。
# 4.2.0項で利用するパッケージ library(tidyverse)
・基本事項の確認
この項で登場する確率の基本的なルールを簡単に確認しておきます。
クラス$k$を$C_k$、クラス$k$となる確率を$p(C_k)$で表します。
クラス$k$のとき$\mathbf{x}$となる確率を$p(\mathbf{x} | C_k)$で表し、条件付き確率で定義されます。
この式の両辺に$p(C_k)$を掛けると、同時確率・結合確率になります。
結合確率を全てのクラス$k = 1, \cdots, K$で和をとると、周辺確率になります。
クラス数が$K = 2$のときは
となります。
・ロジスティックシグモイド関数
クラス数が2の場合の各クラスの事後確率からロジスティックシグモイド関数を導出します。
条件付き確率の定義より、結合確率$p(\mathbf{x}, C_1)$を周辺確率$p(\mathbf{x})$で割ると、クラス$C_1$の事後確率$p(C_1 | \mathbf{x})$が得られます。
この関係をベイズの定理と呼びます。
$p(C_1 | \mathbf{x})$は、データ$\mathbf{x}$から学習したクラス$C_1$となる確率と言えます。このとき、学習前の確率$p(C_k)$を事前確率と言います。
次のようにおき、事後確率がロジスティックシグモイド関数になるのを確認します。
対数の性質$\ln \frac{x}{y} = \ln x - \ln y$なので、符号を反転させる(-1を掛ける)と分母分子が入れ替わります。
指数をとります。指数と対数は打ち消し合うので、$\exp(\ln x) = x$です。
$1 = \frac{p(\mathbf{x} | C_1) p(C_1)}{p(\mathbf{x} | C_1) p(C_1)}$を加えます。
逆数をとります。
事後確率の式になるのを確認できました。
この式を次のようにおきます。
この式で定義される関数を、ロジスティックシグモイド関数またはシグモイド関数と言います。
ロジスティックシグモイド関数の出力$\sigma$は、$0 < \sigma < 1$になるので、確率の定義を満たします(確率と解釈できます)。
ロジスティックシグモイド関数をグラフで確認します。
# ロジスティックシグモイド関数を計算 sigmoid_df <- tidyr::tibble( a = seq(-10, 10, by = 0.05), # x軸の範囲を指定 sigma = 1 / (1 + exp(-a)) ) # ロジスティックシグモイド関数を作図 ggplot(sigmoid_df, aes(x = a, y = sigma)) + geom_line() + labs(title = "Logistic Sigmoid Function", y = expression(sigma))
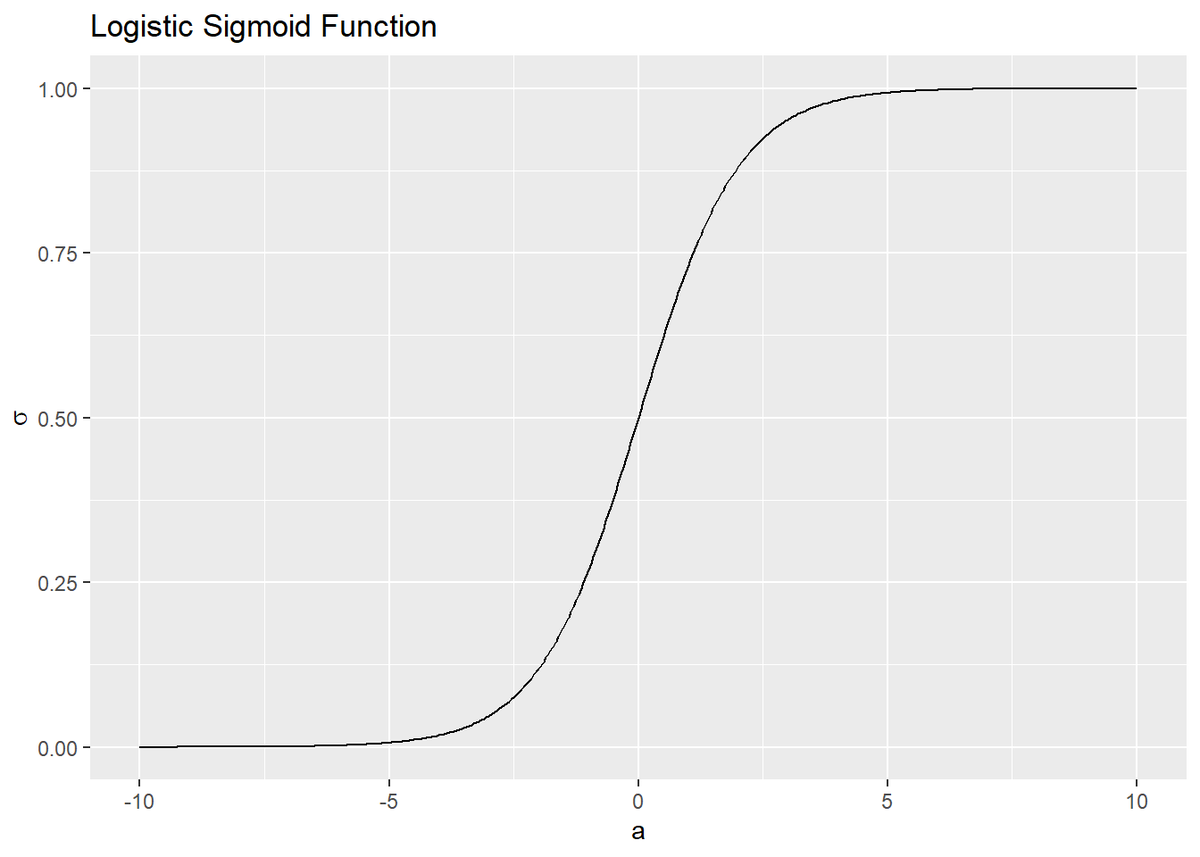
出力(y軸の値)$\sigma$が0から1の値になるのを確認できます。入力$a$の値が小さいと出力は0に近い値(ほぼ0)に、大きいと1に近い値(ほぼ1)になります。このことから、入力を0から1の区間に押し込むと表現されます。
・対称性
ロジスティックシグモイド関数は、点$(0, 0.5)$で点対称な関数です。これを数式とグラフで確認します。
ロジスティックシグモイド関数(4.59)の右辺に$1 = \frac{\exp(a)}{\exp(a)}$を掛けます。
指数の性質より、$e^a e^{-a} = a^{a-a} = a^0 = 1$です。
右辺の分子に$0 = 1 - 1$を足します。
$-a$を入力としたロジスティックシグモイド関数$\sigma(-a) = \frac{1}{1 + \exp(-(-a))} = \frac{1}{1 + \exp(a)}$で置き換えます。
$\sigma(a)$を右辺に、$\sigma(-a)$を左辺に移項します。
式(4.60)の関係が得られました。
この関係式をグラフで確認します。
・作図コード(クリックで展開)
# シグモイド関数を作成 sigmoid <- function(a) { y <- 1 / (1 + exp(-a)) return(y) } # 入力の値を指定 a <- 2 # 対称性をグラフで確認 ggplot(sigmoid_df, aes(x = a, y = sigma)) + geom_line() + # シグモイド関数 geom_vline(xintercept = -a, alpha = 0.5, linetype = "dashed") + # x = -aの補助線 geom_vline(xintercept = a, alpha = 0.5, linetype = "dashed") + # x = aの補助線 geom_linerange(x = -a, ymin = sigmoid(-a), ymax = 1, color = "red") + # 1 - σ(-a)の線分 geom_linerange(x = a, ymin = 0, ymax = sigmoid(a), color = "red") + # σ(a)の線分 scale_x_continuous(breaks = c(-a, a), labels = c("-a", "a")) + # x軸ラベル labs(title = "Logistic Sigmoid Function", subtitle = paste0("a=", a), x = "x", y = "y") # 対称性をグラフで確認 ggplot(sigmoid_df, aes(x = a, y = sigma)) + geom_line() + # シグモイド関数 geom_vline(xintercept = -a, alpha = 0.5, linetype = "dashed") + # x = -aの補助線 geom_vline(xintercept = a, alpha = 0.5, linetype = "dashed") + # x = aの補助線 geom_linerange(x = -a, ymin = 0, ymax = sigmoid(-a), color = "red") + # σ(-a)の線分 geom_linerange(x = a, ymin = sigmoid(a), ymax = 1, color = "red") + # 1 - σ(a)の線分 scale_x_continuous(breaks = c(-a, a), labels = c("-a", "a")) + # x軸ラベル labs(title = "Logistic Sigmoid Function", subtitle = paste0("a=", a), x = "x", y = "y")
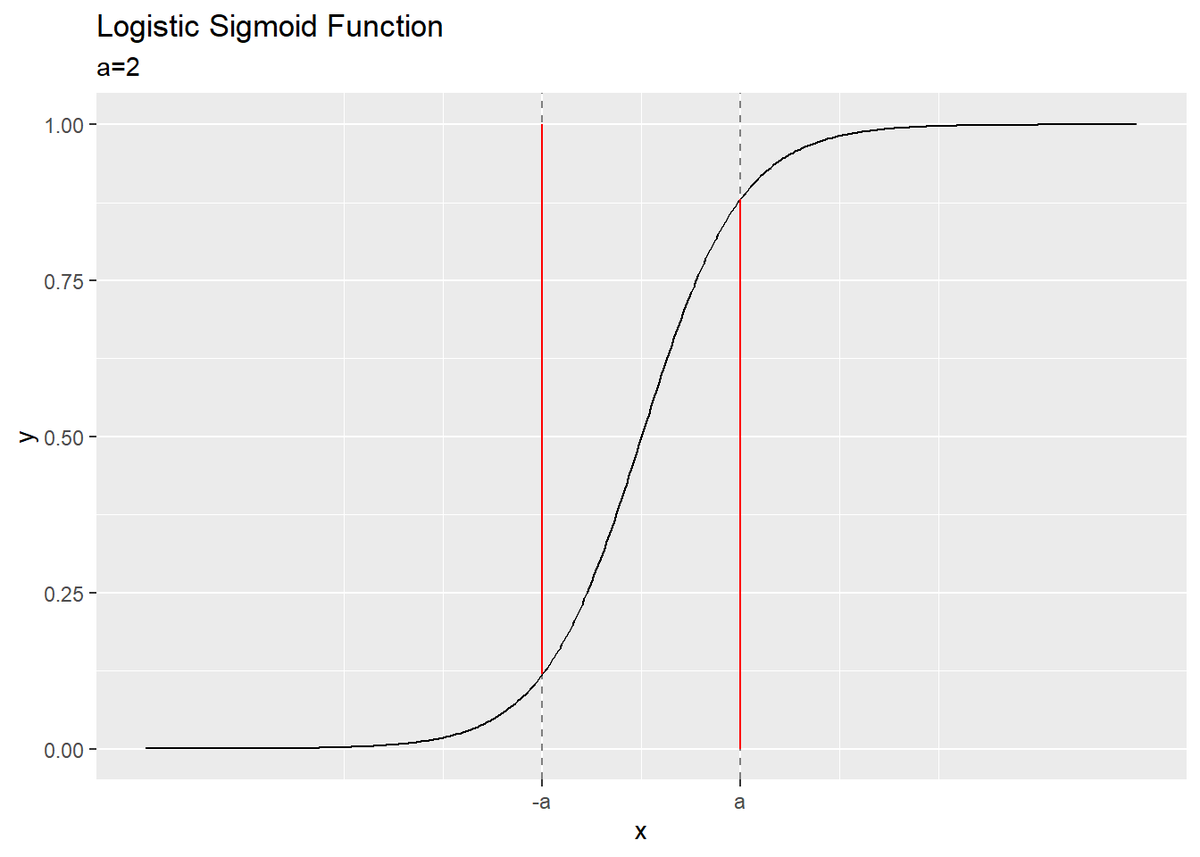
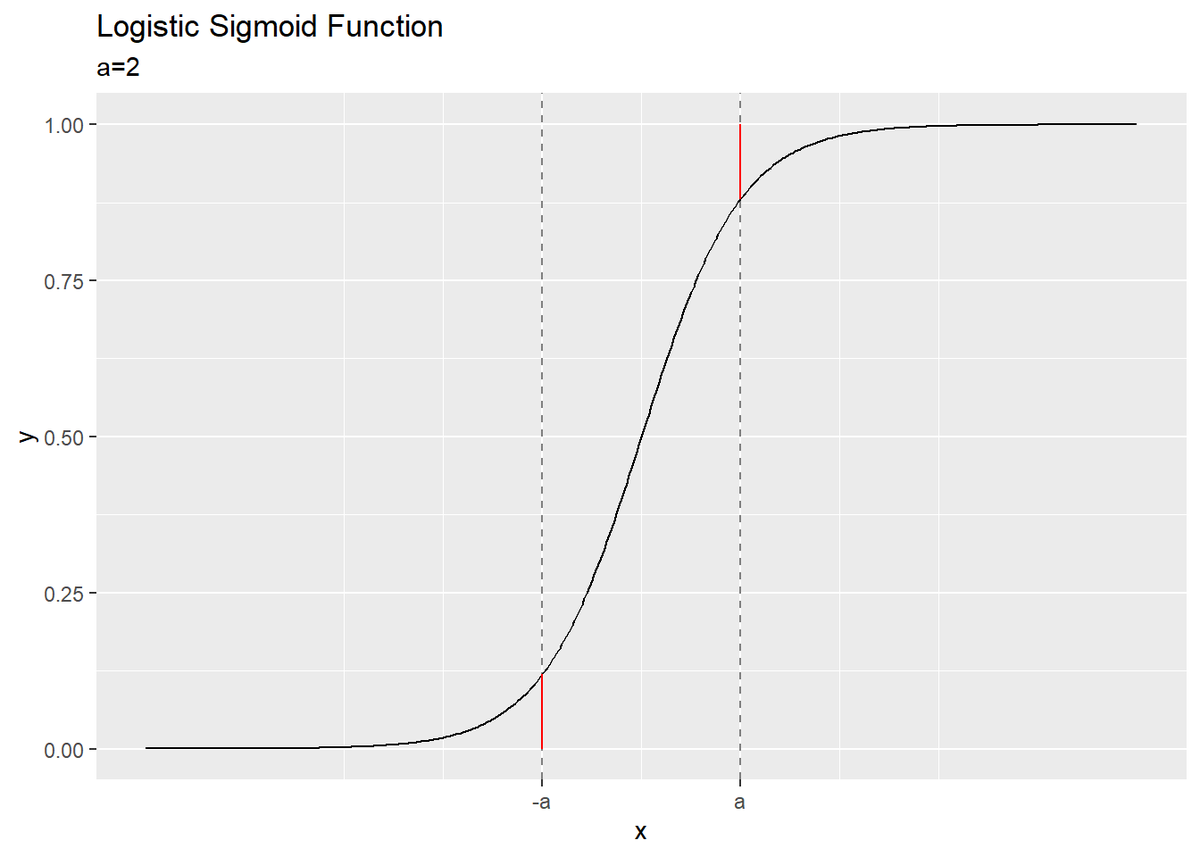
曲線上の点$(a, \sigma(a))$を考えます。$\sigma(a)$は$x = a$における0から曲線までのサイズ(高さ?長さ?距離?)、$1 - \sigma(a)$は曲線から1までのサイズと言えます。
点$(-a, \sigma(-a))$についても同様です。
式(4.60')(4.60)の両辺は、それぞれ赤色の線分に対応おり、そのサイズが一致します。(こういう理解でいいんだよね?)
・ロジット関数
ロジスティックシグモイド関数とロジット関数が逆関数の関係であるのを導出します。
ロジスティックシグモイド関数の出力を$\sigma$とおき、$a$について解きます。
逆数をとります。
$1 = \frac{\sigma}{\sigma}$を引きます。
対数をとります。
符号を反転させて、分母分子を入れ替えます。
ロジット関数の式になるのを確認できました。逆順に式変形すると、ロジット関数からロジスティックシグモイド関数を導出できます。
この式
で定義される関数を、ロジット関数と言います。定義式を見ると、自然対数関数になっているので、丸括弧の中が0より大きい値である必要があります。よって、ロジット関数の入力$\sigma$は、$0 < \sigma < 1$である必要があります。
ある確率$p$について$\frac{p}{1 - p}$をオッズ比と言います。ロジット関数は、式の形が対数をとったオッズ比なので、対数オッズとも言います。
ロジット関数をグラフで確認します。
# ロジット関数を計算 logit_df <- tidyr::tibble( sigma = seq(0.01, 0.99, by = 0.01), # 入力の範囲 a = log(sigma / (1 - sigma)) ) # ロジット関数を作図 ggplot(logit_df, aes(x = sigma, y = a)) + geom_line() + labs(title = "Logit Function", x = expression(sigma))
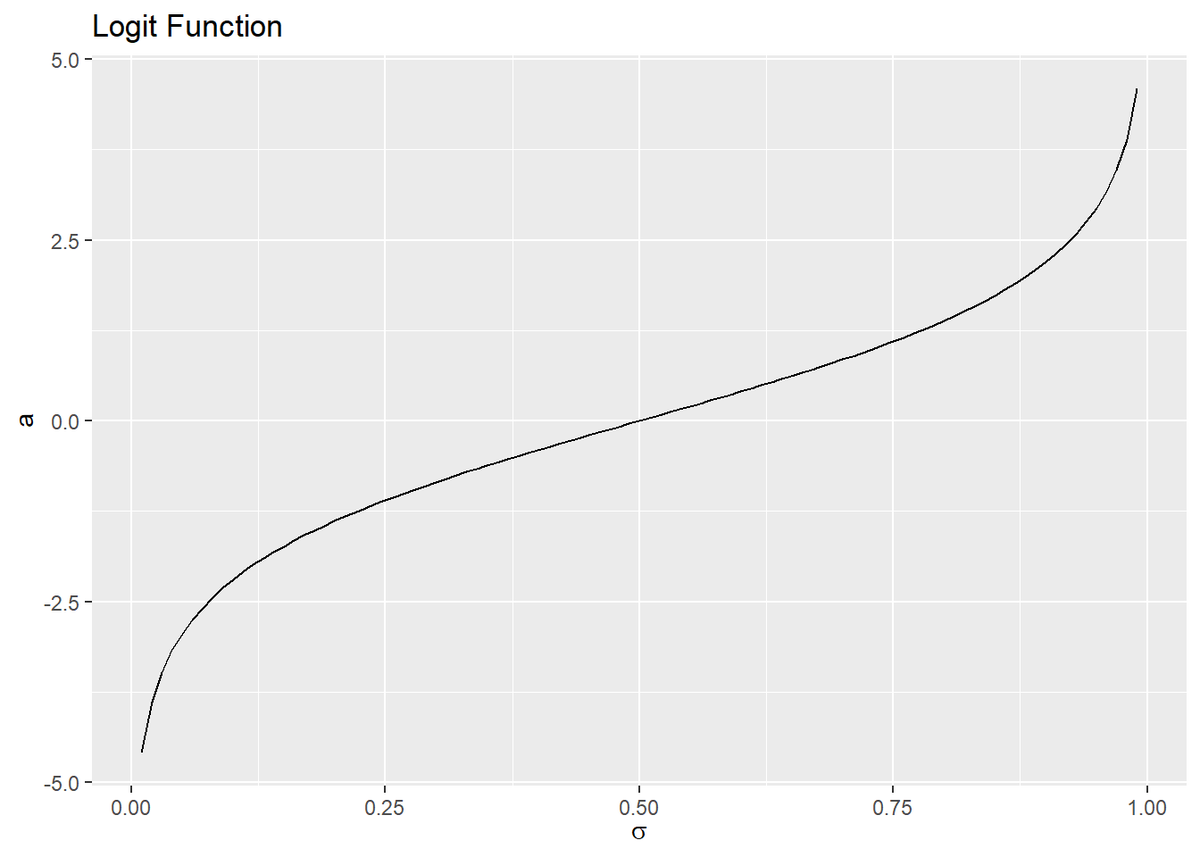
入力(x軸の値)$\sigma$が0から1の値なのを確認できます。ロジスティックシグモイド関数とロジット関数のグラフは、$a = \sigma$の直線で回転したグラフになっています。
・ソフトマックス関数
クラス数が$K$の場合の各クラスの事後確率からソフトマックス関数を導出します。
ロジスティックシグモイド関数のときと同様に、結合確率$p(\mathbf{x} | C_k)$を周辺確率$p(\mathbf{x})$で割ると、クラス$C_k$の事後確率$p(C_K | \mathbf{x})$が得られます。
次のようにおき、事後確率がソフトマックス関数になるのを確認します。
指数をとります。
$k = 1, \cdots, K$の和をとります。
1つ上の式をこの式で割ります。
事後確率の式になるのを確認できました。
この式を次のようにおきます。
この式で定義される関数を、正規化指数関数またはソフトマックス関数と言います。
ソフトマックス関数の出力$y_k$は、$0 < y_k < 1$、$\sum_{k=1}^K y_k = 1$になるので、$\mathbf{y} = (y_1, \cdots, y_K)$は確率分布の定義を満たします(確率分布と解釈できます)。
正規化される理由やグラフについてはこの記事を参照してください。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
3章の途中なのですが、試しに読んでみたらサクッとできたので更新しておきます。
2021年12月3日は、ハロー!プロジェクトのユニット「SeasoningS」の3人の加入3周年の日です!!!
公開されているMVとかないので代わりにこれを貼っておきます。
music.apple.com フルで聴いてほしい、、、もっと曲が増えてほしい。
【次節の内容】

