はじめに
機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に、理解の助けになったことや勉強会用レジュメのまとめです。
この記事では、R言語でトピックモデルをギブスサンプリングによって推定する方法について書いています。Rの基本的な関数で参考書のアルゴリズム4.3を組むことで、理論をコード・処理の面から理解しようというものです。
パラメータの更新式の導出などはこの記事をご参照ください。
【前節の内容】
【他の節の内容】
【この節の内容】
・コード全体
・テキスト処理
# 利用パッケージ library(RMeCab) library(tidyverse) ### テキスト処理 # テキストファイルの保存先を指定する file_path <- "フォルダ名" # 抽出しない単語を指定 stop_words <- "[a-z]" # 小文字のアルファベットを含む語 # 形態素解析 mecab_df <- docDF(file_path, type = 1) # 文書dの語彙vの出現回数(N_dv)の集合 N_dv <- mecab_df %>% filter(grepl("名詞|形容詞|^動詞", POS1)) %>% # 抽出する品詞(大分類)を指定する filter(grepl("一般|^自立", POS2)) %>% # 抽出する品詞(細分類)を指定する filter(!grepl(stop_words, TERM)) %>% # ストップワードを除く select(-c(TERM, POS1, POS2)) %>% # 数値列のみを残す filter(apply(., 1, sum) >= 5) %>% # 抽出する総出現回数を指定する t() # 転置 # 確認用の行列名 dimnames(N_dv) <- list(paste0("d=", 1:nrow(N_dv)), # 行名 paste0("v=", 1:ncol(N_dv))) # 列名 # 文書dの単語数(N_d)のベクトル N_d <- apply(N_dv, 1, sum) # 行方向に和をとる # 文書数(D) D <- nrow(N_dv) # 総語彙数(V) V <- ncol(N_dv)
・パラメータの初期設定
### パラメータの初期設定 # トピック数(K) K <- 4 # 任意の値を指定する # ハイパーパラメータ(alpha, beta) alpha_k <- rep(2, K) # 任意の値を指定する beta <- 2 # 任意の値を指定する # 文書dの語彙vに割り当てられたトピック(z_dn)の集合 z_dn <- array(0, dim = c(D, V, max(N_dv)), dimnames = list(paste0("d=", 1:D), paste0("v=", 1:V), paste0("N_dv=", 1:max(N_dv)))) # 文書dにおいてトピックkが割り当てられた単語数(N_dk)の集合 N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) # 文書全体でトピックkが割り当てられた語彙vの出現回数(N_kv)の集合 N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), paste0("v=", 1:V))) # 全文書でトピックkが割り当てられた単語数(N_k)のベクトル N_k <- rep(0, K)
・ギブスサンプリング
### ギブスサンプリング # 受け皿の用意 p <- NULL # 結果の確認用 trace_alpha <- as.matrix(alpha_k) trace_beta <- beta for(i in 1:1000) { ## 新たに割り当られたトピックに関するカウントを初期化 new_N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) new_N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), paste0("v=", 1:V))) new_N_k <- rep(0, K) for(d in 1:D) { ## 文書:1,...,D for(v in 1:V) { ## 各語彙:1,...,V if(N_dv[d, v] > 0) { ## 出現回数:N_dv > 0のときのみ for(ndv in 1:N_dv[d, v]) { ## 各語彙の出現回数:1,...,N_dv # 現ステップの計算のためにカウントを移す tmp_N_dk <- N_dk tmp_N_kv <- N_kv tmp_N_k <- N_k if(z_dn[d, v, ndv] > 0) { # 初回を飛ばす処理 # 前ステップで文書dの語彙vに割り当てられたトピックを`k`に代入 k <- z_dn[d, v, ndv] # 文書dの語彙vの分のカウントを引く tmp_N_dk[d, k] <- N_dk[d, k] - 1 tmp_N_kv[k, v] <- N_kv[k, v] - 1 tmp_N_k[k] <- N_k[k] - 1 } for(k in 1:K) { ## 各トピック # サンプリング確率を計算 tmp_p_alpha <- tmp_N_dk[d, k] + alpha_k[k] tmp_p_beta_numer <- tmp_N_kv[k, v] + beta tmp_p_beta_denom <- tmp_N_k[k] + beta * V p[k] <- tmp_p_alpha * tmp_p_beta_numer / tmp_p_beta_denom } # サンプリング tmp_z_dn <- rmultinom(n = 1, size = 1:K, prob = p) z_dn[d, v, ndv] <- which(tmp_z_dn == 1) # 新たに割り当てられたトピックを`k`に代入 k <- z_dn[d, v, ndv] # 文書dの語彙vの分のカウントを加える new_N_dk[d, k] <- new_N_dk[d, k] + 1 new_N_kv[k, v] <- new_N_kv[k, v] + 1 new_N_k[k] <- new_N_k[k] + 1 } ## /各語彙の出現回数:1,...,N_dv } ## /出現回数:N_dv > 0のときのみ } ## /各語彙:1,...,V } ## /各文書:1,...,D # トピック集合とカウントを更新 N_dk <- new_N_dk N_kv <- new_N_kv N_k <- new_N_k # ハイパーパラメータ(alpha)の更新 tmp_alpha_numer1 <- apply(digamma(t(N_dk) + alpha_k), 1, sum) # 分子 tmp_alpha_numer2 <- D * digamma(alpha_k) # 分子 tmp_alpha_denom1 <- sum(digamma(N_d + sum(alpha_k))) # 分母 tmp_alpha_denom2 <- D * digamma(sum(alpha_k)) # 分母 alpha_k <- alpha_k * (tmp_alpha_numer1 - tmp_alpha_numer2) / (tmp_alpha_denom1 - tmp_alpha_denom2) # ハイパーパラメータ(beta)の更新 tmp_beta_numer1 <- sum(digamma(N_kv + beta)) # 分子 tmp_beta_numer2 <- K * V * digamma(beta) # 分子 tmp_beta_denom1 <- V * sum(digamma(N_k + beta * V)) # 分母 tmp_beta_denom2 <- K * V * digamma(beta * V) # 分母 beta <- beta * (tmp_beta_numer1 - tmp_beta_numer2) / (tmp_beta_denom1 - tmp_beta_denom2) # 結果の確認用 trace_alpha <- cbind(trace_alpha, as.matrix(alpha_k)) trace_beta <- c(trace_beta, beta) }
・コードの解説
・利用パッケージ
# 利用パッケージ library(RMeCab) library(tidyverse)
形態素解析のためのRMeCab::docDF()と、グラフ作成時のtidyr::gather()、ggplot2関連の関数以外にライブラリの読み込みが必要なのはdplyrのみ。(面倒なのでtidyversパッケージを読み込んでいる)
その他テキスト処理の部分は3.3節の記事をご参照ください。
・パラメータの初期設定
・トピック数
# トピック数(K) K <- 4 # 任意の値を指定する
任意のトピック数を指定する。
・ハイパーパラメータ
# ハイパーパラメータ(alpha, beta):一様 alpha <- 2 # 任意の値を指定する beta <- 2 # 任意の値を指定する # ハイパーパラメータ(alpha, beta):多様 alpha_k <- rep(2, K) # 任意の値を指定する beta_v <- rep(2, V) # 任意の値を指定する
任意のハイパーパラメータの初期値を指定する。
各パラメータが一様であるか多様であるかを決める。一様を仮定するなら、上のスカラーを作成する。多様な値を取ると仮定するなら、下のベクトルを作成する。
ここでは参考書に従って、トピック分布のパラメータ$\alpha$を多様に、単語分布のパラメータ$\beta$を一様とする。
・トピック集合
# 文書dの語彙vに割り当てられたトピック(z_dn)の集合 z_dn <- array(0, dim = c(D, V, max(N_dv)), dimnames = list(paste0("d=", 1:D), paste0("v=", 1:V), paste0("N_dv=", 1:max(N_dv))))
z_dvは、文書ごとの各単語に割り当てられたトピックの集合である。しかしここでは(参考書に逆らって)、単語レベル($n$)ではなく語彙レベル($v$)で扱い、$D$行$V$列の行列としたい。そこで、z_dvを$D$行$V$列の行列からなる配列とする。
トピックモデルでは、同じ単語であっても別のトピックが割り当てられる。そこで、配列の3次元目を出現回数とする。文書$d$の語彙$v$のトピックを3次元の方向に$N_{dv}$(出現回数)個格納されていくことになる。そのため、3次元方向の要素の数は出現回数の最大値max(N_dv)を用意しておく。
初回はどの文書にもトピックが割り当てられていない状態として、全ての要素を0としておく。出現回数以上の要素については0のままで推定が行われる。
・トピックごとの各カウント
# 文書dにおいてトピックkが割り当てられた単語数(N_dk)の集合 N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) # 文書全体でトピックkが割り当てられた語彙vの出現回数(N_kv)の集合 N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), paste0("v=", 1:V))) # 全文書でトピックkが割り当てられた単語数(N_k)のベクトル N_k <- rep(0, K)
N_dkは、文書$d$においてトピック$k$が割り当てられた単語数の集合で、$D$行$K$列の行列である。
N_kvは、語彙$v$においてトピック$k$が割り当てられた語数の集合で、$K$行$V$列の行列である。
N_kは、トピック$k$が割り当てられてられた総単語数のベクトルで、要素が$K$個である。
初回はどの文書にもトピックが割り当てられていないため、初期値は全て0である。
次からは、forループ内の処理である。
・ギブスサンプリング
・次ステップのカウントの初期化
## 新たに割り当られたトピックに関するカウントを初期化 new_N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) new_N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), paste0("v=", 1:V))) new_N_k <- rep(0, K)
new_N_dk、new_N_kv、new_N_kは、それぞれ現ステップでトピックを割り当られた単語に関するカウントを加算していく受け皿である。そのため、毎ステップの最初にカウントを0にリセットする。
次からは、各文書と各文書の語彙に対してループで処理を行う内容である。
for(d in 1:D)とfor(v in 1:V)に加えて、for(ndv in 1:N_dv[d, v])により各語彙の出現回数分繰り返し回す。それによって、単語レベルでトピックを割り当てることができる。ただし出現回数が0の語彙も含まれているため、if(N_dv[d, v] > 0)により、0なら以降の処理を行わないようにしておく。
・現ステップのカウント
# 現ステップの計算のためにカウントを移す tmp_N_dk <- N_dk tmp_N_kv <- N_kv tmp_N_k <- N_k if(z_dn[d, v, ndv] > 0) { # 初回を飛ばす処理 # 前ステップで文書dの語彙vに割り当てられたトピックを`k`に代入 k <- z_dn[d, v, ndv] # 文書dの語彙vの分のカウントを引く tmp_N_dk[d, k] <- N_dk[d, k] - 1 tmp_N_kv[k, v] <- N_kv[k, v] - 1 tmp_N_k[k] <- N_k[k] - 1 }
tmp_N_dk、tmp_N_kv、tmp_N_kは、それぞれ$N_{dk\backslash dn}$$N_{kv\backslash dn}$$N_{k\backslash dn}$のことである。これらの変数は、現ステップのサンプリング確率の計算に用いる。
これらは、文書$d$の$n$番目の単語(ここでは語彙$v$)を除いたカウントである。つまり、それぞれ該当する要素から1を引けばよい。
そのため、まず前ステップのカウントをそれぞれ移して、それぞれ該当する要素を添え字で指定して、そこから1を引く。ただし、初回については割り当てられたトピックがないためカウントを引く必要がない。そのため、初回にの処理に関してはif()を使って、処理を行わない。
・サンプリング確率の計算
for(k in 1:K) { ## 各トピック # サンプリング確率を計算 tmp_p_alpha <- tmp_N_dk[d, k] + alpha_k[k] tmp_p_beta_numer <- tmp_N_kv[k, v] + beta tmp_p_beta_denom <- tmp_N_k[k] + beta * V p[k] <- tmp_p_alpha * tmp_p_beta_numer / tmp_p_beta_denom }
サンプリング確率の計算は次の式によって行う。
ただし、ハイパーパラメータ$\alpha, \beta$を一様とする場合は
であり、また多様とする場合は
の式になる。
この計算をトピックごとに1つずつ行い、添え字を使って計算結果をpに代入していくため、最初に空のオブジェクトとしてpを作っておく。
・サンプリング
# サンプリング tmp_z_dn <- rmultinom(n = 1, size = 1:K, prob = p) z_dn[d, v, ndv] <- which(tmp_z_dn == 1)
上で求めた確率を基に、カテゴリ分布に従ってトピックを割り当てる。多項分布の乱数発生関数rmultinom()の引数にn = 1、size = 1を指定して試行回数を1回、サンプル数を1つとすることで、カテゴリ分布に従う乱数を発生させる。rmultinom()の結果は、サンプル確率を指定する引数probに渡す要素数の行、nに指定した試行回数の列のマトリクスで返ってくる。
この節の例では、$1, 2, \cdots, K$の行を持つ1列のマトリクスが返ってくる。要素は列ごとに、割り当てられたトピックの行が1でそれ以外は0となる。
出力された$K$行1列のマトリクスにwhich()を使い、要素が1の行番号を検索する。返ってきた値(行番号)がトピック番号に相当するので、それをz_dのd個目の要素に代入する。
・カウントの加算
# 新たに割り当てられたトピックを`k`に代入 k <- z_dn[d, v, ndv] # 文書dの語彙vの分のカウントを加える new_N_dk[d, k] <- new_N_dk[d, k] + 1 new_N_kv[k, v] <- new_N_kv[k, v] + 1 new_N_k[k] <- new_N_k[k] + 1
カウントを除いたときと同様に、現ステップで割り当てられたトピックについて該当する要素に加えていく。ループ処理の中で全ての単語分が加算される。
ここまでが、各文書・各語彙についてのループ処理の内容であった。次からは、この結果を基にパラメータを更新していく。
・カウントの更新
# トピック集合とカウントを更新 N_dk <- new_N_dk N_kv <- new_N_kv N_k <- new_N_k
全ての単語に関するカウントを集計できたので、その結果をそれぞれN_dk、N_kv、N_kに上書きする。
・ハイパーパラメータ$\alpha$の更新
# ハイパーパラメータ(alpha)の更新:一様 tmp_alpha_numer1 <- sum(digamma(N_dk + alpha)) # 分子 tmp_alpha_numer2 <- D * K * digamma(alpha) # 分子 tmp_alpha_denom1 <- K * sum(digamma(N_d + alpha * K)) # 分母 tmp_alpha_denom2 <- D * K * digamma(alpha * K) # 分母 alpha <- alpha * (tmp_alpha_numer1 - tmp_alpha_numer2) / (tmp_alpha_denom1 - tmp_alpha_denom2) # ハイパーパラメータ(alpha)の更新:多様 tmp_alpha_numer1 <- apply(digamma(t(N_dk) + alpha_k), 1, sum) # 分子 tmp_alpha_numer2 <- D * digamma(alpha_k) # 分子 tmp_alpha_denom1 <- sum(digamma(N_d + sum(alpha_k))) # 分母 tmp_alpha_denom2 <- D * digamma(sum(alpha_k)) # 分母 alpha_k <- alpha_k * (tmp_alpha_numer1 - tmp_alpha_numer2) / (tmp_alpha_denom1 - tmp_alpha_denom2)
$\alpha$の更新式(一様)は
である。また多様の場合は
である。
分かりやすくするために、各項を分けて計算した上で、最後にまとめて計算を行う。
・ハイパーパラメータ$\beta$の更新
# ハイパーパラメータ(beta)の更新:一様 tmp_beta_numer1 <- sum(digamma(N_kv + beta)) # 分子 tmp_beta_numer2 <- K * V * digamma(beta) # 分子 tmp_beta_denom1 <- V * sum(digamma(N_k + beta * V)) # 分母 tmp_beta_denom2 <- K * V * digamma(beta * V) # 分母 beta <- beta * (tmp_beta_numer1 - tmp_beta_numer2) / (tmp_beta_denom1 - tmp_beta_denom2) # ハイパーパラメータ(beta)の更新:多様 tmp_beta_numer1 <- apply(digamma(t(N_kv) + beta_v), 1, sum) # 分子 tmp_beta_numer2 <- K * digamma(beta_v) # 分子 tmp_beta_denom1 <- sum(digamma(N_k + sum(beta_v))) # 分母 tmp_beta_denom2 <- K * digamma(sum(beta_v)) # 分母 beta_v <- beta_v * (tmp_beta_numer1 - tmp_beta_numer2) / (tmp_beta_denom1 - tmp_beta_denom2)
$\beta$の更新式(一様)は
である。また多様の場合は
である。
こちらも同様に、各項分けて計算する。
・ハイパーパラメータの推定結果の確認
## トピック分布の推定結果の確認 # データフレームを作成 alpha_df <- data.frame(topic = as.factor(1:K), alpha = alpha_k) # 描画 ggplot(data = alpha_df, mapping = aes(x = topic, y = alpha, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 折れ線グラフ labs(title = "LDA:Gibbs Sampling") # タイトル

・パラメータ推定結果(平均値)の確認
## トピック分布(平均値)の確認 # データフレームを作成 theta_df <- data.frame(topic = as.factor(1:K), prob = alpha_k / sum(alpha_k)) # 描画 ggplot(data = theta_df, mapping = aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 折れ線グラフ labs(title = "LDA:Gibbs Sampling") # タイトル
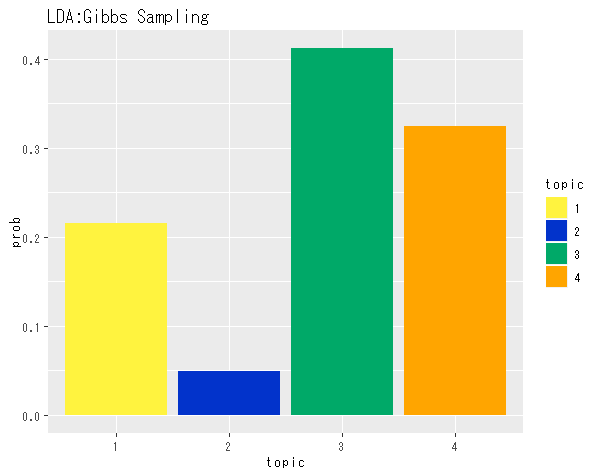
・推定推移の確認
・推移の記録
# 結果の確認用(初期値) trace_alpha <- as.matrix(alpha_k) trace_beta <- beta # 結果の確認用(更新後) trace_alpha <- cbind(trace_alpha, as.matrix(alpha_k)) trace_beta <- c(trace_beta, beta)
推移を確認するために、ハイパーパラメータを更新する度に記録しておく。
・トピック分布のパラメータ(多様)
## トピック分布のパラメータの推移の確認 # データフレームを作成 alpha_df_wide <- cbind(as.data.frame(t(trace_alpha)), as.factor(1:ncol(trace_alpha))) # 推定回数 # データフレームをlong型に変換 colnames(alpha_df_wide) <- c(1:K, "n") # key用の行名を付与 alpha_df_long <- gather(alpha_df_wide, key = "topic", value = "alpha", -n) # 変換 alpha_df_long$n <- alpha_df_long$n %>% as.numeric() # 描画 ggplot(data = alpha_df_long, mapping = aes(x = n, y = alpha, color = topic)) + # データ geom_line() + # 折れ線グラフ labs(title = "LDA:Gibbs Sampling") # タイトル

・単語分布のパラメータ(一様)
## 単語分布のパラメータの推移の確認 # データフレームを作成 beta_df <- data.frame(n = 1:length(trace_beta), # 推定回数 beta = trace_beta) # 描画 ggplot(data = beta_df, mapping = aes(x = n, y = beta)) + # データ geom_line() + # 折れ線グラフ labs(title = "LDA:Gibbs Sampling") # タイトル

取り得る値が多様の場合のコードは以下になる。
(クリックで展開)
# 結果の確認用(初期値) trace_beta <- as.matrix(beta_v) # 結果の確認用(更新後) trace_beta <- cbind(trace_beta, as.matrix(beta_v)) ## 単語分布のパラメータの推移の確認 # データフレームを作成 beta_df_wide <- cbind(as.data.frame(t(trace_beta)), as.factor(1:ncol(trace_beta))) # 推定回数 # データフレームをlong型に変換 colnames(beta_df_wide) <- c(1:V, "n") # key用の行名を付与 beta_df_long <- gather(beta_df_wide, key = "topic", value = "beta", -n) # 変換 beta_df_long$n <- beta_df_long$n %>% as.numeric() # 描画 ggplot(data = beta_df_long, mapping = aes(x = n, y = beta, color = topic)) + # データ geom_line(alpha = 0.5) + # 折れ線グラフ theme(legend.position = "none") + # 凡例 labs(title = "LDA:Gibbs Sampling") # タイトル

両方を一様とするの場合のコードは以下になる。
(クリックで展開)
# 結果の確認用(初期値) trace_alpha <- alpha trace_beta <- beta # 結果の確認用(更新後) trace_alpha <- c(trace_alpha, alpha) trace_beta <- c(trace_beta, beta) ## ハイパーパラメータの推移の確認 # データフレームを作成 ab_df_wide <- data.frame(n = seq_along(trace_alpha), # 推定回数 alpha = trace_alpha, beta = trace_beta) # データフレームをlong型に変換 ab_df_long <- gather(ab_df_wide, key = "parameter", value = "value", -n) # 描画 ggplot(data = ab_df_long, mapping = aes(x = n, y = value, color = parameter)) + # データ geom_line() + # 折れ線グラフ labs(title = "LDA:Gibbs Sampling") # タイトル

参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
この記事で、4章終了、青本の基本編完了です!やはりかなり難しかったり、思ったよりも自分でできたり、色々でした。
この記事のコードでは少し微妙な値になるので、まだどこかおかしなところがあるような気もしています…。
これにて一旦青本はお休みして、白本と緑のベイズの本で復習・確認をしていきます。その後、5章以降の応用編や論文を参考に実践編などに挑戦へと想定しています。
あとはR力も高めたいです。以降は基礎的な関数で組むことに意味もなくなりますし、理論と並行してRでできることも増やさないと実装できぬ。
という訳で最後まで読んでいただきありがとうございました。トピックモデルについてもRについてもその他全てにおいて、何かありましたらご指摘いただけると大変助かります。よろしくお願いします。
ではこの辺で!!
おしまいっ!!
令和元年8月7日:ハロー!プロジェクトの新グループ『BEYOOOOONDS』のメジャーデビュー日!
【次節の内容】
- スクラッチ実装編
トピックモデルに対する周辺化ギブスサンプリングをプログラムで確認します。
- 数式読解編
結合トピックモデルの生成モデルを数式で確認します。