【R】3.2.4：LDAの周辺化ギブスサンプリング【白トピックモデルのノート】

はじめに

　『トピックモデルによる統計的潜在意味解析』の学習時のメモです。本と併せて読んでください。

　この記事では、3.2.4項のLDAの周辺化ギブスサンプリングについて書いています。図3.2の疑似コードを基にR言語で実装していきます(未完)。

　プログラムからアルゴリズムの理解を目指します。できるだけ基本的な(直感的理解できる)関数を用いて組んでいきます。

【数理編】

www.anarchive-beta.com

【前節の内容】

www.anarchive-beta.com

【他の節一覧】

www.anarchive-beta.com

【この節の内容】

3.2.3 LDAのギブスサンプリング

　図3.2の疑似コードを参考にLDAに対する周辺化ギブスサンプリングを実装していきます。

# 利用パッケージ
library(tidyverse)

・簡易文書データ(クリックで展開)

## 簡易文書データ
# 文書数
M <- 10

# 語彙数
V <- 20

# 文書ごとの各語彙の出現回数
n_dv <- matrix(sample(0:10, M * V, replace = TRUE), M, V)

・パラメータの設定

　始めにパラメータ類の初期値を設定していきます。

# サンプリング回数を指定
S <- 500

# トピック数を指定
K <- 5

　サンプリング回数をS、トピックの数をKとします。

# 事前分布のパラメータを指定
alpha_k <- rep(2, K)
beta_v  <- rep(2, V)

　トピック分布のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \cdots, \alpha_K)$、単語分布のパラメータ$\boldsymbol{\beta} = (\beta_1, \cdots, \beta_V)$の値をそれぞれ指定します。どちらもディリクレ分布のパラメータなので、$\alpha_k > 0,\ \beta_v > 0$である必要があります。

　この例では値を一様に設定します。

# 潜在トピック集合の初期値
z_dvn <- array(0, dim = c(M, V, max(n_dv)))

# 各文書において各トピックが割り当てられた単語数の初期値
n_dk <- matrix(0, nrow = M, ncol = K)

# 全文書において各トピックが割り当てられた語彙ごとの単語数の初期値
n_kv <- matrix(0, nrow = K, ncol = V)

　潜在トピック$\boldsymbol{Z}$の初期値は0(どの単語にもトピックが割り当てられていない状態)とします。なので、各トピックに関する単語数$n_{d,k},\ n_{k,v}$についても初期値は0になります。

　語彙(ユニーク単語)ではなく単語(重複した語も別の語として扱う)ごとに潜在トピック$z_{d,i}$を割り当てます(同じ語に対して別のトピックとなることがあります)。しかし語彙ではなく単語だと、文書ごとの総単語数$n_d$が異なる(マトリクスで扱えない)ため扱いづらいです。そこで添字$i$を、$v$と$n$(1からmax(n_dv))に分けて3次元配列として扱うことにします。なので分かりやすいように変数名をz_dvnとします。

　それに伴い、疑似コードのfor i = 1,...,n_d doの処理を

for(v in 1:V) { ## (各語彙)
  if(n_dv[d, v] > 0) { ## (出現回数が0のときは行わない)
    for(n in 1:n_dv[d, v]) { ## (各単語)
      #z_dvn[d, v, n]のサンプリング
    }
  }
}

とします。
　よってz_dvn[d, v, n]の3次元方向について、各語彙の出現回数より大きい値は初期値0のままとなります。NAではなく0としておくと、後のn_dk, n_kvの計算が楽になります。

・周辺化ギブスサンプリング

　続いて推論部分の実装をしていきます。

・コード全体(クリックで展開)

# 推移の確認用
trace_alpha <- matrix(0, nrow = K, ncol = S + 1)
trace_beta <- matrix(0, nrow = V, ncol = S + 1)
# 初期値を代入
trace_alpha[, 1] <- alpha_k
trace_beta[, 1] <- beta_v

for(s in 1:S) { ## (イタレーション)
  
  # 動作確認用
  star_time <- Sys.time()
  
  for(d in 1:M) { ## (各文書)
    
    for(v in 1:V) { ## (各語彙)
      if(n_dv[d, v] > 0) { ## (出現回数が0のときは行わない)
        for(n in 1:n_dv[d, v]) { ## (各単語)
          
          # 更新した値を移す
          n_dk.di <- n_dk
          n_kv.di <- n_kv
          
          if(s > 1) { ## (初回以外)
            
            # d,i要素のトピック番号を取り出す
            k <- z_dvn[d, v, n]
            
            # d,i要素に関する値を除く
            n_dk.di[d, k] <- n_dk.di[d, k] - 1
            n_kv.di[k, v] <- n_kv.di[k, v] - 1
            
          }
          
          # 潜在トピックのサンプリング確率を計算:式(3.38)
          tmp_kv <- log(t(t(n_kv.di) + beta_v))
          term_beta <- exp(tmp_kv[, v] - apply(tmp_kv, 1, max)) / apply(exp(tmp_kv - apply(tmp_kv, 1, max)), 1, sum) # (アンダーフロー対策)
          tmp_k <- log(n_dk.di[d, ] + alpha_k)
          term_alpha <- exp(tmp_k - max(tmp_k)) / sum(exp(tmp_k - max(tmp_k))) # (アンダーフロー対策)
          tmp_q_z_k <- term_beta * term_alpha
          q_z_k <- tmp_q_z_k / sum(tmp_q_z_k) # 正規化
          
          # 潜在トピックを割り当てる
          res_z <- rmultinom(n = 1, size = 1, prob = q_z_k)
          z_dvn[d, v, n] <- which(res_z == 1)
          
        } ## (/各単語)
      }
    } ## (/各語彙)
  } ## (/各文書)
  
  # 割り当てられたトピックに関する単語数を更新
  for(k in 1:K) {
    n_dk[, k] <- apply(z_dvn == k, 1, sum)
    n_kv[k, ] <- apply(z_dvn == k, 2, sum)
  }
  
  # トピック分布のパラメータを更新:式(3.191)
  alpha_numer <- apply(digamma(t(n_dk) + alpha_k) - digamma(alpha_k), 1, sum)
  alpha_denom <- sum(digamma(apply(t(n_dk) + alpha_k, 2, sum)) - digamma(sum(alpha_k)))
  alpha_k <- alpha_k * alpha_numer / alpha_denom
  
  # 単語分布のパラメータを更新:式(3.192)
  beta_numer <- apply(digamma(t(n_kv) + beta_v) - digamma(beta_v), 1, sum)
  beta_denom <- sum(digamma(apply(t(n_kv) + beta_v, 2, sum)) - digamma(sum(beta_v)))
  beta_v <- beta_v * beta_numer / beta_denom
  
  # 更新値の推移の確認用に値を保存
  trace_alpha[, s + 1] <- alpha_k
  trace_beta[, s + 1]  <- beta_v
  
  # 動作確認
  #print(paste0(s, "th Sample...", round(Sys.time() - star_time, 3)))
}

・$z_{d,i}$のサンプリング

# 値を移す
n_dk.di <- n_dk
n_kv.di <- n_kv

if(z_dvn[d, v, n] > 0) { ## (初回以外)
  
  # トピック番号を取り出す
  k <- z_dvn[d, v, n]
  
  # d,i要素を除く
  n_dk.di[d, k] <- n_dk.di[d, k] - 1
  n_kv.di[k, v] <- n_kv.di[k, v] - 1

}

　前回のサンプリングで割り当てられた潜在トピックz_dvn[d, v, n]からトピック番号を取り出しkに代入します。それぞれ該当する箇所から1を引くことで、$n_{d,k}^{\backslash d,i},\ n_{k,v}^{\backslash d,i}$を作ります。

　ただしn_dk.di, n_kv.diの初期値は全て0であるため、初回はこの処理を行いません。

# 潜在トピックのサンプリング確率を計算:式(3.38)
tmp_kv <- log(t(t(n_kv.di) + beta_v))
term_beta <- exp(tmp_kv[, v] - apply(tmp_kv, 1, max)) / apply(exp(tmp_kv - apply(tmp_kv, 1, max)), 1, sum) # (アンダーフロー対策)
tmp_k <- log(n_dk.di[d, ] + alpha_k)
term_alpha <- exp(tmp_k - max(tmp_k)) / sum(exp(tmp_k - max(tmp_k))) # (アンダーフロー対策)
tmp_q_z_k <- term_beta * term_alpha
q_z_k <- tmp_q_z_k / sum(tmp_q_z_k) # 正規化

　語彙ごとに、式(3.38)の計算を行います。

$$ p(z_{d,i} = k | w_{d,i} = v, \boldsymbol{w}^{\backslash d,i}, \boldsymbol{z}^{\backslash d,i}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = \frac{ n_{k,v}^{\backslash d,i} + \beta_v }{ \sum_{v'=1}^V n_{k,v'}^{\backslash d,i} + \beta_{v'} } \frac{ n_{d,k}^{\backslash d,i} + \alpha_k }{ \sum_{k'=1}^K n_{d,k'}^{\backslash d,i} + \alpha_{k'} } \tag{3.38} $$

　ただしデータ数が増えると、各確率値が小さくなるためアンダーフローの可能性があります。そこで対数をとり、次のように計算します。

$$ \begin{aligned} \frac{\exp(x_i)}{\sum_{i} \exp(x_i)} &= \frac{ \exp(-a) \exp(x_i) }{ \exp(-a) \sum_{i} \exp(x_i) } \\ &= \frac{ \exp(x_i - a) }{ \sum_{i} \exp(x_i - a) } \end{aligned} $$

この$a$を$\boldsymbol{x}$の最大値とすることでアンダーフロー対策になります(これがLogSumExp？？)。

　この確率を基に潜在トピックをサンプリングします。

# 潜在トピックを割り当てる
res_z <- rmultinom(n = 1, size = 1, prob = q_z_k)
z_dvn[d, v, n] <- which(res_z == 1)

　多項分布に従う乱数を生成します。rmultinom()の引数は、1語(size)に1つのトピック(n)を割り当てるのでどちらも1を指定します。
　結果はK行1列のマトリクスで返ってくるので、which()を使って値が1となった行を抽出します。その行番号が割り当てられたトピック番号$k$となります。

　この処理を各単語に対して行います。

　更新した潜在トピック集合z_dvnを基に、n_dk, n_kvを更新します。

# 割り当てられたトピックに関する単語数を更新
for(k in 1:K) {
  n_dk[, k] <- apply(z_dvn == k, 1, sum)
  n_kv[k, ] <- apply(z_dvn == k, 2, sum)
}

　$n_{d,k},\ n_{k,v}$の定義式は

$$ \begin{aligned} n_{d,k} &= \sum_{i=1}^{n_d} \delta(z_{d,i} = k) \\ n_{k,v} &= \sum_{d=1}^M \sum_{i=1}^{n_d} \delta(w_{d,i} = v, z_{d,i} = k) \end{aligned} $$

です。
　n_dk[, k]は、z_dvn == kがTRUEとなる要素数を文書(d)ごとに計算します。
　同様にn_kv[k, ]は、z_dvn == kがTRUEとなる要素数を語彙(v)ごとに計算します。

　これを1からKまで順番に行います。(for()を使わずスマートに計算したい…)

　次にこの2つの統計量を使ってハイパーパラメータを更新します。また次のサンプリング確率の計算にも利用します。

・ハイパーパラメータの更新

# トピック分布のパラメータを更新:式(3.191)
alpha_numer <- apply(digamma(t(n_dk) + alpha_k) - digamma(alpha_k), 1, sum)
alpha_denom <- sum(digamma(apply(t(n_dk) + alpha_k, 2, sum)) - digamma(sum(alpha_k)))
alpha_k <- alpha_k * alpha_numer / alpha_denom

　3.6節の更新式(3.191)

$$ \alpha_k^{(s)} = \alpha_k^{(s-1)} \frac{ \sum_{d=1}^M \Bigl[ \Psi(\mathbb{E}[n_{d,k}] + \alpha_k^{(s-1)}) - \Psi(\alpha_k^{(s-1)}) \Bigr] }{ \sum_{d=1}^M \Bigl[ \Psi \Bigl( \sum_{k'=1}^K \mathbb{E}[n_{d,k'}] + \alpha_{k'}^{(s-1)} \Bigr) - \Psi \Bigl( \sum_{k'=1}^K \alpha_{k'}^{(s-1)} \Bigr) \Bigr] } \tag{3.191} $$

の計算を行い、ハイパーパラメータを更新します。

# 単語分布のパラメータを更新:式(3.192)
beta_numer <- apply(digamma(t(n_kv) + beta_v) - digamma(beta_v), 1, sum)
beta_denom <- sum(digamma(apply(t(n_kv) + beta_v, 2, sum)) - digamma(sum(beta_v)))
beta_v <- beta_v * beta_numer / beta_denom

　同様に、3.6節の更新式(3.191)

$$ \beta_v^{(s)} = \beta_v^{(s-1)} \frac{ \sum_{k=1}^K \Bigl[ \Psi(\mathbb{E}[n_{k,v}] + \beta_v^{(s-1)}) - \Psi(\beta_v^{(s-1)}) \Bigr] }{ \sum_{k=1}^K \Bigl[ \Psi \Bigl( \sum_{v'=1}^V \mathbb{E}[n_{k,v'}] + \beta_{v'}^{(s-1)} \Bigr) - \Psi \Bigl( \sum_{v'=1}^V \beta_{v'}^{(s-1)} \Bigr) \Bigr] } \tag{3.192} $$

の計算を行い、ハイパーパラメータを更新します。

・推定結果の確認

　ggplot2パッケージを利用して、推定結果を可視化しましょう。

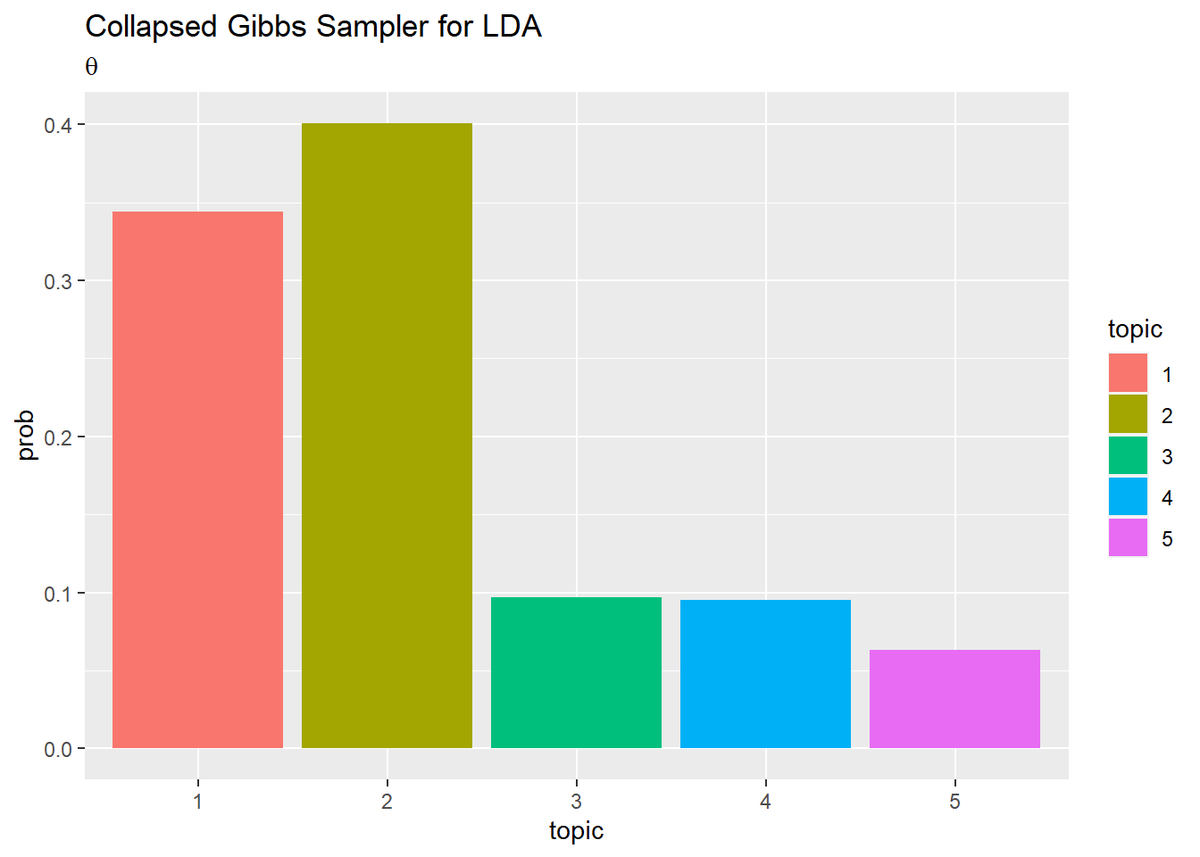
　ディリクレ分布の期待値(2.10)の計算を行いパラメータの期待値を作図します。

・トピック分布(クリックで展開)

## トピック分布(期待値)
# thetaの期待値を計算:式(2.10)
theta_k <- alpha_k / sum(alpha_k)

# 作図用のデータフレームを作成
theta_df <- tibble(
  prob = theta_k, 
  topic = as.factor(1:K) # トピック番号
)

# 作図
ggplot(theta_df, aes(x = topic, y = prob, fill = topic)) + 
  geom_bar(stat = "identity", position = "dodge") + # 棒グラフ
  labs(title = "Collapsed Gibbs Sampler for LDA", 
       subtitle = expression(theta)) # ラベル

トピック分布(期待値)

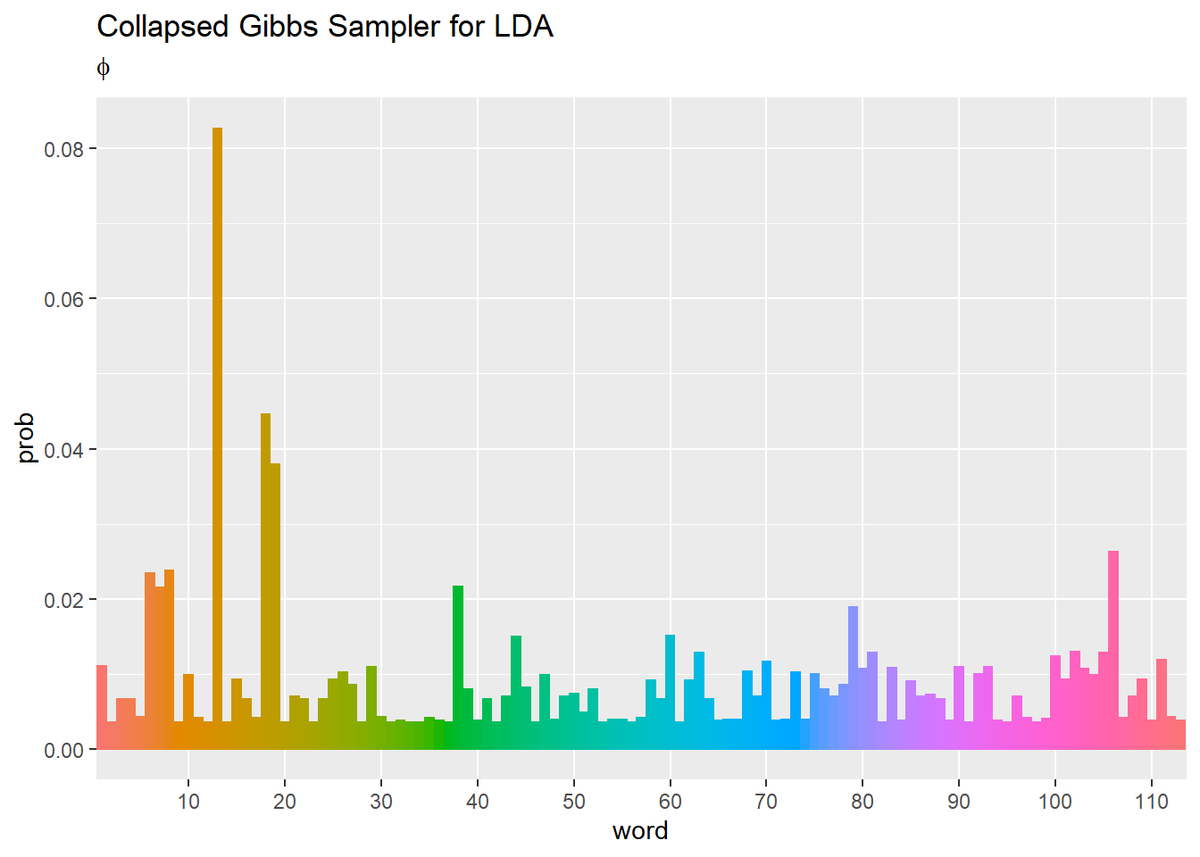
・単語分布(クリックで展開)

## 単語分布(期待値)
# phiの期待値を計算:式(2.10)
phi_v <- beta_v / sum(beta_v)

# 作図用のデータフレームを作成
phi_df <- tibble(
  prob = phi_v, 
  word = as.factor(1:V) # 語彙番号
)

# 作図
ggplot(phi_df, aes(x = word, y = prob, fill = word, color = word)) + 
  geom_bar(stat = "identity", position = "dodge") + # 棒グラフ
  scale_x_discrete(breaks = seq(0, V, by = 10)) + # x軸目盛
  theme(legend.position = "none") + # 凡例
  labs(title = "Collapsed Gibbs Sampler for LDA", 
       subtitle = expression(phi)) # ラベル

単語分布(期待値)

・更新値の推移の確認

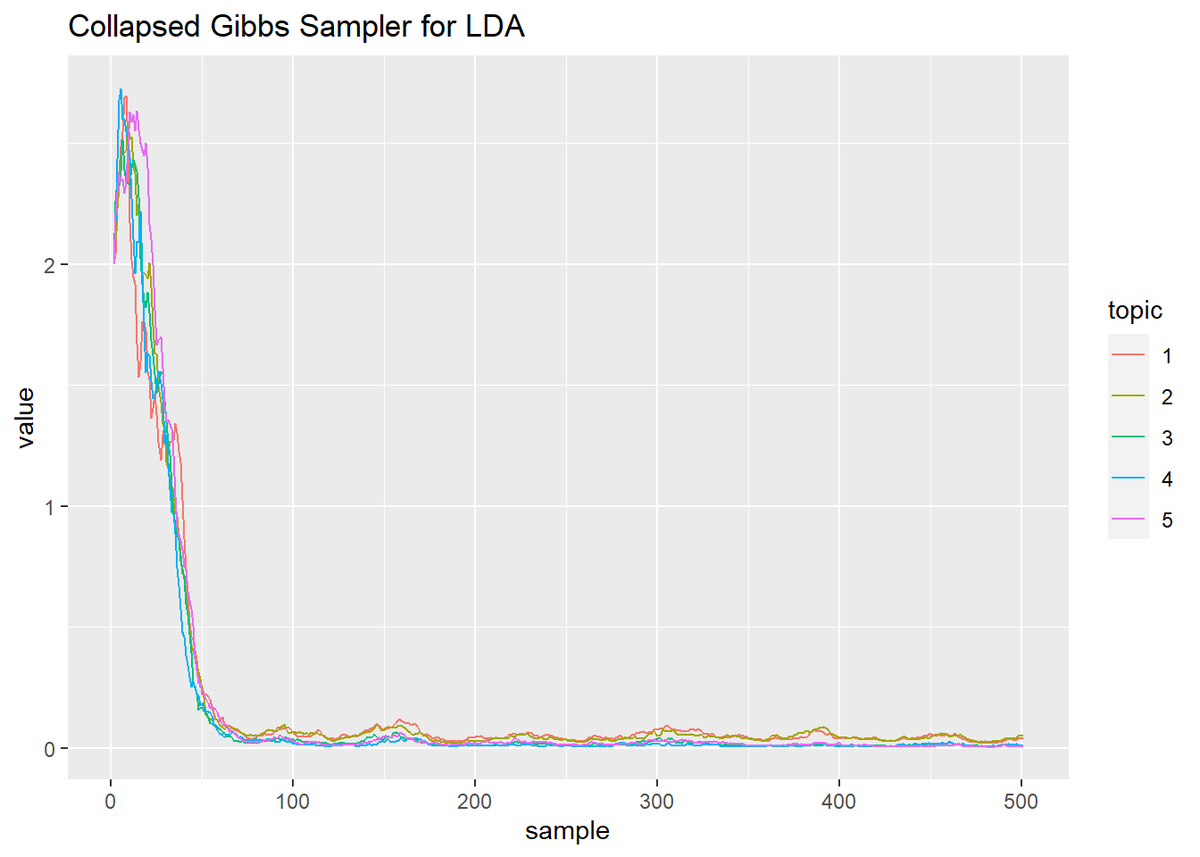
・トピック分布のパラメータ(クリックで展開)

## トピック分布のパラメータ
# 作図用のデータフレームを作成
trace_alpha_df_wide <- cbind(
  as.data.frame(trace_alpha), 
  topic = as.factor(1:K)
)

# データフレームをlong型に変換
trace_alpha_df_long <- pivot_longer(
  trace_alpha_df_wide, 
  cols = -topic, # 変換せずにそのまま残す現列名
  names_to = "sample", # 現列名を格納する新しい列の名前
  names_prefix = "V", # 現列名から取り除く文字列
  names_ptypes = list(sample = numeric()), # 現列名を要素とする際の型
  values_to = "value" # 現要素を格納する新しい列の名前
)

# 作図
ggplot(trace_alpha_df_long, aes(x = sample, y = value, color = topic)) + 
  geom_line() + # 折れ線グラフ
  labs(title = "Collapsed Gibbs Sampler for LDA") # ラベル

$\boldsymbol{\alpha}$の推移

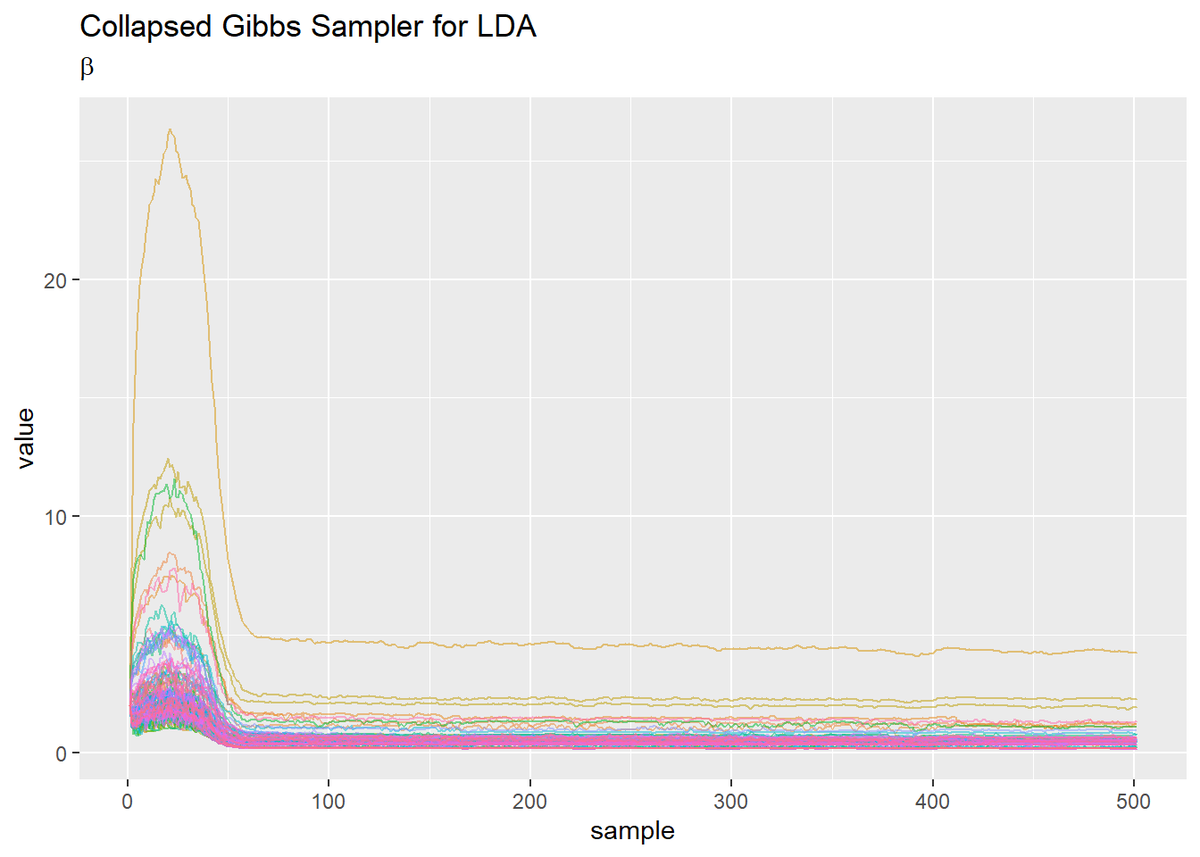
・単語分布のパラメータ(クリックで展開)

## 単語分布のパラメータ
# 作図用のデータフレームを作成
trace_beta_df_wide <- cbind(
  as.data.frame(trace_beta), 
  word = as.factor(1:V)
)

# データフレームをlong型に変換
trace_beta_df_long <- pivot_longer(
  trace_beta_df_wide, 
  cols = -word, # 変換せずにそのまま残す現列名
  names_to = "sample", # 現列名を格納する新しい列の名前
  names_prefix = "V", # 現列名から取り除く文字列
  names_ptypes = list(sample = numeric()), # 現列名を要素とする際の型
  values_to = "value" # 現要素を格納する新しい列の名前
)

# 作図
ggplot(trace_beta_df_long, aes(x = sample, y = value, color = word)) + 
  geom_line(alpha = 0.5) + # 折れ線グラフ
  theme(legend.position = "none") + # 凡例
  labs(title = "Collapsed Gibbs Sampler for LDA", 
       subtitle = expression(beta)) # ラベル

$\boldsymbol{\beta}$の推移

・gif画像を作成

・コード(クリックで展開)

　更新ごとの分布の変化をgif画像でみるためのコードです。gganimateパッケージを利用してgif画像を作成します。

# 利用パッケージ
library(gganimate)

## トピック分布(期待値)
# 作図用のデータフレームを作成
trace_theta_df_wide <- cbind(
  as.data.frame(t(trace_alpha) / apply(trace_alpha, 2, sum)), 
  sampling = 0:S
)

# データフレームをlong型に変換
trace_theta_df_long <- pivot_longer(
  trace_theta_df_wide, 
  cols = -sampling, # 変換せずにそのまま残す現列名
  names_to = "topic", # 現列名を格納する新しい列の名前
  names_prefix = "V", # 現列名から取り除く文字列
  names_ptypes = list(topic = factor()), # 現列名を要素とする際の型
  values_to = "prob" # 現要素を格納する新しい列の名前
)

# 作図
graph_theta <- ggplot(trace_theta_df_long, aes(topic, prob, fill = topic)) + 
  geom_bar(stat = "identity", position = "dodge") +  # 棒グラフ
  transition_manual(sampling) + # フレーム
  labs(title = "Gibbs sampler for LDA", 
       subtitle = "s={current_frame}") # ラベル

# gif画像を作成
animate(graph_theta, nframes = S + 1, fps = 10)

## 単語分布(期待値)
# 作図用のデータフレームを作成
trace_phi_df_wide <- cbind(
  as.data.frame(t(trace_beta) / apply(trace_beta, 2, sum)), 
  sampling = 0:S
)

# データフレームをlong型に変換
trace_phi_df_long <- pivot_longer(
  trace_phi_df_wide, 
  cols = -sampling, # 変換せずにそのまま残す現列名
  names_to = "word", # 現列名を格納する新しい列の名前
  names_prefix = "V", # 現列名から取り除く文字列
  names_ptypes = list(word = factor()), # 現列名を要素とする際の型
  values_to = "prob" # 現要素を格納する新しい列の名前
)

# 作図
graph_phi <- ggplot(trace_phi_df_long, aes(word, prob, fill = word, color = word)) + 
  geom_bar(stat = "identity", position = "dodge") + # 棒グラフ
  scale_x_discrete(breaks = seq(0, V, by = 10)) + # x軸目盛
  theme(legend.position = "none") + # 凡例
  transition_manual(sampling) + # フレーム
  labs(title = "Gibbs sampler for LDA", 
       subtitle = "s={current_frame}") # ラベル

# gif画像を作成
animate(graph_phi, nframes = S + 1, fps = 10)

　transition_manual()に時系列値の列を指定します。

2MB弱のgifファイルを上げられないんですが、、、ファイルサイズの上限は10MBとかじゃなかったでしたっけ。。。

参考文献

• 佐藤一誠『トピックモデルによる統計的潜在意味解析』(自然言語処理シリーズ 8)奥村学監修,コロナ社,2015年.

おわりに

【課題点メモ】

• 折れ線グラフでみる推移の仕方が2パターンに分かれる。
  1. どちらのパラメータも最初に山なりに推移し、その後0に漸近する。
  2. トピック分布は、どのトピックも増減しつつも上昇傾向で始まるが、徐々に値が小さくなっていくトピックが出てきてそのトピックが1語もサンプリングされなくなるとlog(0)となりエラー。また単語分布はほぼ線形に値が上がっていく。
• そもそも収束していない。

　まぁこんな感じです…完成度は如何ほど？

パターン2

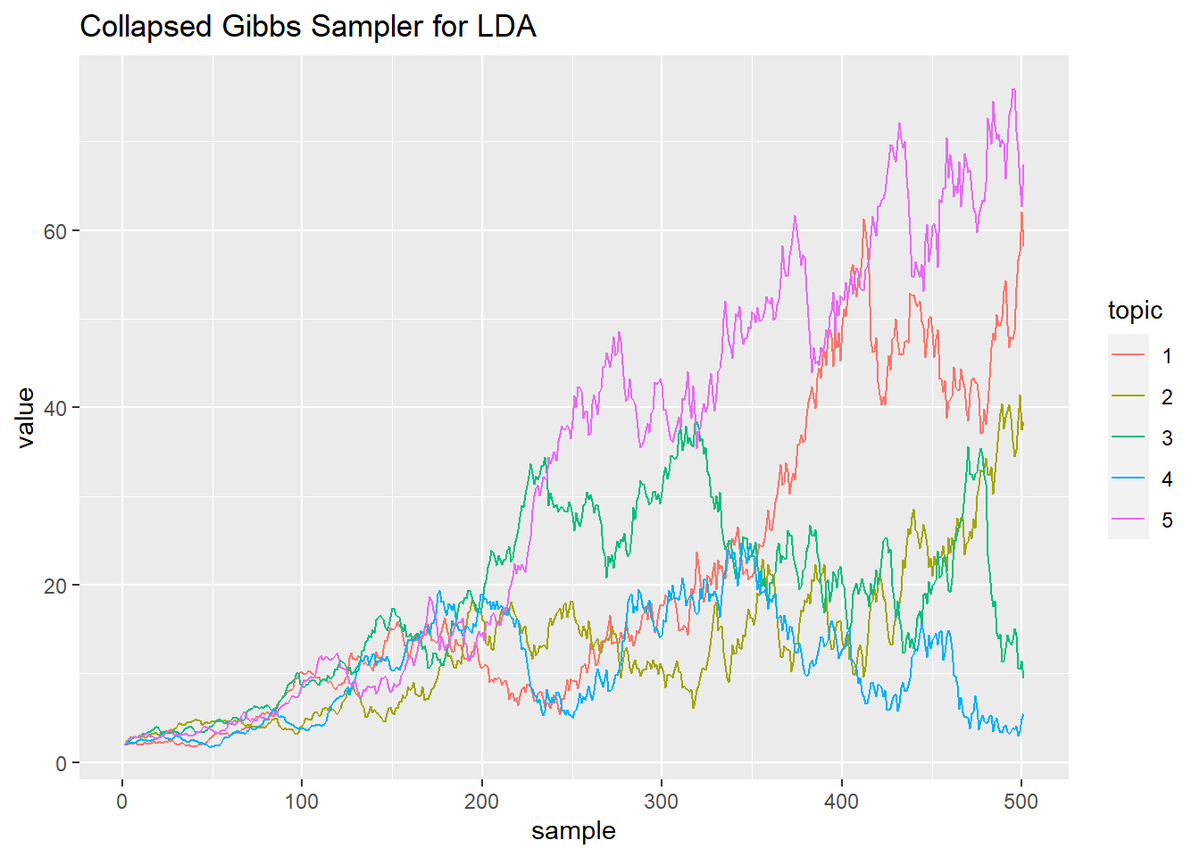
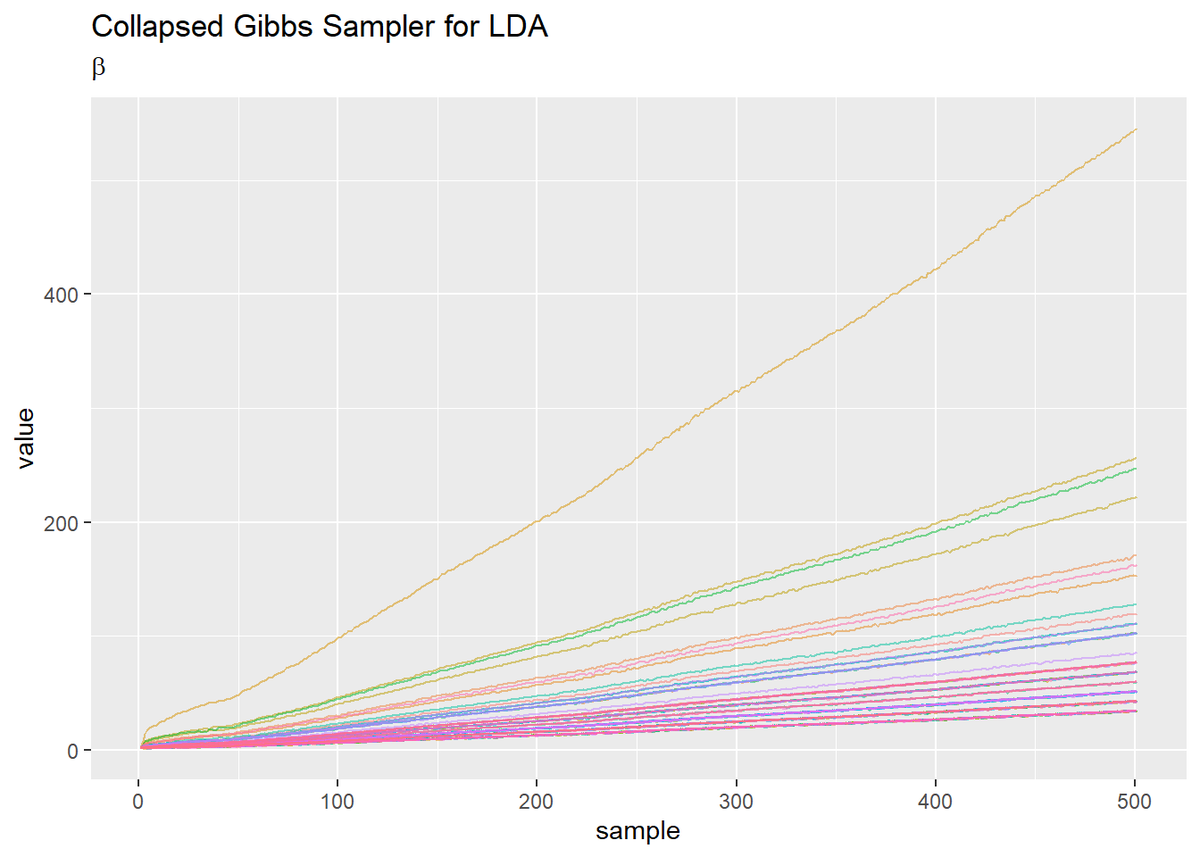
何に依存してそれぞれの形になるのか把握しておりませんが、こんな感じにもなります。青本を参考にほぼ同様のアルゴリズムを組んだときは、本文中の様になりました。はてさて。

　よく考えたら私はLDAに対するギブスサンプリングしか勉強しておらず、一般的なギブスサンプリングをやっておりません。1つ前のと合わせて実装にてこずったので、須山ベイズ4章をちょっとやってみたくらいです。
　という訳で素直にMCMCに入門します。早く本屋さん行きたい…

　明日の分はもう組み終わっているので、さらっと記事を書きたい！

【次節の内容】

www.anarchive-beta.com