はじめに
機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に理解の助けになったことや勉強会用レジュメのまとめです。
以前の記事「Chapter4.5:R言語でトピックモデルのギブスサンプリング【『トピックモデル』の勉強ノート】 - からっぽのしょこ」で、参考書のアルゴリズム4.3の疑似コードに従いR言語でギブスサンプリングのLDAを組みました。しかしそれは、推定過程を確認する意味もありパラメータの1要素ずつ計算・更新していきました。結果、鬼の5重ループで重いのなんのでした。
この記事は、それを3重ループにしたものです。
とは言うものの研究用とかではなく、あくまで勉強用です。基本的な関数のみで組みましたので、初級者でも理解できるはずです。(何より私が初級者ですので、、)
パラメータの更新式の導出などはこの記事「4.5:トピックモデルのギブスサンプリング【『トピックモデル』の勉強ノート】 - からっぽのしょこ」をご参照ください。この記事で説明していない部分に関しては、以前の記事の方をお読みください。
【他の節一覧】
【この節の内容】
・コード全体
# 利用パッケージ library(RMeCab) library(tidyverse)
・準備
・テキスト処理(クリックで展開)
## 抽出する単語の指定 # 品詞(大分類)を指定 PoS_1 <- "名詞|^動詞|形容詞" # 品詞(細分類)を指定 PoS_2 <- "一般|^自立" # 最低出現頻度を指定 Freq <- 5 # 抽出しない単語を指定 stop_words <- "[a-z]" # 形態素解析 mecab_df <- docDF("フォルダ名", type = 1) # テキストファイルの保存先を指定する # 文書dの語彙vの出現回数(N_dv)の集合 N_dv <- mecab_df %>% filter(grepl(PoS_1, POS1)) %>% # 指定した品詞(大分類)を取り出す filter(grepl(PoS_2, POS2)) %>% # 指定した品詞(細分類)を取り出す filter(!grepl(stop_words, TERM)) %>% # ストップワードを除く select(-c(TERM, POS1, POS2)) %>% # 数値列のみを残す filter(apply(., 1, sum) >= Freq) %>% # 指定した頻度以上の語彙を取り出す t() # 転置 # 確認用の行列名 dimnames(N_dv) <- list(paste0("d=", 1:nrow(N_dv)), # 行名 paste0("v=", 1:ncol(N_dv))) # 列名 # 文書dの単語数(N_d)のベクトル N_d <- apply(N_dv, 1, sum) # 行方向に和をとる # 文書数(D) D <- nrow(N_dv) # 総語彙数(V) V <- ncol(N_dv)
・パラメータの初期設定(クリックで展開)
# トピック数(K) K <- 4 # 値を指定する # ハイパーパラメータ(alpha, beta) alpha_k <- rep(2, K) # 値を指定する beta <- 2 # 値を指定する # 文書dの語彙vに割り当てられたトピック(z_dn)の集合 z_dn <- array(0, dim = c(D, V, max(N_dv)), dimnames = list(paste0("d=", 1:D), paste0("v=", 1:V), paste0("N_dv=", 1:max(N_dv)))) # 文書dにおいてトピックkが割り当てられた単語数(N_dk)の集合 N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) # 文書全体でトピックkが割り当てられた語彙vの出現回数(N_kv)の集合 N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), paste0("v=", 1:V))) # 全文書でトピックkが割り当てられた単語数(N_k)のベクトル N_k <- rep(0, K)
・Gibbs Sampling LDA
# 推定回数を指定 Iter <- 1000 # 受け皿 count_dvk <- array(0, dim = c(D, V, K)) # 結果の確認用 trace_alpha <- as.matrix(alpha_k) trace_beta <- beta trace_N_k <- as.matrix(N_k) # 推定 for(i in 1:Iter) { ## 新たに割り当られたトピックに関するカウントを初期化 new_N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) new_N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), paste0("v=", 1:V))) new_N_k <- rep(0, K) for(d in 1:D) { ## (文書) for(v in 1:V) { ## (各語彙) if(N_dv[d, v] > 0) { ## (出現回数:N_dv > 0のとき) # 現ステップの計算のためにカウントを移す tmp_N_dk <- N_dk tmp_N_kv <- N_kv tmp_N_k <- N_k if(z_dn[d, v, N_dv[d, v]] > 0) { # 初回を飛ばす処理 # 文書dの語彙vの分のカウントを引く tmp_N_dk[d, ] <- N_dk[d, ] - count_dvk[d, v, ] tmp_N_kv[, v] <- N_kv[, v] - count_dvk[d, v, ] tmp_N_k <- N_k - count_dvk[d, v, ] } # サンプリング確率を計算 tmp_p_alpha <- tmp_N_dk[d, ] + alpha_k tmp_p_beta_numer <- tmp_N_kv[, v] + beta tmp_p_beta_denom <- tmp_N_k + beta * V p <- tmp_p_alpha * tmp_p_beta_numer / tmp_p_beta_denom # サンプリング tmp_z_dn1 <- rmultinom(n = N_dv[d, v], size = 1, prob = p) tmp_z_dn2 <- which(tmp_z_dn1 == 1, arr.ind = TRUE) z_dn[d, v, 1:N_dv[d, v]] <- tmp_z_dn2[, "row"] # カウントを保存 count_dvk[d, v, ] <- apply(tmp_z_dn1, 1, sum) # 文書dの語彙vの分のカウントを加える new_N_dk[d, ] <- new_N_dk[d, ] + count_dvk[d, v, ] new_N_kv[, v] <- new_N_kv[, v] + count_dvk[d, v, ] new_N_k <- new_N_k + count_dvk[d, v, ] } ## (/出現回数:N_dv > 0のとき) } ## (/各語彙) } ## (/各文書) # トピック集合とカウントを更新 N_dk <- new_N_dk N_kv <- new_N_kv N_k <- new_N_k # ハイパーパラメータ(alpha)の更新 tmp_alpha_numer1 <- apply(digamma(t(N_dk) + alpha_k), 1, sum) # 分子 tmp_alpha_numer2 <- D * digamma(alpha_k) # 分子 tmp_alpha_denom1 <- sum(digamma(N_d + sum(alpha_k))) # 分母 tmp_alpha_denom2 <- D * digamma(sum(alpha_k)) # 分母 alpha_k <- alpha_k * (tmp_alpha_numer1 - tmp_alpha_numer2) / (tmp_alpha_denom1 - tmp_alpha_denom2) # ハイパーパラメータ(beta)の更新 tmp_beta_numer1 <- sum(digamma(N_kv + beta)) # 分子 tmp_beta_numer2 <- K * V * digamma(beta) # 分子 tmp_beta_denom1 <- V * sum(digamma(N_k + beta * V)) # 分母 tmp_beta_denom2 <- K * V * digamma(beta * V) # 分母 beta <- beta * (tmp_beta_numer1 - tmp_beta_numer2) / (tmp_beta_denom1 - tmp_beta_denom2) # 結果の確認用 trace_alpha <- cbind(trace_alpha, as.matrix(alpha_k)) trace_beta <- c(trace_beta, beta) trace_N_k <- cbind(trace_N_k, as.matrix(N_k)) }
・コードの解説
各文書の語彙ごとにパラメータ推定を行っていきます。
Rではベクトルとマトリクスとを計算するとき、ベクトルの各要素をマトリクスの1行1列目の要素から列方向に順番に対応させて計算していきます。つまり、ベクトルの要素の数とマトリクスの列の要素の数(行数)を一致させると、ベクトルの1つ目の要素をマトリクスの1行目の各要素に対応させることができます。なので、適宜転置して計算していきます。
・サンプリング確率の計算
# サンプリング確率を計算 tmp_p_alpha <- tmp_N_dk[d, ] + alpha_k tmp_p_beta_numer <- tmp_N_kv[, v] + beta tmp_p_beta_denom <- tmp_N_k + beta * V p <- tmp_p_alpha * tmp_p_beta_numer / tmp_p_beta_denom
サンプリング確率の計算式は
です。
全てK次元ベクトルかスカラーなので、そのまま計算します。
・サンプリング
続いて、求めた確率pを使ってトピックをサンプリングします。
# サンプリング tmp_z_dn1 <- rmultinom(n = N_dv[12, 7], size = 1, prob = p)
rmultinom()で多項分布に従いトピックを割り当てます。
引数n = N_dv[d, v]で各語彙の出現回数だけ試行します。語彙の出現回数1回(つまり各単語)ごとにトピックを1つ割り当てるので、size = 1を指定します。prob = pで先ほど求めた確率を利用できます。prob引数には比率を与えればよいため、確率計算をする際に正規化しませんでした。
結果はこのように返ってきます。
tmp_z_dn1 ## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] ## k=1 0 0 1 0 0 0 0 0 0 0 ## k=2 1 1 0 1 1 1 1 1 1 1 ## k=3 0 0 0 0 0 0 0 0 0 0 ## k=4 0 0 0 0 0 0 0 0 0 0
行が各トピック、列が各単語を意味します。各列(各単語)の1となっている行番号が割り当てられたトピック番号になります。
また、これを行方向に合計すると各トピックが割り当てられた単語数になるので、カウントの足し引きに利用します。
次は、割り当てられたトピックの情報を取り出します。
tmp_z_dn2 <- which(tmp_z_dn1 == 1, arr.ind = TRUE)
which()を使って、値が1である位置を調べます。引数にarr.ind = TRUEを指定すると、次のように返ってきます。
tmp_z_dn2 ## row col ## k=2 2 1 ## k=2 2 2 ## k=1 1 3 ## k=2 2 4 ## k=2 2 5 ## k=2 2 6 ## k=2 2 7 ## k=2 2 8 ## k=2 2 9 ## k=2 2 10
rowの列が該当した(値が1だった)行番号になります。つまり、この列が割り当てられたトピック番号のベクトルになるので、取り出してz_dnに代入します。
・トピック分布のパラメータの更新
# ハイパーパラメータ(alpha)の更新 tmp_alpha_numer1 <- apply(digamma(t(N_dk) + alpha_k), 1, sum) # 分子 tmp_alpha_numer2 <- D * digamma(alpha_k) # 分子 tmp_alpha_denom1 <- sum(digamma(N_d + sum(alpha_k))) # 分母 tmp_alpha_denom2 <- D * digamma(sum(alpha_k)) # 分母 alpha_k <- alpha_k * (tmp_alpha_numer1 - tmp_alpha_numer2) / (tmp_alpha_denom1 - tmp_alpha_denom2)
$\boldsymbol{\alpha}$の各要素の計算式は
です。
$N_{dk} + \alpha_k$の計算は、D行K列のマトリクスとK次元ベクトルの計算のため、N_dkを転置してから足します。
最終的に、分子の項はK次元ベクトル、分母の項はスカラーになるので、そのまま計算します。
・単語分布のパラメータの更新
# ハイパーパラメータ(beta)の更新 tmp_beta_numer1 <- sum(digamma(N_kv + beta)) # 分子 tmp_beta_numer2 <- K * V * digamma(beta) # 分子 tmp_beta_denom1 <- V * sum(digamma(N_k + beta * V)) # 分母 tmp_beta_denom2 <- K * V * digamma(beta * V) # 分母 beta <- beta * (tmp_beta_numer1 - tmp_beta_numer2) / (tmp_beta_denom1 - tmp_beta_denom2)
$\beta$の各要素の計算式は
です。
$\beta$は一様に推定するためスカラーです。ベクトル(N_k)やマトリクス(N_kv)との計算もそのまま行えます。
また、分母分子全ての項がスカラーになるため、こちらもそのまま計算できます。
・推定結果の確認
・作図用関数の作成(クリックで展開)
### トピック分布のパラメータの推移の確認 fn_plotTraceAlpha <- function(trace_alpha){ # データフレームを作成 trace_alpha_WideDF <- cbind(as.data.frame(t(trace_alpha)), iteration = 1:(Iter + 1)) # 推定回数 # データフレームをlong型に変換 trace_alpha_LongDF <- pivot_longer( trace_alpha_WideDF, cols = -iteration, names_to = "topic", names_prefix = "k=", names_ptypes = list(topic = factor()), values_to = "alpha" ) # 描画 ggplot(data = trace_alpha_LongDF, mapping = aes(x = iteration, y = alpha, color = topic)) + geom_line() + # 折れ線グラフ labs(title = "LDA_Gibbs Sampling:alpha") # タイトル } ### 単語分布のパラメータの推移の確認 fn_plotTraceBeta <- function(trace_beta){ # データフレームを作成 trace_beta_DF <- data.frame(beta = trace_beta, iteration = 1:(Iter + 1)) # 推定回数 # 描画 ggplot(data = trace_beta_DF, mapping = aes(x = iteration, y = beta)) + # データ geom_line(color = "#00A968") + # 折れ線グラフ labs(title = "LDA_Gibbs Sampling:beta") # タイトル }
何度も実行するのが面倒だっただけで、関数化することに深い意味はありません。
・描画
# トピック分布のパラメータの推移の確認 fn_plotTraceAlpha(trace_alpha)
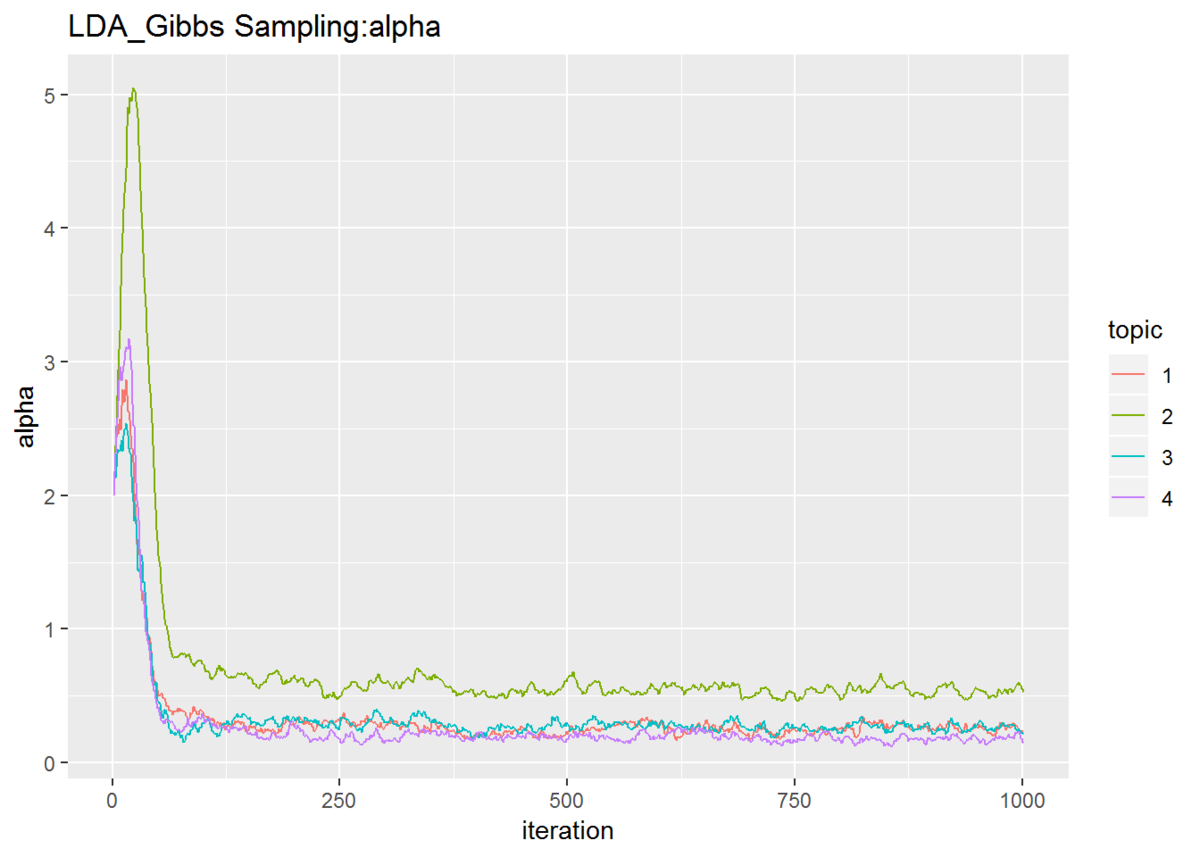
# 単語分布のパラメータの推移の確認 fn_plotTraceBeta(trace_beta)
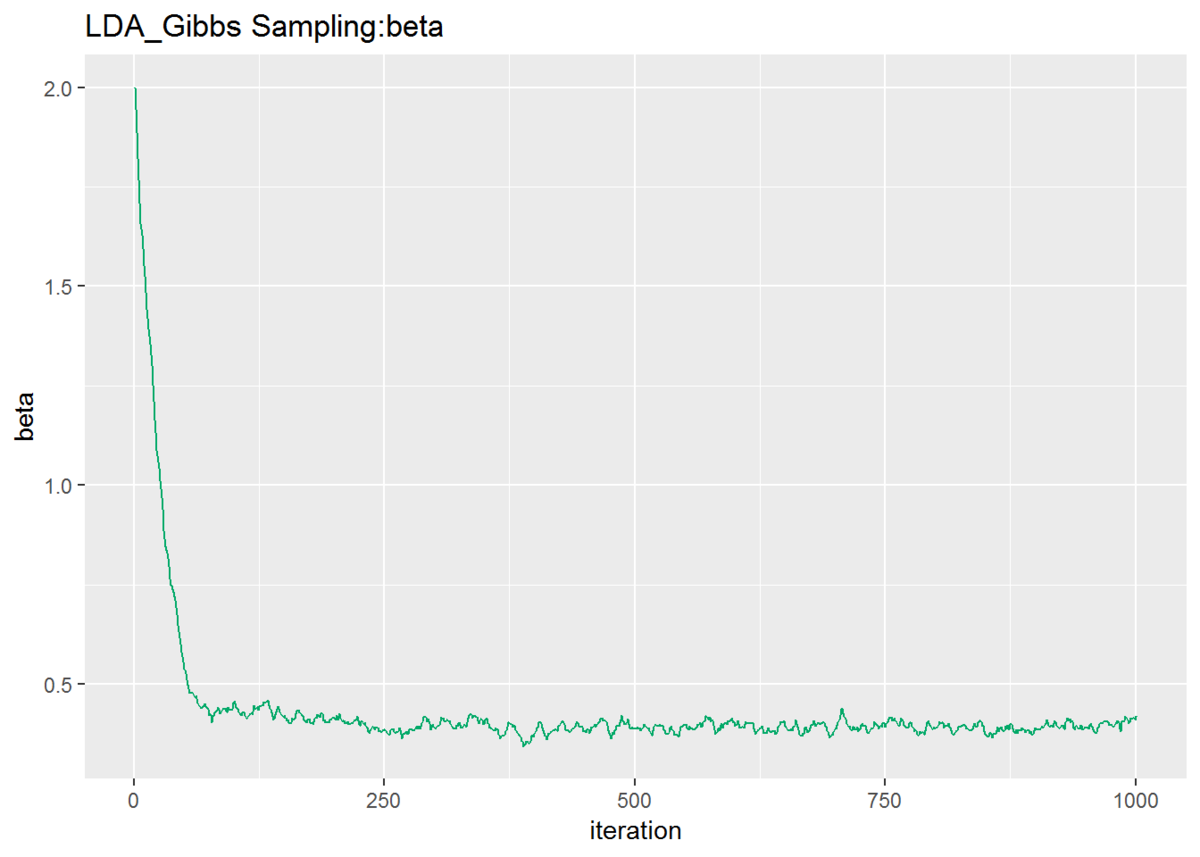
## トピック分布のパラメータの確認 # データフレームを作成 alpha_DF <- data.frame(topic = as.factor(1:K), alpha = alpha_k) # 描画 ggplot(data = alpha_DF, mapping = aes(x = topic, y = alpha, fill = topic)) + geom_bar(stat = "identity", position = "dodge") + # 折れ線グラフ labs(title = "LDA_Gibbs Sampling:alpha") # タイトル
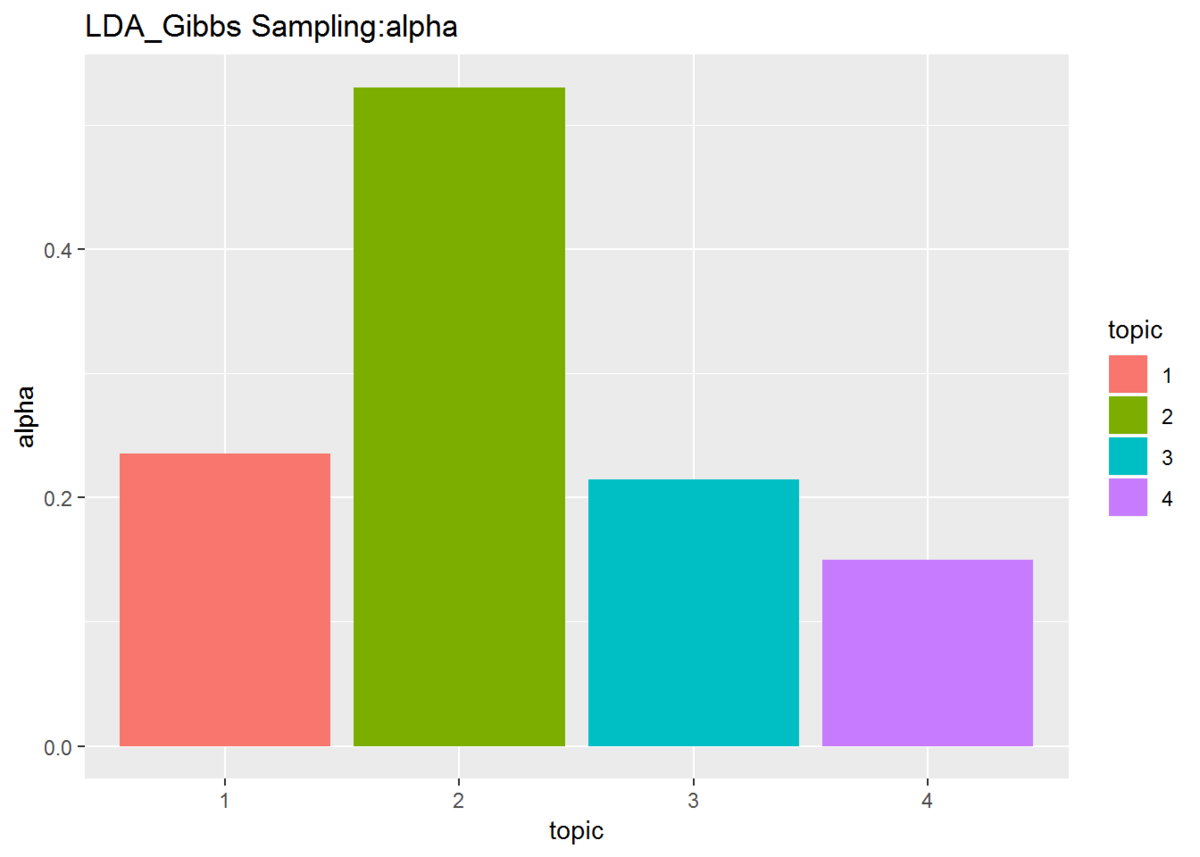
## トピック分布(平均値)の確認 # データフレームを作成 theta_DF <- data.frame(topic = as.factor(1:K), prob = alpha_k / sum(alpha_k)) # 描画 ggplot(data = theta_DF, mapping = aes(x = topic, y = prob, fill = topic)) + geom_bar(stat = "identity", position = "dodge") + # 折れ線グラフ labs(title = "LDA_Gibbs Sampling:theta") # タイトル
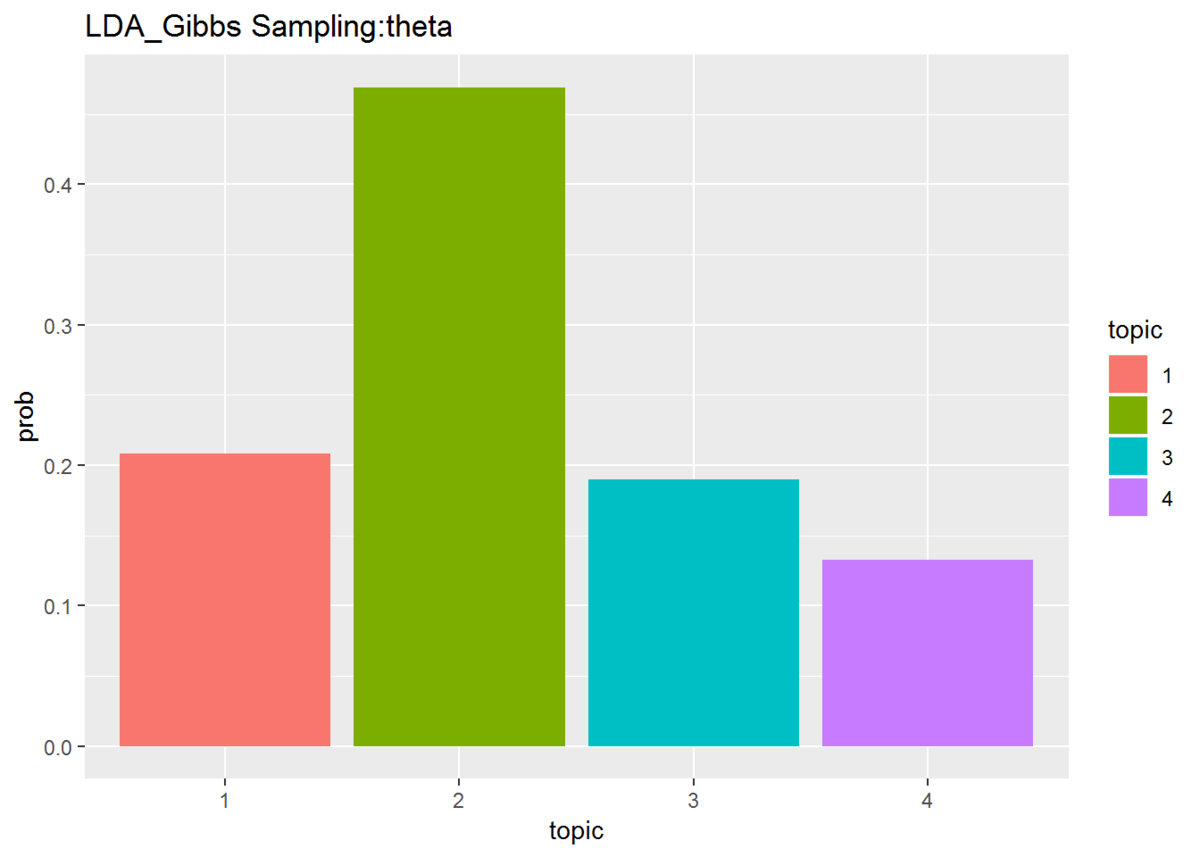
参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
もう少しなんとかなりそう…。特にwhich()の辺りとか。
その前に元記事の方も修正せねばな。
青本4章のトピックモデル3つについておまけ的な記事を書きました。さぁ次は5章へ!といきたいのですが、今は白本をやってるので、そちらの記事を書いていく予定です。あと緑のベイズ入門も進めたい。あと線形代数と微積の勉強も!こちらは記事にはならないでしょうが、今後の記事の内容に関わってきますゆえ。それとR4DSをですねぇ早急に・・・
最後まで読んでいただきありがとうございます。またよろしくお願いします。それでは!