はじめに

　『トピックモデル』(MLPシリーズ)の勉強会資料のまとめです。各種モデルやアルゴリズムを「数式」と「プログラム」を用いて解説します。
　本の補助として読んでください。

　この記事では、ユニグラムモデル(カテゴリモデル)の生成モデルをR言語でスクラッチ実装します。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

はじめに
2.2 ユニグラムモデルの生成モデルの実装
- 文書データの簡易生成
  - パラメータの設定
  - 頻度データの生成
    - 語順を記録する場合
    - 語順を記録しない場合
- データの可視化
参考書籍
おわりに

2.2 ユニグラムモデルの生成モデルの実装

　ユニグラムモデル(unigram model)の生成モデル(generative model)・生成過程(generative process)を実装して、簡易的な文書データ(トイデータ)を作成する。
　ユニグラムモデルの定義や記号については「2.2：ユニグラムモデルの生成モデルの導出【青トピックモデルのノート】 - からっぽのしょこ」、アルゴリズムについては図2.2を参照のこと。

　利用するパッケージを読み込む。

# 利用パッケージ
library(tidyverse)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要である。ただし、作図コードについてはパッケージ名を省略するので、ggplot2 を読み込む必要がある。
　また、ネイティブパイプ演算子 |> を使う。magrittrパッケージのパイプ演算子 %>% に置き換えられるが、その場合は magrittr を読み込む必要がある。

文書データの簡易生成

　まずは、ユニグラムモデルの生成モデルに従って、bag-of-words表現の文書データに対応する頻度データを作成する。

　真のパラメータや真の分布など本来は得られない情報についてはオブジェクト名に true を付けて表す。

パラメータの設定

　文書集合に関する値を設定する。

# 文書数を指定
D <- 10

# 語彙数を指定
V <- 6

　文書数 $D$ 、語彙(単語の種類)数 $V$ を指定する。

　単語分布のハイパーパラメータを設定する。

# 単語分布のハイパーパラメータを指定
true_beta   <- 1
true_beta_v <- rep(true_beta, times = V) # 一様な値の場合
#true_beta_v <- runif(n = V, min = 1, max = 2) # 多様な値の場合
true_beta_v

[1] 1 1 1 1 1 1

　 $V$ 個の値(ベクトル) $\boldsymbol{\beta} = (\beta_1, \cdots, \beta_V)$ を指定する。各値は0より大きい値 $\beta_v \gt 0$ を満たす必要がある。全て同じ値 $\beta_1 = \cdots = \beta_V = \beta$ とする場合は、1個の値(スカラ) $\beta$ で表す。

　単語分布のパラメータを設定する。

# 単語分布のパラメータを生成
#true_phi_v <- rep(1/V, times = V) # 一様な値の場合
true_phi_v <- MCMCpack::rdirichlet(n = 1, alpha = true_beta_v) |> # 多様な値の場合
  as.vector()
true_phi_v; sum(true_phi_v)

[1] 0.09510305 0.38607256 0.14895613 0.14595014 0.19758431 0.02633381
[1] 1

　単語分布(語彙分布)のパラメータ $\boldsymbol{\phi}$ を作成する。パラメータは $V$ 個の値(ベクトル) $\boldsymbol{\phi} = (\phi_1, \cdots, \phi_V)$ であり、各値は0から1の値 $0 \leq \phi_v \leq 1$ で、総和が1になる値 $\sum_{v=1}^V \phi_v = 1$ を満たす必要がある。
　ディリクレ分布の乱数は、rdirichlet() で生成できる。サンプルサイズの引数 n に文書数 1、パラメータの引数 alpha にハイパーパラメータ $\boldsymbol{\beta}$ を指定する。

頻度データの生成

　トピックモデルでは単語が出現した順番(語順)は考慮しないので、語順情報の有無によって2通り方法で頻度情報を作成する。どちらの方法でも同じ形式のオブジェクトを作成できる。

語順を記録する場合

　語彙の出現順と共に語彙ごとの出現頻度を作成する。こちらの方法では、ユニグラムモデルの生成過程をより再現するように処理している。

　設定したパラメータに従う文書データを作成する。

# 文書集合を初期化
w_lt <- list()

# 各文書の単語数を初期化
N_d <- rep(NA, times = D)

# 文書ごとの各語彙の単語数を初期化
N_dv <- matrix(0, nrow = D, ncol = V)

# 文書データを生成
for(d in 1:D) {
  
  # 単語数を生成
  N_d[d] <- sample(x = 10:20, size = 1) # 下限:上限を指定
  
  # 各単語の語彙を初期化
  w_n <- rep(NA, times = N_d[d]) # 単語集合
  
  for(n in 1:N_d[d]) { # 単語ごと
    
    # 語彙を生成
    onehot_v <- rmultinom(n = 1, size = 1, prob = true_phi_v) |> # (カテゴリ乱数)
      as.vector() # one-hot符号
    v <- which(onehot_v == 1) # 語彙番号
    
    # 語彙を割当
    w_n[n] <- v
    
    # 頻度をカウント
    N_dv[d, v] <- N_dv[d, v] + 1
  }
  
  # 単語集合を格納
  w_lt[[d]] <- w_n
  
  # 途中経過を表示
  print(paste0("document: ", d, ", words: ", N_d[d]))
}

[1] "document: 1, words: 20"
[1] "document: 2, words: 16"
[1] "document: 3, words: 16"
[1] "document: 4, words: 11"
[1] "document: 5, words: 19"
[1] "document: 6, words: 20"
[1] "document: 7, words: 17"
[1] "document: 8, words: 13"
[1] "document: 9, words: 18"
[1] "document: 10, words: 17"

個の文書について、順番に単語集合を生成していく。
- 文書 $d$ の単語数 $N_d$ をランダムに決める。この例では、下限数・上限数を指定して一様乱数を生成する。
- 個の単語について、順番に語彙を生成していく。
  - 単語分布(カテゴリ分布) $p(v | \boldsymbol{\phi})$ に従い、単語 $w_{dn}$ に $V$ 個の語彙 $\{1, \dots, V\}$ から語彙番号を割り当てる。
  - 生成した語彙に応じて出現回数 $N_{dv}$ をカウントする。

　文書間で単語数が異なる(マトリクスとして扱えない)ので、文書集合(単語集合の集合) $\mathbf{W} = \{\mathbf{w}_1, \cdots, \mathbf{w}_D\}$ をリストとして、単語集合 $\mathbf{w}_d = \{w_{d1}, \cdots, w_{dN_d}\}$ のベクトルを格納する。

　カテゴリ分布の乱数は、rmultinom() で生成できる。サンプルサイズの引数 n に 1、試行回数の引数 size に 1、パラメータの引数 prob に単語分布の $\boldsymbol{\phi}$ を指定する。
　one-hotベクトルが生成されるので、which() で値が 1 の要素番号を得る。
　または、sample() で直接番号を得られる。

　作成したデータを確認する。

# 観測データを確認
head(w_lt)
head(N_dv)

[[1]]
 [1] 2 2 4 2 5 2 2 4 6 2 2 3 5 3 3 1 1 2 2 3

[[2]]
 [1] 6 6 5 1 2 2 5 5 2 2 1 2 1 3 2 2

[[3]]
 [1] 2 4 2 2 2 3 2 2 3 5 1 5 4 2 5 2

[[4]]
 [1] 2 2 2 4 3 2 6 2 5 4 2

[[5]]
 [1] 3 3 5 1 3 5 4 2 2 4 5 5 3 2 4 1 1 2 6

[[6]]
 [1] 2 2 2 2 2 4 2 5 4 2 4 3 2 3 2 3 2 4 4 5

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    2    9    4    2    2    1
[2,]    3    7    1    0    3    2
[3,]    1    8    2    2    3    0
[4,]    0    6    1    2    1    1
[5,]    3    4    4    3    4    1
[6,]    0   10    3    5    2    0

　w_lt[[d]] が $\mathbf{w}_d$ 、w_lt[[d]][n] が $w_{dn}$ 、N_dv[d, v] が $N_{dv}$ に対応する。

語順を記録しない場合

　語順情報(文書集合)を作成せずに語彙ごとの出現頻度を作成する。こちらの方法では、より簡易的に処理している。

　設定したパラメータに従う文書データを作成する。

# 各文書の単語数を生成
N_d <- sample(x = 10:20, size = D, replace = TRUE) # 下限:上限を指定

# 文書ごとの各語彙の単語数を初期化
N_dv <- matrix(0, nrow = D, ncol = V)

# 文書データを生成
for(d in 1:D) { 
  
  # 各語彙の単語数を生成
  N_dv[d, ] <- rmultinom(n = 1, size = N_d[d], prob = true_phi_v) |> # (多項乱数)
    as.vector()
  
  # 途中経過を表示
  print(paste0("document: ", d, ", words: ", N_d[d]))
}

[1] "document: 1, words: 12"
[1] "document: 2, words: 14"
[1] "document: 3, words: 10"
[1] "document: 4, words: 10"
[1] "document: 5, words: 19"
[1] "document: 6, words: 16"
[1] "document: 7, words: 17"
[1] "document: 8, words: 14"
[1] "document: 9, words: 12"
[1] "document: 10, words: 17"

各文書の単語数 $(N_1, \cdots, N_D)$ をランダムに決める。この例では、下限数・上限数を指定して一様乱数を生成する。
個の文書について、順番に個分の語彙頻度を生成していく。
- 単語分布(カテゴリ分布) $p(v | \boldsymbol{\phi})$ に従い、 $V$ 個の語彙 $\{1, \dots, V\}$ ごとの出現回数 $(N_{d1}, \cdots, N_{dV})$ を生成する。

　多項分布の乱数は、rmultinom() で生成できる。サンプルサイズの引数 n に 1、試行回数の引数 size に $N_d$ 、パラメータの引数 prob に単語分布のパラメータ $\boldsymbol{\phi}$ を指定する。

　生成したデータを確認する。

# 観測データを確認
head(N_dv)

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    0    6    2    2    2    0
[2,]    1    7    3    1    2    0
[3,]    0    4    1    0    5    0
[4,]    1    7    2    0    0    0
[5,]    1    5    6    4    1    2
[6,]    0    5    5    3    3    0

　作図などで語順を使う場合は、ランダムに語順を決める。

# 文書集合を初期化
w_lt <- list()

# 文書ごとに単語集合を作成
for(d in 1:D) {
  
  # 語彙番号を作成
  v_vec <- mapply(
    FUN = \(v, n) {rep(v, times = n)}, # 語彙番号を複製
    1:V,      # 語彙番号
    N_dv[d, ] # 出現回数
  ) |> 
    unlist()
  
  # 語彙を割当
  w_n <- sample(x = v_vec, size = N_d[d], replace = FALSE) # 単語集合
  
  # 単語集合を格納
  w_lt[[d]] <- w_n
}
head(w_lt)

[[1]]
 [1] 2 5 2 2 2 3 4 2 3 4 2 5

[[2]]
 [1] 2 5 1 2 3 4 3 2 2 2 3 2 5 2

[[3]]
 [1] 2 5 5 5 5 3 2 2 5 2

[[4]]
 [1] 2 2 3 2 2 3 1 2 2 2

[[5]]
 [1] 3 4 6 2 2 2 3 1 3 3 5 6 2 2 4 4 3 4 3

[[6]]
 [1] 4 3 4 2 3 5 2 5 3 5 3 3 2 2 2 4

　mapply() を使って 1 から V の語彙番号を出現回数 N_dv[d, ] に応じてそれぞれ複製する。リストが出力されるので unlist() でベクトルに変換する。
　N_d[d] 個の語彙番号を sample() でランダムに入れ替えて単語集合のベクトルとする。
　文書ごとに単語集合のベクトルを作成して、文書集合のリストに格納していく。

　各種推論アルゴリズムでは、文書集合 $\mathbf{W}$ から得られる語彙頻度データ $(N_{11}, \cdots, N_{DV})$ のみを用いてパラメータ類を推定する。

データの可視化

　次は、生成した真の分布や文書データのグラフを作成する。

データの集計

　文書や語彙に関する単語数を集計する。

# 各文書の単語数を取得
N_d <- rowSums(N_dv)

# 各語彙の単語数を取得
N_v <- colSums(N_dv)
N_d; N_v

 [1] 12 14 10 10 19 16 17 14 12 17
[1] 15 53 30 18 19  6

　各文書の単語数 $(N_1, \cdots, N_D)$ 、 $N_d = \sum_{v=1}^V N_{dv}$ は N_dv の行ごとの和、各語彙の単語数 $(N_1, \cdots, N_V)$ 、 $N_v = \sum_{d=1}^D N_{dv}$ は N_dv の列ごとの和に対応する。

　文書集合に関する値を集計する。

# 文書数を取得
D <- nrow(N_dv)
D <- length(N_d)

# 語彙数を取得
V <- ncol(N_dv)
V <- length(N_v)

# 全文書の単語数を取得
N <- sum(N_dv)
N <- sum(N_d)
N <- sum(N_v)
D; V; N

[1] 10
[1] 6
[1] 141

　文書数 $D$ は N_dv の行数または N_d の要素数、語彙数 $V$ は N_dv の列数または N_d の要素数に対応する。
　全文書の単語数(総単語数) $N = \sum_{d=1}^D \sum_{v=1}^V N_{dv}$ は N_dv, N_d, N_v それぞれの全ての要素の和に対応する。

真の分布の図

　真の分布(パラメータ)をグラフで確認する。

単語分布

　単語分布の描画用のデータフレームを作成する。

# 単語分布を格納
true_phi_df <- tibble::tibble(
  v    = 1:V,       # 語彙番号
  prob = true_phi_v # 生成確率
)
true_phi_df

# A tibble: 6 × 2
      v   prob
  <int>  <dbl>
1     1 0.0951
2     2 0.386 
3     3 0.149 
4     4 0.146 
5     5 0.198 
6     6 0.0263

　語彙番号 $v$ とパラメータ $\phi_v$ を格納する。

　単語分布のグラフを作成する。

# ラベル用の文字列を作成
param_label <- paste0(
  "beta == ", true_beta
) # 一様な値の場合
param_label <- paste0(
  "beta == (list(", paste0(true_beta_v, collapse = ", "), "))"
) # 多様な値の場合

# 単語分布を作図
ggplot() + 
  geom_bar(data = true_phi_df, 
           mapping = aes(x = v, y = prob, fill = factor(v)), stat = "identity") + # 確率
  guides(fill = "none") + # 凡例の体裁
  labs(title = "word distribution (truth)", 
       subtitle = parse(text = param_label), 
       x = expression(vocabulary ~ (v)), 
       y = expression(probability ~ (phi[v])))

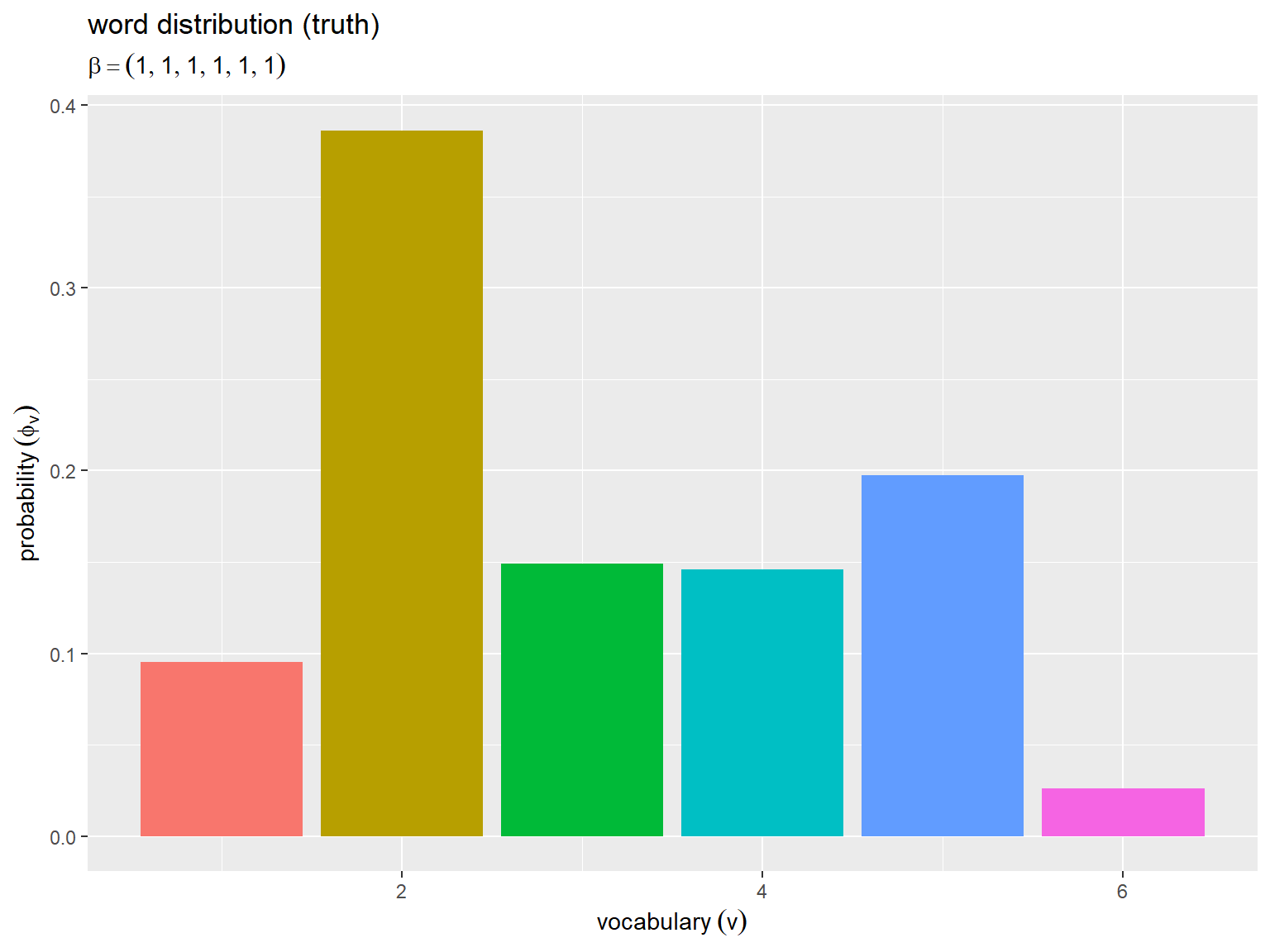
　横軸は語彙番号 $v$ 、縦軸は各語彙の出現確率 $\phi_v$ を表す。
　以降の図も含めて、語彙ごとにバーを色付けしている。

文書データの図

　文書集合(頻度データ)をグラフで確認する。

各文書における各語彙の単語数

　文書ごとの語彙頻度の描画用のデータフレームを作成する。

# 文書ごと語彙頻度を格納
Ndv_df <- N_dv |> 
  tibble::as_tibble(.name_repair = ~paste0("V", 1:V)) |> # 語彙番号の列名を設定
  tibble::add_column(
    d = 1:D # 文書番号
  ) |> 
  tidyr::pivot_longer(
    cols         = !d, 
    names_to     = "v", # 列名を語彙番号に変換
    names_prefix = "V", 
    names_transform = list(v = as.numeric), 
    values_to    = "freq" # 語彙頻度を1列に結合
  )
Ndv_df

# A tibble: 60 × 3
       d     v  freq
   <int> <dbl> <dbl>
 1     1     1     0
 2     1     2     6
 3     1     3     2
 4     1     4     2
 5     1     5     2
 6     1     6     0
 7     2     1     1
 8     2     2     7
 9     2     3     3
10     2     4     1
# ℹ 50 more rows

　文書ごとの語彙頻度データ N_dv をデータフレームに変換して、文書番号 $d$ と語彙番号 $v$ と単語数 $N_{dv}$ を格納する。

　文書ごとの単語数の描画用のデータフレームを作成する。

# 各文書の単語数を格納
Nd_df <- tibble::tibble(
  d    = 1:D, # 文書番号
  freq = N_d, # 単語数
  label = paste("N[d] ==", freq)
)
Nd_df

# A tibble: 10 × 3
       d  freq label     
   <int> <dbl> <chr>     
 1     1    12 N[d] == 12
 2     2    14 N[d] == 14
 3     3    10 N[d] == 10
 4     4    10 N[d] == 10
 5     5    19 N[d] == 19
 6     6    16 N[d] == 16
 7     7    17 N[d] == 17
 8     8    14 N[d] == 14
 9     9    12 N[d] == 12
10    10    17 N[d] == 17

　文書番号 $d$ と単語数 $N_d$ を格納する。また、単語数ラベル用の文字列を作成する。

　文書ごとの語彙頻度のグラフを作成する。

# ラベル用の文字列を作成
doc_label <- paste0(
  "list(", 
  "D == ", D, ", ", 
  "V == ", V, ", ", 
  "N == ", N, 
  ")"
)

# 文書ごとの語彙頻度を作図
ggplot() + 
  geom_bar(data = Ndv_df, 
           mapping = aes(x = v, y = freq, fill = factor(v)), stat = "identity") + # 頻度
  geom_label(data = Nd_df, 
             mapping = aes(x = -Inf, y = Inf, label = label), parse = TRUE, 
             hjust = 0, vjust = 1, alpha = 0.5) + # 単語数
  facet_wrap(d ~ ., labeller = label_bquote(document ~ (d): .(d))) + # 文書ごとに分割
  guides(fill = "none") + # 凡例の体裁
  labs(title = "document data", 
       subtitle = parse(text = doc_label), 
       x = expression(vocabulary ~ (v)), 
       y = expression(frequency ~ (N[dv])))

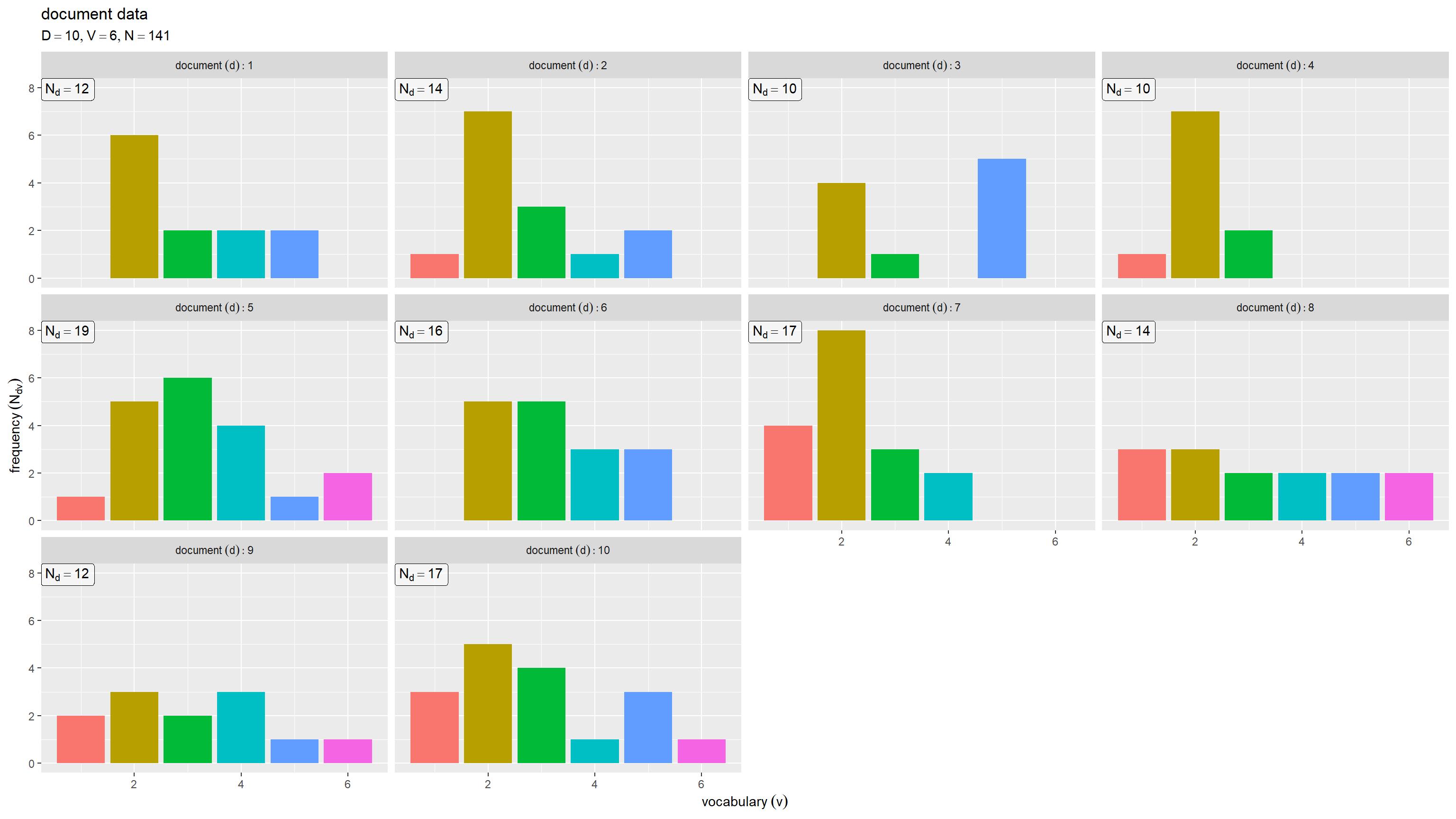
　横軸は語彙番号 $v$ 、縦軸は文書ごとの各語彙の出現回数 $N_{dv}$ を表す。文書ごとにグラフを縦横に並べている。
　各文書の単語数 $N_d$ が増えるとそれぞれ単語分布の形状に近付く。

各文書の単語数

　文書ごとの単語数のグラフを作成する。

# 各文書の単語数を作図
ggplot() + 
  geom_bar(data = Nd_df, 
           mapping = aes(x = d, y = freq), stat = "identity") + # 頻度
  labs(title = "document data", 
       subtitle = parse(text = doc_label), 
       x = expression(vocabulary ~ (d)), 
       y = expression(frequency ~ (N[d])))

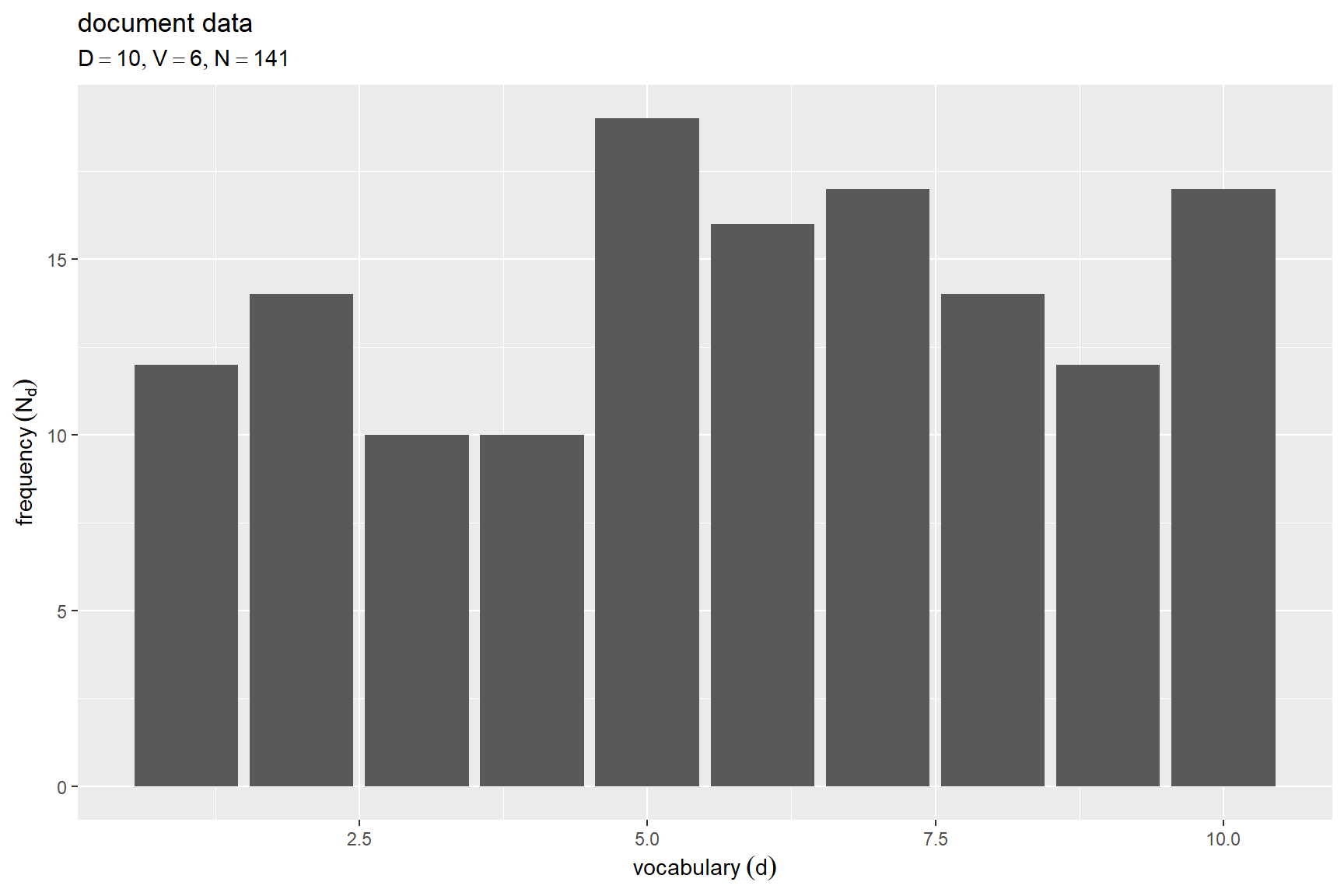
　横軸は文書番号 $d$ 、縦軸は各文書の単語数 $N_d$ を表す。
　この例では、一様分布に従い設定している。

全文書における各語彙の単語数

　全文書での語彙頻度の描画用のデータフレームを作成する。

# 全文書の語彙頻度を格納
Nv_df <- Ndv_df |> 
  dplyr::reframe(
    freq = sum(freq), .by = v, # 各語彙の単語数を集計
  )
Nv_df

# A tibble: 6 × 2
      v  freq
  <dbl> <dbl>
1     1    15
2     2    53
3     3    30
4     4    18
5     5    19
6     6     6

　語彙番号 $v$ と単語数 $N_v$ を格納する。

　全文書での語彙頻度をグラフで確認する。

# 全文書の語彙頻度を作図
ggplot() + 
  geom_bar(data = Nv_df, 
           mapping = aes(x = v, y = freq, fill = factor(v)), stat = "identity") + # 頻度
  guides(fill = "none") + # 図の体裁
  labs(title = "document data", 
       subtitle = parse(text = doc_label), 
       x = expression(vocabulary ~ (v)), 
       y = expression(frequency ~ (N[v])))

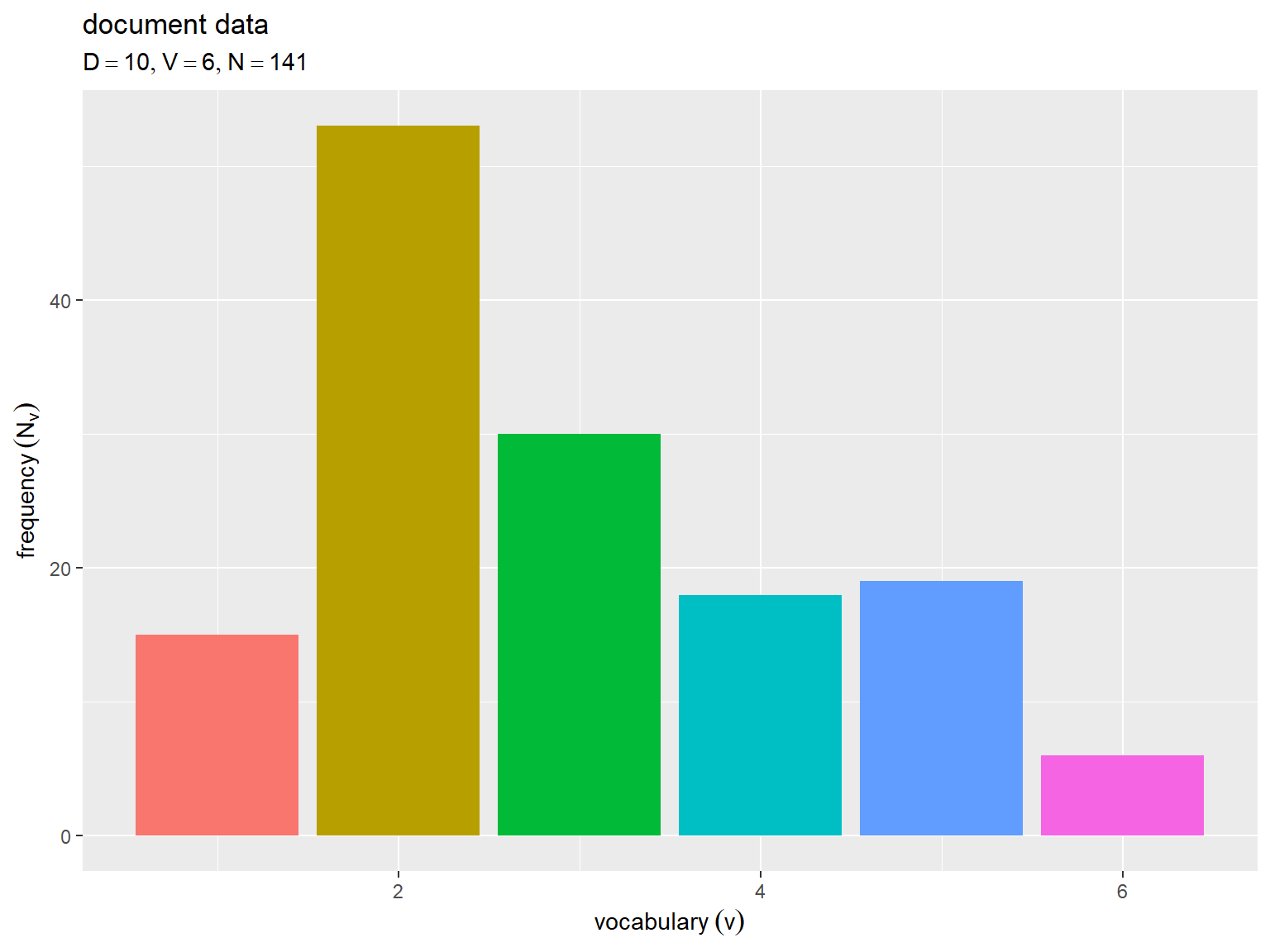
　横軸は語彙番号 $v$ 、縦軸は全文書での各語彙の出現回数 $N_v$ を表す。
　全文書での単語数 $N$ が増えると単語分布の形状に近付く。

　この記事では、ユニグラムモデルの生成モデルを実装して、各種推論アルゴリズムに用いる人工データを作成した。次の記事からは、3つの推論アルゴリズムを確認していく。

参考書籍

岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社

おわりに

　一言で説明するならば「歪んだサイコロを振った結果です」で済む内容を長々と書きました。1記事分の内容にするために無理くり工程を増やしているところもなくはないです。
　が、章が進むとトイデータを作るだけでもややこしくなり、推論パートの3記事で毎度説明するのも(読むのも)大変だし流れも悪くなるしなので、独立した記事にする必要が出てきました。だったら全体の構成上、2章の段階から別記事化しておこうと4周目にて判断しました。
　で、記事を独立させるなら、簡易版(使う用)とアルゴリズムに忠実版(理解用)の2パターン用意しようと書き始めたら結構なボリュームになりました。一番シンプルなモデルでこの文量ならこの先どうなることでしょう。

　投稿日の5月24日はこぶしの日ということで、こぶしファクトリーの曲をどうぞ♪

　こぶし(花)は3月~4月に咲くので、こぶし(グループ)の日という認識です。花はなくともこぶし(植物)はいつだってこぶしですけどね。
　私はインドアな人間ですが毎年3月頃になるとこぶしの花を見にお出かけするくらい好きな花でもあり、こぶしのライブを観に行くくらい好きなグループでもあります。

【次節の内容】

数式読解編

　ユニグラムモデルに対する最尤推定を数式で確認します。

www.anarchive-beta.com

スクラッチ実装編

　ユニグラムモデルに対する最尤推定をプログラムで確認します。

www.anarchive-beta.com

　混合ユニグラムモデルに対する生成モデルをプログラムで確認します。

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【R】2.2：ユニグラムモデルの生成モデルの実装【青トピックモデルのノート】

はじめに

2.2 ユニグラムモデルの生成モデルの実装

文書データの簡易生成

パラメータの設定

頻度データの生成

語順を記録する場合

語順を記録しない場合

データの可視化

データの集計

真の分布の図

単語分布

文書データの図

各文書における各語彙の単語数

各文書の単語数

全文書における各語彙の単語数

参考書籍

おわりに