はじめに
機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に自分の理解の助けになったことや勉強会資料のまとめです。トピックモデルの各種アルゴリズムを「数式」と「プログラム」から理解することを目指します。
この記事は、3.3節「EMアルゴリズム」の内容です。
EMアルゴリズを用いた最尤推定による混合ユニグラムモデルにおけるパラメータ推定を実装します。
【数式編】
【他の節一覧】
【この節の内容】
3.3 EMアルゴリズム:ループなし版
混合ユニグラムモデル(混合カテゴリ分布)に対するEMアルゴリズムを用いた最尤推定を実装する。
「【R】3.3:混合ユニグラムモデルの最尤推定(EMアルゴリズム)の実装【『トピックモデル』の勉強ノート】 - からっぽのしょこ」では、アルゴリズム3.1を参考にして、3重のループを使って実装した。この記事では、行列計算を使って、ループを使わずに実装する。
生成モデルの設定と文書データの生成、分布の可視化については「ループあり版」を参照のこと。
利用するパッケージを読み込む。
# 利用パッケージ library(tidyverse) library(gganimate) library(gtools)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はない。ただし、作図コードに関してはパッケージ名を省略するので、ggplot2を読み込む必要がある。
また、magrittrパッケージのパイプ演算子%>%ではなく、ネイティブパイプ演算子|>を使う。%>%に置き換えても処理できるが、その場合はmagrittrを読み込む必要がある。
文書データの簡易生成
人工的に生成した次の文書データ(bag-of-words)を利用する。
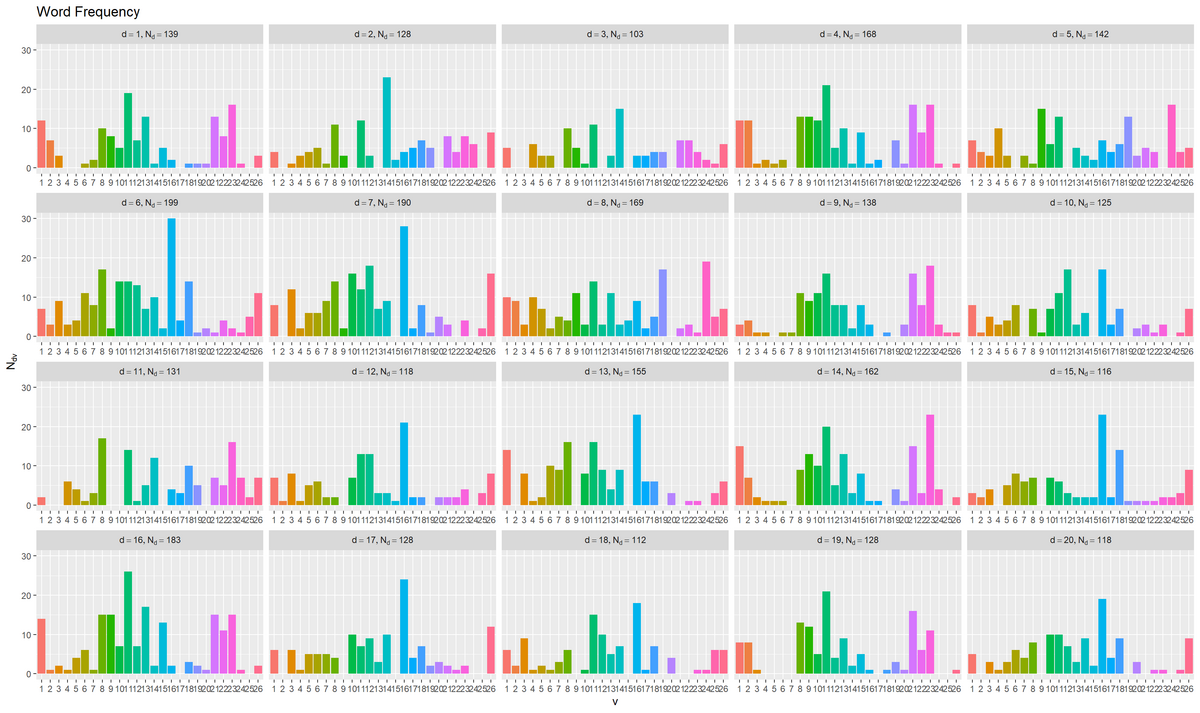
各文書の語彙ごとの出現度数N_dvの作成については「ループあり版」の記事を参照のこと。
推論処理
生成した文書データを用いて、トピック分布と単語分布を推定する。
パラメータの初期化
トピック数を指定して、文書数・語彙数を設定する。
# トピック数を指定 K <- 4 # 文書数と語彙数を取得 D <- nrow(N_dv) V <- ncol(N_dv) D; V
## [1] 20 ## [1] 26
トピック数$K$を指定する。
文書数$D$はN_dvの行数、語彙数$V$は列数に対応する。
トピック分布の初期値を作成する。
# トピック分布θの初期化 theta_k <- runif(n = K, min = 0, max = 1) |> (\(vec) {vec / sum(vec)})() # 正規化 theta_k
## [1] 0.1286487 0.2511032 0.2625641 0.3576840
K個の一様乱数をrunif()で生成し、総和で割って正規化して、トピック分布$\boldsymbol{\theta} = (\theta_1, \cdots, \theta_K)$、$0 \leq \theta_k \leq 1$、$\sum_{k=1}^K \theta_k = 1$の初期値とする。
作図用に、生成した値をデータフレームに格納する。
# 作図用のデータフレームを作成 topic_df <- tibble::tibble( topic = factor(1:K), # トピック番号 probability = theta_k # 割り当て確率 ) topic_df
## # A tibble: 4 × 2 ## topic probability ## <fct> <dbl> ## 1 1 0.129 ## 2 2 0.251 ## 3 3 0.263 ## 4 4 0.358
因子型の1からKの整数をトピック番号列として、対応する確率とあわせて格納する。
トピック分布の初期値をグラフで確認する。
# 推定トピック分布を作図 ggplot() + geom_bar(data = topic_df, mapping = aes(x = topic, y = probability, fill = topic), stat = "identity", show.legend = FALSE) + # トピック分布 labs(title = "Topic Distribution", subtitle = "initial", x = "k", y = expression(theta[k]))
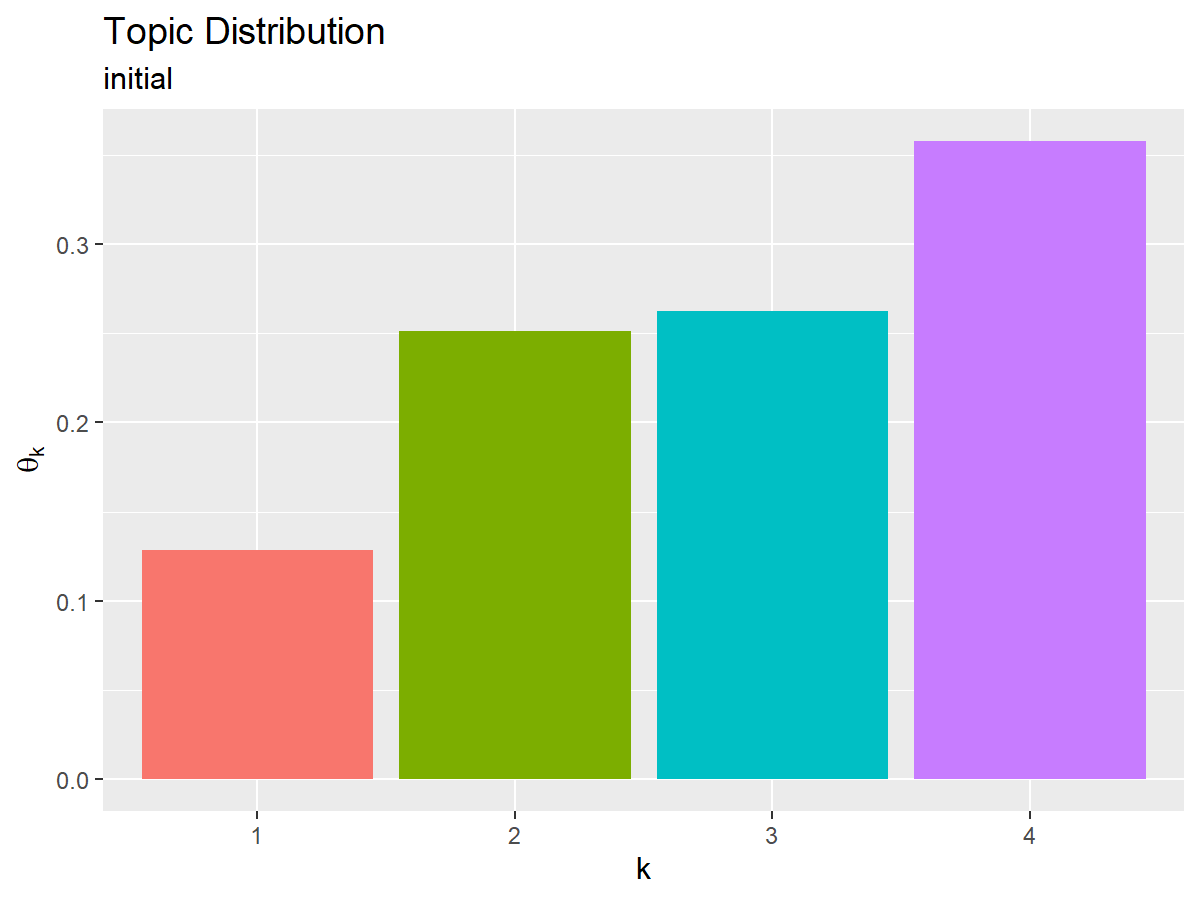
x軸をトピック番号、y軸を各トピックとなる確率として棒グラフを描画する。
同様に、単語分布の初期値を作成する。
# 単語分布Φの初期化 phi_kv <- runif(n = K*V, min = 0, max = 1) |> matrix(nrow = K, ncol = V) |> (\(mat) {mat / rowSums(mat)})() # 正規化 phi_kv[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.010529477 0.02535184 0.07196873 0.02451621 0.00079193 ## [2,] 0.063643837 0.06286962 0.04408125 0.07131599 0.03834561 ## [3,] 0.009735611 0.03692055 0.06009110 0.02494965 0.00894352 ## [4,] 0.005793178 0.05443036 0.04120702 0.03215909 0.04216439
K×V個の一様乱数を生成してK行V列のマトリクスに整形し、行ごとの和で割って正規化して、K個の単語分布$\boldsymbol{\Phi} = \{\boldsymbol{\phi}_1, \cdots, \boldsymbol{\phi}_K\}$、$\boldsymbol{\phi}_k = (\phi_{k1}, \cdots, \phi_{kV})$、$0 \leq \phi_{kv} \leq 1$、$\sum_{v=1}^V \phi_{kv} = 1$の初期値とする。
生成した値をデータフレームに格納する。
# 作図用のデータフレームを作成 word_df <- phi_kv |> tibble::as_tibble() |> tibble::add_column( topic = factor(1:K) # トピック番号 ) |> tidyr::pivot_longer( cols = !topic, names_to = "vocabulary", # 列名を語彙番号に変換 names_prefix = "V", names_ptypes = list(vocabulary = factor()), values_to = "probability" # 出現確率列をまとめる ) word_df
## # A tibble: 104 × 3 ## topic vocabulary probability ## <fct> <fct> <dbl> ## 1 1 1 0.0105 ## 2 1 2 0.0254 ## 3 1 3 0.0720 ## 4 1 4 0.0245 ## 5 1 5 0.000792 ## 6 1 6 0.0664 ## 7 1 7 0.0299 ## 8 1 8 0.0427 ## 9 1 9 0.0635 ## 10 1 10 0.0349 ## # … with 94 more rows
phi_kvはK行V列のマトリクスなので、as_tibble()でデータフレームに変換して、トピック番号列を追加する。
さらに、pivot_longer()で語彙ごと(V列)の出現確率列を1列にまとめる。データフレームの変換時に列名が"V"に通し番号を付けた文字列になるので、names_prefix引数で先頭の"V"を取り除き、names_ptypes引数で因子型に変換して、語彙番号列とする。
トピックごとの単語分布の初期値をグラフで確認する。
# 推定単語分布を作図 ggplot() + geom_bar(data = word_df, mapping = aes(x = vocabulary, y = probability, fill = vocabulary), stat = "identity", show.legend = FALSE) + # 単語分布 facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic)), scales = "free_x") + # 分割 labs(title = "Word Distribution", subtitle = "initial", x = "v", y = expression(phi[kv]))
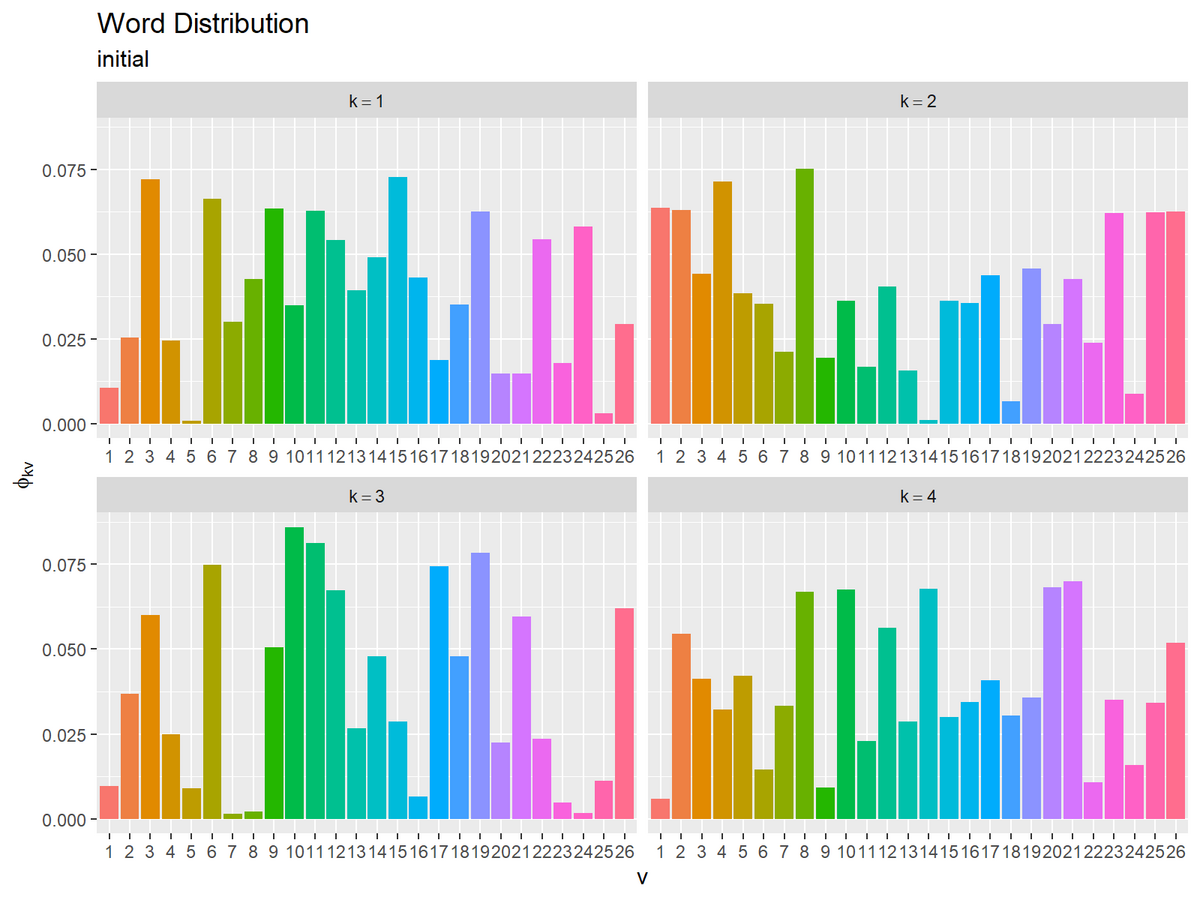
x軸を語彙番号、y軸を各語彙となる確率として棒グラフを描画する。
facet_wrap()にトピック番号列を指定して、トピックごとにグラフを分割して描画する。
ここまでで、推論処理の準備ができた。続いて、推論処理を行う。
コード全体
試行回数を指定して、トピック分布と単語分布の更新を繰り返す。
# 試行回数を指定 MaxIter <- 20 # 推移の確認用の受け皿を作成 trace_theta_ki <- matrix(NA, nrow = K, ncol = MaxIter+1) trace_phi_kvi <- array(NA, dim = c(K, V, MaxIter+1)) # 初期値を保存 trace_theta_ki[, 1] <- theta_k trace_phi_kvi[, , 1] <- phi_kv # EMアルゴリズムによる最尤推定 for(i in 1:MaxIter){ # 負担率qの計算:式(3.3) log_term_dk <- t(log(theta_k + 1e-7) + log(phi_kv + 1e-7) %*% t(N_dv)) # 分子 log_term_dk <- log_term_dk - apply(log_term_dk, MARGIN = 1, FUN = min) # アンダーフロー対策 log_term_dk <- log_term_dk - apply(log_term_dk, MARGIN = 1, FUN = max) # オーバーフロー対策 q_dk <- exp(log_term_dk) / rowSums(exp(log_term_dk)) # 正規化 # トピック分布θの計算:式(3.7) new_theta_k <- colSums(q_dk) # 分子 theta_k <- new_theta_k / sum(new_theta_k) # 正規化 # 単語分布Φの計算:式(3.8) new_phi_kv <- t(q_dk) %*% N_dv # 分子 phi_kv <- new_phi_kv / rowSums(new_phi_kv) # 正規化 # i回目の更新値を保存 trace_theta_ki[, i+1] <- theta_k trace_phi_kvi[, , i+1] <- phi_kv # 動作確認 message("\r", i, "/", MaxIter, appendLF = FALSE) }
推移の確認用に、トピック分布と単語分布の初期値と更新値をそれぞれtrace_***に格納していく。
コードの解説
繰り返し行う更新処理をそれぞれ確認する。
Eステップ
Eステップでは、前ステップで更新した(または初期値の)トピック分布$\boldsymbol{\theta}$と単語分布$\boldsymbol{\Phi}$を用いて、負担率$\mathbf{q}$を更新する。各文書の負担率$\mathbf{q}_d = (q_{d1}, \cdots, q_{dK})$をまとめて、$\mathbf{q} = \{\mathbf{q}_1, \cdots, \mathbf{q}_D\}$とする。
次の処理によって、負担率を更新(計算)する。
# 負担率qの初期化 q_dk <- matrix(0, nrow = D, ncol = K) # 負担率qの計算:式(3.3) log_term_dk <- t(log(theta_k + 1e-7) + log(phi_kv + 1e-7) %*% t(N_dv)) # 分子 log_term_dk <- log_term_dk - apply(log_term_dk, MARGIN = 1, FUN = min) # アンダーフロー対策 log_term_dk <- log_term_dk - apply(log_term_dk, MARGIN = 1, FUN = max) # オーバーフロー対策 q_dk <- exp(log_term_dk) / rowSums(exp(log_term_dk)) # 正規化 q_dk[1:5, ]
## [,1] [,2] [,3] [,4] ## [1,] 2.208403e-50 1.000000e+00 3.736484e-77 3.482370e-53 ## [2,] 3.310597e-42 5.744215e-47 1.000000e+00 7.713281e-35 ## [3,] 1.855999e-26 1.115036e-30 1.000000e+00 1.110970e-30 ## [4,] 5.699016e-53 1.000000e+00 1.167746e-114 3.648963e-78 ## [5,] 1.000000e+00 8.281689e-52 2.799567e-68 3.447614e-68
負担率の各要素の更新式は、次の式である。
この式のまま計算すると、指数の計算においてアンダーフローの可能性がある。そこで、この式の分子を$\tilde{q}_{dk}$とおき、対数をとって計算する。
$\log \tilde{q}_{dk}\ (d = 1, \dots, D,\ k = 1, \dots, K)$について、$(D \times K)$の行列log_term_dkとすると、2つの行列の積に分解できる。
度数$N_{dv}\ (d = 1, \dots, D,\ v = 1, \dots, V)$を並べた$(D \times V)$の行列と、対数をとった出現確率$\log \phi_{kv}\ (k = 1, \dots, K,\ v = 1, \dots, V)$を並べた$(V \times K)$の行列の積で計算できる。後の項は、$\boldsymbol{\Phi}$を$(K \times V)$の行列として、転置して要素ごとに対数をとった行列と言える。
さらに、最小値を引くことでアンダーフロー、最大値を引くことでオーバーフローが起きにくくする。また、$\log 0$は計算できないので、結果に影響しないほどの小さい値1e-7を加えて計算する。
$x = \exp(\log x)$より、$\log$を外して総和で割って正規化する。
log_term_dkの行方向の和が$\sum_k$の計算に対応する。
Mステップ
Mステップでは、Eステップで更新した負担率$\mathbf{q}$を用いて、トピック分布$\boldsymbol{\theta}$と単語分布$\boldsymbol{\Phi}$を更新する。
次の処理によって、トピック分布を更新する。
# トピック分布θの計算:式(3.7) new_theta_k <- colSums(q_dk) # 分子 res_theta_k <- new_theta_k / sum(new_theta_k) # 正規化 new_theta_k; res_theta_k
## [1] 2 6 3 9 ## [1] 0.10 0.30 0.15 0.45
トピック分布の各要素の更新式は、次の式である。
この式の分子を$\tilde{\theta}_k$とおいて計算する。
$\tilde{\theta}_k\ (k = 1, \dots, K)$について、$K$次元のベクトルnew_theta_kとする。q_dkの列方向の和が$\sum_d$の計算に対応する。
$\tilde{\theta}_k$を総和で割って正規化する。
(次にやる作図処理に影響しないように変数名をres_***にしている。)
続いて、次の処理によって、単語分布を更新する。
# 単語分布Φの計算:式(3.8) new_phi_kv <- t(q_dk) %*% N_dv # 分子 res_phi_kv <- new_phi_kv / rowSums(new_phi_kv) # 正規化 new_phi_kv[, 1:5]; res_phi_kv[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 17 1.3000e+01 6 20 10 ## [2,] 64 3.9000e+01 10 5 6 ## [3,] 11 3.9391e-48 1 15 11 ## [4,] 64 9.0000e+00 64 13 36 ## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.05466238 4.180064e-02 0.019292605 0.064308682 0.032154341 ## [2,] 0.06971678 4.248366e-02 0.010893246 0.005446623 0.006535948 ## [3,] 0.03038674 1.088149e-50 0.002762431 0.041436464 0.030386740 ## [4,] 0.05075337 7.137193e-03 0.050753370 0.010309278 0.028548771
単語分布の各要素の更新式は、次の式である。
この式の分子を$\tilde{\phi}_{kv}$とおいて計算する。
$\tilde{\phi}_{kv}\ (k = 1, \dots, K,\ v = 1, \dots, V)$について、$(K \times V)$の行列new_phi_kvとすると、2つの行列の積に分解できる。
負担率$q_{dk}\ (d = 1, \dots, D,\ k = 1, \dots, K)$を並べた$(K \times D)$の行列と、度数$N_{dv}\ (d = 1, \dots, D,\ v = 1, \dots, V)$を並べた$(D \times V)$の行列の積で計算できる。前の項は、$\mathbf{q}$を$(D \times K)$の行列として、転置した行列と言える。
$\tilde{\phi}_{kv}$を$v$(行)についての和で割って正規化する。
以上が、1ステップでの更新処理である。この処理を指定した回数繰り返し行う。
推論結果の可視化
推定したトピック分布と単語分布を可視化する。詳しくは「ループあり版」の記事を参照のこと。
トピック分布と単語分布をそれぞれ真の分布と重ねてグラフを作成する。
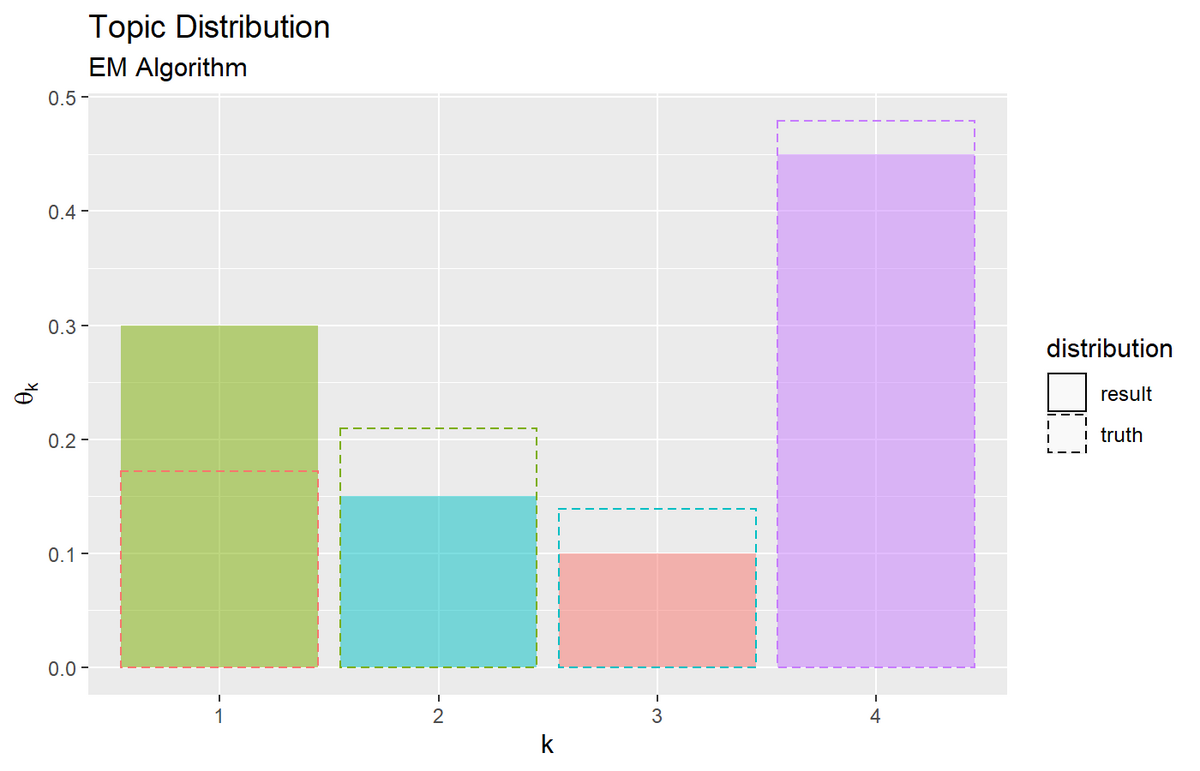
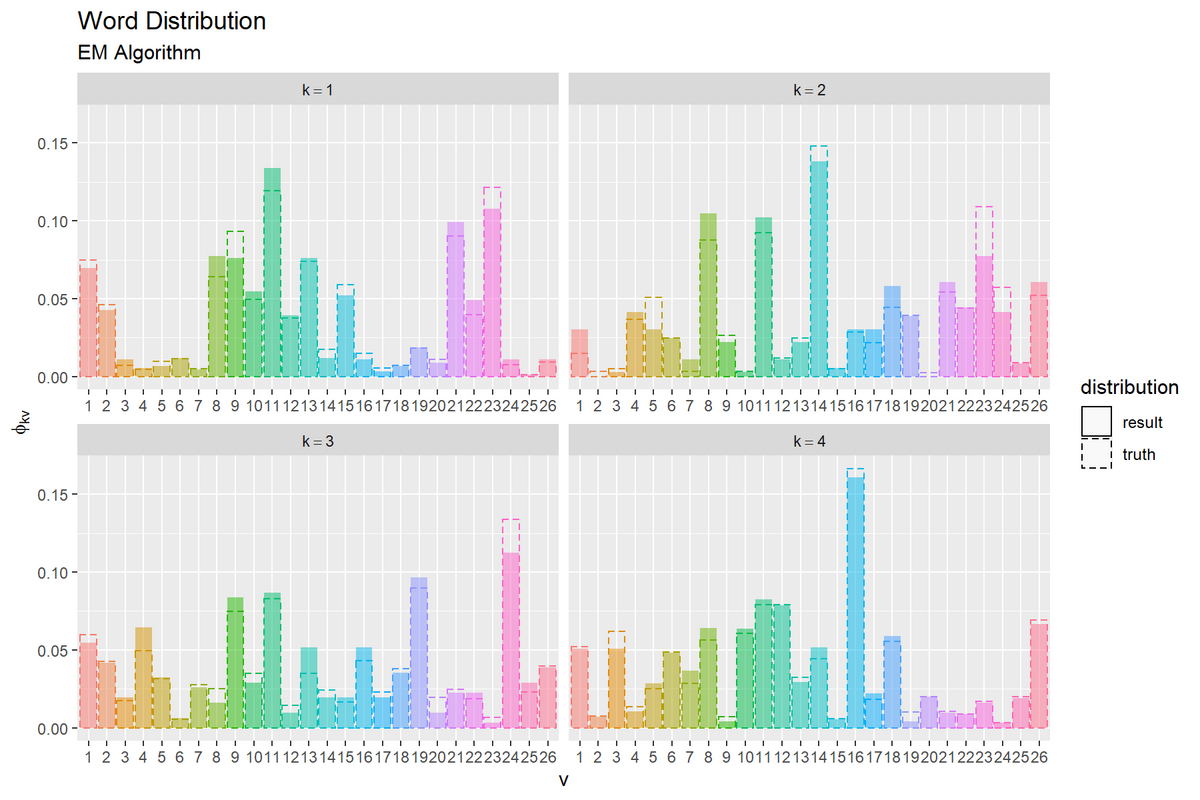
トピック分布と単語分布のアニメーションを作成する。

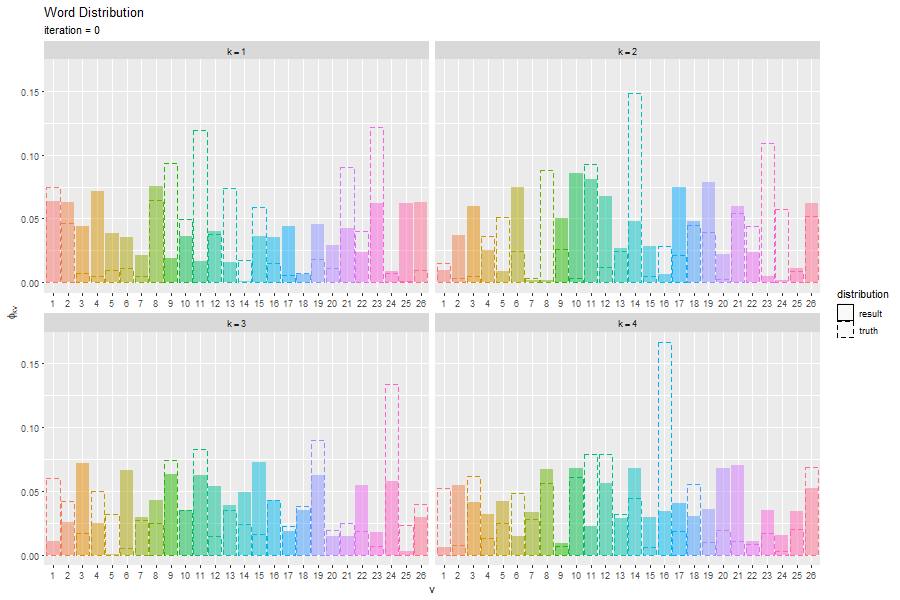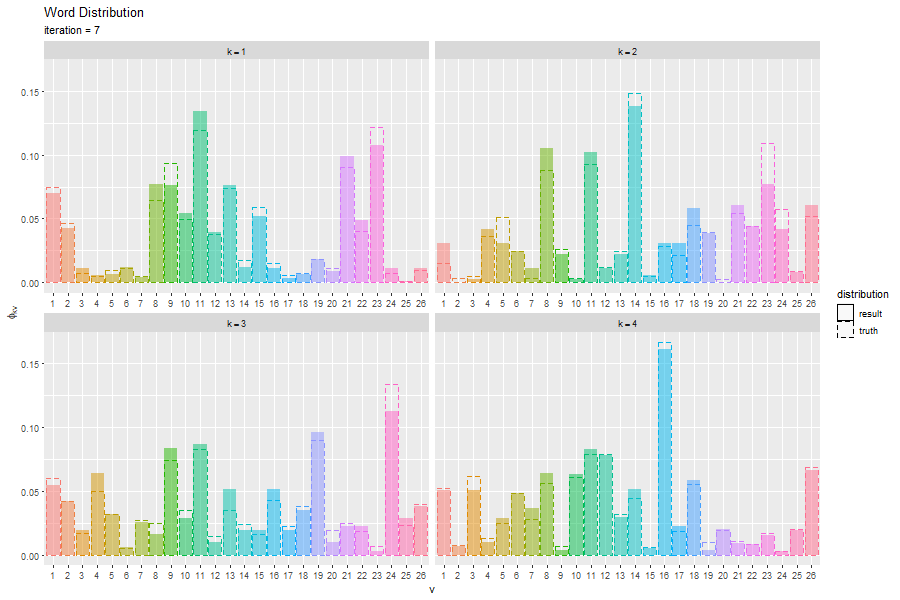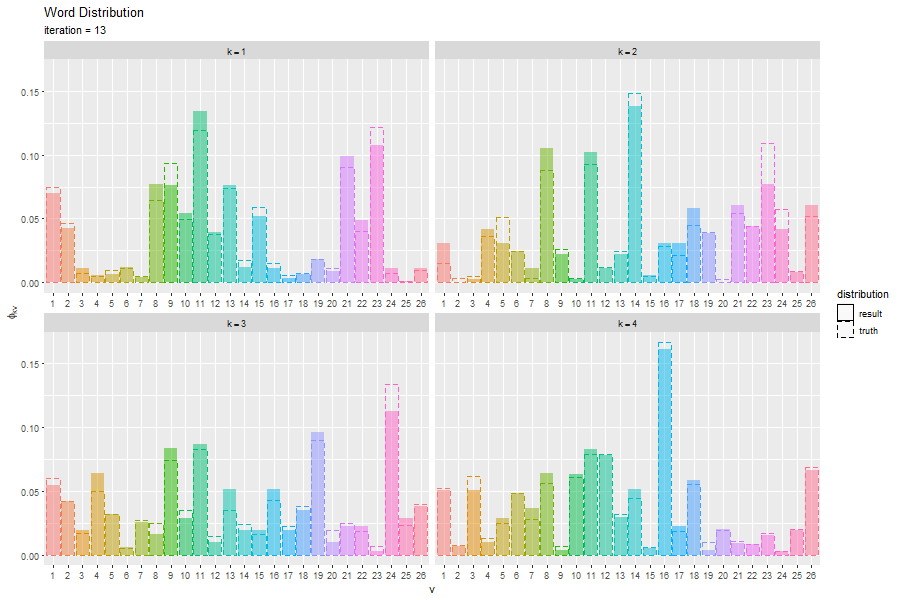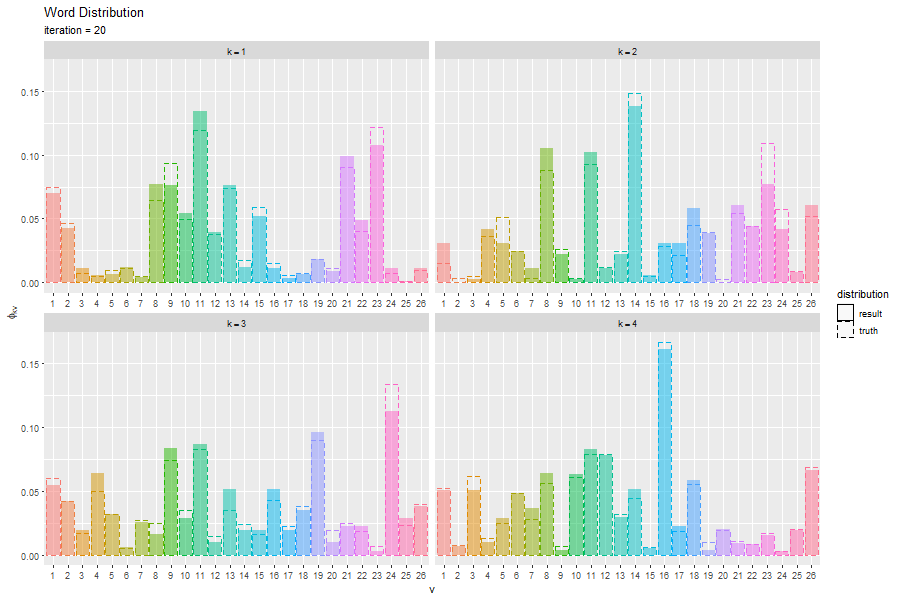
この記事では、EMアルゴリズムによる最尤推定を実装した。次の記事では、変分ベイズ推論を実装する。
参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
修正作業のついでにループなしで組んでみました。また青トピ本の新規記事を書くことがあろうとは感動です。
現在第3稿として(1年以上空きつつも)書いてるのですが、第2稿の頃にループを使わずに組もうとしていました。が、その時は3重ループの内の1つを取り除き切れませんでした。その後、行列計算を勉強したおかげで3つとも置き替えられました。まさか、アンダーフロー対策の対数化の結果、行列計算に落とし込めるとは。
大外のループは残ってますが、これはアルゴリズムの意図を明示するために必要な処理です!
【次節の内容】
つづく