はじめに

　『スタンフォード　ベクトル・行列からはじめる最適化数学』の学習ノートです。
　「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。

　この記事は3.2節「距離」の内容です。
　ユークリッド距離による最近傍を可視化します。

【前の内容】

www.anarchive-beta.com

【他の内容】

www.anarchive-beta.com

【今回の内容】

はじめに
最近傍の可視化
- 2次元の場合
- 3次元の場合
参考書籍
おわりに

最近傍の可視化

　ユークリッド距離(euclidean distance)を用いて、最近傍(nearest neighbor)をグラフで確認します。
　ユークリッド距離については「【Python】3.2：ユークリッド距離の可視化【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。

　利用するライブラリ読み込みます。

# 利用ライブラリ
import numpy as np
import matplotlib.pyplot as plt

2次元の場合

　まずは、2次元空間(平面)上で最近傍なサンプル点を可視化します。

　基準とする2次元ベクトルを指定します。

# 基準のベクトル(座標)を指定
x = np.array([2.0, 1.0])

　 $\mathbf{x} = (x_1, x_2)^{\top}$ をxとして値を指定します。ただし、Pythonでは0からインデックスが割り当てられるので、 $x_1$ の値はx[0]に対応します。

　データ数を指定して、2次元ベクトルをランダムに作成します。

# データ数を指定
N = 10

# ベクトル(座標)を生成
Z = np.random.uniform(low=-10, high=10, size=(N, 2))
print(Z.round(2))

[[-7.65 -1.83]
 [-9.82  3.09]
 [-9.71 -7.31]
 [ 5.96 -1.28]
 [ 9.08 -9.6 ]
 [ 3.37  6.07]
 [ 0.57  5.35]
 [ 4.55 -2.77]
 [-5.45 -0.73]
 [ 2.3   3.78]]

　np.random.uniform()で一様乱数を生成します。乱数の下限をlow引数、上限をhigh引数に指定します。また、サンプルサイズ(出力する配列の形状)をsize引数に指定します。
　N行2列の配列Zを作成して、各行を1つのベクトル(座標) $\mathbf{z}_n = (z_1, z_2)^{\top}$ とします。

　2次元空間上の基準点とデータ点の距離を描画します。

# 作図用の値を取得
x_min = np.floor(np.min([x[0], *Z[:, 0]])) - 1
x_max = np.ceil(np.max([x[0], *Z[:, 0]])) + 1
y_min = np.floor(np.min([x[1], *Z[:, 1]])) - 1
y_max = np.ceil(np.max([x[1], *Z[:, 1]])) + 1

# ラベル配置の調整用のリストを作成
loc_y_lt = ['top', 'bottom']

# 基準点とデータ点の距離を作図
fig, ax = plt.subplots(figsize=(7, 7), facecolor='white')
ax.scatter(*x, label='$x$') # 基準点x
ax.scatter(*Z.T, label='$z_n$') # データ点z
ax.quiver(*np.tile(x, reps=(N, 1)).T, *(Z-x).T, color='gray', width=0.005, 
          angles='xy', scale_units='xy', scale=1, label='$\|x - z_n\|$') # ベクトルz-x
for n in range(N):
    # n番目のデータを取得
    z = Z[n]
    
    # 2点の距離を計算
    dist_xz = np.sqrt(np.sum((z - x)**2)) # 定義式
    #dist_xz = np.linalg.norm(z - x) # NumPy関数
    
    # 基準点との位置関係により配置を調整
    loc_y_idx = int(z[1] >= x[1])
    
    # ラベルを描画
    ax.text(*z, s='('+', '.join(map(str, z.round(1)))+')', 
             ha='center', va=loc_y_lt[loc_y_idx]) # 座標zラベル
    ax.text(*0.5*(x+z), s=str(dist_xz.round(2)), 
            ha='center', va='center') # 距離x,zラベル
ax.set_xticks(ticks=np.arange(x_min, x_max+1))
ax.set_yticks(ticks=np.arange(y_min, y_max+1))
ax.grid()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('x=('+', '.join(map(str, x))+')', loc='left')
fig.suptitle('euclidean distance', fontsize=20)
ax.legend()
ax.set_aspect('equal')
plt.show()

　ベクトル $\mathbf{z}_n - \mathbf{x}$ のグラフをaxes.quiver()で描画します。第1・2引数に始点の座標、第3・4引数にベクトルのサイズ(変化量)を指定します。
　配列x, zの前に*を付けてアンパック(展開)して指定しています。

　また、「データ点 $\mathbf{z}_n$ の座標」と「基準点 $\mathbf{x}$ との距離 $\mathrm{dist}(\mathbf{x}, \mathbf{z}_n) = |\mathbf{z}_n - \mathbf{a}|$ 」をラベルとして描画します。
　ユークリッド距離(差のユークリッドノルム) $|\mathbf{b} - \mathbf{a}| = \sqrt{\sum_{i=1}^n (b_i - a_i)} = \sqrt{(\mathbf{b} - \mathbf{a})^{\top} (\mathbf{b} - \mathbf{a})}$ は、平方根np.sqrt()や内積np.dot()を使って計算できます。または、np.linalg.norm()で直接計算できます。

　全てのデータの距離を一度に計算します。

# (全てのデータの)距離を計算
dist_xZ = np.sqrt(np.sum((Z - x)**2, axis=1))
dist_xZ = np.sqrt(np.diag(np.dot(Z-x, (Z-x).T)))
dist_xZ = np.linalg.norm(Z - x, axis=1)
print(dist_xZ)

[10.06057186 12.00153938 14.357526    4.5704046  12.74811029  5.25256641
  4.57758371  4.54996467  7.64415809  2.79491539]

　.Tで転置やnp.diag()で対角要素の抽出、axis引数で和をとる軸を指定して計算します。

　距離の最小値と、距離が最小となるデータ番号(インデックス)を抽出します。

# 距離の最小値とデータ番号を取得
min_dist = np.min(dist_xZ)
min_n = np.argmin(dist_xZ)
print(min_dist)
print(min_n)

2.7949153893092427
9

　np.min()で最小値、np.argmin()で最小値のインデックスを抽出します。

　最近傍な点を描画します。

# 最近傍データを抽出
min_z = Z[min_n]

# 最近傍点を作図
fig, ax = plt.subplots(figsize=(7, 7), facecolor='white')
ax.scatter(*x) # 基準点x
ax.scatter(*Z.T) # データ点z
ax.quiver(*x, *min_z-x, ec='red', linewidth=1.5, 
          scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1) # 線分xz
ax.text(*x, s='$x$', size=15, ha='right', va='top') # 基準点xラベル
for n in range(N):
    # n番目のデータを取得
    z = Z[n]
    
    # ラベルを描画
    ax.text(*z, s='$z_{'+str(n+1)+'}$', size=15, 
             ha='center', va='bottom') # 座標zラベル
ax.set_xticks(ticks=np.arange(x_min, x_max+1))
ax.set_yticks(ticks=np.arange(y_min, y_max+1))
ax.grid()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('$x$=('+', '.join(map(str, x))+'), ' + 
             '$argmin_n$ dist($x, z_n$)='+str(min_n+1)+', ' + 
             '$\|z_{'+str(min_n+1)+'} - x\|$='+str(min_dist.round(2)), loc='left')
fig.suptitle('nearest neighbor', fontsize=20)
ax.set_aspect('equal')
plt.show()

　最近傍の点をmin_zとして作図します。

3次元の場合

　続いて、3次元空間上で最近傍なサンプル点を可視化します。

　基準とする3次元ベクトルを指定します。

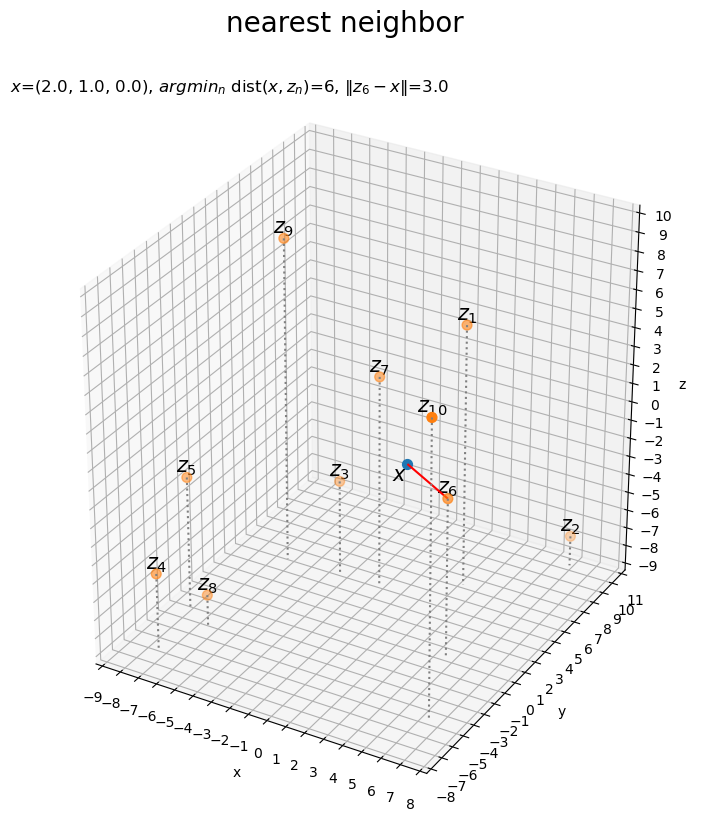
# 基準のベクトル(座標)を指定
x = np.array([2.0, 1.0, 0.0])

　 $\mathbf{x} = (x_1, x_2, x_3)^{\top}$ をxとして値を指定します。

　データ数を指定して、3次元ベクトルをランダムに作成します。

# データ数を指定
N = 10

# ベクトル(座標)を生成
Z = np.random.uniform(low=-10, high=10, size=(N, 3))
print(Z.round(2))

[[ 2.47  5.71  5.2 ]
 [ 6.1   9.84 -7.35]
 [-3.11  3.52 -3.74]
 [-7.07 -6.5  -4.74]
 [-7.83 -2.53 -1.82]
 [ 4.75 -0.11 -0.46]
 [-1.01  3.68  2.47]
 [-6.28 -3.43 -7.34]
 [-6.05  3.5   8.5 ]
 [ 6.69 -5.22  6.88]]

　N行3列の配列Zを作成して、各行を1つのベクトル(座標) $\mathbf{z}_n = (z_1, z_2, z_3)^{\top}$ とします。

　3次元空間上の基準点とデータ点の距離を描画します。

# 作図用の値を取得
x_min = np.floor(np.min([x[0], *Z[:, 0]])) - 1
x_max = np.ceil(np.max([x[0], *Z[:, 0]])) + 1
y_min = np.floor(np.min([x[1], *Z[:, 1]])) - 1
y_max = np.ceil(np.max([x[1], *Z[:, 1]])) + 1
z_min = np.floor(np.min([x[2], *Z[:, 2]])) - 1
z_max = np.ceil(np.max([x[2], *Z[:, 2]])) + 1

# ラベル配置の調整用のリストを作成
loc_y_lt = ['top', 'bottom']

# 基準点とデータ点の距離を作図
fig, ax = plt.subplots(figsize=(9, 9), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.scatter(*x, s=50, label='$x$') # 基準点x
ax.scatter(*Z.T, s=50, label='$z_n$') # データ点z
ax.quiver(*np.tile(x, reps=(N, 1)).T, *(Z-x).T, color='gray', 
          arrow_length_ratio=0.05, label='$\|x - z_n\|$') # ベクトルz-x
for n in range(N):
    # n番目のデータを取得
    z = Z[n]
    
    # 2点の距離を計算
    dist_xz = np.sqrt(np.sum((z - x)**2)) # 定義式
    #dist_xz = np.linalg.norm(z - x) # NumPy関数
    
    # 基準点との位置関係により配置を調整
    loc_y_idx = int(z[1] >= x[1])
    
    # ラベルを描画
    ax.text(*z, s='('+', '.join(map(str, z.round(1)))+')', 
            size=7, ha='center', va=loc_y_lt[loc_y_idx], zorder=100) # 座標zラベル
    ax.text(*0.5*(x+z), s=str(dist_xz.round(2)), 
            size=7, ha='center', va='center', zorder=100) # 距離x,zラベル
ax.set_xticks(ticks=np.arange(x_min, x_max+1))
ax.set_yticks(ticks=np.arange(y_min, y_max+1))
ax.set_zticks(ticks=np.arange(z_min, z_max+1))
ax.grid()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('x=('+', '.join(map(str, x))+')', loc='left')
fig.suptitle('euclidean distance', fontsize=20)
ax.legend()
ax.set_aspect('equal')
plt.show()

　axes.quiver()の第1・2・3引数に始点の座標、第4・5・6引数にベクトルのサイズを指定します。

　また、「各データ点の座標」と「基準点との距離」をラベルとして描画します。
　「2次元の場合」と同じコードで距離を計算できます。

　全てのデータの距離を一度に計算します。

# (全てのデータの)距離を計算
dist_xZ = np.sqrt(np.sum((Z - x)**2, axis=1))
dist_xZ = np.sqrt(np.diag(np.dot(Z-x, (Z-x).T)))
dist_xZ = np.linalg.norm(Z - x, axis=1)
print(dist_xZ)

[ 7.03146758 12.20617985  6.81201181 12.6938103  10.60741463  2.998641
  4.72609882 11.91945673 11.97074009 10.39322151]

　「2次元の場合」と同じコードで計算できます。

　距離の最小値と、距離が最小となるデータ番号(インデックス)を抽出します。

# 距離の最小値とデータ番号を取得
min_dist = np.min(dist_xZ)
min_n = np.argmin(dist_xZ)
print(min_dist)
print(min_n)

2.9986409975100474
5

　「2次元の場合」と同じコードで処理できます。

　最近傍な点を描画します。

# 最近傍データを抽出
min_z = Z[min_n]

# 最近傍点を作図
fig, ax = plt.subplots(figsize=(9, 9), facecolor='white', 
                       subplot_kw={'projection': '3d'})
ax.scatter(*x, s=50) # 基準点x
ax.scatter(*Z.T, s=50) # データ点z
ax.quiver(*x, *min_z-x, color='red', arrow_length_ratio=0.0) # 線分xz
ax.text(*x, s='$x$', size=15, ha='right', va='top') # 基準点xラベル
for n in range(N):
    # n番目のデータを取得
    z = Z[n]
    
    # ラベルを描画
    ax.text(*z, s='$z_{'+str(n+1)+'}$', 
            size=15, ha='center', va='bottom') # 座標zラベル
ax.quiver(Z[:, 0], Z[:, 1], np.repeat(z_min, N), 
          np.zeros(N), np.zeros(N), Z[:, 2]-z_min, 
          color='gray', arrow_length_ratio=0, linestyle=':') # 補助線
ax.set_xticks(ticks=np.arange(x_min, x_max+1))
ax.set_yticks(ticks=np.arange(y_min, y_max+1))
ax.set_zticks(ticks=np.arange(z_min, z_max+1))
ax.set_zlim(z_min, z_max)
ax.grid()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('$x$=('+', '.join(map(str, x))+'), ' + 
             '$argmin_n$ dist($x, z_n$)='+str(min_n+1)+', ' + 
             '$\|z_{'+str(min_n+1)+'} - x\|$='+str(min_dist.round(2)), loc='left')
fig.suptitle('nearest neighbor', fontsize=20)
ax.set_aspect('equal')
plt.show()