はじめに
「プログラミング」初学者のための『ゼロから作るDeep Learning』攻略ノートです。『ゼロつくシリーズ』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
関数やクラスとして実装される処理の塊を細かく分解して、1つずつ実行結果を見ながら処理の意図を確認していきます。
この記事は、3.5節「出力層の設計」の内容です。Softmax関数をPythonで実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
3.5 ソフトマックス関数の実装
他クラス(多値)分類問題においてニューラルネットワークの最終層の活性化関数として用いられるソフトマックス関数(Softmax関数)を実装します。
利用するライブラリを読み込みます。
# 3.5節で利用するライブラリ import numpy as np
3.5.1 ソフトマックス関数
ソフトマックス関数の定義式を確認します。
・数式の確認(1)
まずは、ソフトマックス関数(Softmax関数)の定義式を確認します。
ソフトマックス関数は、次の式で定義されます。
$K$個の要素$\mathbf{a} = (a_0, a_1, \cdots, a_{K-1})$を入力して、$0 \leq y_k \leq 1$、$\sum_{k=0}^{K-1} y_k = 1$となる$\mathbf{y} = (y_0, y_1, \cdots, y_{K-1})$を出力します。Pythonのインデックスに合わせて添字を0から割り当てています。
$y_k$は、0から1の値をとり、$K$個の要素の和が1になります。この性質から、$y_k$を「入力がクラス$k$である確率」、$\mathbf{y}$を「$K$個のクラスに対する確率分布」と解釈できます。
ソフトマックス関数は、入力を確率(のよう)に変換できることから、多クラス(多値)分類問題においてニューラルネットワークの最終層(出力層)の活性化関数に使われます。
本では、「ニューラルネットワークの入力を$\mathbf{x}$」、$\mathbf{x}$から求めた「ニューラルネットワークの最終層の重み付き和を$\mathbf{a}$」で表します。ソフトマックス関数に$\mathbf{a}$を入力して、0から1の値に正規化された$\mathbf{y}$を出力します。「$\mathbf{y}$はニューラルネットワークの出力」でもあります。
この資料では、ソフトマックス関数によって0から1の値に変換することを「正規化する」と表現します。
定義式について「ソフトマックス関数のオーバーフロー対策【ゼロつく1のノート(数学)】 - からっぽのしょこ」でもう少し深く確認します。
・処理の確認(1)
次に、ソフトマックス関数で行う処理を確認します。とりあえず定義式の通りに実装してみましょう(このままだと問題が生じます)。
入力(この本では最終層の重み付き和)$\mathbf{a}$を作成します。
# 仮の入力(重み付き和)を作成 a = np.array([-1.5, 1.0, 3.0]) print(a)
[-1.5 1. 3. ]
分子の計算をします。指数関数$\exp(\cdot)$の計算は、np.exp()で行えます。
# 指数をとる exp_a = np.exp(a) print(exp_a)
[ 0.22313016 2.71828183 20.08553692]
指数をとると正の値になります。
分子の値exp_aの総和が分母の値となります。
# 和をとる sum_exp_a = np.sum(exp_a) print(sum_exp_a)
23.02694891179514
分子の値exp_aを分母の値sum_exp_aで割って、定義式全体の計算をします。
# 式(3.10)の計算 y = exp_a / sum_exp_a print(np.round(y, 3)) print(np.sum(y))
[0.01 0.118 0.872]
1.0
総和で割ると、全ての要素が0から1の値になり、またその総和が1になります。
処理の確認ができたので、ソフトマックス関数を関数として実装します。
# ソフトマックス関数の実装 def softmax(a): # 式(3.10)の計算 exp_a = np.exp(a) # 分子 sum_exp_a = np.sum(exp_a) # 分母 y = exp_a / sum_exp_a # 式(3.10) return y
実装した関数を試してみましょう。
# ソフトマックス関数による活性化(正規化) y = softmax(np.array([-1.5, 1.0, 3.0])) print(np.round(y, 3)) print(np.sum(y))
[0.01 0.118 0.872]
1.0
定義式の通りに実装できました。
しかしこのままだと、入力する値が大きいときとオーバーフローしてしまいます。
# ソフトマックス関数による活性化(正規化) y = softmax(np.array([1010, 1000, 900])) print(y)
[nan nan nan]
指数をとることで値が大きくなりすぎたため、オーバーフローが発生しました。ただし、ソフトマックス関数の出力自体は0から1という小さい値になるのでした。そこで、途中計算でオーバーフローが起こりにくいように計算する必要があります。
3.5.2 オーバーフロー対策版ソフトマックス関数
オーバーフローが発生しにくいソフトマックス関数の定義式を確認して、実装します。
・数式の確認(2)
続いて、オバーフロー対策を行ったソフトマックス関数(Softmax関数)の定義式を確認します。オーバーフロー対策については「ソフトマックス関数のオーバーフロー対策【ゼロつく1のノート(数学)】 - からっぽのしょこ」を参照してください。
オーバーフロー対策版ソフトマックス関数は、次の式で定義されます。
ソフトマックス関数の入力$\mathbf{a}$の最大値を$a_{\mathrm{max}}$で表します。この式は、入力の全ての要素から最大値を引いた上で、ソフトマックス関数(3.10)の計算をすることを表しています。入力の値を小さくすることで、指数をとった値が大きくなりすぎるのを防ぎます。全ての入力から定数を引いても、出力$\mathbf{y}$には影響しません。
・処理の確認(2)
では、オーバーフローを回避するソフトマックス関数の処理を確認します。
入力を作成して、最大値をcとします。
# 仮の入力(重み付き和)を作成 a = np.array([1010, 1000, 900]) # 最大値を抽出 c = np.max(a) print(c)
1010
入力aの全ての要素から最大値cを引きます。
# 入力と最大値の差を計算 tmp_a = a - c print(tmp_a)
[ 0 -10 -110]
最大値を引くため、0以下の値になります。
tmp_aをソフトマックス関数の入力として、先ほどと同じ処理をします。
# 分子の計算 exp_a = np.exp(tmp_a) print(exp_a) # 分母の計算 sum_exp_a = np.sum(exp_a) print(sum_exp_a) # 式(3.10)の計算 y = exp_a / sum_exp_a print(y) print(np.sum(y))
[1.00000000e+00 4.53999298e-05 1.68891188e-48]
1.0000453999297625
[9.99954602e-01 4.53978687e-05 1.68883521e-48]
1.0
オーバーフローが発生せずに計算できました。
以上がソフトマックス関数で行う処理です。
・実装
処理の確認ができたので、ソフトマックス関数を関数として実装します。
# ソフトマックス関数を実装 def softmax(a): # 式(3.10)の計算 c = np.max(a) # 最大値 exp_a = np.exp(a - c) # 分子:オーバーフロー対策 sum_exp_a = np.sum(exp_a) # 分母 y = exp_a / sum_exp_a # 式(3.10) return y
実装した関数を試してみましょう。
# ソフトマックス関数による活性化(正規化) y = softmax(np.array([1010, 1000, 990])) print(y) print(np.sum(y))
[9.99954600e-01 4.53978686e-05 2.06106005e-09]
1.0
# ソフトマックス関数による活性化(正規化) y = softmax(np.array([-1.5, 1.0, 3.0])) print(np.round(y, 3)) print(np.sum(y))
[0.01 0.118 0.872]
1.0
オーバーフローが発生せず、また先ほどと同じ結果になりました。
以上で、(1次元配列用の)ソフトマックス関数を実装できました。次項では、ソフトマックス関数による活性化前後の変化を確認します。
3.5.3 ソフトマックス関数の特徴
ソフトマックス関数の入力と出力の関係を簡単に確認します。
入力を作成して、ソフトマックス関数で活性化(正規化)します。
# (段々大きくなる)入力を作成 a = np.arange(10) print(a) # ソフトマックス関数による活性化(正規化) y = softmax(a) print(np.round(y, 3)) print(np.sum(y))
[0 1 2 3 4 5 6 7 8 9]
[0. 0. 0.001 0.002 0.004 0.012 0.031 0.086 0.233 0.632]
1.0
ソフトマックス関数によって、(ソフトマックス関数の)入力$\mathbf{a}$は、0から1の値に変換され、その総和が1になるのでした。またこの性質によって、(ソフトマックス関数かつニューラルネットワークの)出力$\mathbf{y}$は、(ニューラルネットワークの)入力$\mathbf{x}$がどのクラスなのかを表す確率分布として扱えるのでした。
このとき、$\mathbf{a}$と$\mathbf{y}$で各要素の大小関係は変わりません。つまり、$\mathbf{a}$の$i$番目の要素$a_i$が最大のとき、$\mathbf{y}$の$i$番目の要素$y_i$が最大になります。また、最大以外も変化しません。
そのため推論時に、確率が一番高いクラスに分類するのであれば、ソフトマックス関数の計算は不要です。2巻で扱う文章生成のように、確率分布に従ってランダムな操作を行う場合には必要です。
また学習時には、正しいクラスに対してどれだけ高い確率を割り当てられたのかを見る必要があるので、ソフトマックス関数の計算を行います。
膨大なデータを処理するには時間コスト等がかかるので、できるだけ処理を減らしたいというのはどの手法でも共通する考え方です。
以上で、3.5節の内容は終了です。次節では、学習済みのパラメータを用いて手書き文字認識(他クラス分類)を行います。
しかし、この節で実装したsoftmax()は1次元配列しか処理できません。commonフォルダのfunctions.pyに実装されているsoftmax()は、多次元配列を処理できるようにしたものです。そこでこの資料では、多次元配列(バッチデータ)に対応したsoftmax()も実装します。
・バッチ版ソフトマックス関数の実装
3.5.1項では、1つのデータに対するソフトマックス関数を実装しました。ここでは、複数のデータを処理できるソフトマックス関数を実装します。複数のデータ(バッチデータ)については3.6.3項で解説します。また、多次元配列に対応したソフトマックス関数を実際に使うのは4.5節以降です。必要になったタイミングで読んでください。
・数式の確認
まずは、バッチデータに対するソフトマックス関数(Softmax関数)の定義式を確認します。
ソフトマックス関数の入力を$\mathbf{A}$、出力を$\mathbf{Y}$として、それぞれ次の形状とします。
$N$はバッチサイズ、$K$はクラス数です。ソフトマックス関数の入出力で形状は変化しません。Pythonのインデックスに合わせて添字を0から割り当てています。
ただし、ソフトマックス関数はデータ(行)ごとに作用します。つまり、$n$番目($n$行目)の入力$\mathbf{a}_n = (a_{n,0}, a_{n,1}, \cdots, a_{n,K-1})$に対して、次の計算をします。
$n$番目($n$行目)の出力$\mathbf{y}_n = (y_{n,0}, y_{n,1}, \cdots, y_{n,K-1})$が、$0 \leq y_{n,k} \leq 1$、$\sum_{k=0}^{K-1} y_{n,k} = 1$となるように正規化されます。$y_{n,k}$は$n$番目のデータが「$k$番目のクラスである確率」、$\mathbf{y}_n$は$n$番目のデータの「$K$個のクラスに対する確率分布」として解釈できます。
実装においてはオバーフロー対策のために、データ(行)ごとに最大値を引いた上で、式(3.10')の計算をします。$n$番目のデータにおける最大値を$a_{n,\mathrm{max}}$で表すと、次の式になります。
この操作はあくまで中間変数の値を小さくするもので、出力の値には影響しません。
・処理の確認
次に、バッチデータ対応版のソフトマックス関数の処理を確認します。
2次元配列(行列)の入力(この本では最終層の重み付き和)を作成します。
# (仮の)入力を作成 a = np.array([[0, 1, 2, 3, 4], [9, 8, 7, 6, 5], [10, 11, 12, -13, -14]]) print(a) print(a.shape)
[[ 0 1 2 3 4]
[ 9 8 7 6 5]
[ 10 11 12 -13 -14]]
(3, 5)
この例では、$(3 \times 5)$の2次元配列としました。これは、バッチサイズが3でクラス数が5であることを意味します。
データ(行)ごとに入力aの最大値を抽出します。
# 全ての要素から最大値を抽出 print(np.max(a)) # 1番目の軸ごとに最大値を抽出 print(np.max(a, axis=1))
12
[ 4 9 12]
ただし、3.5.1項のときのようにnp.max(a)とすると、aの全ての要素から最大値を抽出します。そこで、比較する軸を引数axisに指定します。axis=1を指定すると、1番目の軸の要素から最大値を抽出します。
この例だと、a.shapeの返り値が(3, 5)でした。つまりaは、「行数(0番目の軸の要素数)が3」、「列数(1番目の軸の要素数)が5」の配列です。axis=1を指定すると、1番目の軸(5個の要素)ごとに最大値を抽出します。よって、抽出した最大値は3個になります。
しかし、このままでは入力aから最大値を引けません。
# 入力から最大値を引く print(a - np.max(a, axis=1))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-18-586851da4078> in <module>
1 # 入力から最大値を引く
----> 2 print(a - np.max(a, axis=1))
ValueError: operands could not be broadcast together with shapes (3,5) (3,)
この処理は、aのデータ(行)ごとに、全てデータの最大値を引く計算をしています。aのデータ(行)ごとに、そのデータに関する最大値を引く必要があります。
ただし、行数と列数が同じ場合は計算できてしまいます。計算できてしまうと、ミスに気付けないので注意してください。
そこで、keepdims=Trueを指定して配列の次元数を維持します。
# 1番目の軸ごとに最大値を抽出 max_a = np.max(a, axis=1, keepdims=True) print(max_a) print(max_a.shape)
[[ 4]
[ 9]
[12]]
(3, 1)
軸の数が維持されています。これによって、aの各行とmax_aの各行の計算を行えます。
入力aから、最大値max_aを引きます。
# 行(データ)ごとに最大値を引く tmp_a = a - max_a print(a) print(tmp_a)
[[ 0 1 2 3 4]
[ 9 8 7 6 5]
[ 10 11 12 -13 -14]]
[[ -4 -3 -2 -1 0]
[ 0 -1 -2 -3 -4]
[ -2 -1 0 -25 -26]]
0行目の要素から4、1行目の要素から9、2行目の要素から12を引けています。よって、全ての要素が0以下の値になりました。
全ての要素の指数をとります。
# 分子の計算 exp_a = np.exp(tmp_a) print(np.round(exp_a, 3))
[[0.018 0.05 0.135 0.368 1. ]
[1. 0.368 0.135 0.05 0.018]
[0.135 0.368 1. 0. 0. ]]
これが分子の値です。
データ(行)ごとに総和を計算します。ここでも、軸の指定と軸の数の維持をする必要があります。
# 分母の計算 sum_exp_a = np.sum(exp_a, axis=1, keepdims=True) print(sum_exp_a)
[[1.57131743]
[1.57131743]
[1.50321472]]
これが分母の値です。
np.sum()についてもaxisとkeepdimsを指定しないと、np.max()のときと同じ問題が生じます。
# 全ての要素の和を計算 print(np.sum(exp_a)) # 1番目の軸の和を計算 print(np.sum(exp_a, axis=1))
4.6458495877563575
[1.57131743 1.57131743 1.50321472]
どちらの関数も、複数の要素を1つの要素に変換するため、配列の形状(軸の数)に影響します。
分子の値exp_aを分母の値sum_exp_aで割ります。
# 式(3.10)の計算 y = exp_a / sum_exp_a print(np.round(y, 3)) print(np.sum(y, axis=1))
[[0.012 0.032 0.086 0.234 0.636]
[0.636 0.234 0.086 0.032 0.012]
[0.09 0.245 0.665 0. 0. ]]
[1. 1. 1.]
全ての要素が0から1の値になりました。また、データ(行)ごとの和がになっています。これで2次元配列を処理できました。
以上が2次元配列に対するソフトマックス関数で行う処理です。
・実装
処理の確認ができたので、多次元配列対応版のソフトマックス関数(Softmax関数)を関数として実装します。
# ソフトマックス関数の実装 def softmax(x): # 最大値を引く:オーバーフロー対策 x = x - np.max(x, axis=-1, keepdims=True) # ソフトマックス関数の計算:(3.10) return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
中間変数(オブジェクト)を持たないように、先ほど確認した処理をまとめて計算しています。
また、軸の引数axisに-1を指定しています。-1は、最後の要素のインデックスを表します。よって3次元配列であれば、axis=-1はaxis=2を意味します。
例えば、(データ数, チャンネル数, クラス数)のような3次元配列の場合に、axis=-1を指定すると2番目(最後)の軸に格納されている「$K$個のクラスに対応した要素」に対して式(3.10)の計算をします(正規化します)。
これにより、2次元以上の多次元配列にも対応できます。
実装した関数を試してみましょう。
# (仮の)入力を作成 a = np.array([[0, 1, 2, 3, 4], [9, 8, 7, 6, 5], [10, 11, 12, -13, -14]]) print(a) # ソフトマックス関数による活性化(正規化) y = softmax(a) print(np.round(y, 3)) print(np.sum(y, axis=1))
[[ 0 1 2 3 4]
[ 9 8 7 6 5]
[ 10 11 12 -13 -14]]
[[0.012 0.032 0.086 0.234 0.636]
[0.636 0.234 0.086 0.032 0.012]
[0.09 0.245 0.665 0. 0. ]]
[1. 1. 1.]
# (仮の)入力を作成 a = np.array([[1010, 1000, 990], [1010, 1020, 1030], [1050, 1051, 1052]]) print(a) # ソフトマックス関数による活性化(正規化) y = softmax(a) print(np.round(y, 3)) print(np.sum(y, axis=1))
[[1010 1000 990]
[1010 1020 1030]
[1050 1051 1052]]
[[1. 0. 0. ]
[0. 0. 1. ]
[0.09 0.245 0.665]]
[1. 1. 1.]
# (仮の)入力を作成 a = np.array([-1.5, 1.0, 3.0]) print(a) # ソフトマックス関数による活性化(正規化) y = softmax(a) print(np.round(y, 3)) print(np.sum(y))
[-1.5 1. 3. ] [0.01 0.118 0.872] 1.0
オーバーフローも発生せずに正規化できています。この関数で、配列の形状に関わらず処理できます。
以上で、ソフトマックス関数を実装できました。次節では、学習済みのパラメータを用いて手書き文字認識を行います。
・グラフの確認
最後に、ソフトマックス関数をグラフで確認します。3Dプロットについては「3Dプロットの作図【ゼロつく1のノート(Python)】 - からっぽのしょこ」を参照してください。
・2クラスの場合
3次元のグラフで可視化するためにクラス数を2とします。
作図用と計算用の入力$\mathbf{x} = (x_0, x_1)$を作成します。
# 入力の値を作成 x_vals = np.arange(-5.0, 5.1, 0.5) # 作図用の入力を作成 X0_vals, X1_vals = np.meshgrid(x_vals, x_vals) # 計算用の入力を作成 X_vals = np.array([ X0_vals.flatten(), X1_vals.flatten() ]).T print(X_vals[:5]) print(X_vals.shape) # 作図用の入力の形状を保存 input_shape = X0_vals.shape print(input_shape)
[[-5. -5. ]
[-4.5 -5. ]
[-4. -5. ]
[-3.5 -5. ]
[-3. -5. ]]
(441, 2)
(21, 21)
$x_0$と$x_1$がとり得る値を作成してx_valsとします。
$x_0$と$x_1$がx_valsの全ての組み合わせを持つようにnp.meshgrid()で作成して、それぞれX0_valsとX1_valsとします。
X0_vals, X1_valsを1列に並び替えて結合してX_valsとします。各行が1つの点$\mathbf{x}$に対応します。
また、各入力$x_0, x_1$の元の形状をinput_shapeとして保存しておきます。
ソフトマックス関数の出力$\mathbf{y} = (y_0, y_1)$を計算します。
# ソフトマックス関数による活性化 Y_vals = softmax(X_vals) print(np.round(Y_vals[:5], 3)) print(np.sum(Y_vals[:5], axis=1))
[[0.5 0.5 ]
[0.622 0.378]
[0.731 0.269]
[0.818 0.182]
[0.881 0.119]]
[1. 1. 1. 1. 1.]
行(点)ごとの和が1になります。
$\mathbf{x}$と$y_0$のグラフを作成します。
# y0を整形 Y0_vals = np.array(Y_vals[:, 0]).reshape(input_shape) # xとy0のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, Y0_vals, label='$y_0$') # ワイヤーフレーム図 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('$y_0$') # z軸ラベル ax.set_title('Softmax Function', fontsize=20) # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
同様に、$\mathbf{x}$と$y_1$のグラフを作成します。
# y1を整形 Y1_vals = np.array(Y_vals[:, 1]).reshape(input_shape) # xとy1のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, Y1_vals, label='$y_1$') # ワイヤーフレーム図 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('$y_1$') # z軸ラベル ax.set_title('Softmax Function', fontsize=20) # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
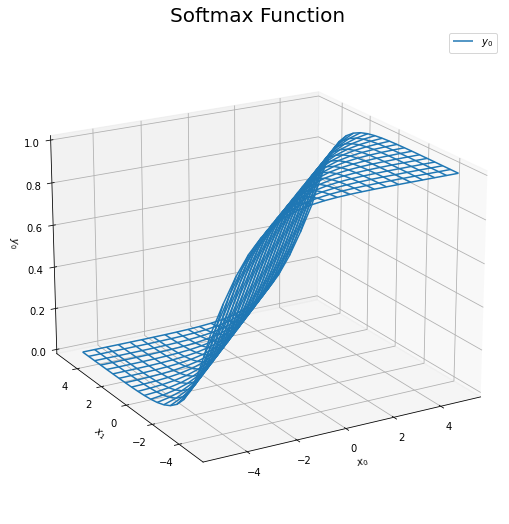

左の図は$y_0$のグラフです。$x_0 > x_1$となるほど$y_0$が大きくなるのが分かります。また、$0 < y_0 < 1$なのを認できます。
右の図は$y_1$のグラフです。左図と逆に、$x_0 < x_1$となるほど$y_1$が大きくなります。また、$0 < y_1 < 1$なのを確認できます。
続いて、$x_0$を固定した$\mathbf{x}$と$y_1$のグラフを確認します。
・コード(クリックで展開)
# 固定する値を指定 x0_list = [-5.0, -3.5, 0.0, 2.5, 4.0] # xとy1のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X0_vals, X1_vals, Y1_vals, label='$y_1$') # ワイヤーフレーム図 # 固定した値ごとにグラフを描画 for x0 in x0_list: # x0を固定した入力を作成 tmp_X_vals = np.array([np.repeat(x0, len(x_vals)), x_vals]).T # ソフトマックス関数による活性化 tmp_Y_vals = softmax(tmp_X_vals) tmp_y1_vals = np.array(tmp_Y_vals[:, 1]).flatten() # y1を整形 # x0を固定したy1のグラフを描画 ax.plot(np.repeat(x0, len(x_vals)), x_vals, tmp_y1_vals, linewidth=5, label='$x_0=' + str(x0) + '$') ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('$y_1$') # z軸ラベル ax.set_title('Softmax Function', fontsize=20) # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 #ax.view_init(elev=0, azim=0) # 表示アングル plt.show()

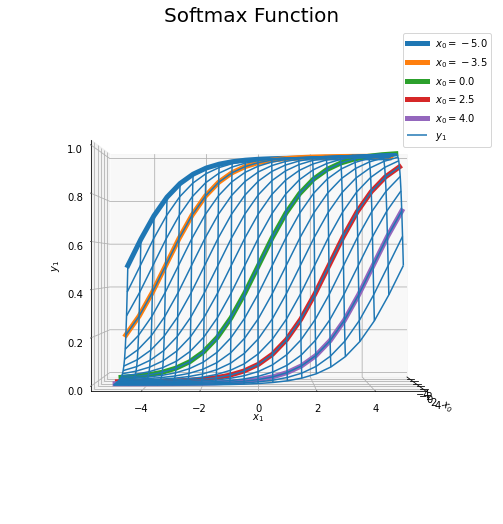
$x_0$を固定しているので、$x_1$方向に伸びる曲線になります。
$x_1$と$y_1$のグラフを確認します。
・コード(クリックで展開)
# x1とy1のグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 # 固定した値ごとにグラフを描画 for x0 in x0_list: # x0を固定した入力を作成 tmp_X_vals = np.array([np.repeat(x0, len(x_vals)), x_vals]).T # ソフトマックス関数による活性化 tmp_Y_vals = softmax(tmp_X_vals) tmp_y1_vals = np.array(tmp_Y_vals[:, 1]).flatten() # 出力を整形 # x0を固定したy1のグラフを描画 plt.plot(x_vals, tmp_y1_vals, label='$x_0=' + str(x0) + '$') plt.xlabel('$x_1$') # x軸ラベル plt.ylabel('$y_1$') # y軸ラベル plt.title('Softmax Function', fontsize=20) # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show() # グラフを表示
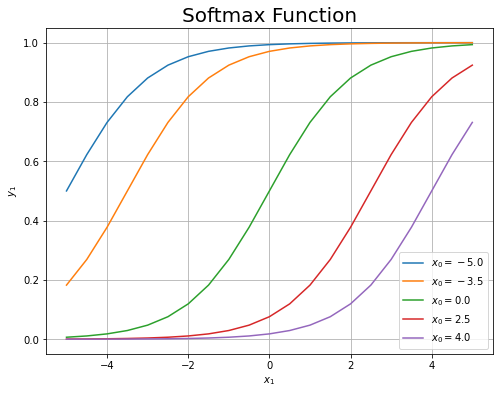
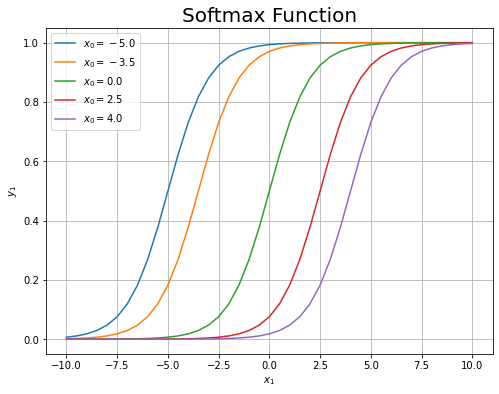
先ほどの3Dグラフを、それぞれ固定した$x_0$の値で切断した断面図に対応しています。
左は3Dグラフの表示範囲に対応しています。右は$x_1$方向の描画範囲を広げた図です。
どのグラフも同じ形をしているのが分かります。$x_0 = x_1$のとき$y_1 = 0.5$になるように$x_1$軸方向に移動しています。
$x_0$を固定した上で、$x_1$と$y_0, y_1$のグラフを作成します。
# 固定する値を指定 x0 = 2.5 # 作図用の入力の値を作成 x_vals = np.arange(-10.0, 10.1, 0.1) # 計算用のx0を固定した入力を作成 X_vals = np.array([ np.repeat(x0, len(x_vals)), x_vals ]).T # ソフトマックス関数による活性化 Y_vals = softmax(X_vals) # x1とy0,y1のグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 plt.plot(x_vals, np.array(Y_vals[:, 0]).flatten(), label='$y_0$') # y0のグラフ plt.plot(x_vals, np.array(Y_vals[:, 1]).flatten(), label='$y_1$') # y1のグラフ plt.xlabel('$x_1$') # x軸ラベル plt.ylabel('$y_k$') # z軸ラベル plt.suptitle('Softmax Function', fontsize=20) # 全体のタイトル plt.title('$x_0=' + str(x0) + '$', loc='left') # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
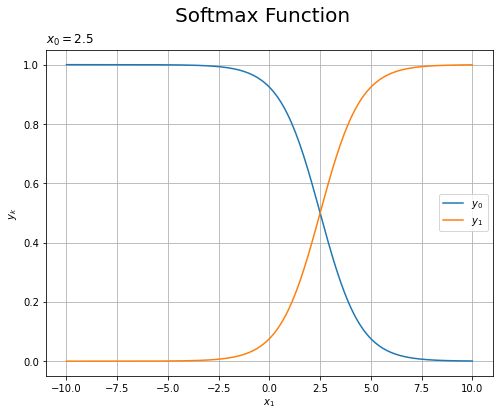
各$x_1$において$y_0 + y_1 = 1$になっているのが分かります。
$y_0$と$y_1$の3Dグラフ全体がこのような関係になっています。
ここまでは、2クラスの場合を確認しました。続いて、3クラスの場合を確認します。
・3クラスの場合
1つの変数を固定して疑似的な3クラスのソフトマックス関数を可視化します。
作図用と計算用の$\mathbf{x} = (x_0, x_1, x_2)$を作成します。ただし、$x_0$に関しては値を固定します。
# 固定する値を指定 x0 = 1.0 # 入力の値を作成 x_vals = np.arange(-10.0, 10.1, 0.5) # 作図用の入力を作成 X1_vals, X2_vals = np.meshgrid(x_vals, x_vals) # 計算用のx0を固定した入力を作成 X_vals = np.array([ np.repeat(x0, len(X1_vals.flatten())), X1_vals.flatten(), X2_vals.flatten() ]).T print(X_vals[:5]) print(X_vals.shape) # 作図用の入力の形状を保存 input_shape = X1_vals.shape print(input_shape)
[[ 1. -10. -10. ]
[ 1. -9.5 -10. ]
[ 1. -9. -10. ]
[ 1. -8.5 -10. ]
[ 1. -8. -10. ]]
(1681, 3)
(41, 41)
2変数のときと同様に、作図用の入力X1_vals, X2_valsと計算用の入力X_valsを作成します。
ただし、$x_0$をx0として値を指定しておき、X_valsの作成時にはnp.repeat()で値を複製します。各行が1つの点$\mathbf{x}$に対応します。
ソフトマックス関数の出力$\mathbf{y} = (y_0, y_1, y_2)$を計算します。
# ソフトマックス関数による活性化 Y_vals = softmax(X_vals) print(np.round(Y_vals[:5], 3)) print(np.sum(Y_vals[:5], axis=1))
[[1. 0. 0.]
[1. 0. 0.]
[1. 0. 0.]
[1. 0. 0.]
[1. 0. 0.]]
[1. 1. 1. 1. 1.]
行(点)ごとの和が1になります。
$x_1, x_2$と$y_0$のグラフを作成します。
# 出力を整形 Y0_vals = np.array(Y_vals[:, 0]).reshape(input_shape) # xとy0のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X1_vals, X2_vals, Y0_vals, label='$y_0$') # ワイヤーフレーム図 ax.set_xlabel('$x_1$') # x軸ラベル ax.set_ylabel('$x_2$') # y軸ラベル ax.set_zlabel('$y_0$') # z軸ラベル fig.suptitle('Softmax Function', fontsize=20) # 全体のタイトル ax.set_title('$x_0=' + str(x0) + '$', loc='left') # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
同様に、$x_1, x_2$と$y_1$、$x_1, x_2$と$y_2$のグラフを作成します。
・コード(クリックで展開)
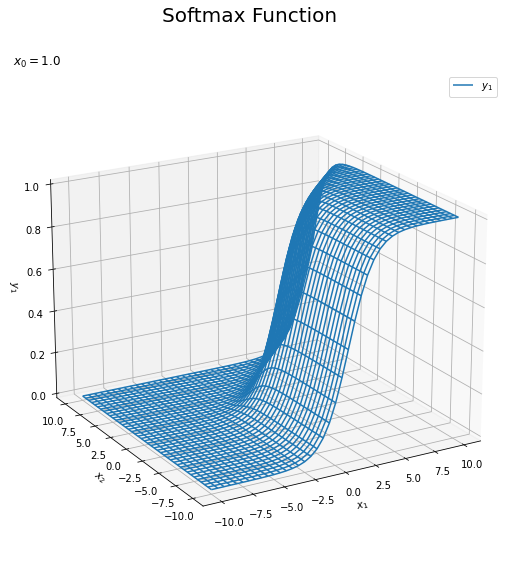
# y1を整形 Y1_vals = np.array(Y_vals[:, 1]).reshape(input_shape) # xとy1のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X1_vals, X2_vals, Y1_vals, label='$y_1$') # ワイヤーフレーム図 ax.set_xlabel('$x_1$') # x軸ラベル ax.set_ylabel('$x_2$') # y軸ラベル ax.set_zlabel('$y_1$') # z軸ラベル fig.suptitle('Softmax Function', fontsize=20) # 全体のタイトル ax.set_title('$x_0=' + str(x0) + '$', loc='left') # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
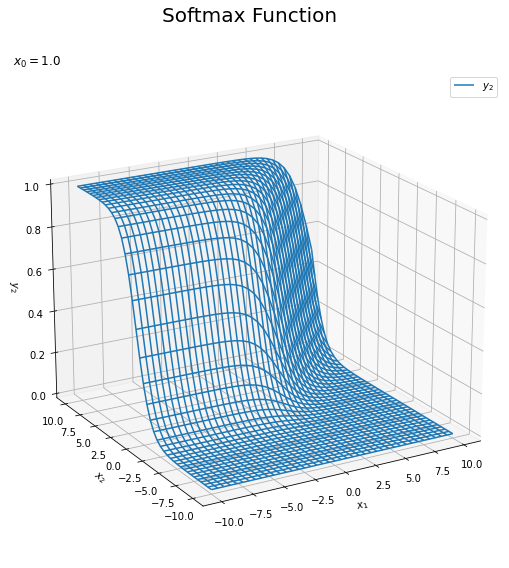
# y2を整形 Y2_vals = np.array(Y_vals[:, 2]).reshape(input_shape) # xとy2のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X1_vals, X2_vals, Y2_vals, label='$y_2$') # ワイヤーフレーム図 ax.set_xlabel('$x_1$') # x軸ラベル ax.set_ylabel('$x_2$') # y軸ラベル ax.set_zlabel('$y_2$') # z軸ラベル fig.suptitle('Softmax Function', fontsize=20) # 全体のタイトル ax.set_title('$x_0=' + str(x0) + '$', loc='left') # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 ax.view_init(elev=20, azim=240) # 表示アングル plt.show()
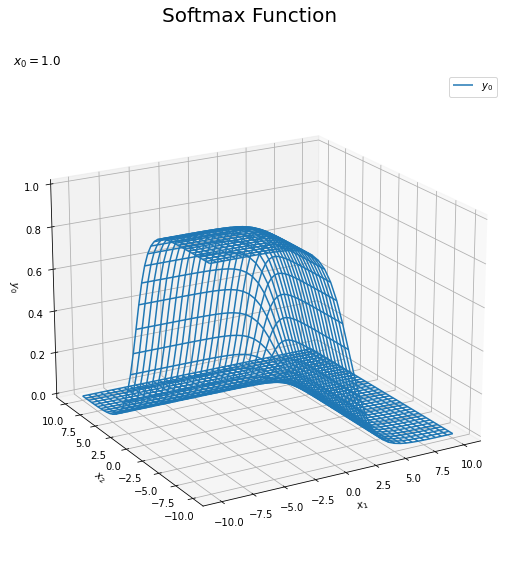
1つ目の図は$y_0$のグラフです。$x_1$と$x_2$の値が小さいほど$y_0$が大きくなるのが分かります。また、$0 < y_1 < 1$なのを確認できます。
2つ目と3つ目の図はそれぞれ$y_1, y_2$のグラフです。$x_1$が大きいほど$y_1$が大きくなり、$x_2$が大きいほど$y_2$が大きくなるのが分かります。
続いて、$x_0$と$x_1$を固定した$x_1, x_2$と$y_1$のグラフを確認します。
・コード(クリックで展開)
# 固定する値を指定 x1_list = [-5.0, -3.5, 0.0, 2.5, 4.0] # xとy2のグラフを作成 fig = plt.figure(figsize=(9, 9)) # 図の設定 ax = fig.add_subplot(projection='3d') # 3D用の設定 ax.plot_wireframe(X1_vals, X2_vals, Y2_vals, label='$y_2$') # ワイヤーフレーム図 # 固定した値ごとにグラフを描画 for x1 in x1_list: # x0,x1を固定した入力を作成 tmp_X_vals = np.array([np.repeat(x0, len(x_vals)), np.repeat(x1, len(x_vals)), x_vals]).T # ソフトマックス関数による活性化 tmp_Y_vals = softmax(tmp_X_vals) tmp_y2_vals = np.array(tmp_Y_vals[:, 2]).flatten() # 出力を整形 # x0,x1を固定したy2のグラフを描画 ax.plot(np.repeat(x1, len(x_vals)), x_vals, tmp_y2_vals, linewidth=5, label='$x_1=' + str(x1) + '$') ax.set_xlabel('$x_1$') # x軸ラベル ax.set_ylabel('$x_2$') # y軸ラベル ax.set_zlabel('$y_2$') # z軸ラベル fig.suptitle('Softmax Function', fontsize=20) # 全体のタイトル ax.set_title('$x_0=' + str(x0) + '$', loc='left') # タイトル ax.legend() # 凡例 ax.set_zlim(0, 1) # z軸の表示範囲 #ax.view_init(elev=0, azim=0) # 表示アングル plt.show()
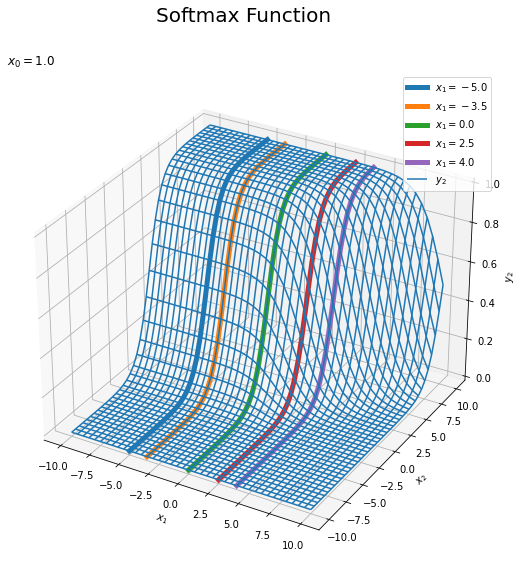
$x_0, x_1$を固定しているので、$x_2$方向に伸びる曲線になります。
$x_2$と$y_2$のグラフを確認します。
・コード(クリックで展開)
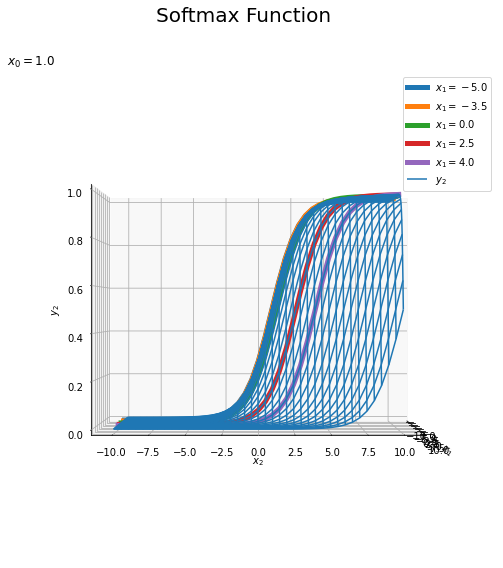
# x2とy2のグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 # 固定した値ごとにグラフを描画 for x1 in x1_list: # x0,x1を固定した入力を作成 tmp_X_vals = np.array([np.repeat(x0, len(x_vals)), np.repeat(x1, len(x_vals)), x_vals]).T # ソフトマックス関数による活性化 tmp_Y_vals = softmax(tmp_X_vals) tmp_y2_vals = np.array(tmp_Y_vals[:, 2]).flatten() # 出力を整形 # x0,x1を固定したy2のグラフを描画 plt.plot(x_vals, tmp_y2_vals, label='$x_1=' + str(x1) + '$') plt.xlabel('$x_2$') # x軸ラベル plt.ylabel('$y_2$') # z軸ラベル plt.suptitle('Softmax Function', fontsize=20) # 全体のタイトル plt.title('$x_0=' + str(x0) + '$', loc='left') # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
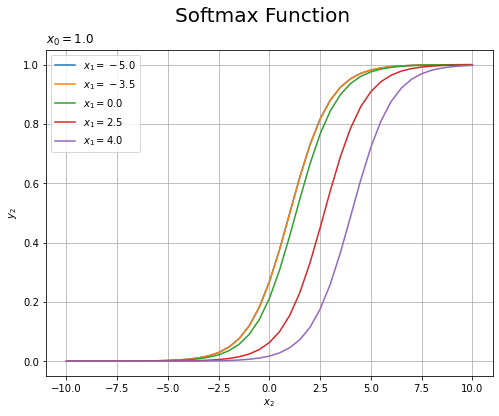
それぞれ固定した$x_1$の値で先ほどの3Dグラフを切断した断面図に対応しています。
どのグラフも同じ形をしており、$\exp(x_0) + \exp(x_1) = \exp(x_2)$のとき$y_2 = 0.5$になるように$x_2$軸方向に移動しています。
$x_0, x_1$を固定した上で、$x_2$と$y_0, y_1, y_2$のグラフを作成します。
# 固定する値を指定 x0 = 1.0 x1 = 2.5 # 作図用の入力の値を作成 x_vals = np.arange(-10.0, 10.1, 0.5) # 計算用のx0,x1を固定した入力を作成 X_vals = np.array([ np.repeat(x0, len(x_vals)), np.repeat(x1, len(x_vals)), x_vals ]).T # ソフトマックス関数による活性化 Y_vals = softmax(X_vals) # x2とy0,y1,y2のグラフを作成 plt.figure(figsize=(8, 6)) # 図の設定 for k in range(3): tmp_y_vals = np.array(Y_vals[:, k]).flatten() # 出力を整形 plt.plot(x_vals, tmp_y_vals, label='$y_' + str(k) + '$') # 折れ線グラフ plt.xlabel('$x_2$') # x軸ラベル plt.ylabel('$y_k$') # z軸ラベル plt.suptitle('Softmax Function', fontsize=20) # 全体のタイトル plt.title('$x_0=' + str(x0) + ', x_1=' + str(x1) + '$', loc='left') # タイトル plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()

各$x_2$において$y_0 + y_1 + y_2 = 1$になっているのが分かります。
$y_0, y_1, y_2$の3Dグラフ全体がこのような関係になっています。
以上で、ソフトマックス関数を実装できました。次節では、学習済みのパラメータを用いて手書き文字認識を行います。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
- サポートページ:ソフトマックス関数のコード(https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/common/functions.py)
おわりに
Jupyter Labでの資料作りも大変ではあるのですが、はてなに転載する作業も中々しんどいものがあります、、、何よりこの作業に手を取られて、そもそもの資料の続きを書けてません。。3章関連の記事はあと3つ!
- 2021.07.26:加筆修正しました。
この節で実装した関数だとバッチデータを処理できないことに後々気付いたので、その内容を書き足しました。それ以外にも細々と解説を加えていったら文字数が3倍になってしまいました。文量が多くなるのはもう気にしないことにしたので、頑張って読んでください。
ここからは、「ある関数の出力」とそれを「入力する関数」という話が増えていきます。何かの出力は、何かの入力なわけです。そのため、どの関数の入力・出力なのかを意識していないと話がこんがらがってきます。
なのでこのブログでは、何の出力でありまた何の入力なのかを丁寧に書くようにしています。ただ、丁寧に書くと分かりやすくなるかと言うとそうでもなくて、いちいち「○○の入力(または)出力の(それを表す)記号」と書いてると文字数が増えてそれはそれで分かりにくくなります。それでも個人的には「書いてなくて分からない」より「書いてあって分かりにくい」の方がいいと思っているので、お付き合いください。
記号をまとめた表とページを作って対応しようとも思ったのですが、微妙に表記が揺れるんですよね。表記ゆれとは別に、どの関数であっても、その関数の入力をxで出力をyで書きますし。
あと、ブログという形態だと1つの記事で完結していないと読みにくですしね。どうしたものか。
- 2021.09.14:グラフを追加しました。
思っていたより大変だった。というか2クラスのグラフを2枚作るだけのつもりだったのに、どうしてこうなった。
【次節の内容】
【関連する記事】