はじめに
『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでの実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。
この記事は、9.3.3項の内容です。混合ベルヌーイ分布に対するEMアルゴリズムによる最尤推定をPythonで実装します。
【数理編】
【他の節一覧】
【この節の内容】
・Pythonで実装
MNISTデータセットを用いて、混合ベルヌーイ分布に対する最尤推定(EMアルゴリズム)を行ってみましょう。
次のライブラリを利用します。
# 9.3.3項で利用するライブラリ import numpy as np #from scipy.stats import multinomial # 多項分布 import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
カテゴリ分布の確率の計算にSciPyのmultinomialクラスを利用することもできます。
この記事では、『ゼロから作るDeep Learning 3』のモジュールを利用してMNISTデータセットを取得します。
# ゼロつく3のモジュールを利用 import sys sys.path.append('パスを指定/deep-learning-from-scratch-3-master') from dezero.datasets import MNIST
えっと、ゼロつく3巻を参照するかそれぞれデータを用意してください、、、
・MNISTデータセットの準備
MNISTデータセットを取得して、利用するデータを作成します。
DeZeroのMNISTクラスのインスタンスを作成します。詳しくは、「ステップ51:MNISTデータセットの学習【ゼロつく3のノート(実装)】 - からっぽのしょこ」を参照してください。
# 訓練データを取得 train_set = MNIST(train=True) # 入力データ・教師データを取得 train_x = train_set.data.reshape((60000, 28**2)) / 255 # 前処理 train_t = train_set.label print(train_x.shape) print(train_t.shape)
(60000, 784)
(60000,)
「縦28・横28ピクセルの手書き文字の画像データ」と「書かれている数字を示すラベルデータ」のセットが6万枚分あります。それぞれ入力データと教師データと呼び、xとtで表すことにします。
入力データxの各要素(ピクセル)は0から255の値をとり、0は真っ黒で255は真っ白を表します。2次元配列のピクセルデータを1次元配列に並び替えて、また最大値の255で割ることで0から1の値になるように前処理しています。
教師データtは0から9の値をとり、10種類の数字を表します。
入力データ(の一部)と教師データを確認します。
# データを確認 print(train_x[:5, 205:210]) print(train_t[:5])
[[0.99215686 0.99215686 0.99215686 0.99215686 0.99215686]
[0. 0. 0.03921569 0.23529412 0.87843137]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0.21568627 0.58039216]]
[5 0 4 1 9]
(画像の隅は0が多いので適当に中の要素を出力しています。)
手書き文字をヒートマップとして作図して確認します。
# 表示するデータ番号を指定 n = 0 # 手書き文字を表示:(256段階) plt.imshow(train_x[n].reshape((28, 28)), cmap='gray') #plt.imshow(train_x[n].reshape((1, 28**2)), cmap='gray') plt.title('label:' + str(train_t[n])) plt.axis('off') # 軸ラベル plt.show()

この手書き文字を入力します。

ただしこの例では、全てのピクセルを1次元に並び替えて入力します。
MNISTデータセットを用意できました。次は、入力するデータを用意します。以降は共通する処理だと思います(?)。
ここでは、データセットの一部のみを利用することにします。目的に応じて次の2つの方法でデータを抽出します。
1つ目は、「データ数」を指定して全ての数字のデータをランダムに抽出します。
# データ数を指定 N = 10000 # クラス数の設定:(固定) K = 10 # シャッフルして指定した数のデータを抽出 idx = np.random.permutation(len(train_x))[:N] x_nd = train_x[idx] t_n = train_t[idx] print(x_nd.shape) print(t_n.shape) print(t_n[:10])
(10000, 784)
(10000,)
[3 6 1 3 4 0 3 7 0 5]
データ数$N$を指定して、データを取り出します。
入力データ$\mathbf{X} = (\mathbf{x}_0, \mathbf{x}_1, \cdots, \mathbf{x}_{N-1})$、$\mathbf{x}_n = (x_{n0}, x_{n1}, \cdots, x_{nD-1})$、$0 \leq x_{nd} \leq 1$をx_nd、教師データ$\mathbf{t} = (t_0, t_1, \cdots, t_{N-1})$、$t_n \in \{0, 1, \cdots, 9\}$をt_nとします。全ての数字を利用するので、クラス数$K$は10です。また、入力データ$\mathbf{x}_n$の次元数$D$は$28 \times 28 = 784$です。
np.random.permutation()を使って、データセットのインデックスに対応した整数をランダムに生成して、N個取り出します。取り出したN個の値を添字として利用して、入力データと教師データを抽出します。
2つ目は、「データ数」と「利用する数字」を指定してデータをランダムに抽出します。
# データ数を指定 N = 5000 # クラスを指定 label_list = [2, 4, 6, 8] # クラス数を設定 K = len(label_list) # 指定したクラスのデータを抽出 x_arr = np.empty((0, 784)) t_arr = np.empty(0) for k in range(K): # クラスkのデータを抽出 x_arr = np.append(x_arr, train_x[train_t == label_list[k]], axis=0) t_arr = np.append(t_arr, train_t[train_t == label_list[k]], axis=0) # 指定した数のデータをランダムに抽出 idx = np.random.permutation(len(x_arr))[:N] # 抽出するデータ番号 x_nd = x_arr[idx] t_n = t_arr[idx].astype('int') print(x_nd.shape) print(t_n.shape) print(t_n[:10])
(5000, 784)
(5000,)
[2 2 2 8 4 8 6 8 2 2]
データ数をN、利用(入力)する数字をlabel_listに指定して、データを取り出します(もっと上手いやり方があれば教えて下さい)。クラス数$K$は、指定した数字の数とします。
train_x, train_tからlabel_listに指定した数字のデータを取り出して、x_arr, t_arrに格納していきます。その後に、先ほどと同様に指定したデータ数をランダムに抽出します。
MNISTデータセットから利用するデータを抽出できました。続いて、混合ベルヌーイモデルに対応したデータに変換します。
混合ベルヌーイモデルでは、「入力データの各要素$x_{nd}$」は「入力データのクラス$k$のパラメータ$\mu_{kd}$」を持つベルヌーイ分布$p(x_{nd} | \mu_{kd})$から生成されているとします。
ベルヌーイ分布に従う変数は0か1の2値をとる$x_{nd} \in \{0, 1\}$ため、x_ndの要素を0か1に変換する必要があります。($n$番目の入力データ$\mathbf{x}_n$のクラスが$k$であることを$z_{nk} = 1$で表しますが、ここでは(オブジェクトとして)登場しないので省略します。)
この例だと次のようになります。
・長いので省略(クリックで展開)
$n$番目の手書き文字(入力データ)$\mathbf{x}_n$は、要素数が$D = 784$のベクトル(1次元配列)です。$\mathbf{x}_n$に書かれている数字(正解ラベル)が$k$だとします。$k$を真のクラスと呼ぶことにします。クラス$k$のときのパラメータは$\boldsymbol{\mu}_k$です。$\mathbf{x}_n$の各要素(ピクセル)$x_{nd}$は、対応するパラメータ$\mu_{kd}$に従って、値が0か1に決まると仮定しています。$d$はピクセルの位置を表します。$x_{nd}$の値が0のとき、位置$d$のピクセルは書かれていない(黒である)ことを表します。逆に、$x_{nd} = 1$であれば、そのピクセルは書かれている(白である)ことを表します。
例えば、書かれている数字が1であれば、真ん中の縦一線のピクセルが書かれ(白になり)ますね。人によって位置が微妙にズレますが、大体は真ん中で縦に並ぶピクセルになりそうです。書かれている可能性の高さを、パラメータの値が大きい(1に近い)ことで表現できます。逆に、ほとんど書かれない隅のパラメータは、値が小さく(0に近く)なります。
また、別の文字では傾向が異なりますね。これを、クラスごとにパラメータが異なることで表現(モデルを仮定)します。
つまり、1つの入力データ$\mathbf{x}_n$は、$D$個の0か1の要素の組み合わせ(同時分布)と言えます。ただし、各要素は独立に生成されていると仮定します。よって、$\mathbf{x}_n$のクラスが$k$のとき、$D$個のベルヌーイ分布の積で表現します。
また、$K$個全てのクラスを考慮すると、混合ベルヌーイ分布で表現します。
要素ごと$x_{nd}$ではなく、データごと$\mathbf{x}_n$に1つのクラスを持ちます。パラメータについては、初期値の設定のところでもう少し確認します。
さて、話をプログラムに戻します。
入力データ$\mathbf{X}$を0か1をとる2値変数に変換します。ここでは、x_ndの値が0.5より大きいと1、以下だと0とすることにします。
# 2値に変換 x_nd = (x_nd > 0.5).astype('int') # データを確認 print(x_nd[:5, 150:160])
[[0 0 0 0 0 0 0 0 0 0]
[1 1 1 0 0 0 0 0 0 0]
[0 1 1 1 1 1 0 0 0 0]
[0 0 0 0 0 1 1 1 1 0]
[0 0 0 1 1 0 0 0 0 0]]
x_nd > 0.5とすると各要素が条件に従ってTrueとFalseになります。さらに、asdtype()を使って整数型intに変換します。Trueは1、Falseは0になります。
変換した入力データ(手書き文字)も確認しましょう。
# 表示するデータ番号を指定 n = 0 # 手書き文字を表示:(2値) plt.imshow(x_nd[n].reshape((28, 28)), cmap='gray') plt.title('label:' + str(t_n[n])) plt.axis('off') # 軸ラベル plt.show()

黒と白の2色になります。(この記事では分かりやすいように先ほどと同じデータを表示していますが、ランダムに抽出した後なので同じデータにはなりません。)
以上でMNISTデータセットの確認と入力データの作成は完了です。次は、学習に関する処理を行っていきます。
・初期値の設定
パラメータの初期値を生成します。
# 次元数を設定:(固定) D = 784 # モデルのパラメータを初期化 mu_kd = np.random.uniform(low=0.25, high=0.75, size=(K, D)) # 混合係数を初期化 pi_k = np.repeat(1.0 / K, K) # 負担率の変数を作成 gamma_nk = np.zeros((N, K))
入力データ$\mathbf{x}_n$の次元数$D$は$28 \times 28 = 784$です。
モデルのパラメータ$\boldsymbol{\mu} = (\boldsymbol{\mu}_0, \boldsymbol{\mu}_1, \cdots, \boldsymbol{\mu}_{K-1})$、$\boldsymbol{\mu}_k = (\mu_{k0}, \mu_{k1}, \cdots, \mu_{kD-1})$、$0 \leq \mu_{kd} \leq 1$は、$K \times D$の2次元配列mu_kdとします。初期値は0.25から0.75の一様分布に従って生成します。$\mu_{kd}$は、$\mathbf{x}_n$のクラスを$k$としたとき、$x_{nd}$が1になる確率を表します。$1 - \mu_{kd}$は、$x_{nd}$が0になる確率と言えます。
混合係数$\boldsymbol{\pi} = (\pi_0, \pi_1, \cdots, \pi_{K-1})$、$0 \leq \pi_k \leq 1$、$\sum_{k=0}^{K-1} \pi_k = 1$は、要素数$K$の1次元配列pi_kとします。初期値は$\frac{1}{K}$とします。$\pi_k$は、各入力データのクラスが$k$である確率を表します。
負担率$\gamma(\mathbf{Z})$は初期値を持ちませんが、添字を指定して代入していくために、$N \times K$の2次元配列gamma_nkを作成しておきます。
・推論処理
続いて、学習を行います。最尤推定では、EステップとMステップを交互に繰り返します。Eステップでは、負担率$\gamma(\mathbf{Z})$を更新します。Mステップでは、対数尤度が最大化されるようにパラメータ$\boldsymbol{\mu},\ \boldsymbol{\pi}$を更新します。
まずは、パラメータの初期値を用いて負担率を更新します。続いて、更新した負担率を用いて各パラメータを更新します。ここまでが1回の試行です。
次の試行では、前回更新したパラメータを用いて負担率を更新となります。この処理を指定した回数繰り返します。
・コード全体
後でパラメータの更新値や推論結果の推移を確認するために、リストtrace_***に値を格納しておきます。
# 試行回数を指定 MaxIter = 100 # 推移の確認用の受け皿を作成 trace_L_i = [] trace_mu_ikd = [mu_kd.copy()] trace_pi_ik = [pi_k.copy()] trace_gamma_ink = [] # 最尤推定 for i in range(MaxIter): # 負担率を計算:式(9.56) for n in range(N): for k in range(K): prob_x_d = np.c_[1.0 - mu_kd[k], mu_kd[k]][np.arange(D), x_nd[n]] # D個のベルヌーイ分布 #prob_x_d = multinomial.pmf(x=np.c_[x_nd[n], 1 - x_nd[n]], n=1, p=np.c_[mu_kd[k], 1 - mu_kd[k]]) # (SciPy) gamma_nk[n, k] = pi_k[k] * np.prod(prob_x_d) # 分子 gamma_nk /= np.sum(gamma_nk, axis=1, keepdims=True) # 正規化 # 各クラスタとなるデータ数の期待値を計算:式(9.57) N_k = np.sum(gamma_nk, axis=0) # モデルのパラメータの最尤解を計算:式(9.59) mu_kd = np.dot(gamma_nk.T, x_nd) / N_k.reshape((K, 1)) # 混合係数の最尤解を計算:式(9.60) pi_k = N_k / N # 不完全データ対数尤度を計算:式(9.51) prob_mix_n = np.zeros(N) for n in range(N): for k in range(K): prob_x_d = np.c_[1.0 - mu_kd[k], mu_kd[k]][np.arange(D), x_nd[n]] # D個のベルヌーイ分布 #prob_x_d = multinomial.pmf(x=np.c_[x_nd[n], 1 - x_nd[n]], n=1, p=np.c_[mu_kd[k], 1 - mu_kd[k]]) # (SciPy) prob_mix_n[n] += pi_k[k] * np.prod(prob_x_d) # 混合ベルヌーイ分布 L = np.sum(np.log(prob_mix_n)) # i回目の結果を記録 trace_L_i.append(L) trace_mu_ikd.append(mu_kd.copy()) trace_pi_ik.append(pi_k.copy()) trace_gamma_ink.append(gamma_nk.copy()) # 動作確認 print(str(i + 1) + ' (' + str(np.round((i + 1) / MaxIter * 100, 1)) + '%)')
(結構時間がかかりました。)
・処理の解説
続いて、EMアルゴリズムで行う処理を確認していきます。
・Eステップ
Eステップでは、負担率を更新します。
前回のパラメータを用いて、負担率を更新します。
# 負担率を計算:式(9.56) for n in range(N): for k in range(K): prob_x_d = np.c_[1.0 - mu_kd[k], mu_kd[k]][np.arange(D), x_nd[n]] # D個のベルヌーイ分布 #prob_x_d = multinomial.pmf(x=np.c_[x_nd[n], 1 - x_nd[n]], n=1, p=np.c_[mu_kd[k], 1 - mu_kd[k]]) # (SciPy) gamma_nk[n, k] = pi_k[k] * np.prod(prob_x_d) # 分子 gamma_nk /= np.sum(gamma_nk, axis=1, keepdims=True) # 正規化
負担率は、次の式で計算します。
prob_x_dは、$D$個のベルヌーイ分布の計算結果です。$\mathrm{Bern}(x_{nd} | \mu_{kd})$は、$x_{nd} = 1$のとき$\mu_{nk}$で、$x_{nd} = 0$のとき$1 - \mu_{nk}$です。そこで、クラスkに関して、1 - mu_kd[k]列とmu_kd[k]列からなるD行の2次元配列を作り、x_nd[n]を添字とすることで、対応するパラメータを抽出しています。SciPyの多項分布の確率関数multinomial.pmf()を使って計算することもできます。
クラスkのD個のパラメータの積np.prod(prod_x_d)と混合比率pi_k[k]の積が、式(9.56)の分子であり、正規化前の負担率です。
全ての要素を更新できたら、行ごとの和で割り正規化します。
$\gamma(z_{nk})$は、「各ピクセル$x_{nd}$において、1であれば$\mu_{kd}$、0であれば$1 - \mu_{kd}$」とした$D$個のパラメータの積を、$\pi_k$で割り引いた値によって決まるのが式から分かります。分母は、$\gamma(z_{nk})$が$0 \leq \gamma(z_{nk}),\ \sum_{k=0}^{K-1} \gamma(z_{nk}) = 1$となるための正規化項です。
また、クラス$k$において、$\mu_{kd}$は$x_{nd} = 1$となる確率、$1 - \mu_{kd}$は$x_{nd} = 0$となる確率を表すのでした。これは、$x_{nd} = 1$となる可能性が高いほど$\mu_{kd}$が1に近く($1 - \mu_{kd}$が0に近く)なり、$x_{nd} = 0$となる可能性が高いほど$\mu_{kd}$が0に近く($1 - \mu_{kd}$が1に近く)なることで、クラス$k$の特徴を表していると言えます。
つまり、$\mathbf{x}_n$が、クラス$k$の特徴$\boldsymbol{\mu}_k$に近いほど$\gamma(z_{nk})$の値が大きく($\mathbf{x}_n$のクラスが$k$である確率が高く)なり、遠いほど$\gamma(z_{nk})$の値が小さく($\mathbf{x}_n$のクラスが$k$である確率が低く)なります。
計算結果は次のようになります。
# 確認 print(np.round(gamma_nk, 3)) print(np.sum(gamma_nk, axis=1))
[[0. 0. 0. ... 0. 0. 0.]
[1. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
...
[0. 0. 1. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 1.]
[0. 0. 0. ... 0. 1. 0.]]
[1. 1. 1. ... 1. 1. 1.]
この結果は最後の更新値です。データ(行)ごとに(概ね)1つのクラスに収束しています。そのクラスに分類(クラスタリング)されたと言えます。
負担率を用いて、各クラスに分類されるデータ数の期待値を計算します。
# 各クラスタとなるデータ数の期待値を計算:式(9.57) N_k = np.sum(gamma_nk, axis=0)
負担率は、各データがどのクラスなのかを確率で表したものです。クラスごとに全てのデータの確率を足しています。
# 確認 print(np.round(N_k, 1)) print(np.sum(N))
[ 408.2 627.4 1091.6 1220.7 1180.5 850. 771.3 1564.3 1360.8 925.1]
10000
$N_k$の総和は、データ数$N$になります。$N_k$は、パラメータの計算に利用します。
・Mステップ
Mステップでは、対数尤度を最大にするパラメータを更新(最尤解を計算)します。
モデルのパラメータを更新します。
# モデルのパラメータの最尤解を計算:式(9.59) mu_kd = np.dot(gamma_nk.T, x_nd) / N_k.reshape((K, 1))
各クラスのパラメータ$\boldsymbol{\mu}_k$は、次の式で計算します。
ただし、$\sum_{n=1}^N \gamma(z_{nk}) x_{nd}$が$\gamma(\mathbf{z}_n)$と$\mathbf{x}_n$の内積$\gamma(\mathbf{z}_n)^{\top} \mathbf{x}_n$であることから、$\gamma(\mathbf{Z})^{\top} \mathbf{X}$の計算をすることで一度に処理しています。
1つの要素$\mu_{kd}$に注目すると次の式になります。
$\gamma(z_{nk})$は$n$番目のデータがクラス$k$である確率、$x_{nd}$は$n$番目のデータの$d$番目のピクセルで、0か1の値をとるのでした。また、$\mu_{kd}$はクラス$k$において各データの$d$番目のピクセルが1である確率を表します。
各パラメータ$\mu_{kd}$は、「$\mu_{kd}$に対応するピクセル$x_{nd}$が1であるデータの負担率$\gamma(z_{nk})$」の総和によって決まるのが式から分かります。また、全てのデータの$d$番目のピクセルが、0のとき$\sum_{n=1}^N \gamma(z_{nk}) x_{nd} = 0$となり、1のとき$\sum_{n=1}^N \gamma(z_{nk}) x_{nd} = N_k$となります。よって、$N_k$は、$\mu_{kd}$が0から1の値になるように調整する働きがあります。
つまり、$d$番目のピクセルが1のデータが多いほど$\mu_{kd}$が大きくなります。
# 確認 print(np.round(mu_kd[:5, 100:110], 3))
[[0.283 0.153 0.065 0.025 0. 0. 0. 0. 0. 0. ]
[0.336 0.394 0.388 0.3 0.199 0.104 0.041 0.016 0.005 0.002]
[0.005 0.005 0.002 0.002 0. 0.001 0. 0. 0. 0. ]
[0. 0. 0.001 0.001 0. 0. 0. 0. 0. 0. ]
[0.008 0.007 0.004 0.005 0.003 0.002 0.001 0. 0. 0. ]]
0から1の値になります。
混合係数を更新します。
# 混合係数の最尤解を計算:式(9.60)
pi_k = N_k / N
混合比率の各要素$\pi_k$は、次の式で計算します。
各クラスとなるデータ数の期待値が、全体に占める割合です。
# 確認 print(np.round(pi_k, 3)) print(np.sum(pi_k))
[0.041 0.063 0.109 0.122 0.118 0.085 0.077 0.156 0.136 0.093]
0.9999999999999996
和が1になります。
・対数尤度の計算
最後に、更新したパラメータを用いて、対数尤度を計算します。
# 不完全データ対数尤度を計算:式(9.51) prob_mix_n = np.zeros(N) for n in range(N): for k in range(K): prob_x_d = np.c_[1.0 - mu_kd[k], mu_kd[k]][np.arange(D), x_nd[n]] # D個のベルヌーイ分布 #prob_x_d = multinomial.pmf(x=np.c_[x_nd[n], 1 - x_nd[n]], n=1, p=np.c_[mu_kd[k], 1 - mu_kd[k]]) # (SciPy) prob_mix_n[n] += pi_k[k] * np.prod(prob_x_d) # 混合ベルヌーイ分布 L = np.sum(np.log(prob_mix_n))
(不完全データ)対数尤度は、次の式で計算します。
負担率のときと同様に、$D$個のベルヌーイ分布の確率(パラメータ)をprob_x_dとして、その積を混合係数で加重平均をとった値が混合ベルヌーイ分布の確率prob_mix_n[n]です。これを全てのデータで求めて、対数をとった総和が対数尤度です。
以上が、EMアルゴリズムで行う個々の処理です。この処理を指定した回数繰り返します。
・推論結果の確認
推論結果を確認していきます。
・パラメータの確認
最終的なモデルのパラメータ$\boldsymbol{\mu}$を確認していきます。資料作成上の都合で、ここまでの結果と以降の結果は別のものです。
$k$番目のパラメータ$\boldsymbol{\mu}_k$を可視化します。
# 表示するクラス番号を指定 k = 0 # クラスkのパラメータを表示 plt.imshow(mu_kd[k].reshape((28, 28)), cmap='gray') plt.title('k=' + str(k)) plt.axis('off') # 軸ラベル plt.show()

入力データのときと同様に、k番目のパラメータmu_kd[k]をヒートマップにします。クラス番号はランダムに決まるので、元のラベル番号とは一致しません。
$K$個のパラメータをまとめて表示します。
# サブプロットの列数を指定(1行になるとエラーになる) n_col = 4 n_row = K // (n_col + 1) + 1 # モデルのパラメータをまとめて表示 fig, axes = plt.subplots(n_row, n_col, figsize=(8, 7), constrained_layout=True) for k in range(K): # サブプロットのインデックスを計算 r = k // n_col c = k % n_col # クラスkのパラメータ axes[r, c].imshow(mu_kd[k].reshape((28, 28)), cmap='gray') axes[r, c].axis('off') axes[r, c].set_title('k=' + str(k)) # 余ったサブプロットを初期化 for c in range(c + 1, n_col): axes[r, c].axis('off') # 最後のサブプロットにパラメータの平均値を表示 axes[r, n_col - 1].imshow(mu_kd.mean(axis=0).reshape((28, 28)), cmap='gray') axes[r, n_col - 1].set_title('iter:' + str(MaxIter) + ', N=' + str(N) + '\n (mean)') fig.suptitle('EM Algorithm', fontsize=20) # グラフタイトル plt.show()
n_colにサブプロットの列数を指定して、行数n_rowを計算します。ただし、行数が1のときは、axes[c]とする必要がありaxes[r, c]がエラーになります。また最後に、平均値を表示するので、設定の仕方を調整してください。(自動でいい感じするようにしたかった)

重複していたり、複数の数字が合わさったような状態になったりすることもあります。
更新値の推移をアニメーションで確認します。
・コード(クリックで展開)
# 画像サイズを指定 fig, axes = plt.subplots(n_row, n_col, figsize=(8, 7), constrained_layout=True) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目のパラメータをまとめて表示 for k in range(K): # サブプロットのインデックスを計算 r = k // n_col c = k % n_col # クラスkのパラメータ axes[r, c].imshow(trace_mu_ikd[i][k].reshape((28, 28)), cmap='gray') axes[r, c].axis('off') # 余ったサブプロットを初期化 for c in range(c + 1, n_col): axes[r, c].cla() axes[r, c].axis('off') # 最後のサブプロットにパラメータの平均値を表示 axes[r, n_col - 1].imshow(trace_mu_ikd[i].mean(axis=0).reshape((28, 28)), cmap='gray') axes[r, n_col - 1].set_title('mean') # 最初のサブプロットのタイトルに試行回数を表示 axes[0, 0].set_title('iter:' + str(i) + ', N=' + str(N), loc='left') fig.suptitle('EM Algorithm', fontsize=20) # gif画像を作成 params_anime = FuncAnimation(fig, update, frames=len(trace_mu_ikd), interval=100) params_anime.save('ch9_3_3_params.gif')

ランダムな状態から始まり、クラス(数字)に収束していくのを確認できます。
・学習の推移の確認
対数尤度の推移を作図します。
# 対数尤度の推移を作図 plt.figure(figsize=(8, 6)) plt.plot(np.arange(MaxIter), trace_L_i) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('EM Algorithm', fontsize=20) plt.title('Log Likelihood', loc='left') plt.grid() # グリッド線 plt.show()

更新を繰り返すごとに対数尤度が大きくなっているのを確認できます。各試行における上昇幅と先ほどのパラメータの変化の大きさが対応しています。
同様に、各パラメータの更新値の推移を作図します。初期値を持つパラメータは、x軸の値がMaxIter + 1個になります。
・コード(クリックで展開)
# 表示するクラス番号を指定 k = 0 # モデルのパラメータの推移を作図 plt.figure(figsize=(8, 6)) for d in range(D): plt.plot(np.arange(MaxIter + 1), np.array(trace_mu_ikd)[:, k, d], alpha=0.5, label='d=' + str(d)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('EM Algorithm', fontsize=20) plt.title('$\mu_{' + str(k) + '}$', loc='left') #plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
# 混合係数の推移を作図 plt.figure(figsize=(8, 6)) for k in range(K): plt.plot(np.arange(MaxIter + 1), np.array(trace_pi_ik)[:, k], alpha=1, label='k=' + str(k)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('EM Algorithm', fontsize=20) plt.title('$\pi$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()
# 表示するデータ番号を指定 n = 0 # 負担率の推移を作図 plt.figure(figsize=(8, 6)) for k in range(K): plt.plot(np.arange(MaxIter), np.array(trace_gamma_ink)[:, n, k], alpha=1, label='k=' + str(k)) plt.xlabel('iteration') plt.ylabel('value') plt.suptitle('EM Algorithm', fontsize=20) plt.title('$\gamma(z_{' + str(n) + '})$', loc='left') plt.legend() # 凡例 plt.grid() # グリッド線 plt.show()


入力データに含まれる数字(真のクラス)は一様に取り出しているので、推定(分類)したクラスの割合(=混合比率の推定値)も$\frac{1}{K}$に近付きます。

各データがどのクラスなのかの確率に相当します。分類されたクラスの値が1に近付いています。
・分類結果の確認
認識精度や交差エントロピー誤差を出したかったのですが、ランダムに分類されるためできませんでした。代わりにどうにかこうにか可視化してみました。こういう方法が良いのかは知りません。
真のクラスのデータごとにどのクラスに分類されているのかをカウントして割合を求めます。
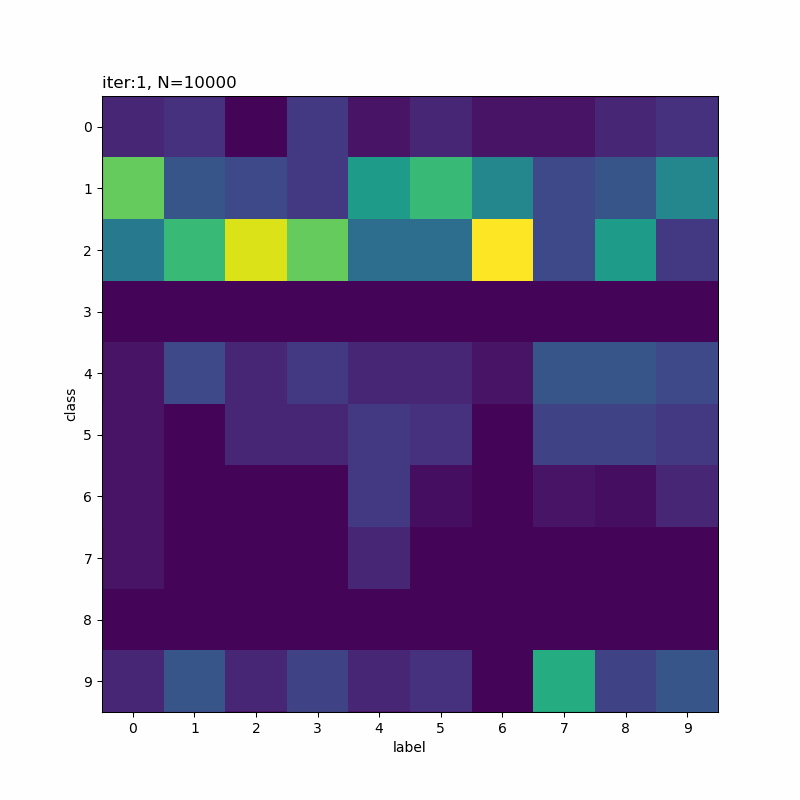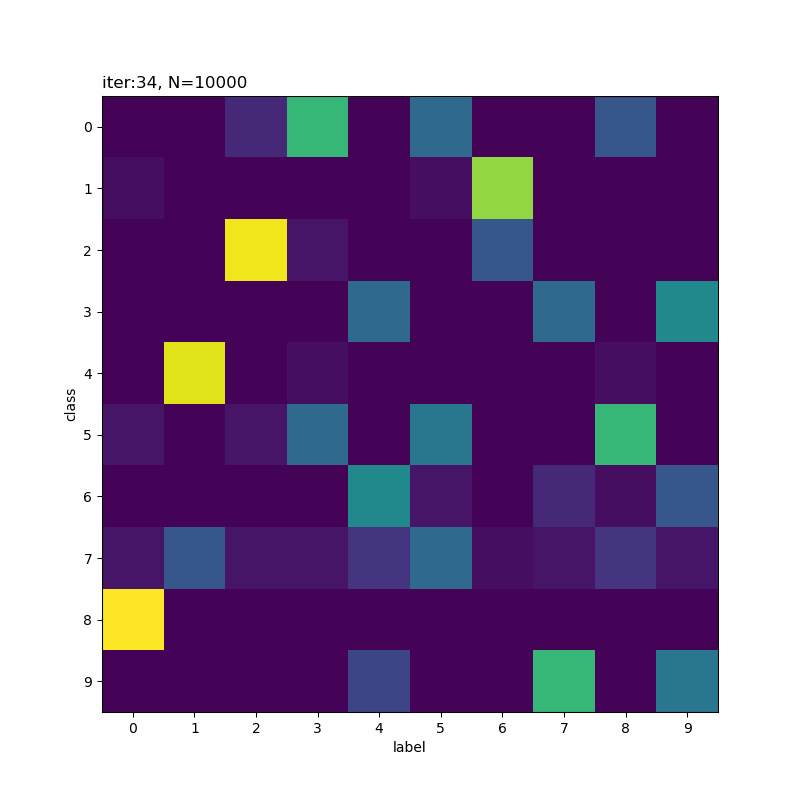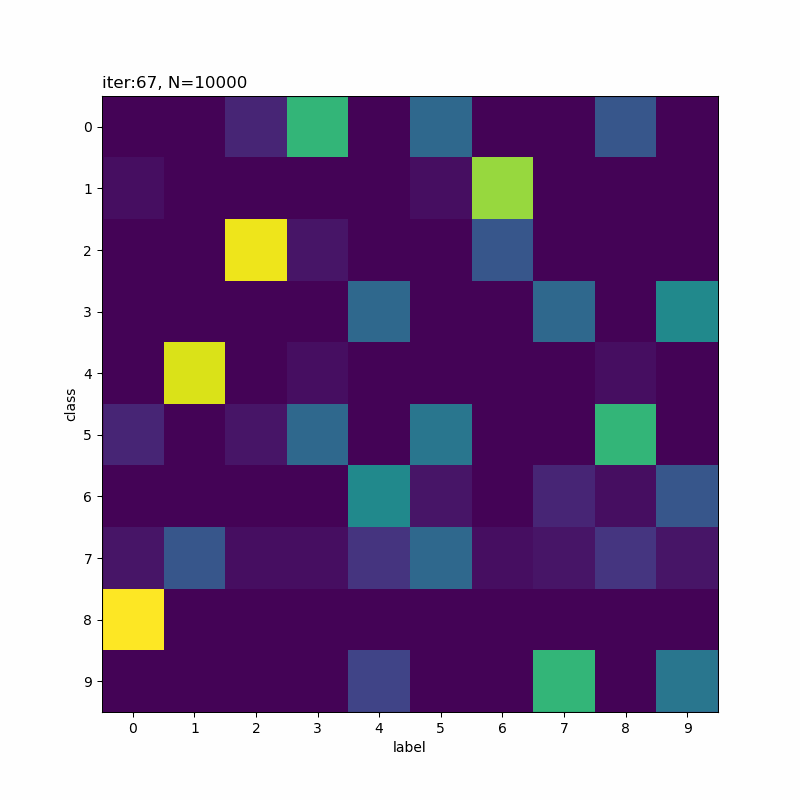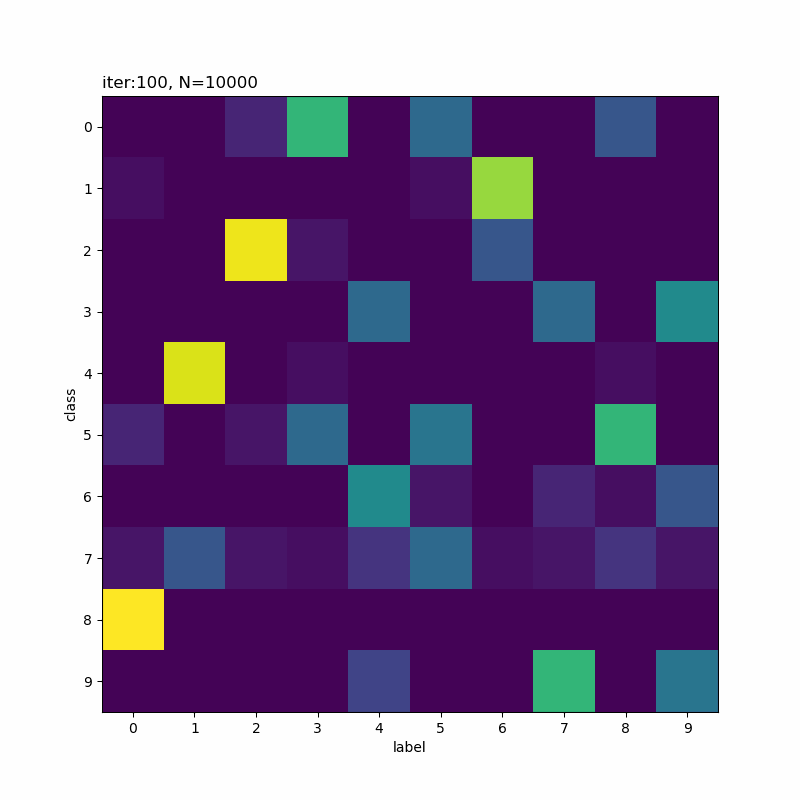
# 元の数字と分類先の関係をカウント res_rate_kk = np.zeros((K, K)) for lbl_k in range(K): # k番目の数字のデータにおいて、分類された(確率が最大の)クラス番号を抽出 res_cls_idx = np.argmax(gamma_nk[t_n == lbl_k], axis=1) #res_cls_idx = np.argmax(gamma_nk[t_n == label_list[lbl_k]], axis=1) # (数字を指定した場合) for cls_k in range(K): # k番目のクラスに分類された割合を計算 res_rate_kk[cls_k, lbl_k] = np.mean(res_cls_idx == cls_k)
利用する数字を指定した場合、ラベルの値がrange(K)と対応しません。そこで、label_list[lbl_k]とすることで対応させる必要があります。(その他のももっとうまく処理できるはず。)
ヒートマップにします。
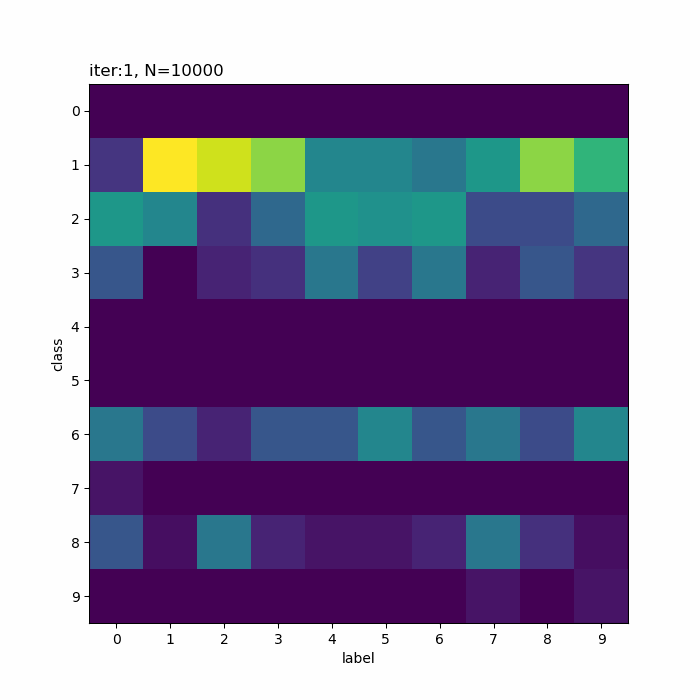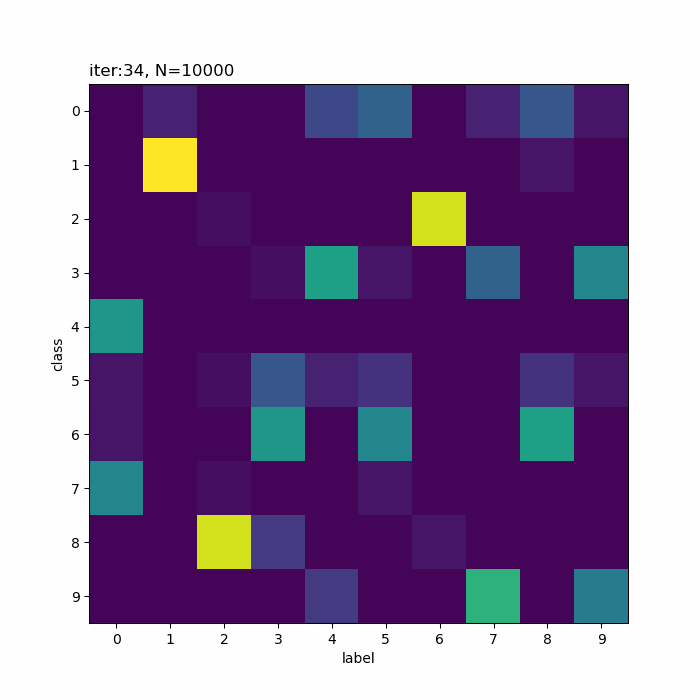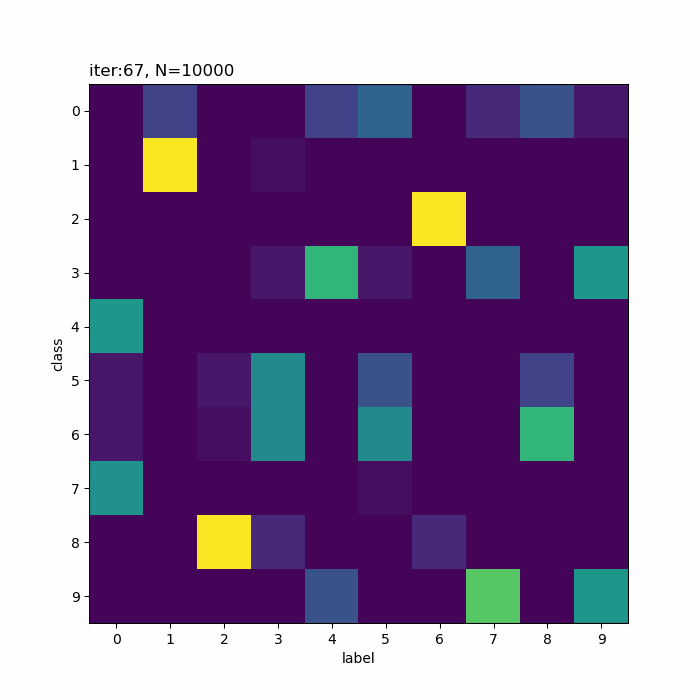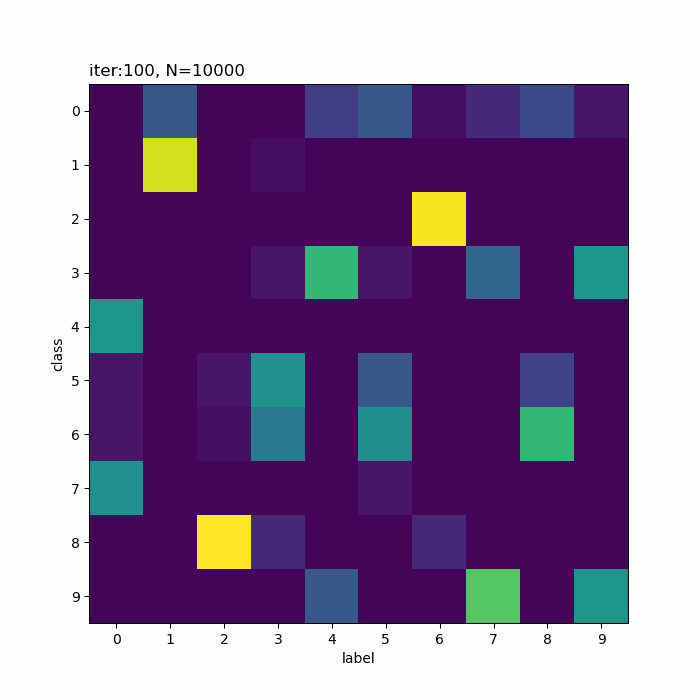
# 正解ラベルと分類クラスのヒートマップを作成 plt.figure(figsize=(8, 8)) plt.imshow(res_rate_kk) plt.xlabel('label') # x軸ラベル plt.ylabel('class') # y軸ラベル plt.xticks(np.arange(K)) # x軸目盛 #plt.xticks(np.arange(K), label_list) # x軸目盛:(数字を指定した場合) plt.yticks(np.arange(K)) # y軸目盛 plt.title('iter:' + str(i + 1) + ', N=' + str(N), loc='left') plt.colorbar() # 確率値 plt.show()

x軸が真のクラスでy軸が分類したクラスです。一対一で対応しているものや複数のクラスで迷っているようなものが分かります。
アニメーションでも確認してみましょう。
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(8, 8)) # 作図処理を関数として定義 def update(i): # i回目のカウント res_rate_kk = np.zeros((K, K)) for lbl_k in range(K): # k番目の数字のデータにおいて、分類された(確率が最大の)クラス番号を抽出 res_cls_idx = np.argmax(trace_gamma_ink[i][t_n == lbl_k], axis=1) #res_cls_idx = np.argmax(trace_gamma_ink[i][t_n == label_list[lbl_k]], axis=1) # (数字を指定した場合) for cls_k in range(K): # k番目のクラスに分類された割合を計算 res_rate_kk[cls_k, lbl_k] = np.mean(res_cls_idx == cls_k) # 前フレームのグラフを初期化 plt.cla() # i回目のヒートマップ plt.imshow(res_rate_kk) plt.xlabel('label') # x軸ラベル plt.ylabel('class') # y軸ラベル #plt.xticks(np.arange(K)) # x軸目盛 plt.xticks(np.arange(K), label_list) # x軸目盛:(数字を指定した場合) plt.yticks(np.arange(K)) # y軸目盛 plt.title('iter:' + str(i + 1) + ', N=' + str(N), loc='left') # gif画像を作成 cls_anime = FuncAnimation(fig, update, frames=len(trace_gamma_ink), interval=100) cls_anime.save('ch9_3_3_class.gif')
概ね1つのクラスに定まっていくのを確認できます。
・他の結果
データの設定を変えて結果を見てみます。

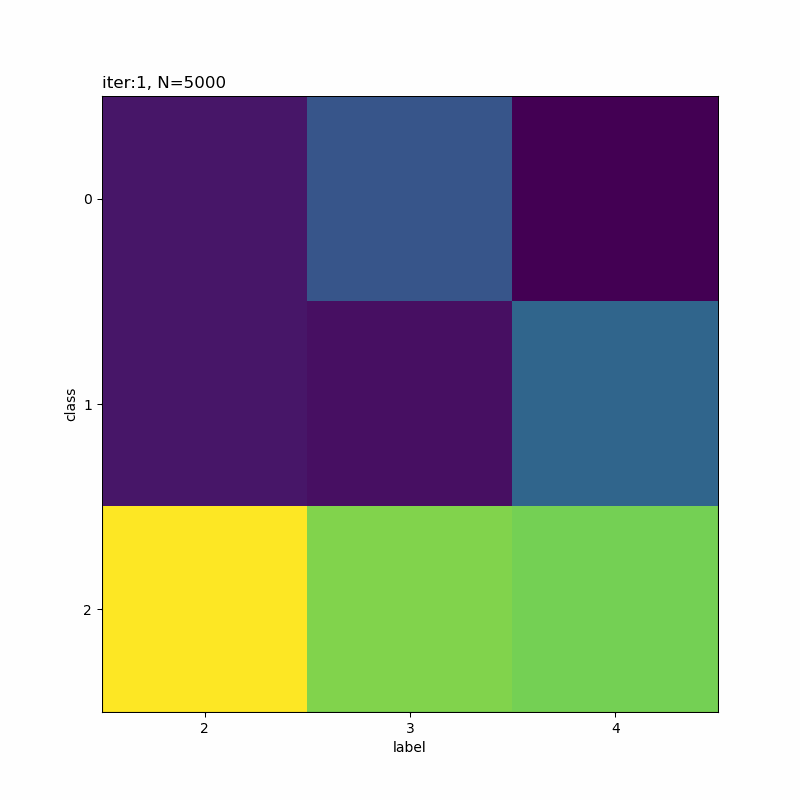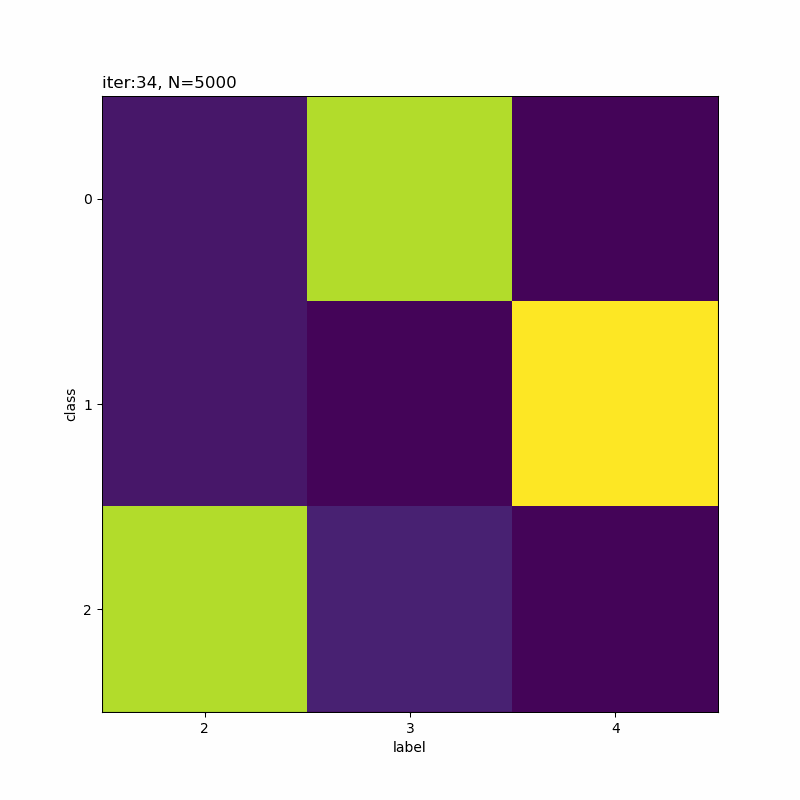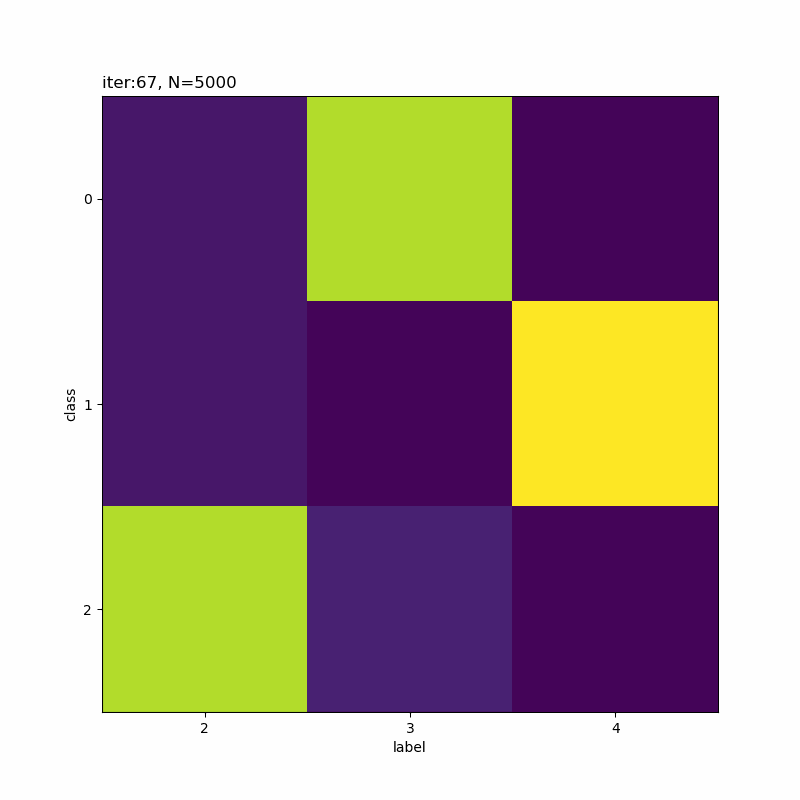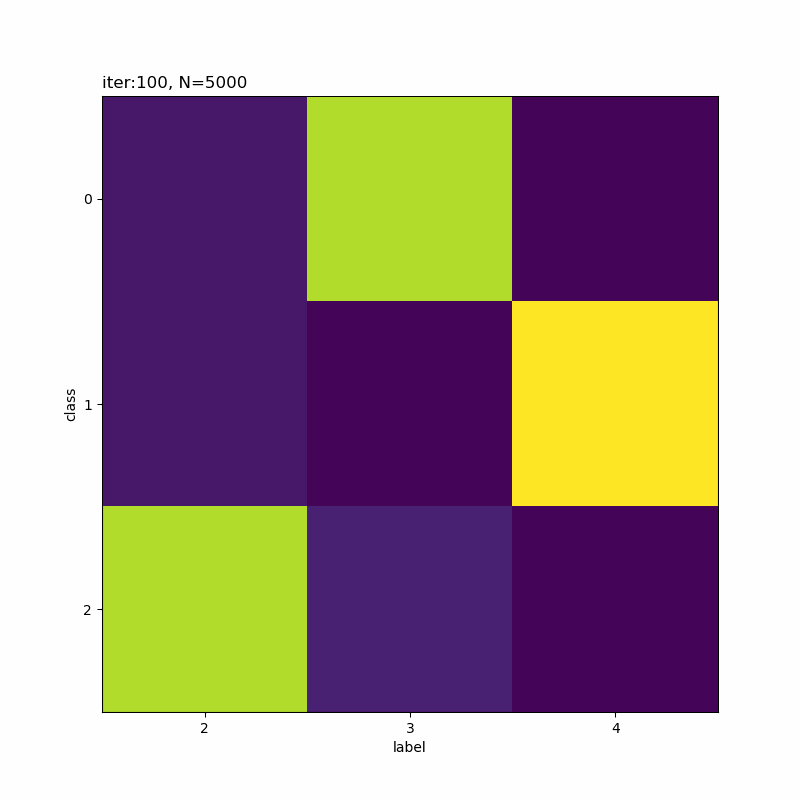
本の例だと余裕そうですね。だから選ばれたのかな。

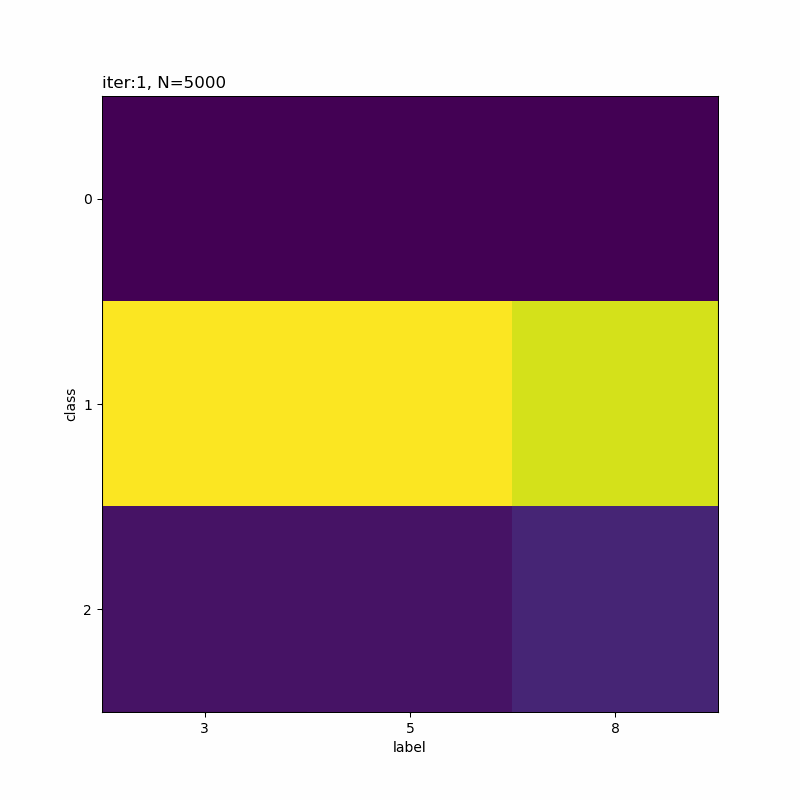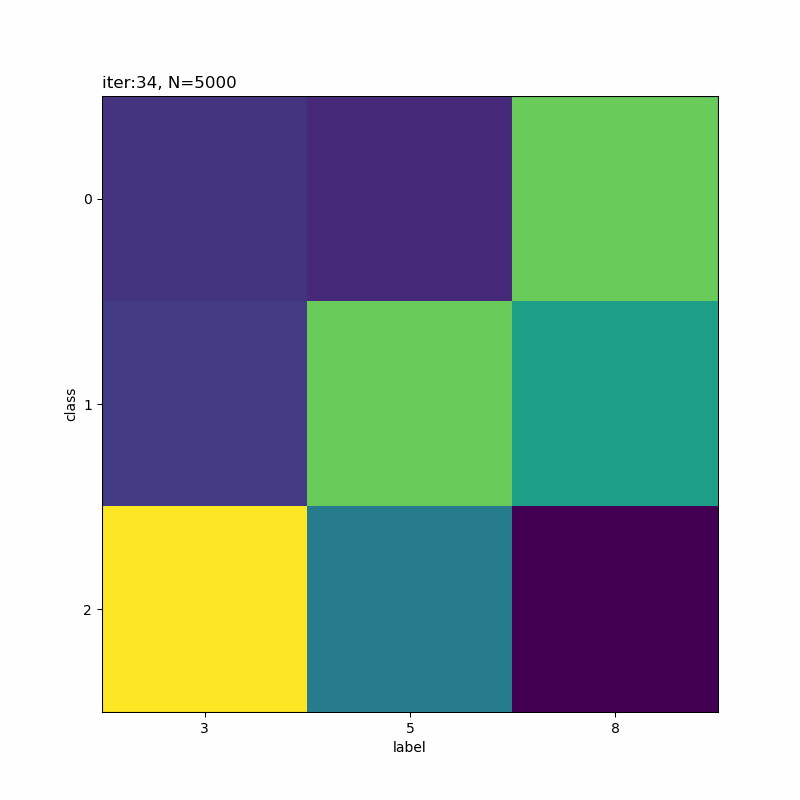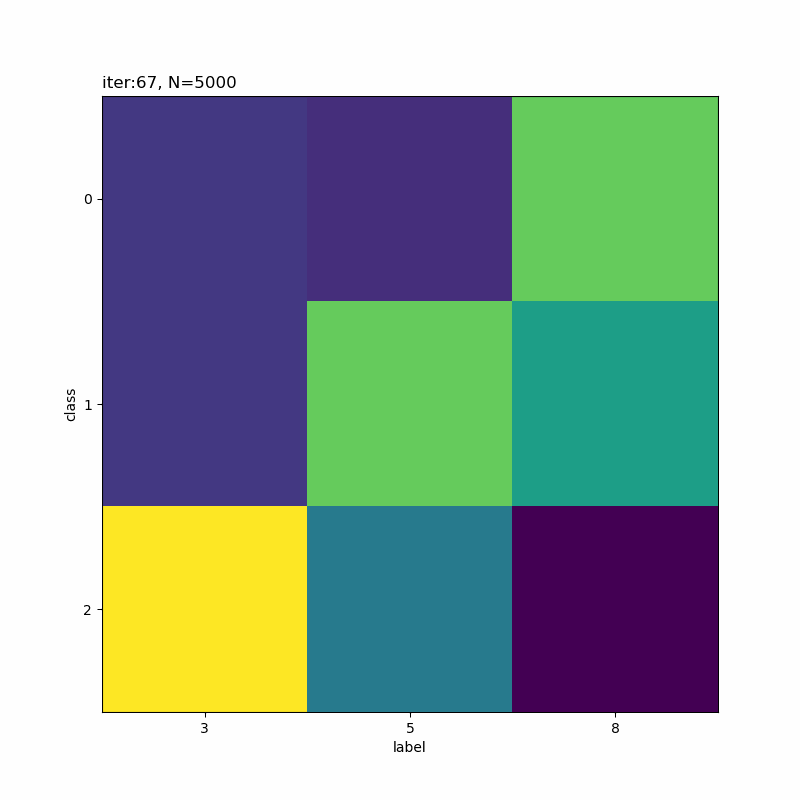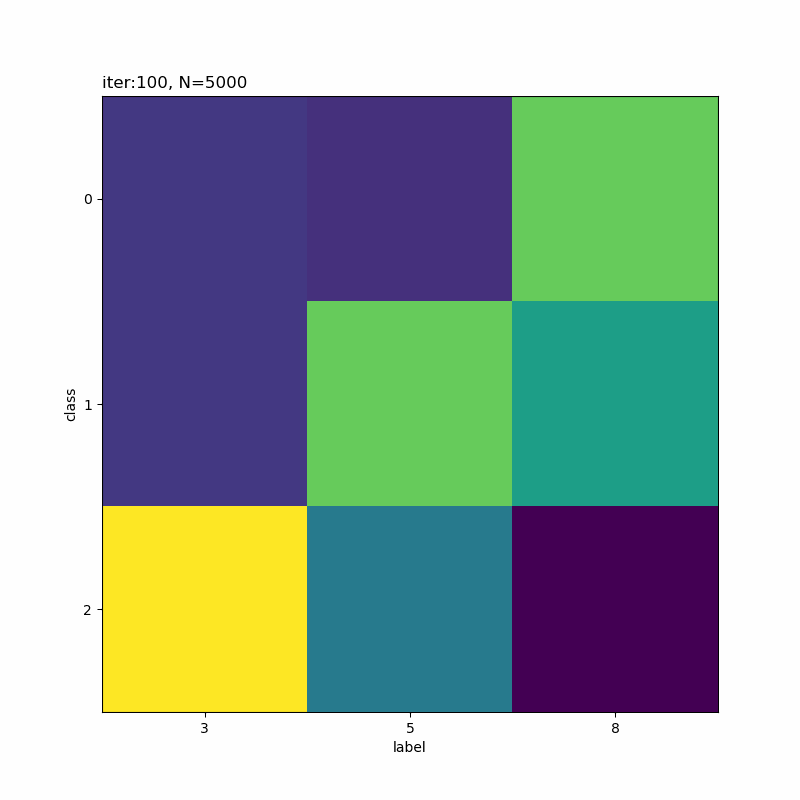
分類しにくそうなものを選んでみました。5と8が難しそうですね。他に、4・6・7も厳しい印象です。

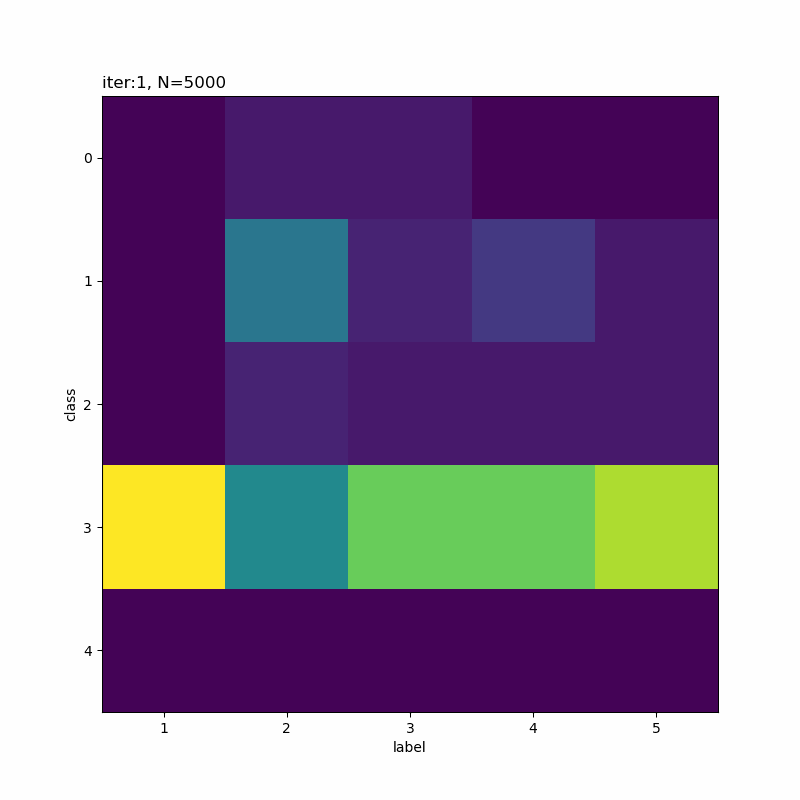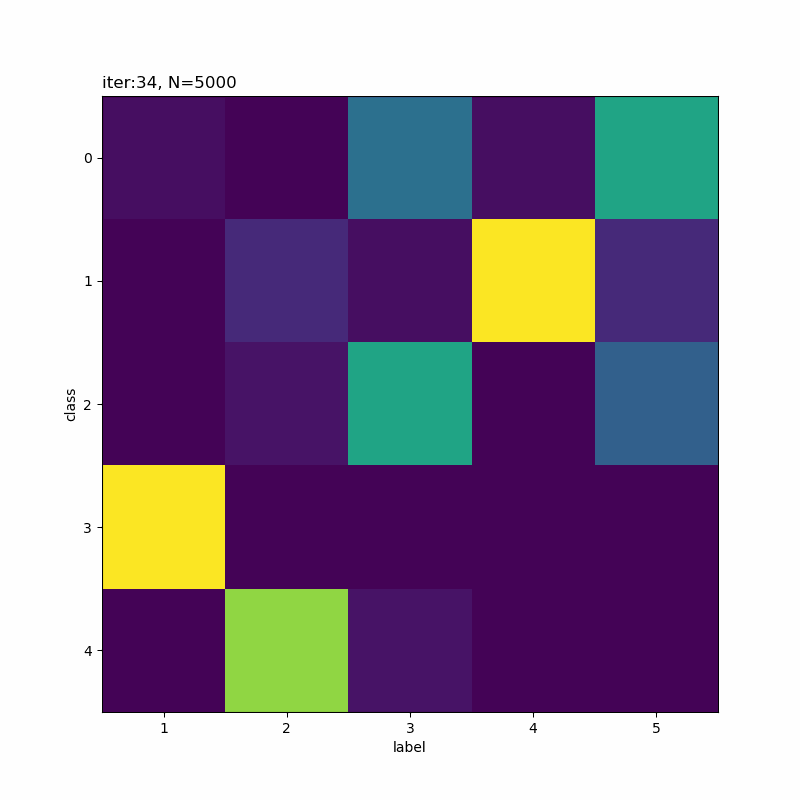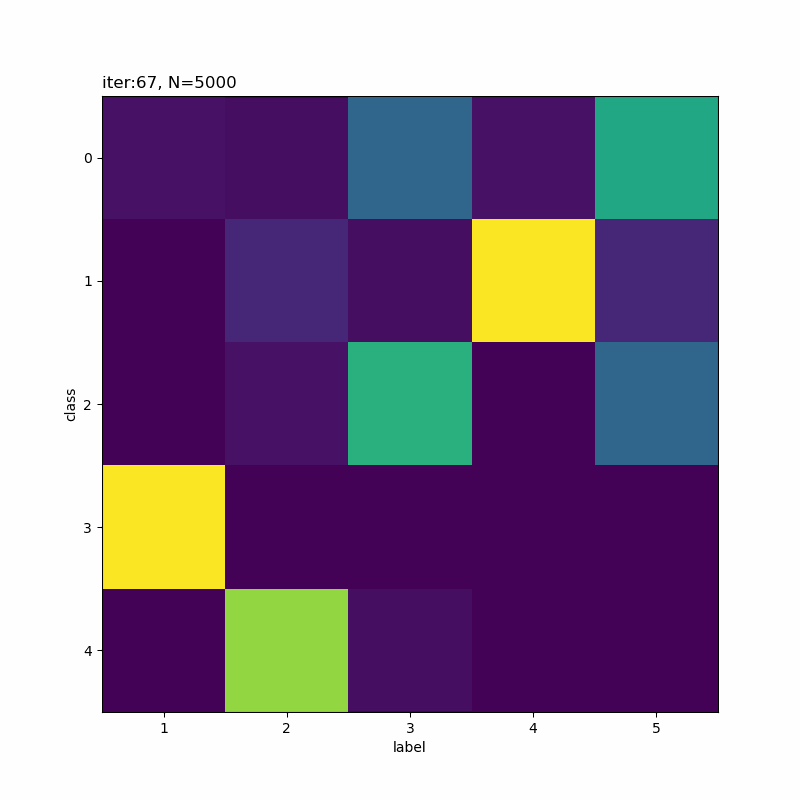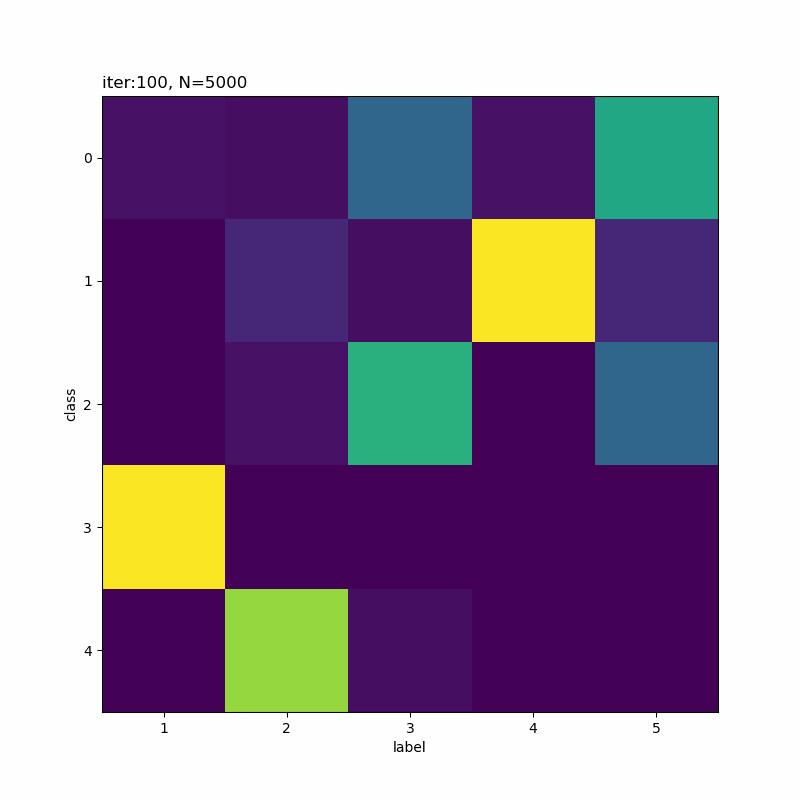
0番目のクラスが3から5に変化していますね。

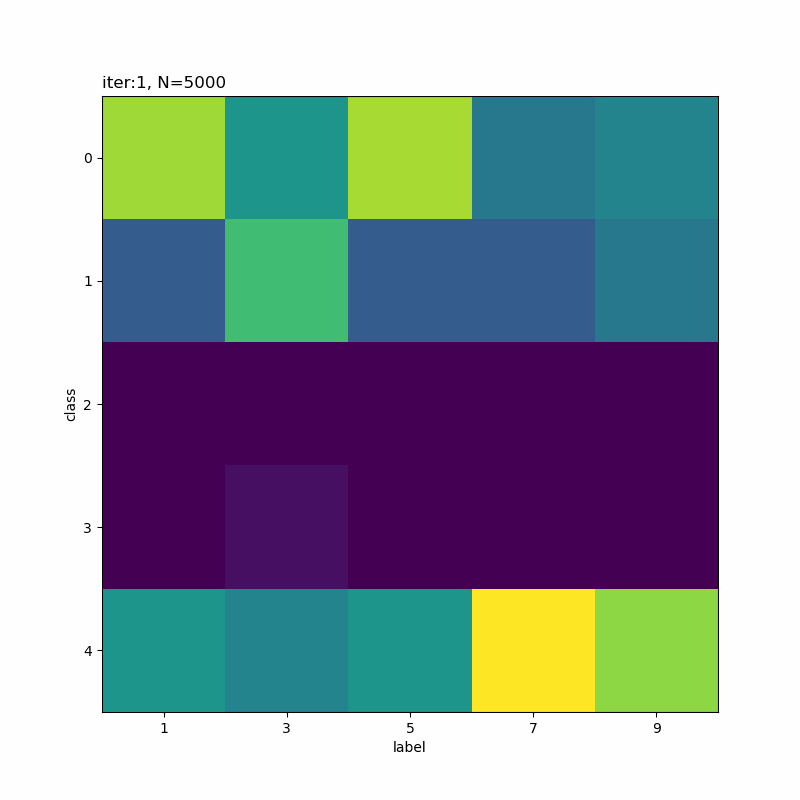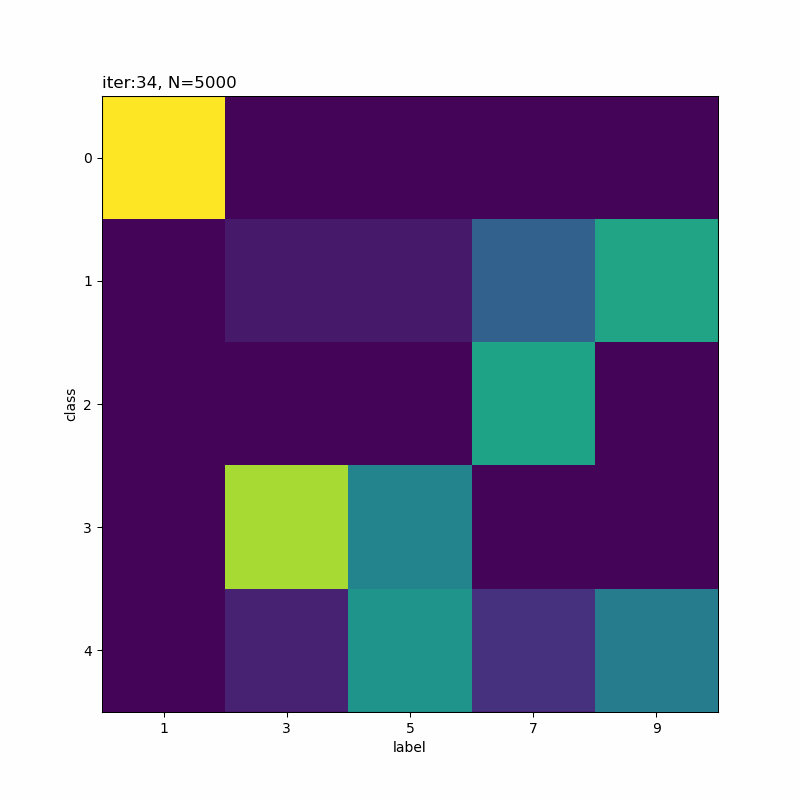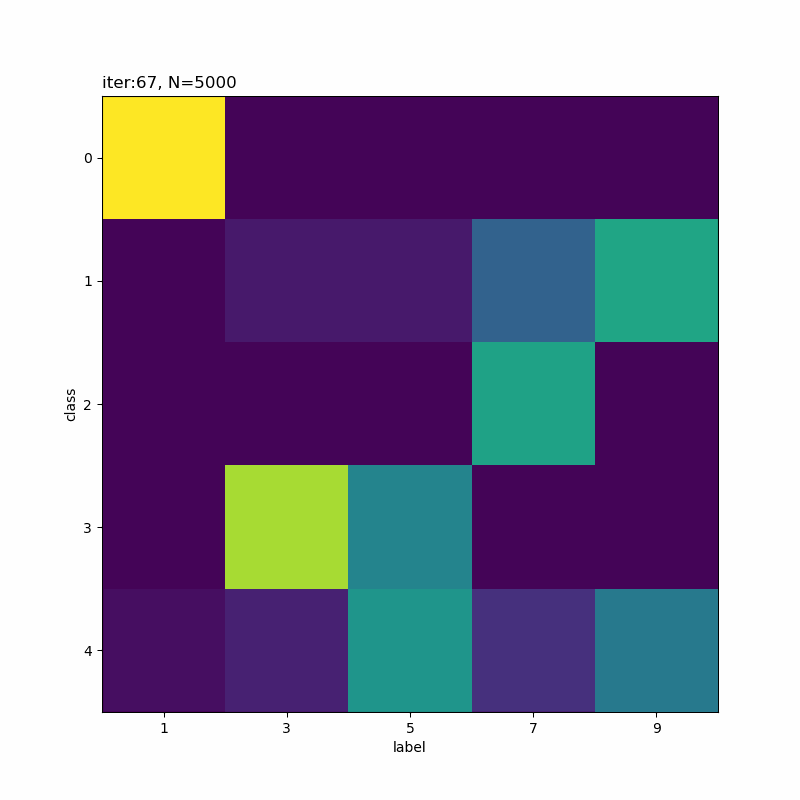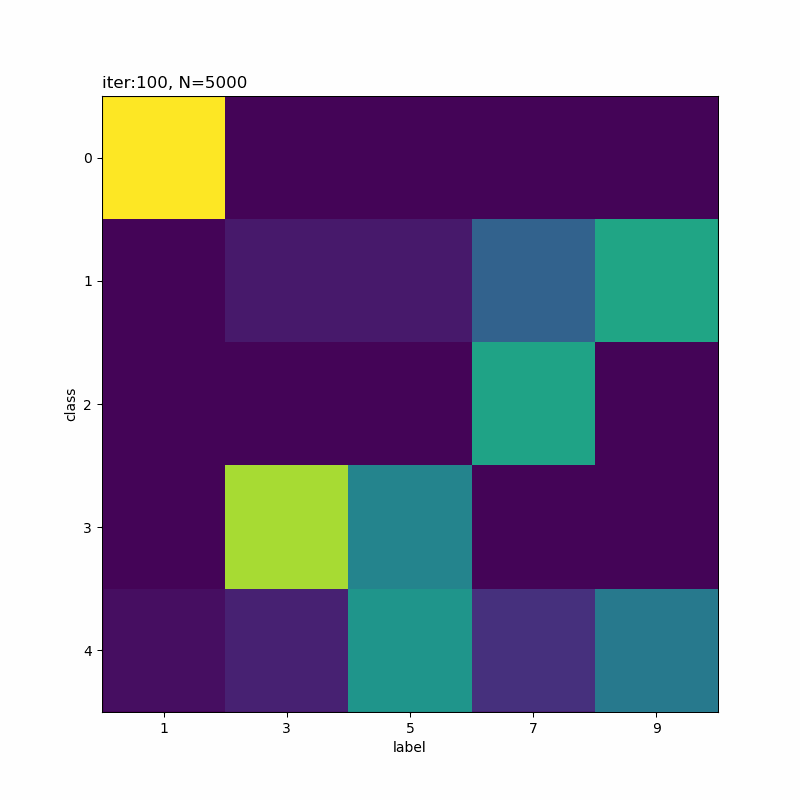
人の目には1,9,7,3,5になっているように見えなくもないですが、そこまで精度よく分類できていないように思えます。
(0から数えて)1つ目のクラスの色の濃い部分を見ると、「ク」の様な形状をしていて一部の「7」が引っかかってしまうのだろうと思います。同様に、クラス4も「う」のようでもあり左側を繋ぐと「5」も該当していまうのかな。同じ具合でクラス5が「5」と「9」になるのでしょう。
クラス1になった「9」とクラス4になった「9」を取り出して比べてみると面白いかもしれませんね。次の機会にはやってみます(メモ)。


思ったよりうまくできてるなぁ。まぁ何回か試した1回なわけですが。

クラス5が「0→4→3」のように変化しています。その隣のクラス6は「3・5・8」で迷っている感じです。また、クラス8は基本的に「2」なんですが、一瞬「3」が混ざります。
この「3」を追うと面白くて(?)、ラベル3のデータがクラス8に割り当てられたことで、クラス8のパラメータに「3」の特徴が含まれます。その後、クラス6、クラス5へと割り当てが変化することで、「3」の特徴も移っています。最終的に、クラス6ではラベル3のデータの影響が減ったことで、「5・8」の特徴が濃い結果になったのでしょう。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上下』,丸善出版,2012年.
おわりに
多次元ガウス分布のときは2次元のデータでやったので、データの分布を作図できてイメージしやすかったのですが、これはなんとも掴みにくかったです。784次元のデータが、2次元で言うxとyの点と同じだと思えば分かりました。
行間埋めをした段階では、分かった気でいたんですよね。私は数学もプログラムもほとんど独学なので、分かったつもりと理解したの境界が曖昧なようです。なので、数式を読むのと、プログラムを組むのと、言葉で説明するのアプローチを続けるのは大事だと改めて思いました。本当は図解するのも追加したい。どれかができても他ができなければ理解できていないと気付けるわけです。え?勉強会や輪読会に参加する?わ、私はネット上でも人見知るので、、、
そういや、生データと言うにはほど遠い綺麗に整ったデータですが、トイデータではないデータを使うのは久しぶり。
2021年7月2日は、Juice=Juiceの現リーダー金澤朋子さんの26歳のお誕生日です。
まずはソロ曲!
そしてグループ曲!!
元々好きだった曲をカバーしてくれて嬉しい♪
おめでとうございます!!!!!