はじめに
『ベイズ推論による機械学習入門』の学習時のノートです。基本的な内容は「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」になります。「数式」と「プログラム」から理解するのが目標です。
この記事は、3.4.3項の内容です。「尤度関数を平均と精度が未知の多次元ガウス分布(多変量正規分布)」、「事前分布をガウス・ウィシャート分布」とした場合の「パラメータの事後分布」と「未観測値の予測分布」の計算をPythonで実装します。
省略してある内容等ありますので、本とあわせて読んでください。初学者な自分が理解できるレベルまで落として書き下していますので、分かる人にはかなりくどくなっています。同じような立場の人のお役に立てれば幸いです。
【数式読解編】
【他の節の内容】
【この節の内容】
・Pythonでやってみよう
人工的に生成したデータを用いて、ベイズ推論を行ってみましょう。
利用するライブラリを読み込みます。
# 3.4.3項で利用するライブラリ import numpy as np from scipy.stats import multivariate_normal, multivariate_t # 多次元ガウス分布, 多次元スチューデントのt分布 import matplotlib.pyplot as plt
SciPyライブラリのstatsから多次元ガウス分布のクラスmultivariate_normalと多次元スチューデントのt分布のクラスmultivariate_tを利用します。それぞれのクラスの確率密度関数pdf()を使います。ただし、multivariate_tはバージョン1.6.0で追加された?もののようなのでSciPyをアップデートする必要があるかもしれません。
・観測モデルの構築
まずは、観測モデルを設定します。この例では、尤度$p(\mathbf{X} | \boldsymbol{\mu})$をデータごとに独立した多次元ガウス分布$\mathcal{N}(\mathbf{x}_n | \boldsymbol{\mu}, \boldsymbol{\Lambda}^{-1})$とします。
尤度のパラメータを設定します。この実装例では2次元のグラフで表現するため、$D = 2$のときのみ動作します。
# 真の平均パラメータを指定 mu_truth_d = np.array([25.0, 50.0]) # (既知の)分散共分散行列を指定 sigma2_truth_dd = np.array([[600.0, 100.0], [100.0, 400.0]]) # (既知の精度)行列を計算 lambda_truth_dd = np.linalg.inv(sigma2_truth_dd)
平均パラメータ$\boldsymbol{\mu} = (\mu_1, \cdots, \mu_D)$をmu_truth_dとして値を指定します。
分散共分散行列$\boldsymbol{\Sigma} = (\sigma_{1,1}^2, \cdots, \sigma_{D,D}^2)$をsigma2_truth_ddとして値を指定します。作図時に標準偏差に変換して利用します。$\sigma_{i,i}^2$は$i$次元方向の分散、$\sigma_{i,j}^2$は$i$次元と$j$次元方向の共分散です。
分散共分散行列の逆行列を精度行列と呼びます。sigma2_truth_ddから精度パラメータ(精度行列)$\boldsymbol{\Lambda} = \boldsymbol{\Sigma}^{-1}$を計算してlambda_truth_ddとします。逆行列はnp.linalg.inv()で計算できます。
この例ではmu_truth_dとlambda_truth_ddの両方が未知の値であり、この値を求めるのが目的です。
グラフ用の点を作成します。
# 作図用のxのx軸の値を作成 x_0_line = np.linspace( mu_truth_d[0] - 3 * np.sqrt(sigma2_truth_dd[0, 0]), mu_truth_d[0] + 3 * np.sqrt(sigma2_truth_dd[0, 0]), num=500 ) # 作図用のxのx軸の値を作成 x_1_line = np.linspace( mu_truth_d[1] - 3 * np.sqrt(sigma2_truth_dd[1, 1]), mu_truth_d[1] + 3 * np.sqrt(sigma2_truth_dd[1, 1]), num=500 ) # 格子状のxの値を作成 x_0_grid, x_1_grid = np.meshgrid(x_0_line, x_1_line) # xの点を作成 x_point_arr = np.stack([x_0_grid.flatten(), x_1_grid.flatten()], axis=1) x_dims = x_0_grid.shape print(x_dims)
(500, 500)
作図用に、2次元ガウス分布に従う変数$\mathbf{x}_n = (x_{n,1}, x_{n,2})$がとり得る点(2値の組み合わせ)を作成します。
$x_{n,1}$がとり得る値(x軸の値)をnp.linspace()で作成してx_0_lineとします。この例では、平均値を中心に標準偏差の3倍を範囲とします。np.linspace()を使うと指定した要素数で等間隔に切り分けます。np.arange()を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。$i$軸の標準偏差$\sigma_{i,i}$は、分散の平方根$\sigma_{i,i} = \sqrt{\sigma_{i,i}^2}$です。平方根はnp.sqrt()で計算できます。同様に、$x_{n,2}$がとり得る値(y軸の値)も作成してx_1_lineとします。
x_0_lineとx_1_lineの要素の全ての組み合わせを持つ配列をnp.meshgrid()で作成してx_0_girdとx_1_gridとします。これは、確率密度を等高線図にする際に格子状の点(2軸の全ての値が直交する点)を渡す必要があるためです。
また、x_0_girdとx_1_gridを1列に並べたものをnp.stack()で列方向に結合してx_point_arrとします。こちらは確率密度の計算に使います。
作成した$\mathbf{x}$の点は次のようになります。
# 尤度を計算:式(2.72)
true_model = multivariate_normal.pdf(
x=x_point_arr, mean=mu_truth_d, cov=np.linalg.inv(lambda_truth_dd)
)
x_point_arrの値(の組み合わせ)ごとに確率密度を計算します。多次元ガウス分布の確率密度は、multivariate_normal.pdf()で計算できます。データの引数Xにx_point_arr、平均の引数muにmu_d、分散共分散行列の引数sigmaにlambda_truth_ddを逆行列$\boldsymbol{\Sigma} = \boldsymbol{\Lambda}^{-1}$に変換して指定します。勿論sigma2_truth_ddを指定すればいいのですが、ここでは式に合わせてlambda_truth_ddを使っています。
計算結果を確認しましょう。
# 確認 print(x_point_arr) print(true_model)
[[-48.48469228 -10. ]
[-48.19016446 -10. ]
[-47.89563663 -10. ]
...
[ 97.89563663 110. ]
[ 98.19016446 110. ]
[ 98.48469228 110. ]]
[1.88323099e-07 1.94035442e-07 1.99890897e-07 ... 1.99890897e-07
1.94035442e-07 1.88323099e-07]
true_modelは、x_dimsを使ってx_1_grid, x_2_gridと同じ形状に変換してから作図に使います。
尤度を作図します。
# 尤度を作図 plt.figure(figsize=(12, 9)) plt.contour(x_0_grid, x_1_grid, true_model.reshape(x_dims)) # 尤度 plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$\mu=[' + ', '.join([str(mu) for mu in mu_truth_d]) + ']' + ', \Lambda=' + str([list(lmd_d) for lmd_d in np.round(lambda_truth_dd, 5)]) + '$', loc='left') plt.colorbar() plt.show()
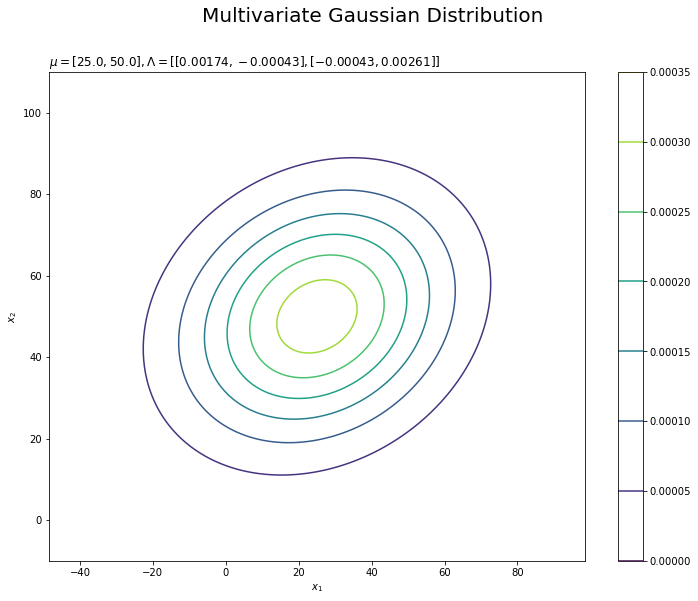
plt.contour()で等高線グラフを描画します。格子状の点を渡す必要があります。
真のパラメータを求めることは、この真の分布を求めることを意味します。
・データの生成
続いて、構築したモデルに従って観測データ$\mathbf{X} = \{\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N\}$を生成します。
多次元ガウス分布に従う$N$個のデータをランダムに生成します。
# (観測)データ数を指定 N = 50 # 多次元ガウス分布に従うデータを生成 x_nd = np.random.multivariate_normal( mean=mu_truth_d, cov=np.linalg.inv(lambda_truth_dd), size=N )
生成するデータ数$N$をNとして値を指定します。
多次元ガウス分布に従う乱数は、np.random.multivariate_normal()で生成できます。試行回数の引数sizeにNを指定します。他の引数についてはmultivariate_normal.pdf()と同じです。生成したN個のデータをx_ndとします。
観測したデータを確認しましょう。
# 確認 print(x_nd[:5])
[[ 0.60303781 88.19483249]
[ 46.11086879 49.04271005]
[ 22.65545125 67.44997697]
[ -7.79197304 37.27265151]
[-13.52466523 26.30906421]]
観測データの散布図を尤度と重ねて確認します。
# 観測データの散布図を作成 plt.figure(figsize=(12, 9)) plt.scatter(x=x_nd[:, 0], y=x_nd[:, 1]) # 観測データ plt.contour(x_0_grid, x_1_grid, true_model.reshape(x_dims)) # 真の分布 plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$N=' + str(N) + ', \mu=[' + ', '.join([str(mu) for mu in mu_truth_d]) + ']' + ', \Lambda=' + str([list(lmd_d) for lmd_d in np.round(lambda_truth_dd, 5)]) + '$', loc='left') plt.colorbar() plt.show()
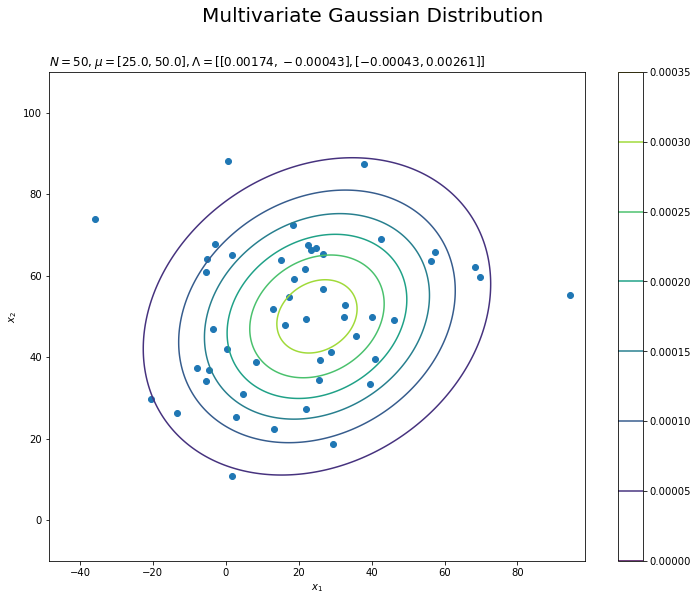
plt.scatter()で散布図を描画します。
・事前分布の設定
次に、尤度に対する共役事前分布を設定します。多次元ガウス分布の平均パラメータ$\boldsymbol{\mu}$と精度パラメータ$\boldsymbol{\Lambda}$に対する事前分布$p(\boldsymbol{\mu}, \boldsymbol{\Lambda})$として、ガウス・ウィシャート分布$\mathrm{NW}(\boldsymbol{\mu}, \boldsymbol{\Lambda} | \mathbf{m}, \beta, \nu, \mathbf{W})$を設定します。
$\boldsymbol{\mu}$の事前分布のパラメータ(超パラメータ)を設定します。
# muの事前分布のパラメータを指定 m_d = np.array([0.0, 0.0]) beta = 1.0 # lambdaの事前分布のパラメータを指定 nu = 2.0 w_dd = np.array([[0.0005, 0], [0, 0.0005]])
多次元ガウス分布の平均パラメータ$\mathbf{m} = (m_1, \cdots, m_D)$をm_d、精度パラメータの係数$\beta$をbetaとして値を指定します。
ウィシャート分布の自由度$\nu$をnu、パラメータ$\mathbf{W} = (w_{1,1}, \cdots, w_{D,D})$をw_ddとして値を指定します。$\nu$は$D - 1$より大きい値、$\mathbf{W}$は正定値行列である必要があります。
事前分布のパラメータを設定できたので、これまでのように事前分布をグラフで確認しましょう。しかし、この例では精度パラメータ$\boldsymbol{\Lambda}$が未知の値なので、$\boldsymbol{\mu}$の事前分布$\mathcal{N}(\boldsymbol{\mu} | \mathbf{m}, (\beta \boldsymbol{\Lambda})^{-1})$の精度パラメータ$\beta \boldsymbol{\Lambda}$が分かりません。そこで、$\boldsymbol{\Lambda}$の事前分布$\mathcal{W}(\boldsymbol{\Lambda} | \nu, \mathbf{W})$から精度パラメータの期待値$\mathbb{E}[\boldsymbol{\Lambda}]$を求めて、$\boldsymbol{\Lambda}$の代わりに利用することにします。
# lambdaの期待値を計算:式(2.89)
E_lambda_dd = nu * w_dd
精度パラメータの期待値は、ウィシャート分布の期待値(2.89)より
で計算できます。
$\boldsymbol{\mu}$の事前分布の確率密度を計算します。
# muの事前分布の分散共分散行列を計算 E_sigma2_mu_dd = np.linalg.inv(beta * E_lambda_dd) # 作図用のmuのx軸の値を作成 mu_0_line = np.linspace( mu_truth_d[0] - 2 * np.sqrt(E_sigma2_mu_dd[0, 0]), mu_truth_d[0] + 2 * np.sqrt(E_sigma2_mu_dd[0, 0]), num=500 ) # 作図用のmuのy軸の値を作成 mu_1_line = np.linspace( mu_truth_d[1] - 2 * np.sqrt(E_sigma2_mu_dd[1, 1]), mu_truth_d[1] + 2 * np.sqrt(E_sigma2_mu_dd[1, 1]), num=500 ) # 格子状の点を作成 mu_0_grid, mu_1_grid = np.meshgrid(mu_0_line, mu_1_line) # muの点を作成 mu_point_arr = np.stack([mu_0_grid.flatten(), mu_1_grid.flatten()], axis=1) mu_dims = mu_0_grid.shape
$\mathbf{x}$の点のときと同様に、2次元ガウス分布に従う変数$\boldsymbol{\mu} = (\mu_1, \mu_2)$がとり得る値を作成してmu_point_matとします。この例では、真の値を中心に$\boldsymbol{\mu}$の事前分布の標準偏差の2倍を範囲とします。$(\beta \mathbb{E}[\boldsymbol{\Lambda}])^{-1}$を$\boldsymbol{\mu}$の事前分布の分散共分散行列E_sigma2_mu_ddとして標準偏差を計算しています。
$\boldsymbol{\mu}$の事前分布の確率密度を計算します。
# muの事前分布を計算:式(2.72)
prior_mu = multivariate_normal.pdf(
x=mu_point_arr, mean=m_d, cov=np.linalg.inv(E_lambda_dd)
)
m_dとbeta, E_lambda_ddを用いて、尤度のときと同様にしてmu_point_arrの値ごとに確率密度を計算します。
計算結果は次のようになります。
# 確認 print(mu_point_arr) print(prior_mu)
[[-38.2455532 -13.2455532 ]
[-37.99206401 -13.2455532 ]
[-37.73857482 -13.2455532 ]
...
[ 87.73857482 113.2455532 ]
[ 87.99206401 113.2455532 ]
[ 88.2455532 113.2455532 ]]
[7.01611475e-05 7.08423800e-05 7.15256308e-05 ... 5.56405454e-09
5.44149678e-09 5.32129663e-09]
$\boldsymbol{\mu}$の事前分布を作図します。
# muの事前分布を作図 plt.figure(figsize=(12, 9)) plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真の値 plt.contour(mu_0_grid, mu_1_grid, prior_mu.reshape(mu_dims)) # muの事前分布 plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$\\beta=' + str(beta) + ', m=[' + ', '.join([str(m) for m in m_d]) + ']' + ', E[\Lambda]=' + str([list(lmd_d) for lmd_d in np.round(E_lambda_dd, 5)]) + '$', loc='left') plt.colorbar() plt.show()

$\boldsymbol{\mu}$の真の値を確率密度のグラフと重ねて表示します。
$\boldsymbol{\Lambda}$についても事前分布(の確率密度)を計算してグラフで確認したいところですが、精度行列の分布はイメージしにくいため、平均パラメータの期待値$\mathbb{E}[\boldsymbol{\mu}]$と精度パラメータの期待値$\mathbb{E}[\boldsymbol{\Lambda}]$を用いた多次元ガウス分布を尤度と比較することにしましょう。ちなみに、ウィシャート分布の確率密度はwishart.pdf()で計算できます(たぶん)。
# muの期待値を計算:式(2.76)
E_mu_d = m_d
平均パラメータの期待値は、ガウス分布の期待値(3.76)、より
です。
$\boldsymbol{\mu}$の事前分布の期待値(平均パラメータの期待値)と$\boldsymbol{\Lambda}$の事前分布の期待値(精度パラメータの期待値)を用いて、多次元ガウス分布の多次元ガウス分布の確率密度を計算します。
# 事前分布の期待値を用いた分布を計算:式(2.72)
prior_lambda = multivariate_normal.pdf(
x=x_point_arr, mean=E_mu_d, cov=np.linalg.inv(beta * E_lambda_dd)
)
E_mu_d, E_lambda_ddを用いて、尤度のときと同様にして計算します。
計算結果は次のようになります。
# 確認 print(prior_lambda)
[4.67351015e-05 4.74052147e-05 4.80807653e-05 ... 3.11383678e-09
3.02520632e-09 2.93884364e-09]
$\boldsymbol{\mu}$と$\boldsymbol{\Lambda}$の事前分布の期待値(平均と精度パラメータの期待値)を用いた分布を作図します。
# 事前分布の期待値を用いた分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_0_grid, x_1_grid, true_model.reshape(x_dims), alpha=0.5, linestyles='--') # 真の分布 plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真のmu plt.contour(x_0_grid, x_1_grid, prior_lambda.reshape(x_dims)) # 事前分布の期待値を用いた分布 plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$m=[' + ', '.join([str(m) for m in m_d]) + ']' + ', \\nu=' + str(nu) + ', W=' + str([list(w_d) for w_d in np.round(w_dd, 5)]) + '$', loc='left') plt.colorbar() plt.show()
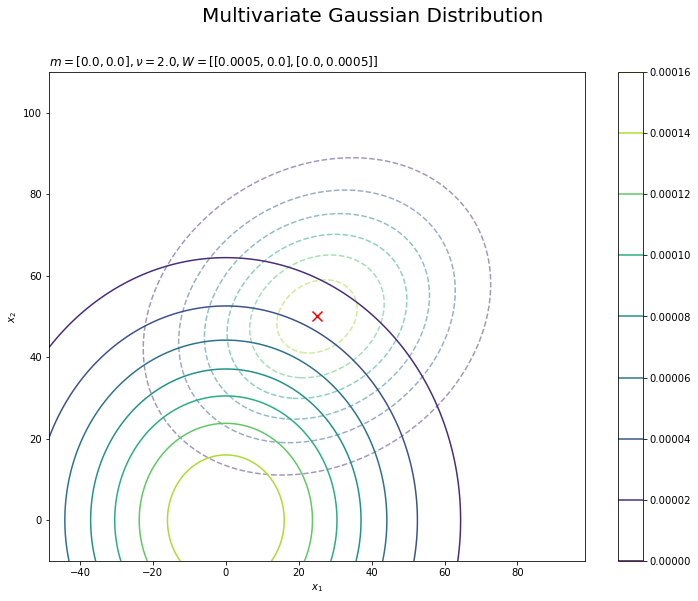
尤度を破線で重ねて描画します。
・事後分布の計算
観測データ$\mathbf{X}$からパラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda}$の事後分布$p(\boldsymbol{\mu}, \boldsymbol{\Lambda} | \mathbf{X})$を求めます(パラメータ$\boldsymbol{\mu},\ \boldsymbol{\Lambda}$を分布推定します)。事後分布はガウス・ウィシャート分布$\mathrm{NW}(\boldsymbol{\mu} | \hat{\mathbf{m}}, \hat{\boldsymbol{\Lambda}}_{\boldsymbol{\mu}}^{-1}, \hat{\nu}, \hat{\mathbf{W}})$になります。
観測データx_ndを用いて、$\boldsymbol{\mu}$の事後分布のパラメータを計算します。
# muの事後分布のパラメータを計算:式(3.129) beta_hat = N + beta m_hat_d = (np.sum(x_nd, axis=0) + beta * m_d) / beta_hat
事後分布のパラメータを
で計算して、結果をbeta_hat、m_hat_dとします。
# 確認 print(beta_hat) print(m_hat_d)
51.0
[20.00090437 49.56291415]
$\boldsymbol{\Lambda}$の事後分布のパラメータも計算します。
# lambdaの事後分布のパラメータを計算:式(3.133) term_x_dd = np.dot(x_nd.T, x_nd) term_m_dd = beta * np.dot(m_d.reshape([2, 1]), m_d.reshape([1, 2])) term_m_hat_dd = beta_hat * np.dot(m_hat_d.reshape([2, 1]), m_hat_d.reshape([1, 2])) w_hat_dd = np.linalg.inv( term_x_dd + term_m_dd - term_m_hat_dd + np.linalg.inv(w_dd) ) nu_hat = N + nu
事後分布のパラメータを
で計算して、結果をw_hat_dd、nu_hatとします。ただし、$\sum_{n=1}^N \mathbf{x}_n \mathbf{x}_n^{\top}$の計算を効率よく処理するために、$\mathbf{X}^{\top} \mathbf{X}$で計算しています。
# 確認 print(w_hat_dd) print(nu_hat)
[[ 3.28887083e-05 -8.45877039e-06]
[-8.45877039e-06 5.40984235e-05]]
52.0
事前分布のときと同様に、求めたパラメータを用いて、学習後の精度パラメータの期待値$\mathbb{E}[\hat{\boldsymbol{\Lambda}}]$を計算します。
# lambdaの期待値を計算:式(2.89) E_lambda_hat_dd = nu_hat * w_hat_dd # 確認 print(E_lambda_hat_dd)
[[ 0.00171021 -0.00043986]
[-0.00043986 0.00281312]]
$\boldsymbol{\mu}$の事後分布の確率密度を計算します。
# muの事後分布を計算:式(2.72)
posterior_mu = multivariate_normal.pdf(
x=mu_point_arr, mean=m_hat_d, cov=np.linalg.inv(beta_hat * E_lambda_hat_dd)
)
更新した超パラメータm_hat_d, lambda_lambda_hat_ddを用いて、事前分布のときと同様にして計算します。
計算結果は次のようになります。
# 確認 print(posterior_mu)
[5.34190595e-154 1.35099504e-153 3.39763919e-153 ... 1.04803411e-173
3.35743488e-174 1.06956150e-174]
$\boldsymbol{\mu}$の事後分布を作図します。
# muの事後分布を作図 plt.figure(figsize=(12, 9)) plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真の値 plt.contour(mu_0_grid, mu_1_grid, posterior_mu.reshape(mu_dims)) # muの事後分布 plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$N=' + str(N) + ', \hat{m}=[' + ', '.join([str(m) for m in np.round(m_hat_d, 1)]) + ']' + ', \hat{\\beta}=' + str(beta_hat) + ', E[\hat{\Lambda}]=' + str([list(lmd_d) for lmd_d in np.round(E_lambda_hat_dd, 5)]) + '$', loc='left') plt.colorbar() plt.show()
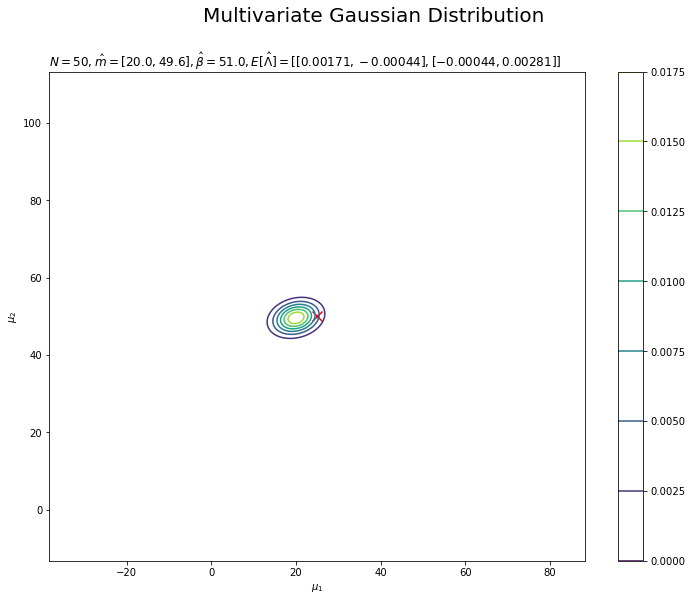
$\boldsymbol{\mu}$の真の値付近をピークとする分布を推定できています。分布が小さくなったわけではなく、かなり先の尖った形をしています。
$\boldsymbol{\Lambda}$の事後分布についても事前分布のときと同様に、パラメータの期待値を用いた分布を確認しましょう。学習後の平均パラメータの期待値$\mathbb{E}[\hat{\boldsymbol{\mu}}]$を計算します。
# muの期待値を計算:式(2.76) E_mu_hat_d = m_hat_d # 確認 print(E_mu_hat_d)
[20.00090437 49.56291415]
$\boldsymbol{\mu}$と$\boldsymbol{\Lambda}$の事後分布の期待値(平均と精度パラメータの期待値)を用いて、多次元ガウス分布の確率密度を計算します。
# 事後分布の期待値を用いた分布を計算:式(2.72)
posterior_lambda = multivariate_normal.pdf(
x=x_point_arr, mean=E_mu_hat_d, cov=np.linalg.inv(E_lambda_hat_dd)
)
E_mu_hat_d, E_lambda_hat_ddを用いて、尤度のときと同様にして計算します。
計算結果は次のようになります。
# 確認 print(posterior_lambda)
[2.53670294e-07 2.60536086e-07 2.67548012e-07 ... 8.88722625e-08
8.61180937e-08 8.34368979e-08]
$\boldsymbol{\mu}$と$\boldsymbol{\Lambda}$の事後分布の期待値(平均と精度パラメータの期待値)を用いた分布を作図します。
# 事後分布の期待値を用いた分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_0_grid, x_1_grid, true_model.reshape(x_dims), alpha=0.5, linestyles='--') # 真の分布 plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真のmu plt.contour(x_0_grid, x_1_grid, posterior_lambda.reshape(x_dims)) # 事後分布の期待を用いた分布 plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$N=' + str(N) + ', \hat{m}=[' + ', '.join([str(m) for m in np.round(m_hat_d, 1)]) + ']' + ', \hat{\\nu}=' + str(nu_hat) + ', \hat{W}=' + str([list(w_d) for w_d in np.round(w_hat_dd, 5)]) + '$', loc='left') plt.colorbar() plt.show()
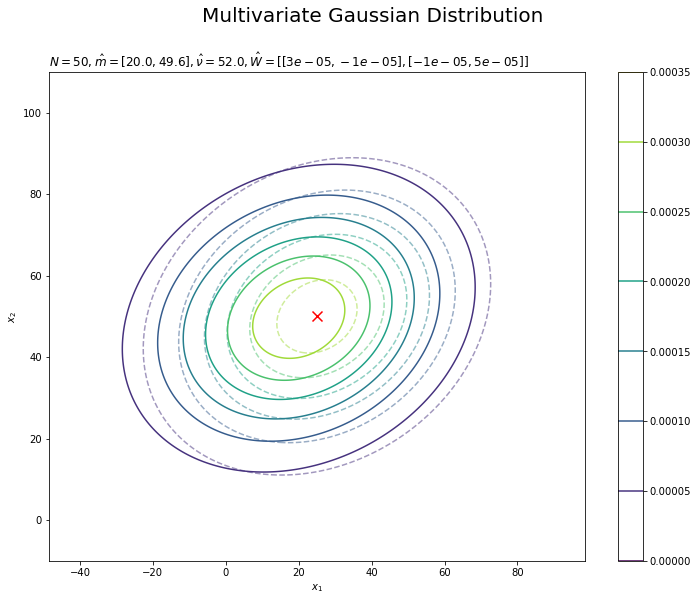
分布の形状が近づいているのを確認できます。
・予測分布の計算
最後に、観測データ$\mathbf{X}$から未観測のデータ$\mathbf{x}_{*}$の予測分布$p(\mathbf{x}_{*} | \mathbf{X})$を求めます。予測分布はスチューデントのt分布$p(\mathbf{x}_{*} | \hat{\boldsymbol{\mu}}_s, \hat{\boldsymbol{\Lambda}}_s, \hat{\nu}_s)$になります。
事後分布のパラメータを用いて、予測分布のパラメータを計算します。
# 次元数を取得 D = len(m_d) # 予測分布のパラメータを計算:式(3.140') mu_s_d = m_hat_d lambda_s_hat_dd = (1.0 - D + nu_hat) * beta_hat / (1 + beta_hat) * w_hat_dd nu_s_hat = 1.0 - D + nu_hat
予測分布のパラメータを
で計算して、結果をmu_s_hat_d、lambda_s_hat_dd、nu_s_hatとします。
# 確認 print(mu_s_d) print(lambda_s_hat_dd) print(nu_s_hat)
[20.00090437 49.56291415]
[[ 0.00164507 -0.0004231 ]
[-0.0004231 0.00270596]]
51.0
$\mathbf{X}$から$\hat{\boldsymbol{\mu}}_s,\ \hat{\boldsymbol{\Lambda}}_s,\ \hat{\nu}_s$を学習しているのが式からも分かります。
求めたパラメータを用いて、予測分布の確率密度を計算します。
# 予測分布を計算:式(3.121)
predict = multivariate_t.pdf(
x=x_point_arr, loc=mu_s_d, shape=np.linalg.inv(lambda_s_hat_dd), df=nu_s_hat
)
尤度のときと同様に、x_point_arrの値ごとに確率密度を計算します。
計算結果は次のようになります。
# 確認 print(predict)
[5.61905221e-07 5.73829096e-07 5.85947323e-07 ... 2.49520970e-07
2.43607310e-07 2.37812117e-07]
予測分布を尤度と重ねて作図します。
# 予測分布を作図 plt.figure(figsize=(12, 9)) plt.contour(x_0_grid, x_1_grid, true_model.reshape(x_dims), alpha=0.5, linestyles='--') # 真の分布 plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真のmu plt.scatter(x=x_nd[:, 0], y=x_nd[:, 1]) # 観測データ plt.contour(x_0_grid, x_1_grid, predict.reshape(x_dims)) # 予測分布 plt.ylabel('$x_2$') plt.suptitle("Multivariate Student's t Distribution", fontsize=20) plt.title('$N=' + str(N) + ', \hat{\mu}_s=[' + ', '.join([str(mu) for mu in np.round(mu_s_d, 1)]) + ']' + ', \hat{\Lambda}_s=' + str([list(lmd_d) for lmd_d in np.round(lambda_s_hat_dd, 5)]) + ', \hat{\\nu}_s=' + str(nu_s_hat) + '$', loc='left') plt.colorbar() plt.show()
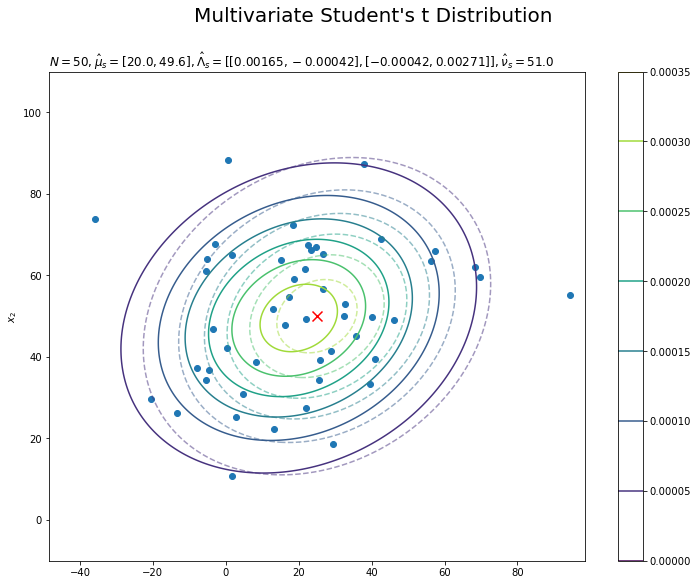
観測データが増えると、予測分布が真の分布に近づきます。
・おまけ:アニメーションで推移の確認
animationモジュールを利用して、事後分布と予測分布の推移をアニメーション(gif画像)で確認するためのコードです。
・コード(クリックで展開)
異なる点のみを簡単に解説します。
・ライブラリの読み込み
# 3.4.3項で利用するライブラリ import numpy as np from scipy.stats import multivariate_normal, multivariate_t # 多次元ガウス分布, 多次元スチューデントのt分布 import matplotlib.pyplot as plt import matplotlib.animation as animation
・モデルの設定
# 真の平均パラメータを指定 mu_truth_d = np.array([25.0, 50.0]) # (既知の)分散共分散行列を指定 sigma2_truth_dd = np.array([[600.0, 100.0], [100.0, 400.0]]) # (既知の精度)行列を計算 lambda_truth_dd = np.linalg.inv(sigma2_truth_dd) # muの事前分布のパラメータを指定 m_d = np.array([0.0, 0.0]) beta = 1 # lambdaの事前分布のパラメータを指定 nu = 2 w_dd = np.array([[0.0005, 0], [0, 0.0005]]) inv_w_dd = np.linalg.inv(w_dd) # 初期値による予測分布のパラメータを計算:式(3.140) mu_s_d = m_d lambda_s_dd = (nu - 1.0) * beta / (1 + beta) * w_dd nu_s = nu - 1.0
事前分布のパラメータを用いて、予測分布のパラメータを計算しておきます。
・作図用の点の作成
# 作図用のmuのx軸の値を作成 mu_0_line = np.linspace( mu_truth_d[0] - 2 * np.sqrt(np.linalg.inv(beta * nu * w_dd)[0, 0]), mu_truth_d[0] + 2 * np.sqrt(np.linalg.inv(beta * nu * w_dd)[0, 0]), num=500 ) # 作図用のmuのy軸の値を作成 mu_1_line = np.linspace( mu_truth_d[1] - 2 * np.sqrt(np.linalg.inv(beta * nu * w_dd)[1, 1]), mu_truth_d[1] + 2 * np.sqrt(np.linalg.inv(beta * nu * w_dd)[1, 1]), num=500 ) # 格子状の点を作成 mu_0_grid, mu_1_grid = np.meshgrid(mu_0_line, mu_1_line) # muの点を作成 mu_point_arr = np.stack([mu_0_grid.flatten(), mu_1_grid.flatten()], axis=1) mu_dims = mu_0_grid.shape # 作図用のxのx軸の値を作成 x_0_line = np.linspace( mu_truth_d[0] - 3 * np.sqrt(sigma2_truth_dd[0, 0]), mu_truth_d[0] + 3 * np.sqrt(sigma2_truth_dd[0, 0]), num=500 ) # 作図用のxのx軸の値を作成 x_1_line = np.linspace( mu_truth_d[1] - 3 * np.sqrt(sigma2_truth_dd[1, 1]), mu_truth_d[1] + 3 * np.sqrt(sigma2_truth_dd[1, 1]), num=500 ) # 格子状のxの値を作成 x_0_grid, x_1_grid = np.meshgrid(x_0_line, x_1_line) # xの点を作成 x_point_arr = np.stack([x_0_grid.flatten(), x_1_grid.flatten()], axis=1) x_dims = x_0_grid.shape
・推論処理
各試行の結果をリストに格納していく必要があります。$\mu$の事後分布をtrace_posterior、予測分布をtrace_predict、各パラメータをtrace_***として、初期値の結果を持つように作成しておきます。
# データ数(試行回数)を指定 N = 100 # 観測データの受け皿を作成 x_nd = np.empty((N, 2)) # 推移の記録用の受け皿を初期化 trace_m = [m_d] trace_beta = [beta] trace_posterior = [ multivariate_normal.pdf( x=mu_point_arr, mean=m_d, cov=np.linalg.inv(beta * nu * w_dd) ) ] trace_mu_s = [mu_s_d] trace_lambda_s = [lambda_s_dd] trace_nu_s = [nu_s] trace_predict = [ multivariate_t.pdf( x=x_point_arr, loc=mu_s_d, shape=np.linalg.inv(lambda_s_dd), df=nu_s ) ] # ベイズ推論 for n in range(N): # 多次元ガウス分布に従うデータを生成 x_nd[n] = np.random.multivariate_normal( mean=mu_truth_d, cov= np.linalg.inv(lambda_truth_dd) ).flatten() # muの事後分布のパラメータを:式(3.129) old_beta = beta old_m_d = m_d.copy() beta += 1 m_d = (x_nd[n] + old_beta * m_d) / beta # lambdaの事後分布のパラメータを更新:式(1.33) term_x_dd = np.dot(x_nd[n].reshape([2, 1]), x_nd[n].reshape([1, 2])) old_term_m_dd = old_beta * np.dot(old_m_d.reshape([2, 1]), old_m_d.reshape([1, 2])) term_m_dd = beta * np.dot(m_d.reshape([2, 1]), m_d.reshape([1, 2])) inv_w_dd += term_x_dd + old_term_m_dd - term_m_dd nu += 1 # muの事後分布を計算:式(2.72) trace_posterior.append( multivariate_normal.pdf( x=mu_point_arr, mean=m_d, cov=np.linalg.inv(beta * nu * np.linalg.inv(inv_w_dd)) ) ) # 予測分布のパラメータを更新:式(3.140) mu_s_d = m_d lambda_s_dd = (nu - 1.0) * beta / (1 + beta) * np.linalg.inv(inv_w_dd) nu_s = nu - 1.0 # 予測分布を計算:式(3.121) trace_predict.append( multivariate_t.pdf( x=x_point_arr, loc=mu_s_d, shape=np.linalg.inv(lambda_s_dd), df=nu_s ) ) # n回目の結果を記録 trace_m.append(m_d) trace_beta.append(beta) trace_mu_s.append(mu_s_d) trace_lambda_s.append(lambda_s_dd) trace_nu_s.append(nu_s) # 動作確認 #print('n=' + str(n + 1) + ' (' + str(np.round((n + 1) / N * 100, 1)) + '%)')
観測された各データによってどのように学習する(分布が変化する)のかを確認するため、for文で1データずつ処理します。よって、データ数Nがイタレーション数になります。
一度の処理で事後分布のパラメータを計算するのではなく、事前分布(1ステップ前の事後分布)に対して繰り返し観測データの情報を与えることでパラメータを更新(上書き)していきます。
それに伴い、事後分布のパラメータの計算式(3.129)、(3.133)の$\sum_{n=1}^N \mathbf{x}_n$や$N$の計算は、ループ処理によって$N$回繰り返しx_nd[n]と1を加えることで行います。$n$回目のループ処理のときには、$n-1$回分のx_nd[n]と1が既にm_d, w_ddとbeta, nuに加えられているわけです。
ただし、事後分布のパラメータの計算において更新前(1ステップ前)のパラメータを使うため、old_m_d, old_betaとして値を一時的に保存しておきます。
・事後分布の推移
# 画像サイズを指定 fig = plt.figure(figsize=(9, 9)) # 作図処理を関数として定義 def update_posterior(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目のmuの事後分布を作図 plt.contour(mu_0_grid, mu_1_grid, trace_posterior[n].reshape(mu_dims)) # muの事後分布 plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真の値 plt.xlabel('$\mu_1$') plt.ylabel('$\mu_2$') plt.suptitle('Multivariate Gaussian Distribution', fontsize=20) plt.title('$n=' + str(n) + ', \hat{\\beta}=' + str(trace_beta[n]) + ', \hat{m}=[' + ', '.join([str(m) for m in np.round(trace_m[n], 1)]) + ']' + '$', loc='left') # gif画像を作成 posterior_anime = animation.FuncAnimation(fig, update_posterior, frames=N + 1, interval=100) posterior_anime.save("ch3_4_3_Posterior.gif")
各フレーム(各試行)におけるパラメータの値をタイトルとして表示しています。ややこしければ、plt.title('n=' + str(n), loc='left')として試行回数だけ表示するだけでもそれっぽくなります。
初期値(事前分布)を含むため、フレーム数の引数nframesはN + 1です。
・予測分布の推移
# 尤度を計算:式(2.72) true_model = multivariate_normal.pdf( x=x_point_arr, mean=mu_truth_d, cov=np.linalg.inv(lambda_truth_dd) ) # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_predict(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目の予測分布を作図 plt.contour(x_0_grid, x_1_grid, true_model.reshape(x_dims), alpha=0.5, linestyles='--') # 真の分布 plt.scatter(x=mu_truth_d[0], y=mu_truth_d[1], color='red', s=100, marker='x') # 真のmu plt.scatter(x=x_nd[:n, 0], y=x_nd[:n, 1]) # 観測データ plt.contour(x_0_grid, x_1_grid, trace_predict[n].reshape(x_dims)) # 予測分布 plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.suptitle("Multivariate Student's t Distribution", fontsize=20) plt.title('$N=' + str(n) + ', \hat{\mu}_s=[' + ', '.join([str(mu) for mu in np.round(trace_mu_s[n], 1)]) + ']' + ', \hat{\Lambda}_s=' + str([list(lmd_d) for lmd_d in np.round(trace_lambda_s[n], 5)]) + ', \hat{\\nu}_s=' + str(trace_nu_s[n]) + '$', loc='left') # gif画像を作成 predict_anime = animation.FuncAnimation(fig, update_predict, frames=N + 1, interval=100) predict_anime.save("ch3_4_3_Predict.gif")
(よく理解していないので、animationの解説は省略…とりあえずこれで動きます……)
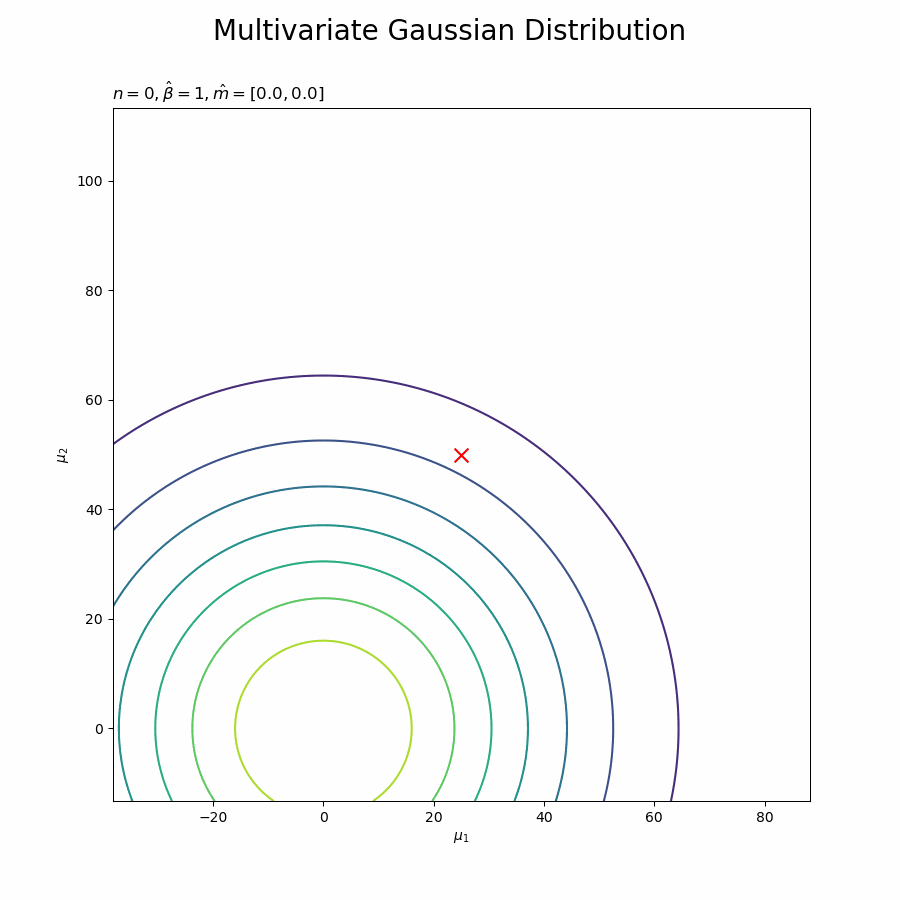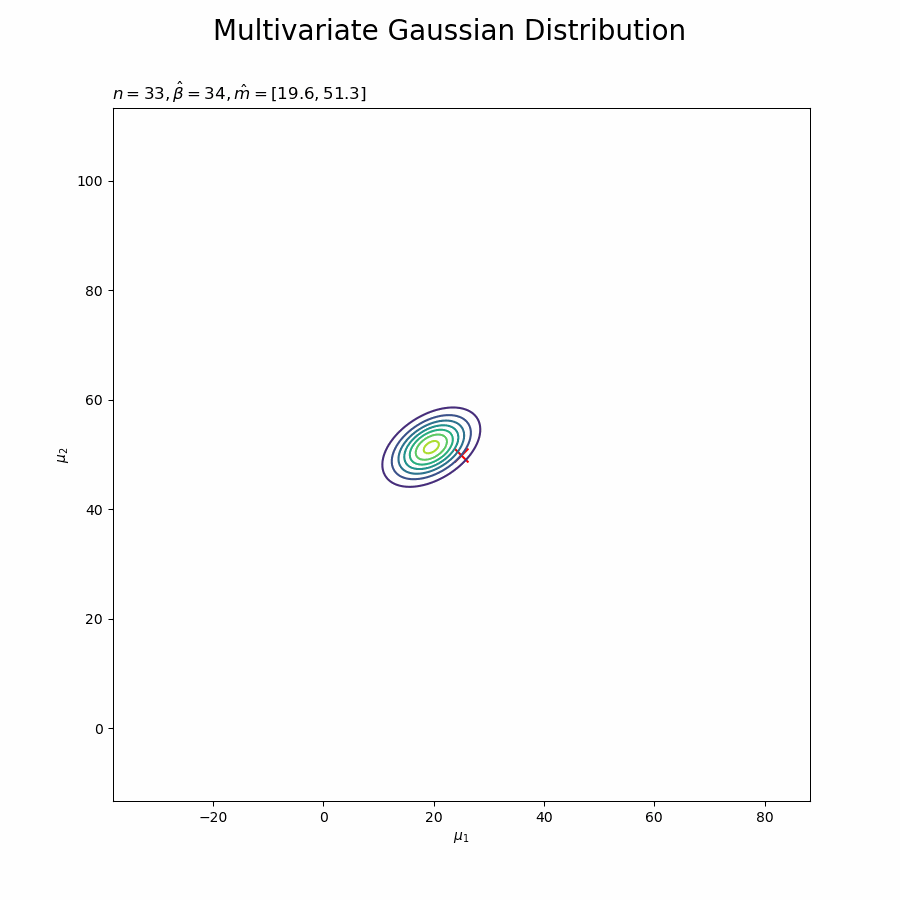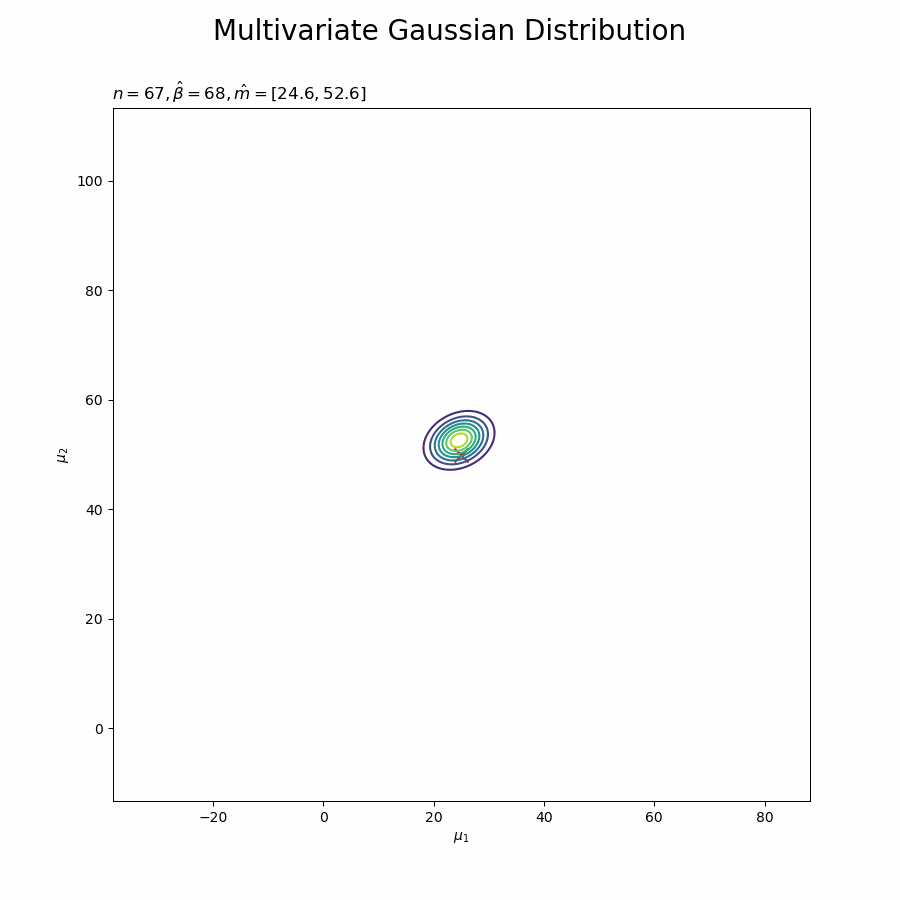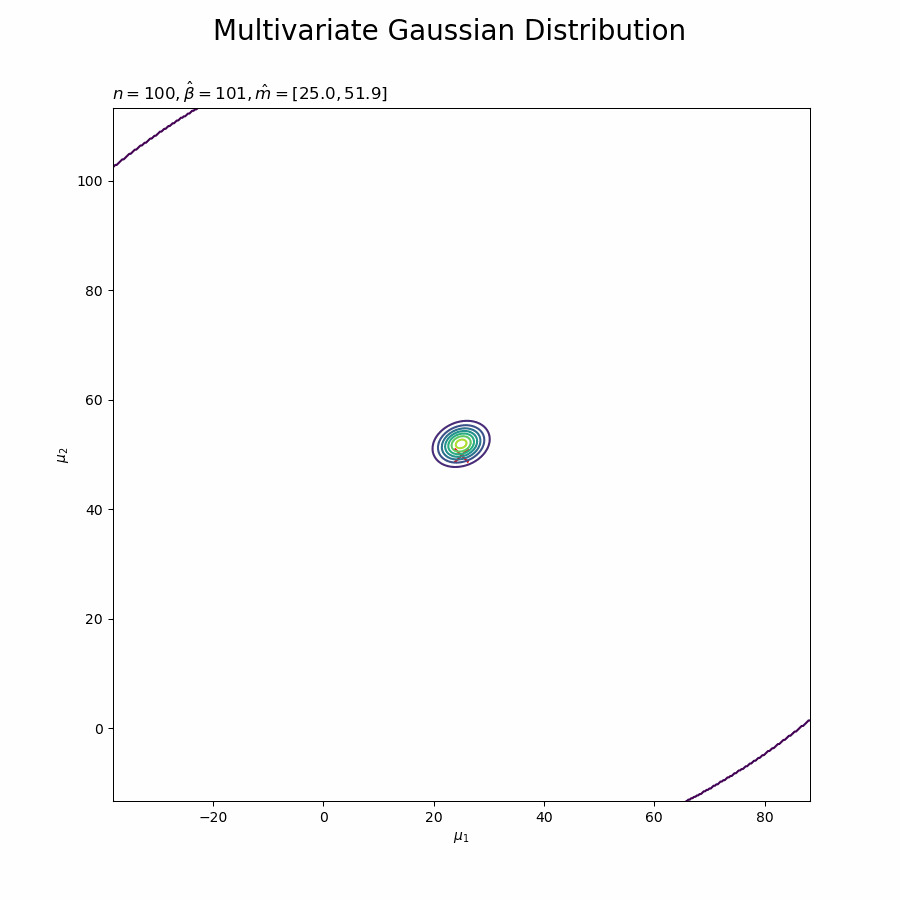
データが増えるに従って先が尖っていきます。
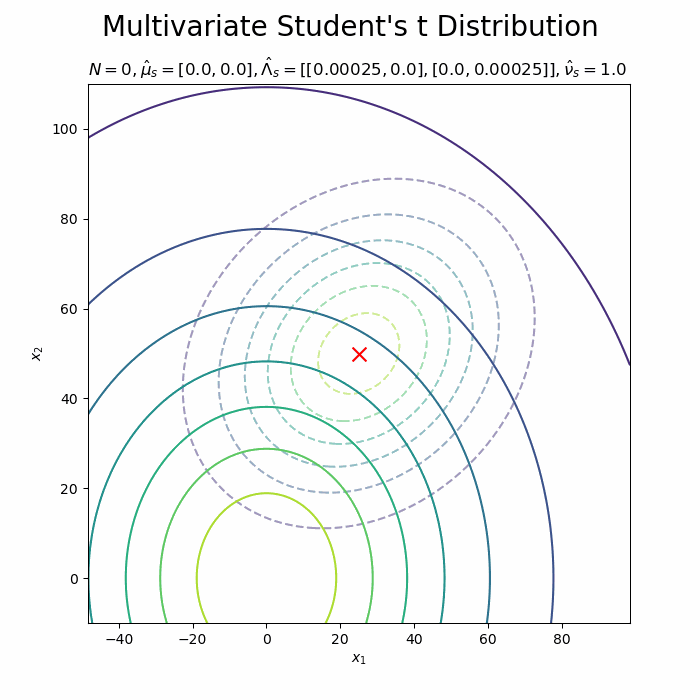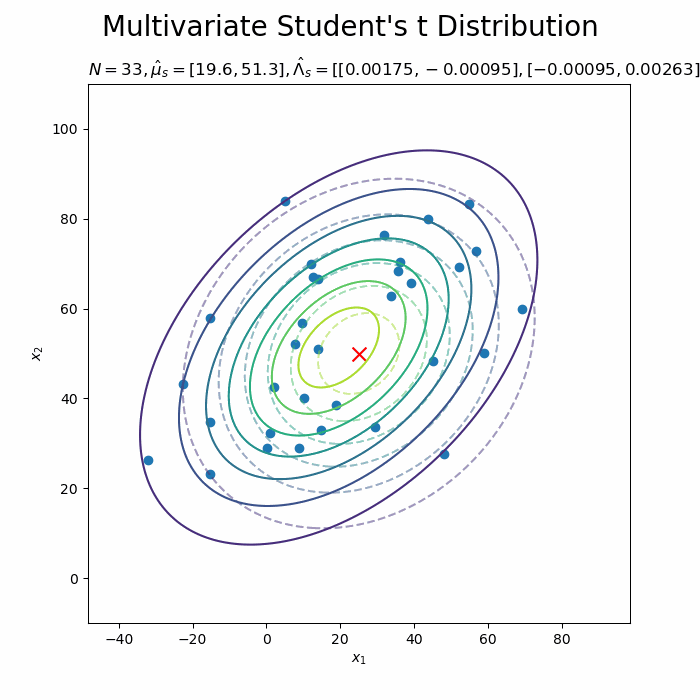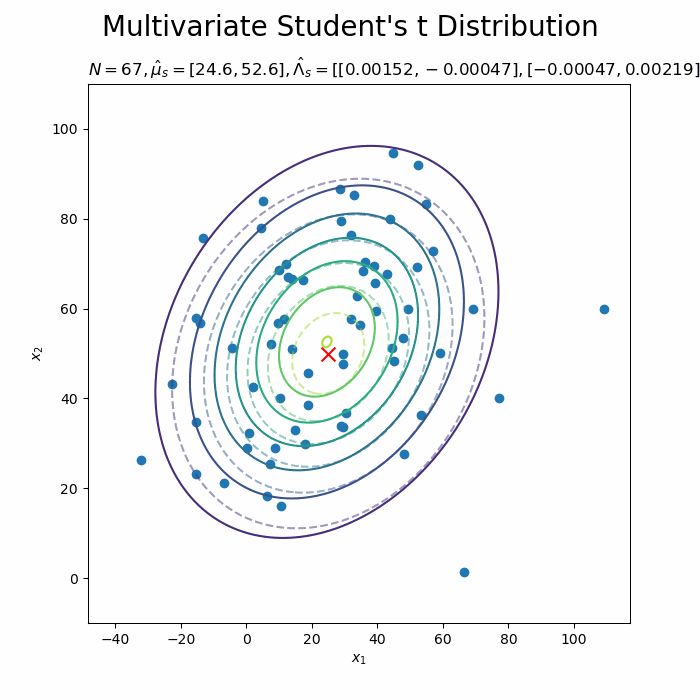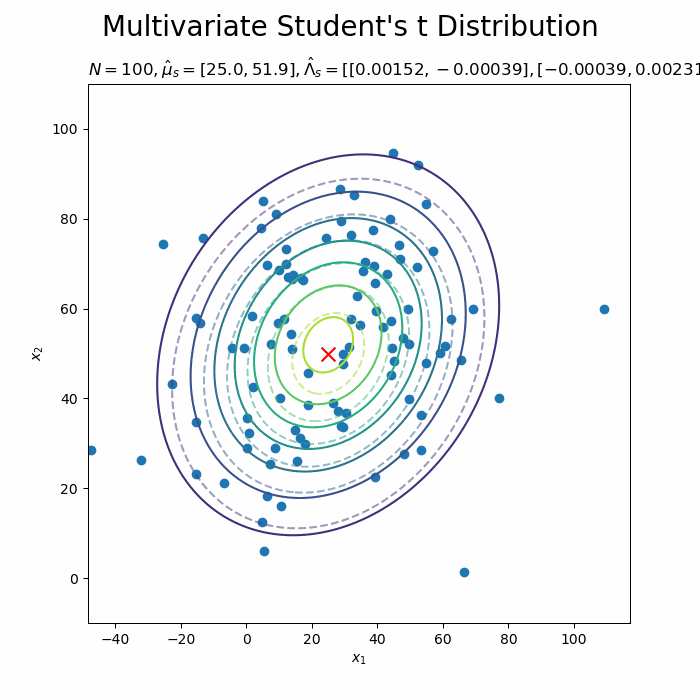
新たなデータによって平均(分布の中心)と精度(分布の広がり)が推移しているのを確認できます。
参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
この節の修正とPythonでの実装をしてる間に、SciPyに多次元版のスチューデントのt分布のモジュールが実装されて歓喜した。
2021年4月12日は、元℃-ute・元Buono!の鈴木愛理さんの27歳のお誕生日です!おめでとうございます!
ほんと素敵な方です。ぜひ見て!聴いて!ください。
【次節の内容】