はじめに
『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本の内容を1つずつ確認しながらゆっくりと組んでいきます。
この記事は、1.1節「数学とPythonの復習」と1.2節「ニューラルネットワークの推論」の内容です。ニューラルネットワークの推論(順伝播)処理を説明して、Pythonで実装します。
【前巻の内容】
【他の節の内容】
【この節の内容】
1.1 数学とPythonの復習
1.1.1 ベクトルと行列
NumPyライブラリを読み込みます。
# NumPyをインポート import numpy as np
NumPy配列のベクトルを作成します。
# ベクトルを作成 x = np.array([1, 2, 3]) # クラス名を取得 print(x.__class__) # 各次元の要素数(配列の形状)を取得 print(x.shape) # 次元数を取得 print(x.ndim)
<class 'numpy.ndarray'>
(3,)
1
NumPy配列のことをndarrayとも呼びます。
NumPy配列の行列を作成します。
# 行列を作成 W = np.array([[1, 2, 3], [4, 5, 6]]) # クラス名を取得 print(W.__class__) # 各次元の要素数(配列の形状)を取得 print(W.shape) # 次元数を取得 print(W.ndim)
<class 'numpy.ndarray'>
(2, 3)
2
ベクトルのことを1次元配列、行列のことを2次元配列とも呼びます。これは要素が、ベクトルは横(または縦)に一方向(1次元)に、行列は縦と横の二方向(2次元)に並んでいることに対応します。また要素数が$n$のベクトルを$n$次元ベクトルと呼ぶこともあるので、注意してください。この資料では、次元は配列の形状(構造)を示す意味として統一し、$n$次元ベクトルではなく要素数$n$のベクトルといった表現をします。ただし、要素数が$n$のベクトルを$1 \times n$の行列と表現することもあります。
1.1.4 ベクトルの内積と行列の積
この項の内容は「行列の積」を参照ください。
1.2 ニューラルネットワークの推論
1.2.1 ニューラルネットワークの推論の全体図
・全結合層(Affineレイヤ)
入力を$\mathbf{x}$、重みを$\mathbf{W}$、バイアスを$\mathbf{b}$とします。それぞれ形状を
とします。
この資料では、Pythonの添字(インデックス)が0から始まるのに対応するため、数式の添字も0から始めることにします。
またこれらによって求められる隠れ層のニューロンを$\mathbf{h}$を
とします。
中間層の4つのニューロンは、それぞれ次のように計算します。
これを重み付き和と呼びます。
この4つの計算式は行列の積と行列の和の計算でひとまとめにできます。
このように、行列(の計算)として扱うのは「便利」で「楽」なんです。
この計算をNumPyで行ってみましょう。ここでは、値ではなく行列の形状に注目します。
## 全結合層の計算 # 入力を生成 x = np.random.randn(1, 2) print(x.shape) # 重みを生成 W = np.random.randn(2, 4) print(W.shape) # バイアスを生成 b = np.random.randn(1, 4) print(b.shape) # 隠れ層のニューロンを計算 h = np.dot(x, W) + b print(h.shape)
(1, 2)
(2, 4)
(1, 4)
(1, 4)
続いてバッチデータを扱う場合を考えます。バッチサイズを$N$とします。
# バッチサイズを指定 N = 10 ## 全結合層の計算 # 入力を生成 x = np.random.randn(N, 2) print(x.shape) # 重みを生成 W = np.random.randn(2, 4) print(W.shape) # バイアスを生成 b = np.random.randn(1, 4) print(b.shape) # 隠れ層のニューロンを計算 h = np.dot(x, W) + b print(h.shape)
(10, 2)
(2, 4)
(1, 4)
(10, 4)
行列の積の計算では、1つ目の列数と2つ目の行数が同じである必要があります。またその計算結果は、1つ目の行数、2つ目の列数の行列になります。
行列の和の計算では、同じ形状の行列である必要があります。計算結果も同じ形状になります。
全結合層によって変換したデータは、次に活性化を行います。次は活性化関数として利用されるシグモイド関数について確認します。
・シグモイド関数
シグモイド関数とは、次の式です。
シグモイド関数は、任意の実数を受け取り、0から1の実数を出力します。
では実装しましょう。
# シグモイド関数の実装 def sigmoid(x): return 1 / (1 + np.exp(-x))
実装したシグモイド関数で、先ほど計算した中間層のニューロンhを活性化(変換)してみましょう。
# シグモイド関数による活性化 a = sigmoid(h) print(np.round(h, 3)) print(np.round(a, 3)) print(a.shape)
[[ 3.326 0.035 6.168 1.646]
[-1.374 2.098 -2.913 -2.955]
[ 1.301 -0.016 2.174 1.564]
[ 0.493 -0.129 0.573 1.72 ]
[ 2.214 -0.319 3.946 2.26 ]
[-1.477 -0.144 -3.309 1.569]
[ 0.202 0.573 0.06 0.273]
[-1.79 0.375 -3.883 0.491]
[ 1.971 0.288 3.521 1.011]
[ 1.413 0.731 2.459 0.064]]
[[0.965 0.509 0.998 0.838]
[0.202 0.891 0.052 0.049]
[0.786 0.496 0.898 0.827]
[0.621 0.468 0.639 0.848]
[0.901 0.421 0.981 0.906]
[0.186 0.464 0.035 0.828]
[0.55 0.639 0.515 0.568]
[0.143 0.593 0.02 0.62 ]
[0.878 0.571 0.971 0.733]
[0.804 0.675 0.921 0.516]]
(10, 4)
入力した要素間の大小関係は保ちつつ、0以上1以下の値に変換されました。
活性化されたデータのことをアクティベーションと呼びます。
続いてシグモイド関数のグラフを描いてみましょう。作図にはMatplotlibライブラリを利用します。
# Matplotlibをインポート import matplotlib.pyplot as plt
x軸の値を生成して、シグモイド関数で変換し、グラフにします。
# x軸の値を生成 x = np.arange(-5, 5, 0.1) # シグモイド関数の計算 y = sigmoid(x) # 作図 plt.plot(x, y) # 点の位置 plt.hlines(y=0.5, xmin=np.min(x), xmax=np.max(x), linestyle='--', linewidth=1) # 水平線 plt.vlines(x=0, ymin=0, ymax=1, linestyle='--', linewidth=1) # 垂直線 plt.xlabel('x') # x軸ラベル plt.ylabel('y') # y軸ラベル plt.title('Sigmoid Function', fontsize=20) # タイトル plt.show() # 描画
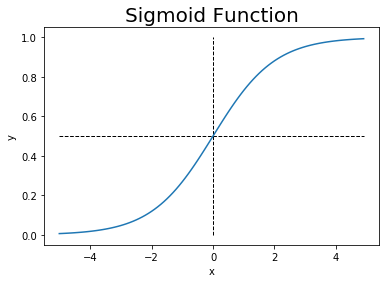
S字型のカーブを描きます。x軸の値が大きくなるほどy軸の値も大きくなることから、入力の大小関係が維持されることが分かります。
これで全結合のニューラルネットワークの基本となる処理を確認できました。次は最小サイズのニューラルネットワークの処理を行います。
・2層の全結合のニューラルネットワークの推論
2層のニューラルネットワークの計算を行います。
# バッチサイズを指定 N = 10 # 入力を生成 x = np.random.randn(N, 2) # 第1層のパラメータを生成 W1 = np.random.randn(2, 4) b1 = np.random.randn(1, 4) # 第2層のパラメータを生成 W2 = np.random.randn(4, 3) b2 = np.random.randn(1, 3) # 第1層の重み付き和の計算 h = np.dot(x, W1) + b1 # 第1層の活性化 a = sigmoid(h) # 第2層の重み付き和の計算 s = np.dot(a, W2) + b2 print(h.shape) print(a.shape) print(s.shape)
(10, 4)
(10, 4)
(10, 3)
活性化関数での変換ではデータの形状は変わりません。これは図1-7のニューロンの数からも分かります。
この出力(Softmax関数による正規化を行う前の値)をスコアと呼びます。このスコアが高いほど正規化後の(確率と解釈できる)値も高くなります。つまりスコアが高いクラスとなる確率が高いことが分かります。
次は。ここで行った処理をレイヤとしてクラスを使って実装します。
1.2.2 レイヤとしてのクラス化と順伝播の実装
クラスについては1巻のレジュメを参照ください。
Sigmoidレイヤ(の順伝播)を実装します。
# Sigmoidレイヤの実装 class Sigmoid: # 初期化メソッドの定義 def __init__(self): self.params = [] # パラメータ # 順伝播メソッドの定義 def forward(self, x): return 1 / (1 + np.exp(-x)) # 式(1.5)
Sigmoidレイヤではパラメータがないため、インスタンス変数を空のリスト[]として定義します。
続いてAffineレイヤ(の順伝播)を実装します。
# Affinレイヤの実装 class Affine: # 初期化メソッドの定義 def __init__(self, W, b): self.params = [W, b] # パラメータ # 順伝播メソッドの定義 def forward(self, x): W, b = self.params out = np.dot(x, W) + b # 式(1.4) return out
AffineレイヤとSigmoidレイヤを用いて、2層の全結合ニューラルネットワークの処理を行います。
まずは各変数を作成します。
# バッチサイズを指定 N = 10 # 入力を生成 x = np.random.randn(N, 2) # 第1層のパラメータ W1 = np.random.randn(2, 4) b1 = np.random.randn(1, 4) # 第2層のパラメータ W2 = np.random.randn(4, 3) b2 = np.random.randn(1, 3)
ニューラルネットワークを構成する各レイヤのクラスを図1-11の順番にリストにまとめます。
# 各レイヤをリストに格納 layers = [ Affine(W1, b1), Sigmoid(), Affine(W2, b2) ] print(layers)
[<__main__.Affine object at 0x0000021FA7ABE348>, <__main__.Sigmoid object at 0x0000021FA75700C8>, <__main__.Affine object at 0x0000021FA7ABE388>]
for文で、リストに格納した各クラスの順伝播メソッドを実行します。
# 各レイヤの順伝播メソッドを実行 for layer in layers: x = layer.forward(x) print(x.shape)
(10, 4)
(10, 4)
(10, 3)
これが前項と同じ処理になります。
ではこの処理をクラスとしてまとめて、2層の全結合ニューラルネットワークを実装します。
# 2層の全結合ニューラルネットワークの実装 class TwoLayerNet: # 初期化メソッドの定義 def __init__(self, input_size, hidden_size, output_size): # 各レイヤのニューロン数を受け取る I, H, O = input_size, hidden_size, output_size # 各レイヤの重みとバイアスの初期値を生成 W1 = np.random.randn(I, H) b1 = np.random.randn(H) W2 = np.random.randn(H, O) b2 = np.random.randn(O) # レイヤを生成 self.layers = [ Affine(W1, b1), Sigmoid(), Affine(W2, b2) ] # 各レイヤのパラメータのリストを結合 self.params = [] # 初期化 for layer in self.layers: self.params += layer.params # 推論メソッドの定義 def predict(self, x): # 各レイヤの順伝播を実行 for layer in self.layers: x = layer.forward(x) return x
パラメータを格納したリストの結合には、+によるリストの結合を利用しています。
fruit_1 = ['ピーチ', 'りんご'] fruit_2 = ['レモン', 'オレンジ'] fruit_3 = ['ブドウ', 'メロン'] juice = fruit_1 + fruit_2 + fruit_3 print(juice)
['ピーチ', 'りんご', 'レモン', 'オレンジ', 'ブドウ', 'メロン']
実装したクラスを使って推論処理を行いましょう。
# バッチサイズを指定 N = 10 # 入力を生成 x = np.random.randn(N, 2) # ニューラルネットワークのインスタンスを作成 model = TwoLayerNet(input_size=2, hidden_size=4, output_size=3) # 推論処理 s = model.predict(x) print(s.shape)
(10, 3)
これまでの処理をクラスとしてまとめたことで、4行でスコアを求めることができました。
この節では、推論(順伝播メソッド)を扱いました。次節では、学習(逆伝播メソッド)を扱います。
参考文献
おわりに
ゼロつく2巻NLP編!やっていきます。1巻に引き続き順調に進められるといーな。まずはその1記事目です。
オープニング曲です♪♪Juice=Juiceで「初めてを経験中」(2013年)
奥が深く 時には難しい
【次節の内容】
