2.3：収益と状態価値関数【ゼロつく4のノート】

はじめに

　『ゼロから作るDeep Learning 4 ――強化学習編』の独学時のまとめノートです。初学者の補助となるようにゼロつくシリーズの4巻の内容に解説を加えていきます。本と一緒に読んでください。

　この記事は、2.3節の内容です。割引累積報酬と状態価値関数の定義式を確認します。

【前節の内容】

www.anarchive-beta.com

【他の記事一覧】

www.anarchive-beta.com

【この記事の内容】

2.3 MDPの目標

　MDPについては本を読んでください。

2.3.2 収益

　ここまでは、ある時刻における報酬を考えました。この節では、ある時刻以降の全ての報酬(将来の報酬)を考えます。

　利用するライブラリを読み込みます。

# 利用するライブラリ
import numpy as np
import matplotlib.pyplot as plt

・定義式の確認

　まずは、収益の定義を確認します。

　時刻$t$における収益$G_t$は、割引率$\gamma$を用いて、次の式で定義されます。

$$ G_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots \tag{2.1} $$

　$\gamma$は、0から1の値を設定します。
　収益のことを割引累積報酬などとも呼ばれます。将来の報酬を現在(時刻$t$)時点における価値に割り引いた総和と言えます。

　ちなみに、0乗は1になるので($x^0 = 1$なので)、次のようにまとめられます。

$$ G_t = \gamma^0 R_t + \gamma^1 R_{t+1} + \gamma^2 R_{t+2} + \cdots = \sum_{k=0}^{\infty} \gamma^{k} R_{t+k} $$

　$k$が大きいほど遠い将来を表します。

・グラフの確認

　次に、収益をグラフで確認します。

　分かりやすいように報酬を一定として、報酬と報酬の累積和の関係をグラフで確認します。

# 時間の最大値を指定
max_k = 10

# 一定の報酬を指定
r = 5

# K個の報酬を作成
R = np.repeat(r, max_k)

# 累積和を計算
G = np.cumsum(R)

# x軸の値を作成
k = np.arange(max_k)

# 収益のグラフを作成
plt.figure(figsize=(8, 6))
plt.plot(k, R, label='$R_{t+k}$') # 報酬
plt.plot(k, G, label='$G_t$') # 収益
plt.xlabel('k')
plt.ylabel('value')
plt.suptitle('$G_t = \sum_k\ R_{t+k}$', fontsize=20)
plt.title('r='+str(r)+'', loc='left')
plt.grid()
plt.legend()
plt.show()

累積報酬のグラフ

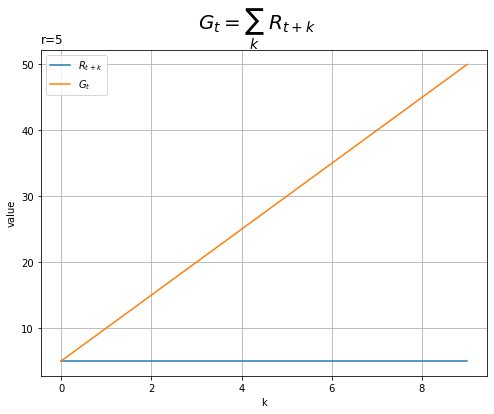
　将来に渡って報酬(青色の線)が一定です。そのため、累積和(オレンジ色の線)が一定に大きくなっています。

　続いて、割引率を導入して、報酬と収益(割引した報酬の累積和)の関係をグラフで確認します。

# 時間の最大値を指定
max_k = 10

# 一定の報酬を指定
r = 5

# K個の報酬を作成
R = np.repeat(r, max_k)

# 割引率を指定
gamma = 0.3

# x軸の値を作成
k = np.arange(max_k)

# 収益を計算
G = np.cumsum(gamma**k * R)

# 収益のグラフを作成
plt.figure(figsize=(8, 6))
plt.plot(k, gamma**k * R, label='$\gamma^k R_{t+k}$') # 報酬
plt.plot(k, G, label='$G_t$') # 収益
plt.plot(k, gamma**k, label='$\gamma^k$') # 割引率
plt.xlabel('k')
plt.ylabel('value')
plt.suptitle('$G_t = \sum_k\ \gamma^k R_{t+k}$', fontsize=20)
plt.title('$\gamma='+str(gamma) + ', r='+str(r)+'$', loc='left')
plt.grid()
plt.legend()
plt.show()

割引累積報酬のグラフ

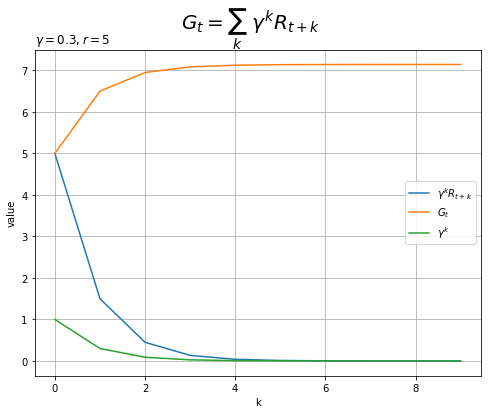
　将来の報酬に対する重み(緑色の線)$\gamma^k$がほとんど0になっています。そのため、将来の報酬の価値(青色の線)もほとんど0になります。よって、収益(オレンジ色の線)が収束します。

　最後に、割引率の累乗のグラフを確認します。

# 時間の最大値を指定
max_k = 10

# x軸の値を作成
k = np.arange(max_k)

# 割引率を指定
gamma_vals = [0.05, 0.1, 0.2, 0.4, 0.8]

# 割引率のグラフを作成
plt.figure(figsize=(8, 6))
for gamma in gamma_vals:
    plt.plot(k, gamma**k, label='$\gamma='+str(gamma)+'$') # 割引率
plt.xlabel('k')
plt.ylabel('$\gamma^k$')
plt.suptitle('Discount Rate', fontsize=20)
plt.grid()
plt.legend()
plt.show()

割引率のグラフ

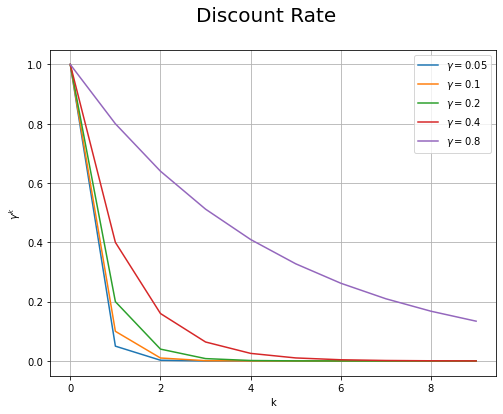
　割引率が大きいほど、遠い将来の($k$が大きい)報酬$R_{t+k}$に対する重みが大きくなり、将来の報酬に対する価値を高く評価するのが分かります。

2.3.3 状態価値関数

　前項では、収益(将来の報酬)を考えました。この項では、収益の期待値を考えます。

・定義式の確認

　状態価値関数の定義を確認します。

　時刻$t$において、状態$S_t$が$s$であり、確率的な方策$\pi(a | s)$を取るときの収益$G_t$の期待値を次の式で表します。

$$ v_{\pi}(s) = \mathbb{E}_{\pi}[G_t | S_t = s] \tag{2.3} $$

　この式を状態価値関数と呼びます。これは、現在(時刻$t$)の状態が$s$でありここから方策$\pi(a | s)$に従って行動を取り続けたときに見込まれる収益のことで、状態$s$に対する価値と言えます。

　ところで、状態価値の具体的な計算って、こんな感じでいいんですかね？よく分かりません。

$$ \begin{aligned} \mathbb{E}_{\pi}[G_t | S_t = s] &= \sum_{k=0}^{\infty} \sum_{s'} \sum_a \gamma^k r(S_{t+k} = s, A_{t+k} = a, S_{t+k+1} = s') \pi(A_{t+k} = a | S_{t+k} = s) p(S_{t+k+1} = s' | S_{t+k} = s, A_{t+k} = a) \\ &= \sum_{k=0}^{\infty} \sum_{s'} \sum_a \gamma^k r(S_{t+k} = s, A_{t+k} = a, S_{t+k+1} = s') p(S_{t+k+1} = s', A_{t+k} = a | S_{t+k} = s) \\ &= \sum_{k=0}^{\infty} \sum_{s'} \sum_a \gamma^k r(s, a, s') p(s', a | s) \\ &= \sum_{s'} \left\{ \sum_{k=0}^{\infty} \gamma^k R_{t+k} \right\} \left\{ \sum_a p(s', a | s) \right\} \\ &= \sum_{s'} G_t p(s' | s) \end{aligned} $$

　将来の報酬$R_{t+k}$のそれぞれ$k = 0, 1, \dots$に対して$s', a$の同時分布を用いて期待値をとって$k$について総和を求める必要があるが、方策・遷移確率・報酬関数は時刻$t + k$に依存しないので上手いこと式が整理されて、収益$G_t$を状態が$s$から$s'$に遷移する確率(not状態遷移確率)$p(s' | s)$で期待値を求めればよい？
　この収益の期待値を計算する(将来$k = 1, 2, \dots$について計算する)際の依存関係がよく分からず、次章の内容を理解し切れませんでした、、調べてもよく分からなかったので誰か教えてください。。。

　この章では、マルコフ決定過程における問題設定を確認しました。次章では、マルコフ決定過程の具体的な計算を確認します。

参考文献

• 斎藤康毅『ゼロから作るDeep Learning 4 ――強化学習編』オライリー・ジャパン,2022年.
• サポートページ：GitHub - oreilly-japan/deep-learning-from-scratch-4

おわりに

　依存関係がよく分かりません。実装まで進めば理解も進むのでしょうか。だといいな。

【次節の内容】

www.anarchive-beta.com

　状態価値関数その2は、次の次の記事で扱います。

www.anarchive-beta.com