はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語でガウス-ガンマ分布(正規-ガンマ分布)のグラフを作成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
ガウス-ガンマ分布の作図
ガウス-ガンマ分布(Gaussian-Gamma Distribution)または正規-ガンマ分布(Normal-Gamma Distribution)のグラフを作成します。ガウス-ガンマ分布については「ガウス-ガンマ分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
定義式の確認
まずは、ガウス-ガンマ分布の定義式を確認します。
ガウス-ガンマ分布は、1次元ガウス分布とガンマ分布の積で定義される$\mu, \lambda$の同時分布です。
ここで、$\mu$はガウス分布の確率変数で、$m$は平均パラメータ、$\beta$は精度パラメータの係数です。$\lambda$は精度に比例する値で、$\beta \lambda$が精度、精度の逆数$(\beta \lambda)^{-1} = \frac{1}{\beta \lambda}$が分散、分散の平方根$(\beta \lambda)^{-\frac{1}{2}} = \frac{1}{\sqrt{\beta \lambda}}$が標準偏差です。また、$\lambda$はガンマ分布の確率変数でもあり、$a$は形状パラメータ、$b$は尺度パラメータです。$\pi$は円周率、$\Gamma(x)$はガンマ関数です。
確率変数の値$\mu$は実数、$\lambda$は正の実数をとります。パラメータ$\lambda, \beta, a, b$はそれぞれ正の実数を満たす必要があります。
ガウス-ガンマ分布の$\mu$の平均と分散は、定義より次となります。
また、$\lambda$の平均・分散・最頻値は、次の式で計算できます。
これらの計算を行いグラフを作成します。
グラフの作成
ggplot2パッケージを利用して、ガウス-ガンマ分布のグラフを作成します。ガウス-ガンマ分布の確率密度や統計量の計算については「【R】ガウス-ガンマ分布の計算 - からっぽのしょこ」を参照してください。
ガウス-ガンマ分布のパラメータ$m, \beta, a, b$を設定します。
# 1次元ガウス分布の平均パラメータを指定 m <- 0 # 1次元ガウス分布の精度パラメータの係数を指定 beta <- 2 # ガンマ分布のパラメータを指定 a <- 5 b <- 6
ガウス分布の平均パラメータ$m$と精度パラメータの係数$\beta > 0$、ガンマ分布の形状パラメータ$a > 0$と尺度パラメータ$b > 0$を指定します。
ガウス分布の確率変数がとり得る値$\mu$とガンマ分布の確率変数がとり得る値$\lambda$を作成します。
# μの値を作成 mu_vals <- seq(from = -3, to = 3, length.out = 201) # λの値を作成 lambda_vals <- seq(from = 0, to = 2, length.out = 201) head(mu_vals); head(lambda_vals)
## [1] -3.00 -2.97 -2.94 -2.91 -2.88 -2.85 ## [1] 0.00 0.01 0.02 0.03 0.04 0.05
実数$\mu$の値を作成してmu_valsとします。この例では、-3から3を範囲とします。
正の実数$\lambda$の値を作成してlambda_valsとします。この例では、0から2を範囲とします。
ガウス-ガンマ分布の確率変数がとり得る値$(\mu, \lambda)$ごとの確率密度を計算します。
# ガウス-ガンマ分布を計算 dens_df <- tidyr::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals # 確率変数λ ) |> # 確率変数(μとλの格子点)を作成 dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens # 確率密度 ) dens_df
## # A tibble: 40,401 × 5 ## mu lambda N_dens Gam_dens density ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 -3 0 0 0 0 ## 2 -3 0.01 0.0516 0.00000305 0.000000157 ## 3 -3 0.02 0.0666 0.0000460 0.00000306 ## 4 -3 0.03 0.0746 0.000219 0.0000164 ## 5 -3 0.04 0.0787 0.000652 0.0000514 ## 6 -3 0.05 0.0804 0.00150 0.000121 ## 7 -3 0.06 0.0805 0.00293 0.000236 ## 8 -3 0.07 0.0795 0.00511 0.000406 ## 9 -3 0.08 0.0777 0.00821 0.000638 ## 10 -3 0.09 0.0753 0.0124 0.000933 ## # … with 40,391 more rows
$\mu$の値mu_valsと$\lambda$の値lambda_valsの要素の全ての組み合わせ($\mu$と$\lambda$の格子点)をexpand.grid()で作成します。組み合わせ(点$(\mu, \lambda)$)ごとに確率密度を計算します。
dnorm()の確率変数の引数xにmu_valsの値、平均の引数meanにm、標準偏差の引数sdにbetaとlambda_valsの値の積の平方根の逆数を指定して、ガウス分布の確率密度を計算します。
dgamma()の確率変数の引数xにlambda_valsの値、形状の引数shapeにa、尺度の引数rateにbを指定して、ガンマ分布の確率密度を計算します。
2つの確率密度の積を計算します。
ガウス-ガンマ分布のグラフを作成します。
# ガウス-ガンマ分布を作図 ggplot() + geom_contour(data = dens_df, aes(x = mu, y = lambda, z = density, color = ..level..)) + # 等高線 #geom_contour_filled(data = dens_df, aes(x = mu, y = lambda, z = density, fill = ..level..), # alpha = 0.8) + # 塗りつぶし等高線 labs( title = "Gaussian-Gamma Distribution", #subtitle = paste0("m=", m, ", beta=", beta, ", a=", a, ", b=", b), # (文字列表記用) subtitle = parse(text = paste0("list(m==", m, ", beta==", beta, ", a==", a, ", b==", b, ")")), # (数式表記用) color = "density", fill = "density", x = expression(mu), y = expression(lambda) ) # ラベル


geom_contour()で等高線図、geom_contour_filled()で塗りつぶし等高線図を描画できます。
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
この分布に統計量の情報を重ねて表示します。
$\mu$の期待値と標準偏差を計算します。
# μに関する統計量を格納 stat_mu_df <- tibble::tibble( lambda = lambda_vals, # 確率変数λ mean = m, # 期待値 sd = 1 / sqrt(beta * lambda_vals) # 標準偏差 ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !lambda, names_to = "group", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(group, pattern = "sd_.*", replacement = "sd") ) # 期待値±標準偏差のカテゴリを統一 stat_mu_df
## # A tibble: 603 × 4 ## lambda group statistic type ## <dbl> <chr> <dbl> <chr> ## 1 0 mean 0 mean ## 2 0 sd_minus -Inf sd ## 3 0 sd_plus Inf sd ## 4 0.01 mean 0 mean ## 5 0.01 sd_minus -7.07 sd ## 6 0.01 sd_plus 7.07 sd ## 7 0.02 mean 0 mean ## 8 0.02 sd_minus -5 sd ## 9 0.02 sd_plus 5 sd ## 10 0.03 mean 0 mean ## # … with 593 more rows
期待値・標準偏差を計算して、さらに期待値から標準偏差を引いた値と足した値を求めます。ガウス分布の期待値と最頻値は一致するので、最頻値を省略します。
期待値・標準偏差の和と差の3つの列をpivot_longer()でまとめます。列名がラベルになるので、そのままのラベル列groupと、標準偏差の和と差のラベルを統一したラベル列typeを用意します。
同様に、$\lambda$の期待値・標準偏差・最頻値を計算します。
# λに関する統計量を格納 stat_lambda_df <- tibble::tibble( mean = a / b, # 期待値 sd = sqrt(a / b^2), # 標準偏差 mode = (a - 1) / b # 最頻値 ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = dplyr::everything(), names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd") ) # 期待値±標準偏差のカテゴリを統一 stat_lambda_df
## # A tibble: 4 × 2 ## type statistic ## <chr> <dbl> ## 1 mean 0.833 ## 2 mode 0.667 ## 3 sd 0.461 ## 4 sd 1.21
こちらは、期待値・標準偏差の和と差・最頻値を計算して、4つの列をpivot_longer()でまとめます。
線の色や種類、凡例テキストを指定する場合は、設定用の名前付きベクトルを作成します。
# 凡例用の設定を作成:(数式表示用) color_vec <- c(mean = "blue", sd = "orange", mode = "chocolate") linetype_vec <- c(mean = "dashed", sd = "dotted", mode = "dashed") label_vec <- c(mean = expression(E(x)), sd = expression(E(x) %+-% sqrt(V(x))), mode = expression(mode(x))) color_vec; linetype_vec; color_vec
## mean sd mode ## "blue" "orange" "chocolate" ## mean sd mode ## "dashed" "dotted" "dashed" ## mean sd mode ## "blue" "orange" "chocolate"
各要素(設定)の名前をtype列の文字列と対応させて、設定(線の色・種類と数式用のテキスト)を指定します。
凡例付きのグラフを作成します。
# 統計量を重ねたガウス-ガンマ分布を作図 ggplot() + geom_contour_filled(data = dens_df, aes(x = mu, y = lambda, z = density, fill = ..level..), alpha = 0.8) + # 分布 geom_line(data = stat_mu_df, mapping = aes(x = statistic, y = lambda, color = type, linetype = type, group = group), size = 1) + # μの統計量 geom_hline(data = stat_lambda_df, mapping = aes(yintercept = statistic, color = type, linetype = type), size = 1) + # λの統計量 scale_linetype_manual(values = linetype_vec, labels = label_vec, name = "statistic") + # 線の種類:(線指定と数式表示用) scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(色指定と数式表示用) guides(color = guide_legend(override.aes = list(size = 0.5))) + # 凡例の体裁 theme(legend.text.align = 0) + # 図の体裁:凡例 coord_cartesian(xlim = c(min(mu_vals), max(mu_vals))) + # x軸の表示範囲 labs(title = "Gaussian-Gamma Distribution", subtitle = parse(text = paste0("list(m==", m, ", beta==", beta, ", a==", a, ", b==", b, ")")), color = "statistic", fill = "density", x = expression(mu), y = expression(lambda)) # ラベル
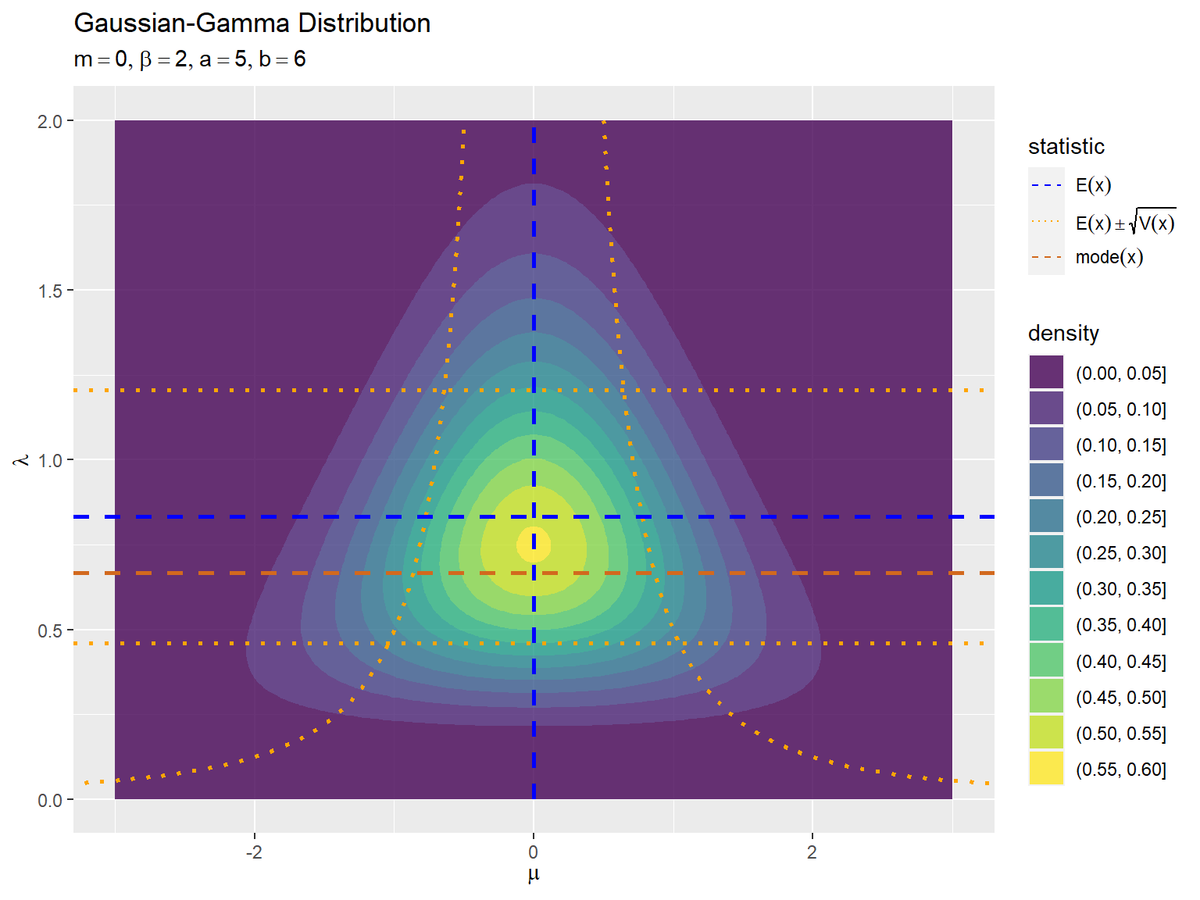
$\mu$に関する統計量はgeom_line()で折れ線として、$\lambda$に関する統計量はgeom_hline()で水平線として描画します。
ガウス分布の標準偏差は、$\lambda$の影響を受ける(計算式に$\lambda$を含む)ので、平均から標準偏差を足し引きした値(オレンジ色の点線)は$\lambda$(y軸)の値によって変化します。この曲線と、ガウス-ガンマ分布のおにぎり型の形状が対応しているのが分かります。
ガンマ分布($\lambda$に関する統計量)は、$\mu$の影響を受けない(定義式に$\mu$を含まない)ので、期待値・標準偏差・最頻値は一定(水平線)になります。また、ガンマ分布は非対称な形状なので、期待値(青色の破線)と最頻値(茶色の破線)が一致しません。
ガウス-ガンマ分布のグラフを描画できました。以降は、ここまでの作図処理を用いて、パラメータの影響を確認していきます。
1変数の形状をアニメーションで可視化
ガウス-ガンマ分布は2つの確率変数$\mu, \lambda$を持ちます。ここでは、それぞれの変数に注目して分布の形状を確認します。(上の図と合わせて3Dプロット感を出したかったのですが、思ったよりうまくいかなかったので飛ばしてください。)
μ軸側から見たグラフ
ガウス-ガンマ分布の$\mu$についての断面図(x軸から見たグラフ)と、$\mu$についての分布$\mathcal{N}(\mu | m, (\beta \lambda)^{-1})$のグラフを並べて比較します。ガウス分布については「【R】1次元ガウス分布の作図 - からっぽのしょこ」を参照してください。
・作図コード(クリックで展開)
ガウス-ガンマ分布を計算します。
# ガウス-ガンマ分布を計算 dens_df <- tidyr::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals # 確率変数λ ) |> # 確率変数(μとλの格子点)を作成 dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens, # 確率密度 parameter = paste0("lambda=", round(lambda, 2), ", m=", m, ", beta=", beta, ", a=", a, ", b=", b) |> factor(levels = paste0("lambda=", round(lambda_vals, 2), ", m=", m, ", beta=", beta, ", a=", a, ", b=", b)) # フレーム切替用ラベル ) dens_df
## # A tibble: 40,401 × 6 ## mu lambda N_dens Gam_dens density parameter ## <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -3 0 0 0 0 lambda=0, m=0, beta=2, a=5, b=6 ## 2 -3 0.01 0.0516 0.00000305 0.000000157 lambda=0.01, m=0, beta=2, a=5, b=6 ## 3 -3 0.02 0.0666 0.0000460 0.00000306 lambda=0.02, m=0, beta=2, a=5, b=6 ## 4 -3 0.03 0.0746 0.000219 0.0000164 lambda=0.03, m=0, beta=2, a=5, b=6 ## 5 -3 0.04 0.0787 0.000652 0.0000514 lambda=0.04, m=0, beta=2, a=5, b=6 ## 6 -3 0.05 0.0804 0.00150 0.000121 lambda=0.05, m=0, beta=2, a=5, b=6 ## 7 -3 0.06 0.0805 0.00293 0.000236 lambda=0.06, m=0, beta=2, a=5, b=6 ## 8 -3 0.07 0.0795 0.00511 0.000406 lambda=0.07, m=0, beta=2, a=5, b=6 ## 9 -3 0.08 0.0777 0.00821 0.000638 lambda=0.08, m=0, beta=2, a=5, b=6 ## 10 -3 0.09 0.0753 0.0124 0.000933 lambda=0.09, m=0, beta=2, a=5, b=6 ## # … with 40,391 more rows
lambda_valsの値ごとにフレーム切替用のラベルを作成します。
$\mu$についての統計量を計算します。
# μに関する統計量を格納 stat_mu_df <- tibble::tibble( lambda = lambda_vals, # 精度パラメータ mean = m, # 期待値 sd = 1 / sqrt(beta * lambda_vals) # 標準偏差 ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = !lambda, names_to = "group", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(group, pattern = "sd_.*", replacement = "sd"), # 期待値±標準偏差のカテゴリを統一 parameter = paste0("lambda=", round(lambda, 2), ", m=", m, ", beta=", beta, ", a=", a, ", b=", b) |> factor(levels = paste0("lambda=", round(lambda_vals, 2), ", m=", m, ", beta=", beta, ", a=", a, ", b=", b)) # フレーム切替用ラベル ) stat_mu_df
## # A tibble: 603 × 5 ## lambda group statistic type parameter ## <dbl> <chr> <dbl> <chr> <fct> ## 1 0 mean 0 mean lambda=0, m=0, beta=2, a=5, b=6 ## 2 0 sd_minus -Inf sd lambda=0, m=0, beta=2, a=5, b=6 ## 3 0 sd_plus Inf sd lambda=0, m=0, beta=2, a=5, b=6 ## 4 0.01 mean 0 mean lambda=0.01, m=0, beta=2, a=5, b=6 ## 5 0.01 sd_minus -7.07 sd lambda=0.01, m=0, beta=2, a=5, b=6 ## 6 0.01 sd_plus 7.07 sd lambda=0.01, m=0, beta=2, a=5, b=6 ## 7 0.02 mean 0 mean lambda=0.02, m=0, beta=2, a=5, b=6 ## 8 0.02 sd_minus -5 sd lambda=0.02, m=0, beta=2, a=5, b=6 ## 9 0.02 sd_plus 5 sd lambda=0.02, m=0, beta=2, a=5, b=6 ## 10 0.03 mean 0 mean lambda=0.03, m=0, beta=2, a=5, b=6 ## # … with 593 more rows
dens_dfと対応するようにフレーム切替用のラベルを作成します。
作図処理については次の「パラメータと分布の形状の関係」を参照してください。
$\mu$軸側から見たガウス-ガンマ分布の断面図とガウス分布のグラフのアニメーション(gif画像)を作成します。
# μ軸側から見たガウス-ガンマ分布を作図 dens_mu_graph <- ggplot() + geom_vline(data = stat_mu_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1, show.legend = FALSE) + # 統計量 geom_line(data = dens_df, mapping = aes(x = mu, y = density, color = "NG"), size = 1) + # ガウス-ガンマ分布 geom_line(data = dens_df, mapping = aes(x = mu, y = N_dens, color = "N"), size = 1) + # ガウス分布 gganimate::transition_manual(parameter) + # フレーム scale_color_manual(breaks = c("NG", "N", "mean", "sd"), values = c("#00A968", "purple", "blue", "orange"), labels = c("gaussian-gamma", "gaussian", expression(E(mu)), expression(E(mu) %+-% sqrt(V(mu)))), name = "distribution") + # 線の色 scale_linetype_manual(breaks = c("mean", "sd"), values = c("dashed", "dotted")) + # 線の種類 theme(legend.text.align = 0) + # 図の体裁:凡例 coord_cartesian(xlim = c(min(mu_vals), max(mu_vals))) + # 軸の表示範囲 labs(title = "Gaussian-Gamma Distribution", subtitle = "{current_frame}", x = expression(mu), y = "density") # gif画像を作成 gganimate::animate(dens_mu_graph, nframes = length(lambda_vals), fps = 10, width = 800, height = 600)

精度(に比例する値)$\lambda$が大きくなるほど、分散が小さくなり、ガウス分布(紫色の曲線)の山が細く高くなります。しかし、ガンマ分布の影響により、ガウス-ガンマ分布(青緑色の曲線)の山は徐々に小さくなります。
期待値から標準偏差を足し引きした値(オレンジ色の点線)が変化するのが、「グラフの作成」において曲線になるのに対応しています。
λ軸側から見たグラフ
続いて、$\lambda$についての断面図(y軸から見たグラフ)と、$\lambda$についての分布$\mathrm{Gam}(\lambda | a, b)$のグラフを並べて比較します。ガンマ分布については「【R】ガンマ分布の作図 - からっぽのしょこ」を参照してください。
・作図コード(クリックで展開)
ガウス-ガンマ分布を計算します。
# ガウス-ガンマ分布を計算 dens_df <- tidyr::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals # 確率変数λ ) |> # 確率変数(μとλの格子点)を作成 dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens, # 確率密度 parameter = paste0("mu=", round(mu, 2), ", m=", m, ", beta=", beta, ", a=", a, ", b=", b) |> factor(levels = paste0("mu=", round(mu_vals, 2), ", m=", m, ", beta=", beta, ", a=", a, ", b=", b)) # フレーム切替用ラベル ) dens_df
## # A tibble: 40,401 × 6 ## mu lambda N_dens Gam_dens density parameter ## <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -3 0 0 0 0 mu=-3, m=0, beta=2, a=5, b=6 ## 2 -3 0.01 0.0516 0.00000305 0.000000157 mu=-3, m=0, beta=2, a=5, b=6 ## 3 -3 0.02 0.0666 0.0000460 0.00000306 mu=-3, m=0, beta=2, a=5, b=6 ## 4 -3 0.03 0.0746 0.000219 0.0000164 mu=-3, m=0, beta=2, a=5, b=6 ## 5 -3 0.04 0.0787 0.000652 0.0000514 mu=-3, m=0, beta=2, a=5, b=6 ## 6 -3 0.05 0.0804 0.00150 0.000121 mu=-3, m=0, beta=2, a=5, b=6 ## 7 -3 0.06 0.0805 0.00293 0.000236 mu=-3, m=0, beta=2, a=5, b=6 ## 8 -3 0.07 0.0795 0.00511 0.000406 mu=-3, m=0, beta=2, a=5, b=6 ## 9 -3 0.08 0.0777 0.00821 0.000638 mu=-3, m=0, beta=2, a=5, b=6 ## 10 -3 0.09 0.0753 0.0124 0.000933 mu=-3, m=0, beta=2, a=5, b=6 ## # … with 40,391 more rows
mu_valsの値ごとにフレーム切替用のラベルを作成します。
$\lambda$についての統計量を計算します。
# λに関する統計量を格納 stat_lambda_df <- tibble::tibble( mean = a / b, # 期待値 sd = sqrt(a / b^2), # 標準偏差 mode = (a - 1) / b # 最頻値 ) |> # 統計量を計算 dplyr::mutate( sd_minus = mean - sd, sd_plus = mean + sd ) |> # 期待値±標準偏差を計算 dplyr::select(!sd) |> # 不要な列を削除 tidyr::pivot_longer( cols = dplyr::everything(), names_to = "type", values_to = "statistic" ) |> # 統計量の列をまとめる dplyr::mutate( type = stringr::str_replace(type, pattern = "sd_.*", replacement = "sd") ) # 期待値±標準偏差のカテゴリを統一 stat_lambda_df
## # A tibble: 4 × 2 ## type statistic ## <chr> <dbl> ## 1 mean 0.833 ## 2 mode 0.667 ## 3 sd 0.461 ## 4 sd 1.21
こちらは、$\mu$の影響を受けない(値が変化しない)ので、フレーム切替用のラベルは不要です。
$\lambda$軸側から見たガウス-ガンマ分布の断面図とガンマ分布のグラフのアニメーションを作成します。
# λ軸側から見たガウス-ガンマ分布を作図 dens_lambda_graph <- ggplot() + geom_vline(data = stat_lambda_df, mapping = aes(xintercept = statistic, color = type, linetype = type), size = 1, show.legend = FALSE) + # 統計量 geom_line(data = dens_df, mapping = aes(x = lambda, y = density, color = "NG"), size = 1) + # ガウス-ガンマ分布 geom_line(data = dens_df, mapping = aes(x = lambda, y = Gam_dens, color = "Gam"), size = 1) + # ガンマ分布 scale_color_manual(breaks = c("NG", "Gam", "mean", "sd", "mode"), values = c("#00A968", "purple", "blue", "orange", "chocolate"), labels = c("gaussian-gamma", "gaussian", expression(E(lambda)), expression(E(lambda) %+-% sqrt(V(lambda))), expression(mode(lambda))), name = "distribution") + # 線の色 scale_linetype_manual(breaks = c("mean", "sd", "mode"), values = c("dashed", "dotted", "dashed")) + # 線の種類 theme(legend.text.align = 0) + # 図の体裁:凡例 gganimate::transition_manual(parameter) + # フレーム labs(title = "Gaussian-Gamma Distribution", subtitle = "{current_frame}", x = expression(lambda), y = "density") # ラベル # gif画像を作成 gganimate::animate(dens_lambda_graph, nframes = length(mu_vals), fps = 10, width = 800, height = 600)

ガンマ分布(紫色の曲線)は$\mu$の影響を受けない(式に$\mu$を含まない)ので、変化しません。ガウス分布の影響によってガウス-ガンマ分布(青緑色の曲線)が変化します。
パラメータと分布の形状の関係をアニメーションで可視化
パラメータの値を少しずつ変化させて、分布の形状の変化をアニメーションで確認します。
mの影響
$m$の値を変化させ、$\beta, a, b$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータとして利用する値を作成 m_vals <- seq(from = -2, to = 2, by = 0.1) # 固定するパラメータを指定 beta <- 2 a <- 5 b <- 6 # 確率変数の値を作成 mu_vals <- seq(from = -3, to = 3, length.out = 201) lambda_vals <- seq(from = 0, to = 2, length.out = 201) # パラメータごとにガウス-ガンマ分布を計算 anime_dens_df <- tidyr:::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals, # 確率変数λ m = m_vals # パラメータm ) |> # 全ての組み合わせを作成 dplyr::arrange(m, mu, lambda) |> # パラメータごとに並べ替え dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens, # 確率密度 parameter = paste0("m=", round(m, 1), ", beta=", beta, ", a=", a, ", b=", b) |> factor(levels = paste0("m=", round(m_vals, 1), ", beta=", beta, ", a=", a, ", b=", b)) # フレーム切替用ラベル ) anime_dens_df
## # A tibble: 1,656,441 × 7 ## mu lambda m N_dens Gam_dens density parameter ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -3 0 -2 0 0 0 m=-2, beta=2, a=5, b=6 ## 2 -3 0.01 -2 0.0559 0.00000305 0.000000170 m=-2, beta=2, a=5, b=6 ## 3 -3 0.02 -2 0.0782 0.0000460 0.00000360 m=-2, beta=2, a=5, b=6 ## 4 -3 0.03 -2 0.0948 0.000219 0.0000208 m=-2, beta=2, a=5, b=6 ## 5 -3 0.04 -2 0.108 0.000652 0.0000707 m=-2, beta=2, a=5, b=6 ## 6 -3 0.05 -2 0.120 0.00150 0.000180 m=-2, beta=2, a=5, b=6 ## 7 -3 0.06 -2 0.130 0.00293 0.000381 m=-2, beta=2, a=5, b=6 ## 8 -3 0.07 -2 0.139 0.00511 0.000711 m=-2, beta=2, a=5, b=6 ## 9 -3 0.08 -2 0.147 0.00821 0.00121 m=-2, beta=2, a=5, b=6 ## 10 -3 0.09 -2 0.155 0.0124 0.00192 m=-2, beta=2, a=5, b=6 ## # … with 1,656,431 more rows
値の間隔が一定になるように$\mu$の値m_valsを作成します。パラメータごとにフレームを切り替えるので、m_valsの要素数がアニメーションのフレーム数になります。
確率変数mu_vals・lambda_vals・パラメータm_valsの要素の全ての組み合わせをexpand_grid()で作成します。
組み合わせごとに確率密度を計算して、パラメータごとにラベルを作成します。ラベルは、グラフを表示する順番を制御するのに使います。文字列型だと文字列の基準で順序が決まるので、因子型にしてパラメータに応じたレベル(順序)を設定します。
「mu_valsの要素数」掛ける「lambda_valsの要素数」掛ける「m_valsの要素数」行のデータフレームになります。行数が非常に多くなるので注意してください。
ガウス-ガンマ分布のアニメーション(gif画像)を作成します。
# ガウス-ガンマ分布のアニメーションを作図 anime_dens_graph <- ggplot() + geom_contour(data = anime_dens_df, aes(x = mu, y = lambda, z = density, color = ..level..)) + # 等高線 #geom_contour_filled(data = anime_dens_df, aes(x = mu, y = lambda, z = density, fill = ..level..), # alpha = 0.8) + # 塗りつぶし等高線 gganimate::transition_manual(parameter) + # フレーム labs(title = "Gaussian-Gamma Distribution", subtitle = "{current_frame}", color = "density", fill = "density", x = expression(mu), y = expression(lambda)) # gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(m_vals), fps = 10, width = 800, height = 600)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにパラメータ数、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと意図通りに動作しません。


$\mu$(ガウス分布)の期待値が$m$なので、$\mu = m$(x軸が$m$)の確率密度が最大になります。よって、$m$が大きくなるほど山が右に移動します。
βの影響
$\beta$の値を変化させ、$m, a, b$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータとして利用する値を作成 beta_vals <- seq(from = 0.1, to = 10, by = 0.1) # 固定するパラメータを指定 m <- 0 a <- 5 b <- 6 # パラメータごとにガウス-ガンマ分布を計算 anime_dens_df <- tidyr:::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals, # 確率変数λ beta = beta_vals # パラメータβ ) |> # 全ての組み合わせを作成 dplyr::arrange(beta, mu, lambda) |> # パラメータごとに並べ替え dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens, # 確率密度 parameter = paste0("m=", m, ", beta=", round(beta, 1), ", a=", a, ", b=", b) |> factor(levels = paste0("m=", m, ", beta=", round(beta_vals, 1), ", a=", a, ", b=", b)) # フレーム切替用ラベル ) anime_dens_df
## # A tibble: 4,040,100 × 7 ## mu lambda beta N_dens Gam_dens density parameter ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -3 0 0.1 0 0 0 m=0, beta=0.1, a=5, b=6 ## 2 -3 0.01 0.1 0.0126 0.00000305 0.0000000383 m=0, beta=0.1, a=5, b=6 ## 3 -3 0.02 0.1 0.0177 0.0000460 0.000000813 m=0, beta=0.1, a=5, b=6 ## 4 -3 0.03 0.1 0.0216 0.000219 0.00000473 m=0, beta=0.1, a=5, b=6 ## 5 -3 0.04 0.1 0.0248 0.000652 0.0000162 m=0, beta=0.1, a=5, b=6 ## 6 -3 0.05 0.1 0.0276 0.00150 0.0000414 m=0, beta=0.1, a=5, b=6 ## 7 -3 0.06 0.1 0.0301 0.00293 0.0000881 m=0, beta=0.1, a=5, b=6 ## 8 -3 0.07 0.1 0.0323 0.00511 0.000165 m=0, beta=0.1, a=5, b=6 ## 9 -3 0.08 0.1 0.0344 0.00821 0.000283 m=0, beta=0.1, a=5, b=6 ## 10 -3 0.09 0.1 0.0363 0.0124 0.000450 m=0, beta=0.1, a=5, b=6 ## # … with 4,040,090 more rows
mu_vals・lambda_vals・beta_valsの全ての組み合わせを作成して、同様に処理します。
「mの影響」のコードで作図できます。フレーム数はbeta_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(beta_vals), fps = 10, width = 800, height = 600)


$\mu$の分散が$\frac{1}{\beta \lambda}$(精度が$\beta \lambda$)なので、$\beta$が大きくなるほど分散が小さくなり(精度が大きくなり)、x軸($\mu$軸)についての期待値($\mu = m$)付近の確率密度が大きくなります。よって、$\beta$が大きくなるほどx軸に関して細く高い山になります。
aの影響
$a$の値を変化させ、$m, \beta, b$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータとして利用する値を作成 a_vals <- seq(from = 0.1, to = 10, by = 0.1) # 固定するパラメータを指定 m <- 0 beta <- 2 b <- 6 # パラメータごとにガウス-ガンマ分布を計算 anime_dens_df <- tidyr:::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals, # 確率変数λ a = a_vals # パラメータa ) |> # 全ての組み合わせを作成 dplyr::arrange(a, mu, lambda) |> # パラメータごとに並べ替え dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens, # 確率密度 parameter = paste0("m=", m, ", beta=", beta, ", a=", round(a, 1), ", b=", b) |> factor(levels = paste0("m=", m, ", beta=", beta, ", a=", round(a_vals, 1), ", b=", b)) # フレーム切替用ラベル ) anime_dens_df
## # A tibble: 4,040,100 × 7 ## mu lambda a N_dens Gam_dens density parameter ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -3 0 0.1 0 Inf NaN m=0, beta=2, a=0.1, b=6 ## 2 -3 0.01 0.1 0.0516 7.47 0.385 m=0, beta=2, a=0.1, b=6 ## 3 -3 0.02 0.1 0.0666 3.77 0.251 m=0, beta=2, a=0.1, b=6 ## 4 -3 0.03 0.1 0.0746 2.47 0.184 m=0, beta=2, a=0.1, b=6 ## 5 -3 0.04 0.1 0.0787 1.79 0.141 m=0, beta=2, a=0.1, b=6 ## 6 -3 0.05 0.1 0.0804 1.38 0.111 m=0, beta=2, a=0.1, b=6 ## 7 -3 0.06 0.1 0.0805 1.10 0.0889 m=0, beta=2, a=0.1, b=6 ## 8 -3 0.07 0.1 0.0795 0.905 0.0719 m=0, beta=2, a=0.1, b=6 ## 9 -3 0.08 0.1 0.0777 0.755 0.0587 m=0, beta=2, a=0.1, b=6 ## 10 -3 0.09 0.1 0.0753 0.640 0.0482 m=0, beta=2, a=0.1, b=6 ## # … with 4,040,090 more rows
mu_vals・lambda_vals・a_valsの全ての組み合わせを作成して、同様に処理します。
「mの影響」のコードで作図できます。フレーム数はa_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(a_vals), fps = 10, width = 800, height = 600)


$\lambda$(ガンマ分布)の最頻値が$\frac{a - 1}{b}$なので、$\lambda = \frac{a - 1}{b}$(y軸が$\frac{a - 1}{b}$)の確率密度が最大になります。よって、$a$が大きくなるほど山が上に移動します。
また、$\lambda$は$\mu$(ガウス分布)の精度に比例するので、$\lambda$(y軸)が大きくなるほど、$\mu$(x軸)の分散が小さくなり(精度が大きくなり)、山が細く高くなります。
bの影響
$b$の値を変化させ、$m, \beta, a$を固定して、それぞれ分布を計算します。
・作図コード(クリックで展開)
# パラメータとして利用する値を作成 b_vals <- seq(from = 0.1, to = 10, by = 0.1) # 固定するパラメータを指定 m <- 0 beta <- 2 a <- 5 # パラメータごとにガウス-ガンマ分布を計算 anime_dens_df <- tidyr:::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals, # 確率変数λ b = b_vals # パラメータb ) |> # 全ての組み合わせを作成 dplyr::arrange(b, mu, lambda) |> # パラメータごとに並べ替え dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens, # 確率密度 parameter = paste0("m=", m, ", beta=", beta, ", a=", a, ", b=", round(b, 1)) |> factor(levels = paste0("m=", m, ", beta=", beta, ", a=", a, ", b=", round(b_vals, 1))) # フレーム切替用ラベル ) anime_dens_df
## # A tibble: 4,040,100 × 7 ## mu lambda b N_dens Gam_dens density parameter ## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct> ## 1 -3 0 0.1 0 0 0 m=0, beta=2, a=5, b=0.1 ## 2 -3 0.01 0.1 0.0516 4.16e-15 2.15e-16 m=0, beta=2, a=5, b=0.1 ## 3 -3 0.02 0.1 0.0666 6.65e-14 4.43e-15 m=0, beta=2, a=5, b=0.1 ## 4 -3 0.03 0.1 0.0746 3.36e-13 2.51e-14 m=0, beta=2, a=5, b=0.1 ## 5 -3 0.04 0.1 0.0787 1.06e-12 8.36e-14 m=0, beta=2, a=5, b=0.1 ## 6 -3 0.05 0.1 0.0804 2.59e-12 2.08e-13 m=0, beta=2, a=5, b=0.1 ## 7 -3 0.06 0.1 0.0805 5.37e-12 4.32e-13 m=0, beta=2, a=5, b=0.1 ## 8 -3 0.07 0.1 0.0795 9.93e-12 7.90e-13 m=0, beta=2, a=5, b=0.1 ## 9 -3 0.08 0.1 0.0777 1.69e-11 1.32e-12 m=0, beta=2, a=5, b=0.1 ## 10 -3 0.09 0.1 0.0753 2.71e-11 2.04e-12 m=0, beta=2, a=5, b=0.1 ## # … with 4,040,090 more rows
mu_vals・lambda_vals・b_valsの全ての組み合わせを作成して、同様に処理します。
「mの影響」のコードで作図できます。フレーム数はb_valsの要素数です。
# gif画像を作成 gganimate::animate(anime_dens_graph, nframes = length(b_vals), fps = 10, width = 800, height = 600)


$b$が大きくなるほど、$\lambda$の最頻値が小さくなるので、山が下に移動します。
また、$\lambda$(y軸)が小さくなるほど、$\mu$(x軸)の分散が大きくなり(精度が小さくなり)、山が太く低くなります。
この記事では、ガウス-ガンマ分布の作図を確認しました。次は、乱数を生成します。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
書いておきたかった2つ目の分布まで辿り着いた。
2022年2月2日は、モーニング娘。'22の牧野真莉愛さんの21歳のお誕生日です!!
この圧倒的美少女感とキャラのギャップが凄い。
- 2022.08.19:加筆修正しました。
今回はどこまで進められるかな。
【次の内容】