はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、ガウス-ガンマ分布から1次元ガウス分布(一変量正規分布)を生成します。
【前の内容】
【他の記事一覧】
【この記事の内容】
ガウス-ガンマ分布から確率分布の生成
ガウス-ガンマ分布(Gaussian-Gamma Distribution)または正規-ガンマ分布(Normal-Gamma Distribution)から1次元ガウス分布(Gaussian Distribution)を生成します。ガウス分布については「1次元ガウス分布の定義式の確認 - からっぽのしょこ」を参照してください。ガウス-ガンマ分布についてはそのうち書きます。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(patchwork)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
生成分布の設定
まずは、パラメータの生成分布としてガウス-ガンマ分布を設定して、ガウス分布のパラメータを生成(サンプリング)します。
ガウス-ガンマ分布のパラメータ$\mu, \beta, a, b$とサンプルサイズ$N$を設定します。
# ガウス分布の平均パラメータを指定 m <- 0 # ガウス分布の精度パラメータの係数を指定 beta <- 2 # ガンマ分布のパラメータを指定 a <- 5 b <- 6 # 分布の数(サンプルサイズ)を指定 N <- 10
ガウス分布の平均パラメータ$m$と精度パラメータの係数$\beta > 0$、ガンマ分布の形状パラメータ$a > 0$と尺度パラメータ$b > 0$、サンプルサイズ(パラメータ数)$N$を指定します。
ガウス-ガンマ分布に従う乱数を生成します。
# ガンマ分布の精度パラメータを生成 lambda_n <- rgamma(n = N, shape = a, rate = b) # ガウス分布の平均パラメータを生成 mu_n <- rnorm(n = N, mean = m, sd = 1/sqrt(beta*lambda_n)) # パラメータを格納 param_df <- tibble::tibble( mu = mu_n, lambda = lambda_n, parameter = paste0("mu=", round(mu_n, 2), ", lambda=", round(lambda_n, 3)) |> factor() # 色分け用ラベル ) param_df
## # A tibble: 10 × 3 ## mu lambda parameter ## <dbl> <dbl> <fct> ## 1 -1.71 0.412 mu=-1.71, lambda=0.412 ## 2 -0.128 1.98 mu=-0.13, lambda=1.978 ## 3 0.284 1.12 mu=0.28, lambda=1.119 ## 4 -0.248 0.913 mu=-0.25, lambda=0.913 ## 5 0.484 1.15 mu=0.48, lambda=1.146 ## 6 2.23 0.572 mu=2.23, lambda=0.572 ## 7 0.577 1.35 mu=0.58, lambda=1.353 ## 8 0.383 0.517 mu=0.38, lambda=0.517 ## 9 -0.297 0.602 mu=-0.3, lambda=0.602 ## 10 0.738 0.660 mu=0.74, lambda=0.66
先にガンマ分布の乱数を生成して、生成した乱数を精度パラメータ(に比例する値)としてガウス分布の乱数を生成します。
ガンマ分布の乱数は、rgamma()で生成できます。データ数の引数nにN、形状の引数shapeにa、尺度の引数rateにbを指定します。生成した値を精度パラメータ$\lambda$のサンプルlambda_nとします。
ガウス分布の乱数は、rnorm()で生成できます。データ数の引数nにN、平均の引数meanにm、標準偏差の引数sdにbetaとlambda_nの積の平方根の逆数を指定します。生成した値を平均パラメータ$\mu$のサンプルmu_nとします。
ガウス-ガンマ分布の期待値を計算します。
# 平均パラメータの期待値を計算 E_mu <- m # 精度パラメータの期待値を計算 E_lambda <- a / b
$\mu$の期待値$\mathbb{E}[\mu] = m$をE_mu、$\lambda$の期待値$\mathbb{E}[\lambda] = \frac{a}{b}$をE_lambdaとします。
サンプリングされたパラメータとその分布の基準を示すのに使います。
ガウス-ガンマ分布を計算します。
# μの値を作成 mu_vals <- seq( from = E_mu - 1/sqrt(beta*E_lambda) * 4, to = E_mu + 1/sqrt(beta*E_lambda) * 4, length.out = 200 ) # λの値を作成 lambda_vals <- seq(from = 0, to = E_lambda * 3, length.out = 200) # ガウス-ガンマ分布を計算 gaussian_gamma_df <- tidyr::expand_grid( mu = mu_vals, # 確率変数μ lambda = lambda_vals # 確率変数λ ) |> # 確率変数(μとλの格子点)を作成 dplyr::mutate( N_dens = dnorm(x = mu, mean = m, sd = 1/sqrt(beta*lambda)), # μの確率密度 Gam_dens = dgamma(x = lambda, shape = a, rate = b), # λの確率密度 density = N_dens * Gam_dens # 確率密度 ) gaussian_gamma_df
## # A tibble: 40,000 × 5 ## mu lambda N_dens Gam_dens density ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 -3.10 0 0 0 0 ## 2 -3.10 0.0126 0.0561 0.00000748 0.000000420 ## 3 -3.10 0.0251 0.0703 0.000111 0.00000780 ## 4 -3.10 0.0377 0.0763 0.000521 0.0000398 ## 5 -3.10 0.0503 0.0781 0.00153 0.000119 ## 6 -3.10 0.0628 0.0774 0.00346 0.000268 ## 7 -3.10 0.0754 0.0751 0.00665 0.000500 ## 8 -3.10 0.0879 0.0719 0.0114 0.000822 ## 9 -3.10 0.101 0.0682 0.0181 0.00123 ## 10 -3.10 0.113 0.0641 0.0269 0.00172 ## # … with 39,990 more rows
詳しくは「【R】ガウス-ガンマ分布の作図 - からっぽのしょこ」を参照してください。
生成分布(ガウス-ガンマ分布)とパラメータのサンプルをプロットします。
# ガウス-ガンマ分布を作図 gaussian_gamma_graph <- ggplot() + geom_contour_filled(data = gaussian_gamma_df, mapping = aes(x = mu, y = lambda, z = density, fill = ..level..), alpha = 0.6) + # パラメータの生成分布 geom_point(mapping = aes(x = E_mu, y = E_lambda), color = "red", size = 6, shape = 4) + # パラメータの期待値 geom_point(data = param_df, mapping = aes(x = mu, y = lambda, color = parameter), alpha = 0.8, size = 6, show.legend = FALSE) + # パラメータのサンプル labs( title = "Gaussian-Gamma Distribution", subtitle = parse(text = paste0("list(m==", m, ", beta==", beta, ", a==", a, ", b==", b, ")")), fill = "density", x = expression(mu), y = expression(lambda) ) # ラベル gaussian_gamma_graph
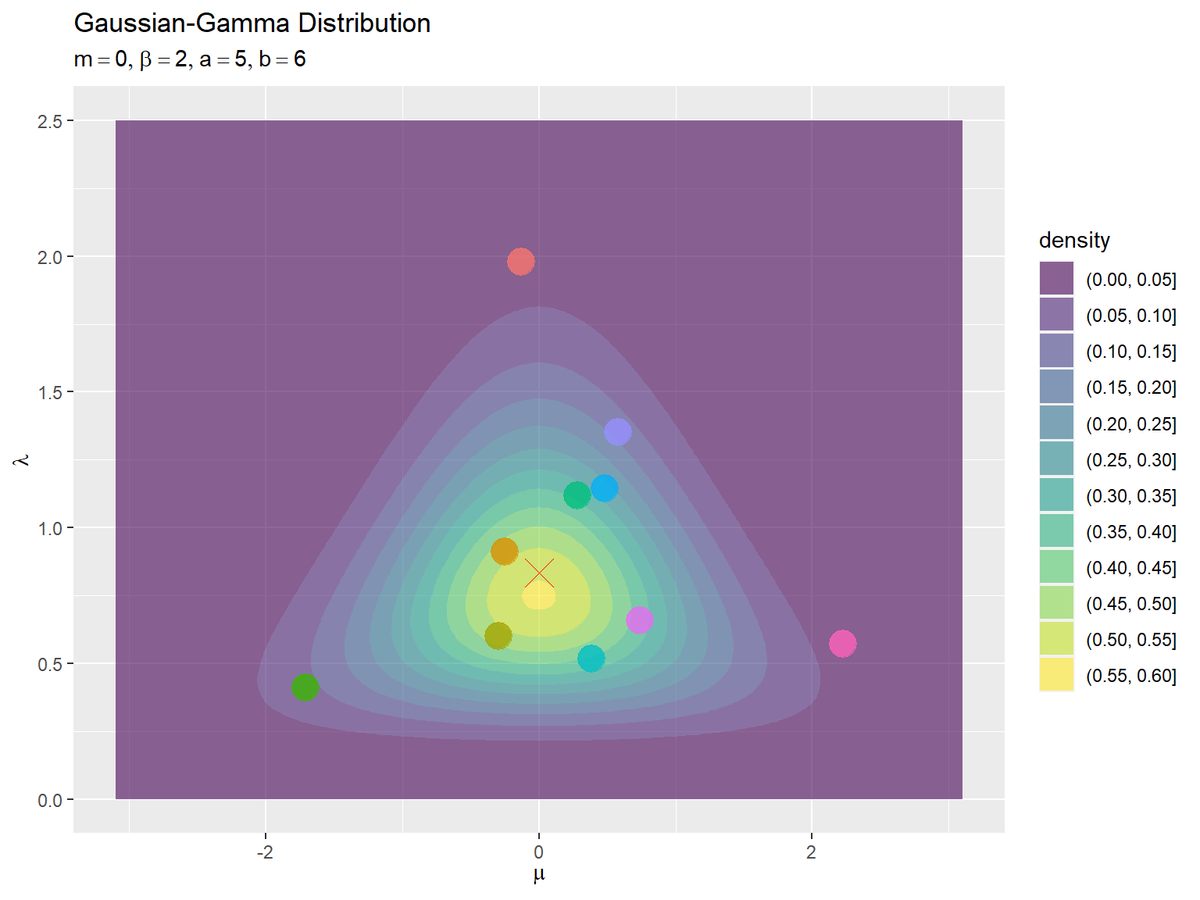
期待値をバツ印で示します。
以上で、生成分布を設定して、パラメータを生成しました。次は、パラメータのサンプルを用いて、ガウス分布を作図します。
分布の作図:1次元ガウス分布
生成した値を1次元ガウス分布の平均パラメータと精度パラメータ(分散パラメータの逆数)として利用します。グラフ作成については「【R】1次元ガウス分布の作図 - からっぽのしょこ」を参照してください。
パラメータのサンプルごとにガウス分布を計算します。
# xの値を作成 x_vals <- mu_vals # パラメータのサンプルごとにガウス分布を計算 res_gaussian_df <- tidyr::expand_grid( x = x_vals, # 確率変数 n = 1:N # パラメータ番号 ) |> # 全ての組み合わせを作成 dplyr::arrange(n, x) |> # パラメータのごとに並べ替え dplyr::mutate( mu = mu_n[n], # パラメータμ lambda = lambda_n[n], # パラメータλ density = dnorm(x = x, mean = mu, sd = 1/sqrt(lambda)), # 確率密度 parameter = paste0("mu=", round(mu, 2), ", lambda=", round(lambda, 3)) |> factor() # 色分け用ラベル ) res_gaussian_df
## # A tibble: 2,000 × 6 ## x n mu lambda density parameter ## <dbl> <int> <dbl> <dbl> <dbl> <fct> ## 1 -3.10 1 -1.71 0.412 0.172 mu=-1.71, lambda=0.412 ## 2 -3.07 1 -1.71 0.412 0.175 mu=-1.71, lambda=0.412 ## 3 -3.04 1 -1.71 0.412 0.178 mu=-1.71, lambda=0.412 ## 4 -3.00 1 -1.71 0.412 0.181 mu=-1.71, lambda=0.412 ## 5 -2.97 1 -1.71 0.412 0.184 mu=-1.71, lambda=0.412 ## 6 -2.94 1 -1.71 0.412 0.187 mu=-1.71, lambda=0.412 ## 7 -2.91 1 -1.71 0.412 0.190 mu=-1.71, lambda=0.412 ## 8 -2.88 1 -1.71 0.412 0.193 mu=-1.71, lambda=0.412 ## 9 -2.85 1 -1.71 0.412 0.196 mu=-1.71, lambda=0.412 ## 10 -2.82 1 -1.71 0.412 0.199 mu=-1.71, lambda=0.412 ## # … with 1,990 more rows
ガウス分布(生成された分布)の確率変数がとり得る値$x$を作成してx_valsとします。この例では、作図時に対応関係が分かりやすいように、mu_valsの値を使います。
$x$の値x_valsとパラメータ番号1:Nそれぞれの要素の全ての組み合わせをexpand_grid()で作成して、mu_n, lambda_nから値を取り出し、それぞれ確率密度を計算します。
ガウス分布の確率密度は、dnorm()で計算できます。確率変数の引数xにx_valsの値、平均の引数meanにmu_nの値、標準偏差の引数sdにlambda_nの値の平方根の逆数を指定します。
凡例を数式で表示する場合は、expression()に対応した記法に変換します。
# 凡例用のラベルを作成:(数式表示用) label_vec <- res_gaussian_df[["parameter"]] |> stringr::str_replace_all(pattern = "=", replacement = "==") |> # 等号表示用の記法に変換 (\(.){paste0("list(", ., ")")})() |> # カンマ表示用の記法に変換 unique() |> # 重複を除去 parse(text = _) # expression化 names(label_vec) <- unique(res_gaussian_df[["parameter"]]) # ggplotに指定する文字列に対応する名前付きベクトルに変換 label_vec[1]
## expression(`mu=-1.71, lambda=0.412` = list(mu == -1.71, lambda == ## 0.412))
3行目の処理では、無名関数function()の省略記法\()を使って、(\(引数){引数を使った具体的な処理})()としています。直前のパイプ演算子を%>%にすると、行全体(\(引数){処理})()を{}の中の処理(この例だとpaste0("list(", ., ")"))に置き換えられます(置き換えられるように引数名を.にしています)。
変換後の文字列のベクトルに対してnames()を使って、元の文字列を各要素の名前として設定します。
ガウス-ガンマ分布の期待値(ガウス分布のパラメータの期待値)を用いて、ガウス分布を計算します。
# パラメータの期待値によるガウス分布を計算 E_gaussian_df <- tidyr::tibble( x = x_vals, # 確率変数 density = dnorm(x = x_vals, mean = E_mu, sd = 1/sqrt(E_lambda)) # 確率密度 ) E_gaussian_df
## # A tibble: 200 × 2 ## x density ## <dbl> <dbl> ## 1 -3.10 0.00667 ## 2 -3.07 0.00723 ## 3 -3.04 0.00782 ## 4 -3.00 0.00846 ## 5 -2.97 0.00914 ## 6 -2.94 0.00987 ## 7 -2.91 0.0106 ## 8 -2.88 0.0115 ## 9 -2.85 0.0124 ## 10 -2.82 0.0133 ## # … with 190 more rows
mean引数にE_mu、sd引数にE_lambdaの平方根の逆数を指定します。
$N + 1$個の1次元ガウス分布を作図します。
# サンプルによる1次元ガウス分布を作図 gaussian_graph <- ggplot() + geom_line(data = E_gaussian_df, mapping = aes(x = x, y = density), color = "red", size = 1, linetype = "dashed") + # 期待値による分布 geom_line(data = res_gaussian_df, mapping = aes(x = x, y = density, color = parameter), alpha = 0.8, size = 1) + # サンプルによる分布 scale_color_hue(labels = label_vec) + # 凡例テキスト:(数式表示用) guides(color = guide_legend(override.aes = list(alpha = 1))) + # 凡例の体裁 theme(legend.text.align = 0) + # 図の体裁 labs( title = "Gaussian Distribution", subtitle = parse(text = paste0("list(E(mu)==", round(E_mu, 2), ", E(lambda)==", round(E_lambda, 3), ")")), x = expression(x), y = "density" ) # ラベル gaussian_graph
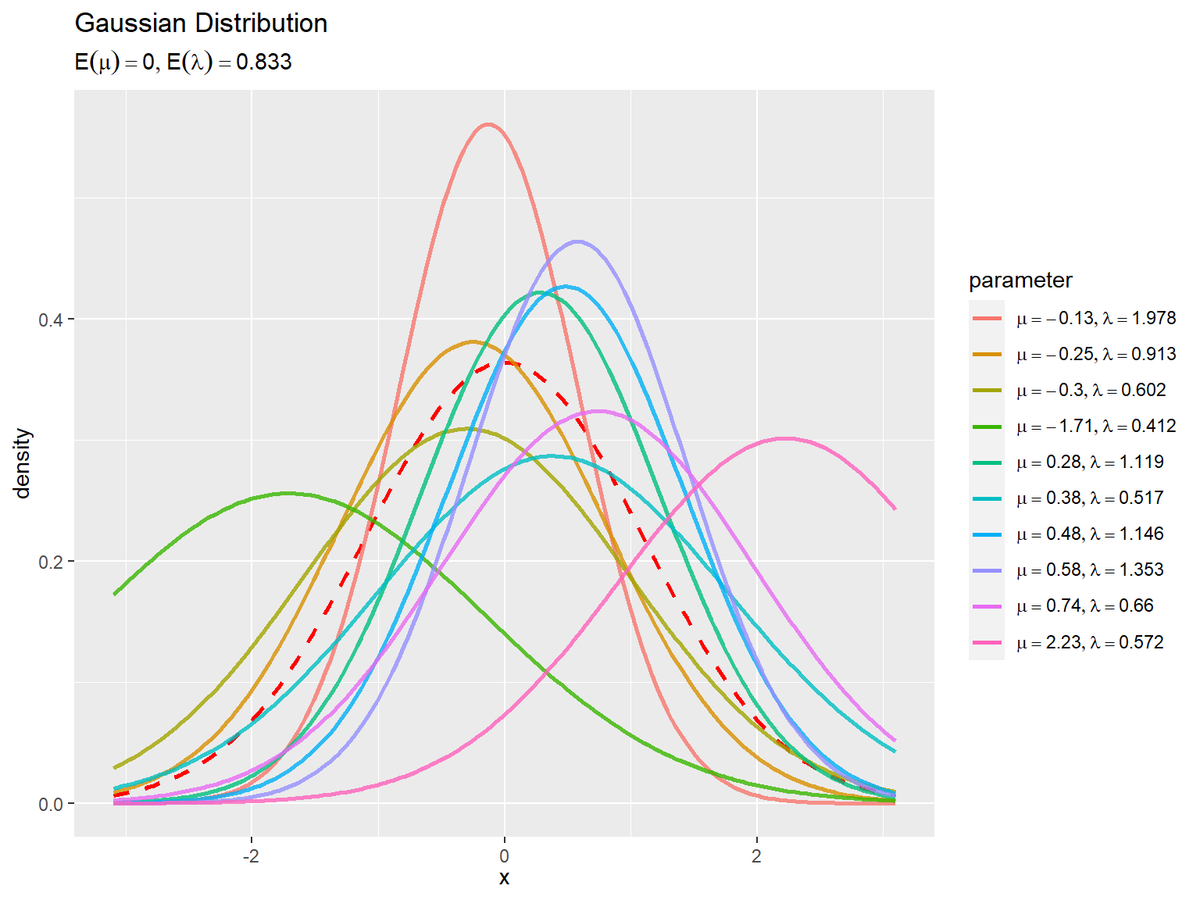
期待値による分布を破線で示します。
パラメータの生成分布(ガウス-ガンマ分布)と生成された分布(ガウス分布)を並べて描画します。
# グラフを並べて描画 gaussian_gamma_graph / gaussian_graph + patchwork::plot_layout(guides = "collect")
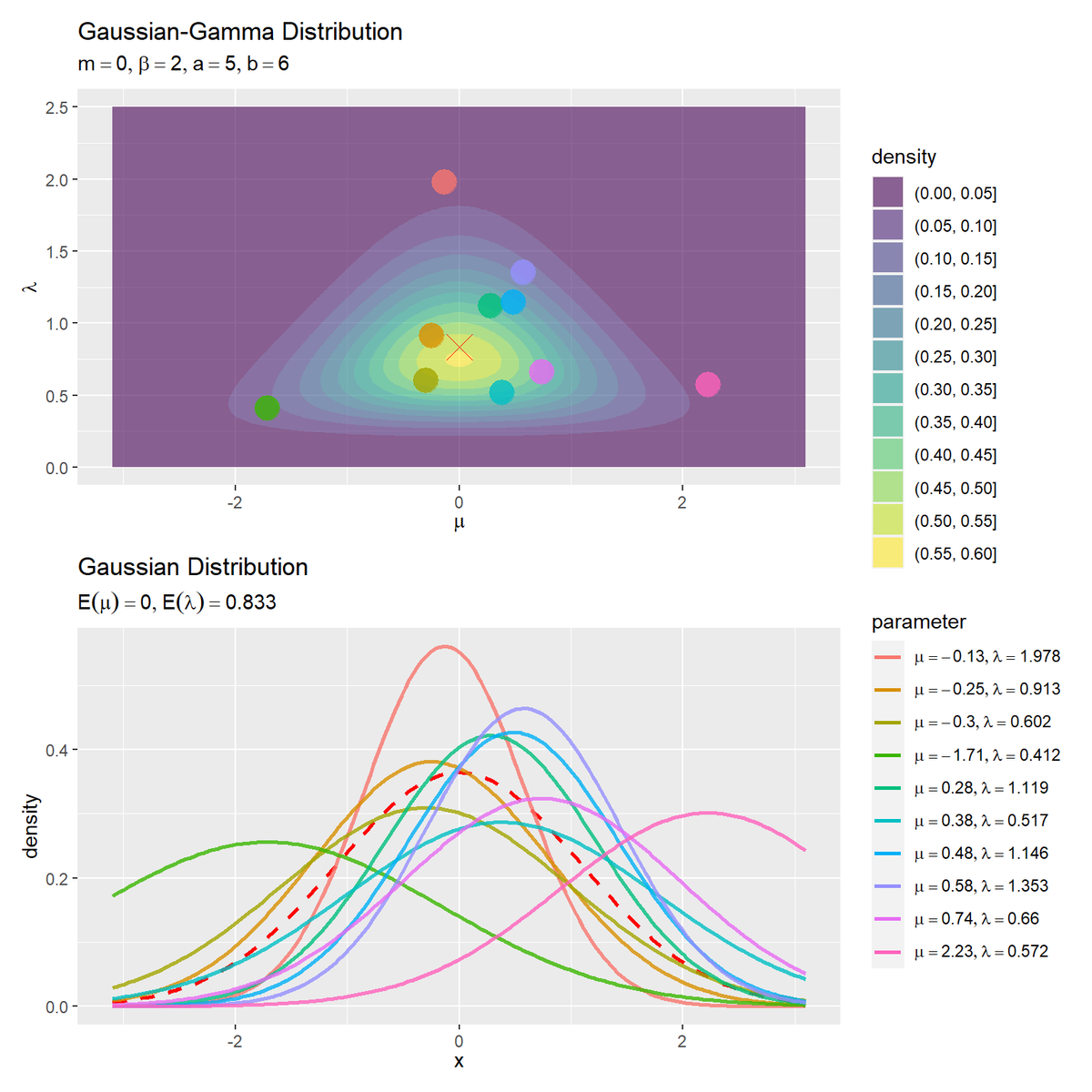
patchworkパッケージの/演算子を使うと上下に並べて描画できます。
平均$\mu$が大きいほど、$x$が大きいほど確率密度が大きくなり、山が右に位置します。また、精度$\lambda$が大きいほど、分散が小さくなるので、平均付近の確率密度が大きくなり、山が高くなります。パラメータのサンプルの点と、分布のピークが対応しているのが分かります。
この記事では、ガウス-ガンマ分布からの分布生成を確認しました。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
加筆修正の際に「ガウス-ガンマ分布の作図」から記事を分割しました。
投稿日に公開されたこの動画をどうぞ。
本当にこの企画最高です。大好き…
【次の内容】