はじめに
『ゼロから作るDeep Learning 3』の初学者向け攻略ノートです。『ゼロつく3』の学習の補助となるように適宜解説を加えていきます。本と一緒に読んでください。
本だけで十分だけど背景などが気になるところをもう少し深堀りして解説していきます。
この記事は、主にステップ46「Optimizerによるパラメータ更新」を補足する内容です。
DeZeroのモジュールとして実装されている各種最適化アルゴリズムを試してみます。
【前ステップの内容】
【他の記事一覧】
【この記事の内容】
・最適化手法の比較
DeZeroのモジュールとして実装されているSGD、Momentum、AdaGrad、AdaDelta、Adamを実際に使ってみましょう。各アルゴリズムについては、「『ゼロから作るDeep Learning』の学習ノート:記事一覧 - からっぽのしょこ」を参照してください(AdaDeltaについては書いていないのでその内書き足します)。
次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import LogNorm from matplotlib.animation import FuncAnimation
グラフの対数スケーリングにcolorsモジュールのLogNorm()を使います。更新値の推移をアニメーション(gif画像)で確認するのにanimationモジュールのFuncAnimation()を使います。
また、これまでに実装済したクラスを利用します。dezeroフォルダの親フォルダまでのパスをsys.path.append()に指定します。
# 実装済みモジュールの読み込み用設定 import sys #sys.path.append('..') sys.path.append('../deep-learning-from-scratch-3-master') # マスターデータ # 利用する実装済みモジュール from dezero import Parameter, Model from dezero import optimizers
・作図の準備
ローゼンブロック関数のグラフ化の詳細は、「ステップ28:ローゼンブロック関数の可視化【ゼロつく3のノート(メモ)】 - からっぽのしょこ」を参照してください。
x軸とy軸の値を作成して、ローゼンブロック関数(z軸の値)を計算します。
# x軸の値を作成 x0_line = np.linspace(-2.0, 2.0, num=500) # y軸の値を作成 x1_line = np.linspace(-1.0, 3.0, num=500) # 格子状の点を作成 x0_grid, x1_grid = np.meshgrid(x0_line, x1_line) # ローゼンブロック関数を計算 y_grid = 100.0 * (x1_grid - x0_grid**2)**2 + (1.0 - x0_grid)**2
等高線を引くz軸の値を作成します。
# log10(y)の最小値を取得 y_log10_min = np.floor(np.log10(y_grid.min()) - 1) # log10(y)の最大値を取得 y_log10_max = np.ceil(np.log10(y_grid.max()) + 1) # log(y)の最小値から最大値までを等間隔に切り分けて間を取り出す lev_log10 = np.linspace(y_log10_min, y_log10_max, num=45)[25:35] # yに対応した値に戻す levs = np.power(10, lev_log10)
作図します。
# 等高線図を作成 plt.figure(figsize=(12, 9)) plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # 最小値 plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.xlabel('$x_0$', fontsize=15) # x軸ラベル plt.ylabel('$x_1$', fontsize=15) # y軸ラベル plt.title('Rosenbrock Function', fontsize=20) # タイトル plt.colorbar(label='y') # 等高線の値 plt.show()

青の星マークが最小値を示しています。
・勾配降下法による探索
各種最適化アルゴリズムを用いてローゼンブロック関数の最小値を探索します。
Modelクラスを継承してローゼンブロック関数(28.1)を作成します。
# ローゼンブロッククラスを定義 class Rosenbrock(Model): # 初期化メソッド def __init__(self, x0, x1): # 初期化メソッドに処理を追加 super().__init__() # パラメータとして値を保存 self.x0 = Parameter(np.array([x0])) self.x1 = Parameter(np.array([x1])) # 順伝播メソッド def forward(self): # 値を取得 x0, x1 = self.x0, self.x1 # ローゼンブロック関数を計算 y = 100 * (x1 - x0**2)**2 + (1 - x0)**2 return y
(たぶんこんな感じです。)
繰り返し試行の終了条件を設定します。点$(x_0, x_1)$と真の値$(1, 1)$との距離$\sqrt{(1 - x_0)^2 + (1 - x_1)^2}$が、thresholdに指定した値よりも近付く(小さくなる)と終了します。または、max_iterに指定した回数に達しても終了します。
点$(x_0, x_1)$の初期値をスカラで指定します。また、更新値の推移を確認するために、値を更新するごとにリストtrace_xに格納していきます。
学習係数を指定して、最適化手法のインスタンスを作成します。他のハイパーパラメータについてはデフォルト値を使っています。(AdaDeltaに関しては学習係数ではないですが処理の都合上学習係数のオブジェクトをそのまま使っています。)
# 終了条件(最大試行回数と閾値)を指定 max_iter = 5000 threshold = 0.05 # 初期値を指定 x0 = 0.0 x1 = 2.0 # モデルのインスタンスを作成 model = Rosenbrock(x0, x1) # 学習学習を指定 lr = 0.5 # 最適化手法のインスタンスを作成 #optimizer = optimizers.SGD(lr) #optimizer = optimizers.MomentumSGD(lr) #optimizer = optimizers.AdaDelta(lr) #optimizer = optimizers.AdaGrad(lr) optimizer = optimizers.Adam(lr) optimizer.setup(model) # 更新値の記録用のリストを初期化 trace_x0 = [x0] trace_x1 = [x1] # 最小値を探索 for i in range(max_iter): # ローゼンブロック関数を計算 y = model() # 勾配を初期化 model.cleargrads() # 勾配を計算 y.backward() # 値を更新 optimizer.update() # 更新値を記録 trace_x0.append(model.x0.data.item()) trace_x1.append(model.x1.data.item()) # 指定した距離まで近付くと終了 dist = np.sqrt((1.0 - trace_x0[-1])**2 + (1.0 - trace_x1[-1])**2) if dist < threshold: print('---------- fin ----------') print('iter:' + str(i + 1) + ', dist:' + str(np.round(dist, 3)) + ', x=(' + str(np.round(trace_x0[-1], 3)) + ', ' + str(np.round(trace_x1[-1], 3)) + ')') break # 指定した回数ごとに結果を表示 if (i + 1) % 100 == 0: # iが100で割り切れる場合 print('iter:' + str(i + 1) + ', dist:' + str(np.round(dist, 3)) + ', x=(' + str(np.round(trace_x0[-1], 3)) + ', ' + str(np.round(trace_x1[-1], 3)) + ')')
iter:100, dist:1.064, x=(0.373, 0.141)
iter:200, dist:0.512, x=(0.746, 0.556)
iter:300, dist:0.25, x=(0.883, 0.779)
iter:400, dist:0.115, x=(0.948, 0.898)
---------- fin ----------
iter:497, dist:0.05, x=(0.978, 0.955)
ローゼンブロック関数のグラフに点$(x_0, x_1)$の経路を重ねて作図します。
# 最適化手法名を取得 opt_name = optimizer.__class__.__name__ # 等高線図を作成 plt.figure(figsize=(9, 9)) plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # 最小値 plt.plot(trace_x0, trace_x1, c='orange', marker='o', mfc='red', mec='red', #alpha=0.5, label='lr=' + str(lr)) # 更新値の推移 plt.xlabel('$x_0$', fontsize=15) # x軸ラベル plt.ylabel('$x_1$', fontsize=15) # y軸ラベル plt.suptitle(opt_name, fontsize=20) # タイトル plt.title('iter:' + str(i + 1), loc='left') plt.legend() # 凡例 #plt.xlim(-2.0, 2.0) # x軸の表示範囲 #plt.ylim(-1.0, 3.0) # y軸の表示範囲 plt.show()
最適化アルゴリズムのインスタンスoptimizerから最適化手法名(クラス名)を抽出して、グラフタイトルに設定しています。

最後におまけとしてアニメーションにしてみます。
・コード(クリックで展開)
# 画像サイズを指定 fig = plt.figure(figsize=(9, 9)) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の試行のトレースプロットを作成 plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # 最小値 plt.plot(trace_x0[:i+1], trace_x1[:i+1], c='orange', marker='o', mfc='red', mec='red', label='lr=' + str(lr)) # 更新値の推移 plt.xlabel('$x_0$', fontsize=15) # x軸ラベル plt.ylabel('$x_1$', fontsize=15) # y軸ラベル plt.suptitle(opt_name, fontsize=20) # 図全体のタイトル plt.title('iter:' + str(i) + ', x=(' + str(np.round(trace_x0[i], 3)) + ', ' + str(np.round(trace_x1[i], 3)) + ')', loc='left') # タイトル plt.legend() # 凡例 plt.xlim(-2.0, 2.0) # x軸の表示範囲 plt.ylim(-1.0, 3.0) # y軸の表示範囲 # gif画像を作成 trace_anime = FuncAnimation(fig, update, frames=101, interval=100) # gif画像を保存 trace_anime.save('step46_' + opt_name + '.gif')

(初期値を含めて)framesに指定した回分だけアニメーション(gif画像)にします。
・実行結果
アルゴリズムや学習係数等のハイパーパラメータによって経路が異なります。いくつか例を見ていきます。SGDの例は「ステップ28:ローゼンブロック関数の可視化【ゼロつく3のノート(メモ)】 - からっぽのしょこ」で行ったので省略します。
・初期値$(0, 2)$の例


Momentumは過去の勾配も利用するため、坂を下り切った後も余力で登っています。


学習率を小さくすると保存される勾配の情報も小さくなるため、最小値から離れる方向への移動は緩和されていますが、学習幅も小さくなり指定した回数では最小値まで到達できていません。
えっと後は適当に感じ取ってください。眺めてるだけでも楽しいですよ。




・初期値$(0.5, 2)$の例












・初期値$(-1.0, 2.5)$の例






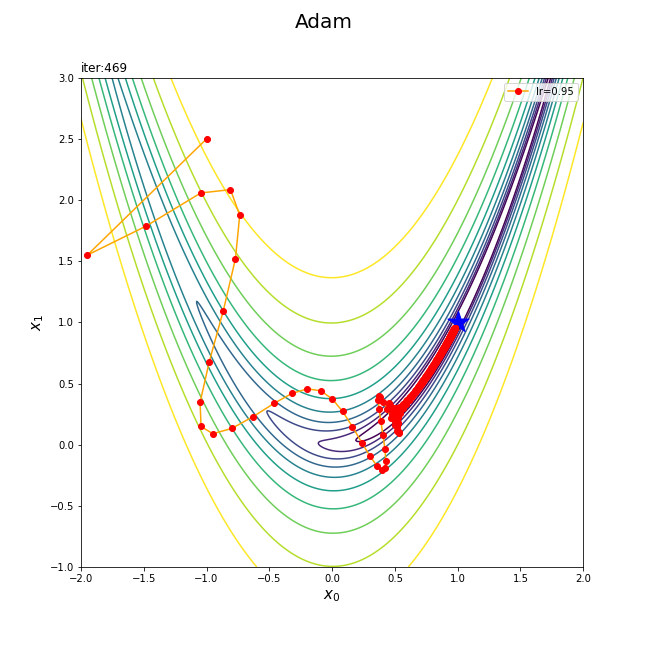

・初期値$(1.5, -0.5)$の例










3Dプロット版や複数手法の比較プロットはこちらの記事で扱いました。
参考文献
おわりに
もはや図の再現ですらないですが、このタイミングで一応やっておきます。こうやって寄り道するのも楽しいよ?あと今回の場合だと図が動いても何も情報が増えてないんですが、動かないより動く方がいいよね(画像ファイルの管理が大変だったけど)。
楽しむだけでなく、どんな問題にどの手法が適しているのかなど色々ちゃんと調べないとなぁ…
【次ステップの内容】
