はじめに
『ゼロから作るDeep Learning 3』の初学者向け攻略ノートです。『ゼロつく3』の学習の補助となるように適宜解説を加えていきます。本と一緒に読んでください。
本だけで十分だけど背景などが気になるところをもう少し深堀りして解説していきます。
この記事は、主にステップ28「関数の最適化」を補足する内容です。
ローゼンブロック関数をグラフ化します。また、ローゼンブロック関数を用いて、勾配降下法をグラフとアニメーションで確認します。
【前ステップの内容】
【他の記事一覧】
【この記事の内容】
・ローゼンブロック関数の可視化
ローゼンブロック関数をmatplotlibを用いて作図します。
ローゼンブロック関数とは、最適化問題のベンチマークとしてよく用いられるテスト関数で、次の式で定義されます。
特に、定数$a = 1, b = 100$が使われます。
作図には次のライブラリを利用します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt #from mpl_toolkits.mplot3d import Axes3D from matplotlib.colors import LogNorm
対数スケーリングにcolorsモジュールのLogNorm()を使います。(手元の環境だとmplot3dモジュールは要らなかったのですが、読み込んでおかないと3Dプロットでエラーになるとかならないとかいうのを見たので、一応メモとして書いておきます。)
・ローゼンブロック関数の計算
まずはローゼンブロック関数の計算を行います。
作図用の点を作成します。
# x軸の値を作成 x0_line = np.linspace(-2.0, 2.0, num=500) print(x0_line[:5]) # y軸の値を作成 x1_line = np.linspace(-1.0, 3.0, num=500) print(x1_line[:5])
[-2. -1.99198397 -1.98396794 -1.9759519 -1.96793587]
[-1. -0.99198397 -0.98396794 -0.9759519 -0.96793587]
$x_0$と$x_1$がとり得る値をnp.linspace()で作成して、それぞれx0_lineとx1_lineとします。第1引数に最小値、第2引数に最大値、引数numに切り分ける要素数を指定します。作図処理が重い場合は、この値を調整してください。
格子状の点を作成します。
# 格子状の点を作成 x0_grid, x1_grid = np.meshgrid(x0_line, x1_line) print(x0_grid[:5, :5]) print(x1_grid[:5, :5]) print(x0_grid.shape)
[[-2. -1.99198397 -1.98396794 -1.9759519 -1.96793587]
[-2. -1.99198397 -1.98396794 -1.9759519 -1.96793587]
[-2. -1.99198397 -1.98396794 -1.9759519 -1.96793587]
[-2. -1.99198397 -1.98396794 -1.9759519 -1.96793587]
[-2. -1.99198397 -1.98396794 -1.9759519 -1.96793587]]
[[-1. -1. -1. -1. -1. ]
[-0.99198397 -0.99198397 -0.99198397 -0.99198397 -0.99198397]
[-0.98396794 -0.98396794 -0.98396794 -0.98396794 -0.98396794]
[-0.9759519 -0.9759519 -0.9759519 -0.9759519 -0.9759519 ]
[-0.96793587 -0.96793587 -0.96793587 -0.96793587 -0.96793587]]
(500, 500)
x軸とy軸の値が直交する点をnp.meshgrid()で作成します。作成したx0_gridはx0_lineを行方向に複製した配列、x1_gridはx1_lineを列方向に複製した配列になります。碁盤の目のように、x0_lineとx1_lineの要素の全ての組み合わせができるように変換されています。
ローゼンブロック関数を計算します。
# 定数を指定 a = 1.0 b = 100.0 # ローゼンブロック関数を計算 y_grid = b * (x1_grid - x0_grid**2)**2 + (a - x0_grid)**2 print(y_grid[:5, :5])
[[2509. 2477.05449576 2445.4407886 2414.15642101 2383.19894533]
[2500.99039361 2469.09619177 2437.53358098 2406.30010372 2375.39331234]
[2492.99363858 2461.15073913 2429.63922471 2398.45663778 2367.6005307 ]
[2485.0097349 2453.21813785 2421.7577198 2390.6260232 2359.82060041]
[2477.03868258 2445.29838793 2413.88906624 2382.80825997 2352.05352148]]
グラフ的にはz軸ですが、本や式に合わせて計算結果をy_gridとしておきます。
次からは、x0_grid, x1_gridとy_gridを使ってグラフを作成していきます。
・3Dプロット
ローゼンブロック関数を3次元のグラフで可視化します。
plot_surface()で3Dのグラフを描画します。
# 3Dプロットを作図 fig = plt.figure(figsize=(12, 9)) # 図の準備 ax = fig.add_subplot(projection='3d') # 3Dプロットの準備 surf = ax.plot_surface(x0_grid, x1_grid, y_grid, cmap='viridis') # 曲面プロット ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('y') # z軸ラベル plt.show()
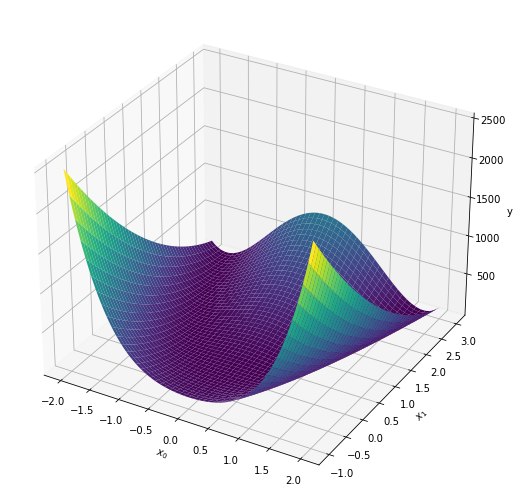
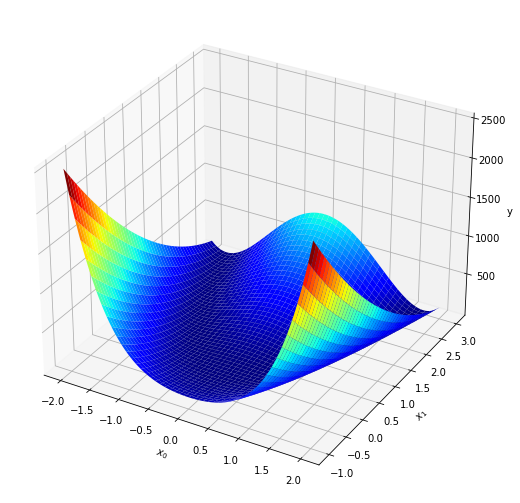
カラーマップの引数cmapでグラフの色を指定できます。左の図は'viridis'、右の図は'jet'です。
ここからは、本の図28-1に寄せていきます。
view_init()でグラフの角度を調整できます。elevに上下方向、azimに左右方向に回転させる角度を指定します。
# 3Dプロットを作図 fig = plt.figure(figsize=(12, 9)) # 図の準備 ax = fig.add_subplot(projection='3d') # 3Dプロットの準備 surf = ax.plot_surface(x0_grid, x1_grid, y_grid, cmap='viridis') # 曲面プロット ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('y') # z軸ラベル ax.view_init(elev=0, azim=0) # 表示アングル plt.show()
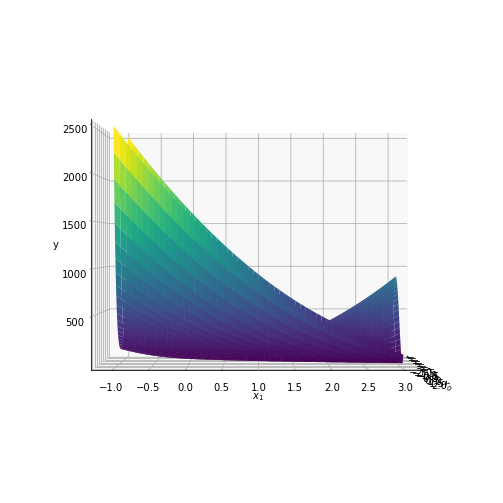
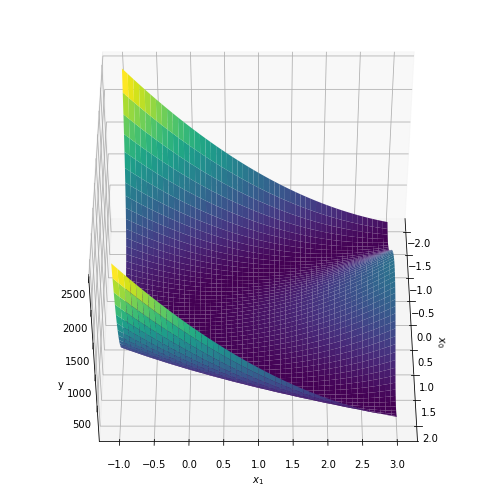
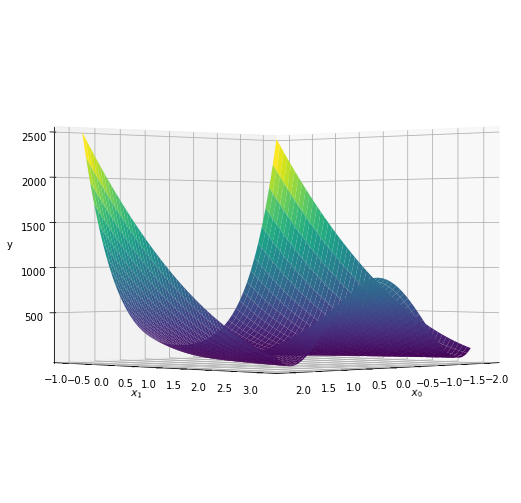
左からelev=0, azim=0、elev=45, azim=0、elev=0, azim=45です。
最適化において注目したいのは関数の最小値です。しかし、$y$の最大値が大きすぎるため、値の小さいところが色分けできていません。
そこで、正規化の引数normで調整します。colorsモジュールのLogNorm()を指定することで対数スケーリングができます。
# 3Dプロットを作図 fig = plt.figure(figsize=(12, 9)) # 図の準備 ax = fig.add_subplot(projection='3d') # 3Dプロットの準備 surf = ax.plot_surface(x0_grid, x1_grid, y_grid, cmap='viridis', norm=LogNorm()) # 曲面プロット ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_zlabel('y') # z軸ラベル ax.set_title('Rosenbrock Function', fontsize=20) # タイトル fig.colorbar(surf, shrink=0.5, aspect=10) ax.view_init(elev=30, azim=240) # 表示アングル plt.show()
colorbar()でカラーバーを付け足せます。引数shrinkには図全体に対するカラーバーの高さの比率、aspectにはカラーバーの横幅に対する高さの比を指定することで、カラーバーのサイズを調整できます。
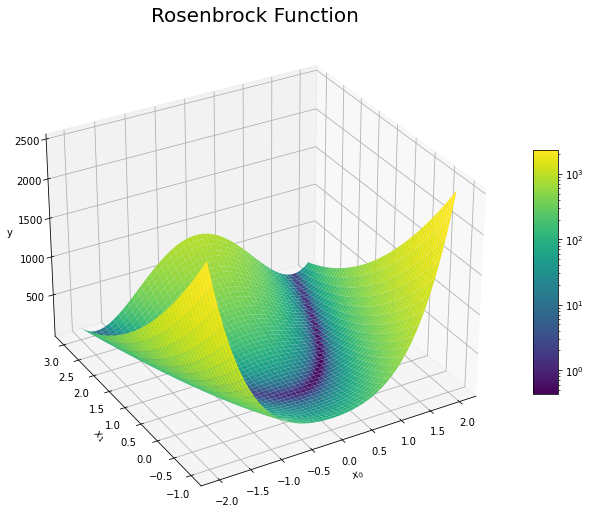
以上で、図28-1を(余分な装飾も足しちゃったけど)概ね再現できました。(表示されている範囲において)急な坂になっている手前側の山と反対側の小山、その間にある放物線状の谷が確認できます。
・2Dプロット
次は、ローゼンブロック関数を2次元のグラフで可視化します。
plt.contour()で等高線を描画します。plt.contourf()を使うと塗りつぶします。
# 等高線図を作図 plt.figure(figsize=(8, 4)) plt.contour(x0_grid, x1_grid, y_grid) # 等高線図 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.colorbar(label='y') # 等高線の値 plt.show()
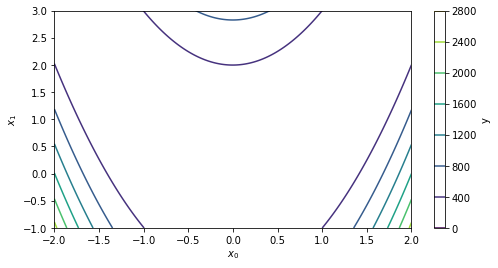
3Dプロットのときと同様に$y$の最大値が大きすぎるため、最小値の辺りが描画されていません。
そこで、先ほどと同様に対数スケーリングします。
# 等高線図を作成 plt.figure(figsize=(8, 4)) plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm()) # 等高線図 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.colorbar(label='y') # 等高線の値 plt.show()

等高線の数が少ない(最小値の付近が何重にもなっている)ので、levels引数に等高線を引く値を指定します。
基本的な方針は、y_gridの最小値から最大値までを等間隔にします。ただし、対数スケールされた状態で等間隔にしたいです。そのため、少し手がかかります。
y_girdの最小値をnp.min()で取り出して、np.log10()で対数化して、そこから更に1を引いた上で、np.floor()で小数点以下を切り捨てた値をy_log10_minとします。同様に、y_girdの最大値をnp.max()で取り出して、np.log10()で対数化して、そこから更に1を足した上で、np.ceil()で小数点以下を切り上げた値をy_log10_maxとします。
y_log10_minを最小値、y_log10_maxを最大値として、np.linspace()で等間隔に分割します。numに指定した値が等高線の数に対応します。
最後に、np.power(10)で10乗することで対数スケールされた値を元に戻します。
# log10(y)の最小値を取得 y_log10_min = np.floor(np.log10(y_grid.min()) - 1) # log10(y)の最大値を取得 y_log10_max = np.ceil(np.log10(y_grid.max()) + 1) # log(y)の最小値から最大値までを等間隔に切り分ける lev_log10 = np.linspace(y_log10_min, y_log10_max, num=25) # yに対応した値に戻す levs = np.power(10, lev_log10) # 確認 print(y_grid.min()) print(y_grid.max()) print(y_log10_min) print(y_log10_max) print(levs)
4.017660992578085e-06
2509.0
-7.0
5.0
[1.00000000e-07 3.16227766e-07 1.00000000e-06 3.16227766e-06
1.00000000e-05 3.16227766e-05 1.00000000e-04 3.16227766e-04
1.00000000e-03 3.16227766e-03 1.00000000e-02 3.16227766e-02
1.00000000e-01 3.16227766e-01 1.00000000e+00 3.16227766e+00
1.00000000e+01 3.16227766e+01 1.00000000e+02 3.16227766e+02
1.00000000e+03 3.16227766e+03 1.00000000e+04 3.16227766e+04
1.00000000e+05]
作成した配列をlevels引数に指定します。
# 等高線図を作成 plt.figure(figsize=(8, 4)) plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs) # 等高線図 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.colorbar(label='y') # 等高線の値 plt.show()

等高線が最小値付近で何重にもなっていて、指定した数の全ては見えていません。最小値付近に線が集まっているのは作成したlevsからも分かります(?)情報としてはこれでいいと思いますが、本の図に寄せておきます。
そこで、先ほどより細かく切り分けて最小値と最大値付近の値(配列の始めと終わりの要素)を間引きます。
# log(y)の最小値から最大値までを等間隔に切り分けて間を取り出す lev_log10 = np.linspace(y_log10_min, y_log10_max, num=45)[25:35] # yに対応した値に戻す levs = np.power(10, lev_log10) print(levs) print(len(levs))
[ 0.65793322 1.23284674 2.3101297 4.32876128 8.11130831 15.19911083 28.48035868 53.36699231 100. 187.38174229] 10
何となくバラついているように感じます(?)
さっきのコードで作図します。
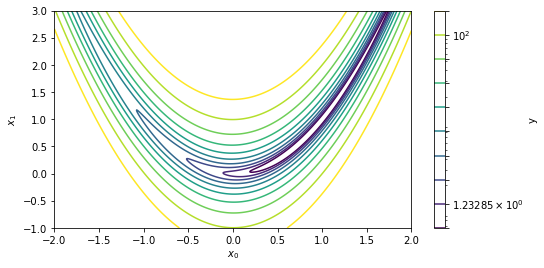
概ね再現できました。この形がバナナに似ていることからバナナ関数と呼ばれます。
最後に、最小値の位置にマークしておきます。
# 等高線図を作成 plt.figure(figsize=(12, 9)) plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # 最小値 plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.title('Rosenbrock Function', fontsize=20) # タイトル #plt.colorbar(label='y') # 等高線の値 plt.show()
zorder引数は、各グラフを重ねる順序を指定する引数です。値が小さいほど背面に配置されます。
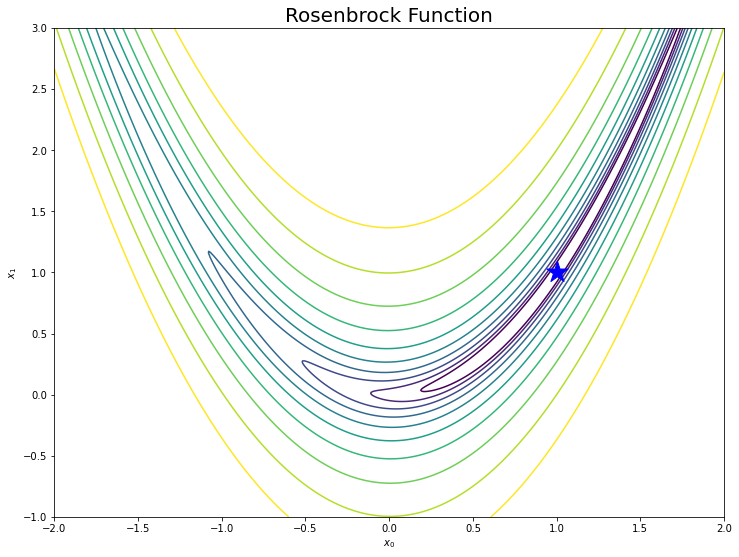
これでローゼンブロック関数の等高線図を描けました。
ちなみに、同じ図を次のコードでも描けます。
# 等高線図を作成 fig = plt.figure(figsize=(12, 9)) # 図の準備 ax = fig.subplots() # グラフの準備 cs = ax.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # 最小値 ax.set_xlabel('$x_0$') # x軸ラベル ax.set_ylabel('$x_1$') # y軸ラベル ax.set_title('Rosenbrock Function', fontsize=20) # タイトル fig.colorbar(cs, label='y') # 等高線の値 plt.show()
以上でローゼンブロック関数の可視化を行えました。次は、ローゼンブロック関数の最小値を勾配降下法を用いて探索します。
・勾配降下法による推移
ローゼンブロック関数に対する勾配降下法を実装します。
勾配降下法による学習には、ここまでで実装したVariableクラスを利用します。第2ステージの最後にdezeroフォルダに実装したVariableクラスを読み込みます。最終的な完成形の(deep-learning-from-scratch-3-masterに実装されている)Variableでは動作しないようです。
# 実装済みのクラスの読み込み用の設定 import sys sys.path.append('..') # Variableクラスの読み込み from dezero import Variable
sys.path.append()で、dezeroフォルダの親フォルダ(親ディレクトリ)をインポート時の検索先ディレクトリに追加します。dezeroフォルダの親フォルダとは、dezeroフォルダが保存されているフォルダのことです。
「現在のnotebookファイルまたはスクリプトファイルが保存されているフォルダ」と「dezeroフォルダ」が同じフォルダに保存されている状態であれば、上の処理で読み込めるはずです。'..'が親ディレクトリを表します。
ファイル構成が異なる場合は、dezeroフォルダまでの絶対パスをsys.path.append()に指定します。Windowsでしたらこんな感じ'C:\\Users\\「ユーザー名」\\Documents\\・・・\\「親フォルダ」'だと思います。
ローゼンブロック関数を作成します。
# ローゼンブロック関数を定義 def rosenbrock(x0, x1): y = 100 * (x1 - x0**2)**2 + (1 - x0)**2 return y
繰り返し計算するので、関数定義しておきます。
勾配降下法により関数の値が小さい方に$(x_0, x_1)$を更新していきます。グラフ化するために更新値をリストに格納していきます。
# 変数を作成(初期値を設定) x0 = Variable(np.array(0.0)) x1 = Variable(np.array(2.0)) # 学習率を指定 lr = 0.001 # 試行回数を指定 iters = 5000 # 更新値の記録用のリストを初期化 x0_list = [x0.data.item()] x1_list = [x1.data.item()] # 勾配降下法 for i in range(iters): # 現在の座標を表示 #print('iter:' + str(i), x0, x1) # 順伝播(ローゼンブロック関数)を計算 y = rosenbrock(x0, x1) # 勾配を初期化 x0.cleargrad() x1.cleargrad() # 逆伝播(勾配)を計算 y.backward() # 勾配降下法による学習 x0.data -= lr * x0.grad x1.data -= lr * x1.grad # 更新値を記録 x0_list.append(x0.data.item()) x1_list.append(x1.data.item())
勾配降下法については、「4.4.1:勾配法【ゼロつく1のノート(数学)】 - からっぽのしょこ」または「6.1.2:SGD【ゼロつく1のノート(実装)】 - からっぽのしょこ」を参照してください。
結果を確認しましょう。5000回繰り返したときの最後の値は次になります。
# 最終結果を確認 print(x0.data.item(), x1.data.item())
0.9569899983530249 0.9156532462021957
真の最小値は$(1, 1)$なので、かなり近くまで辿り着いています。
更新値の経路を等高線図に重ねて可視化します。
# トレースプロットを作成 plt.figure(figsize=(12, 9)) plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # ローゼンブロック関数の最小値 plt.plot(x0_list, x1_list, c='orange', marker='o', mfc='red', mec='red') # 更新値の推移 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.suptitle('Rosenbrock Function : Gradient Descent', fontsize=20) # 図全体のタイトル plt.title('iter:' + str(iters) + ', x=(' + str(np.round(x0.data.item(), 3)) + ', ' + str(np.round(x0.data.item(), 3)) + ')', loc='left') # タイトル plt.show()
plt.plot()の引数c(color)は折れ線の色、markerはマーカーの形状、mfc(markerfacecolor)マーカーの塗りつぶし色、mec(markeredgecolor)はマーカーの枠線の色です。
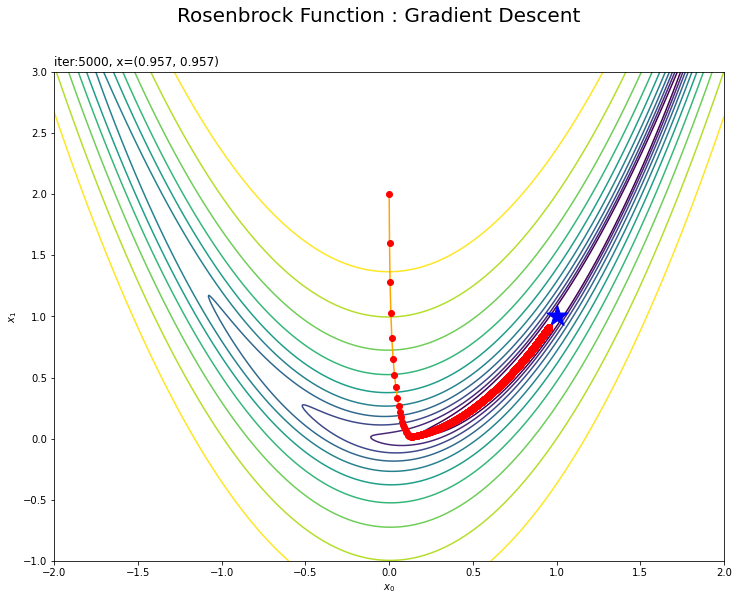
必要な情報の可視化としてはこれでいいと思いますが、まだ少し図28.2とは異なります。折角なのでもう少しこだわってみます。
$(x_0, x_1)$の更新値の点を散布図plt.scatter()でプロットして、その上に重ねて経路を折れ線グラフplt.plot()でプロットいるのだと思います。
# トレースプロットを作成 plt.figure(figsize=(12, 9)) plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # ローゼンブロック関数の最小値 plt.scatter(x0_list, x1_list, marker='o', color='red') # 更新値 plt.plot(x0_list, x1_list, color='orange') # 経路 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.suptitle('Rosenbrock Function : Gradient Descent', fontsize=20) # 図全体のタイトル plt.title('iter:' + str(iters) + ', x=(' + str(np.round(x0.data.item(), 3)) + ', ' + str(np.round(x0.data.item(), 3)) + ')', loc='left') # タイトル plt.show()

以上で、図28-2を(装飾を付け足したけど)概ね再現できました。
おまけとして点$(x_0, x_1)$の推移をアニメーションにしてみます。
・コード(クリックで展開)
# 追加モジュール from matplotlib.animation import FuncAnimation # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i回目の試行のトレースプロットを作成 plt.contour(x0_grid, x1_grid, y_grid, norm=LogNorm(), levels=levs, zorder=0) # ローゼンブロック関数 plt.scatter(1.0, 1.0, marker='*', s=500, c='blue') # ローゼンブロック関数の最小値 plt.plot(x0_list[:i+1], x1_list[:i+1], c='orange', marker='o', mfc='red', mec='red') # 更新値の推移 plt.xlabel('$x_0$') # x軸ラベル plt.ylabel('$x_1$') # y軸ラベル plt.suptitle('Rosenbrock Function : Gradient Descent', fontsize=20) # 図全体のタイトル plt.title('iter:' + str(i) + ', x=(' + str(np.round(x0_list[i], 5)) + ', ' + str(np.round(x1_list[i], 5)) + ')', loc='left') # タイトル # gif画像を作成 trace_anime = FuncAnimation(fig, update, frames=100, interval=100) # gif画像を保存 trace_anime.save('step28_Rosenbrock_GD.gif')
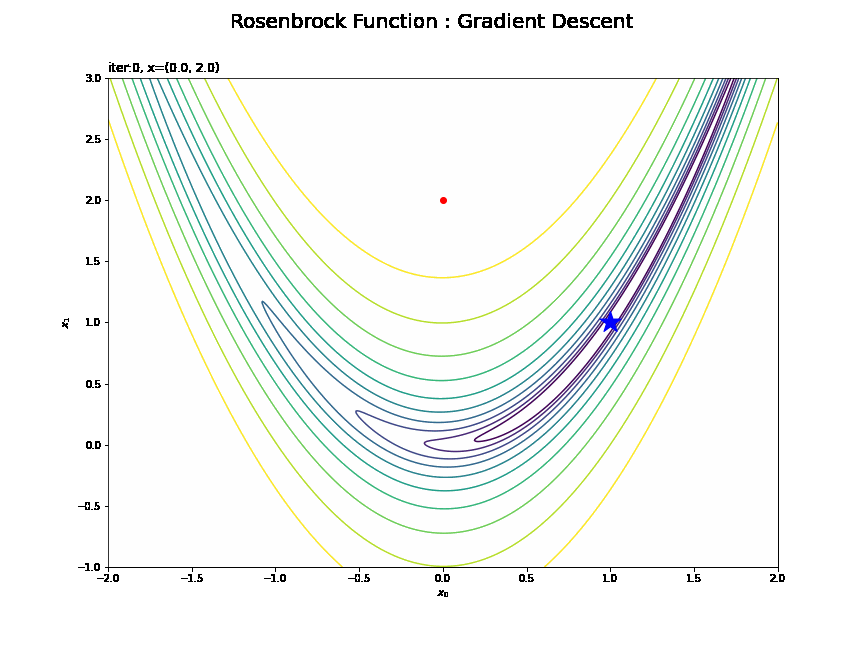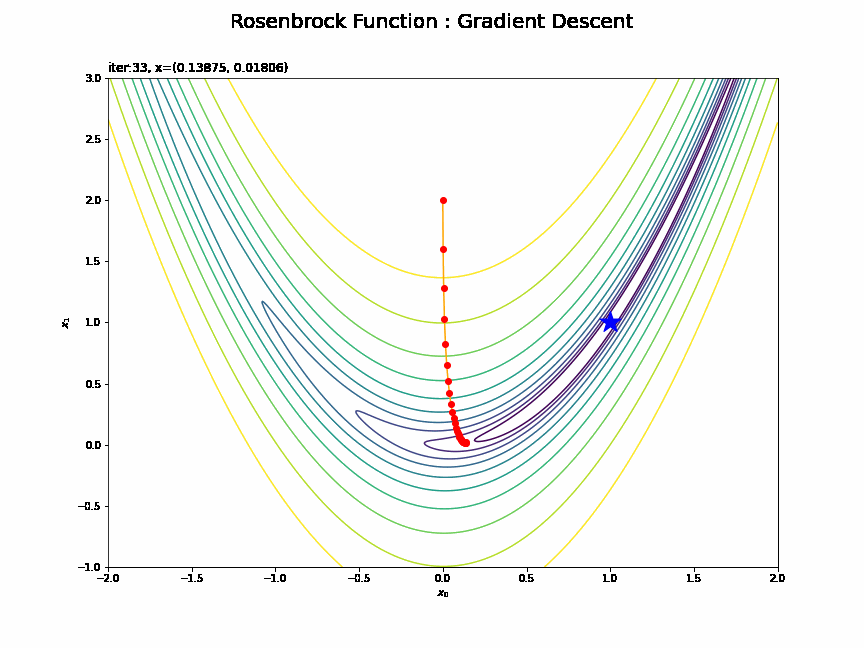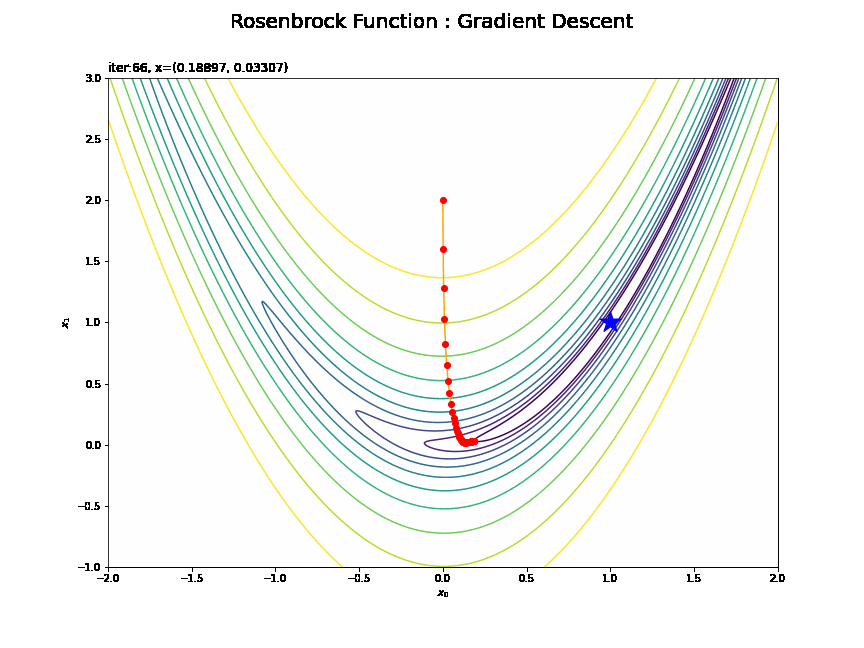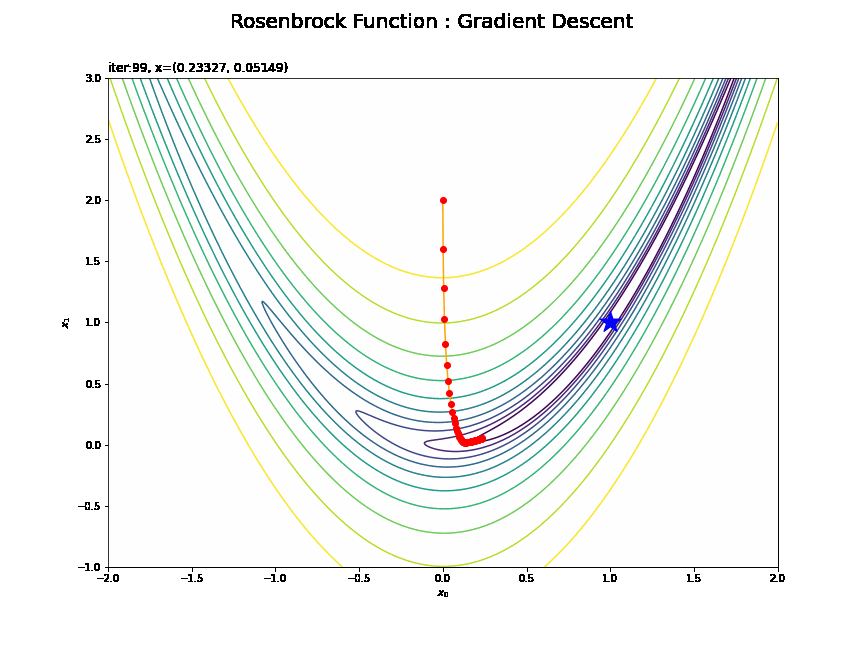
(処理も完成図も)重いので初期値を含めて100回分だけアニメーション(gif画像)にしています。
(3Dプロットと合わせて見ると分かりやすいのですが)山の尾根を下ってから、谷に沿って最小値に向かっているのが分かります。
初期値を変えて試してみましょう。
・$(0.5, 2)$の場合
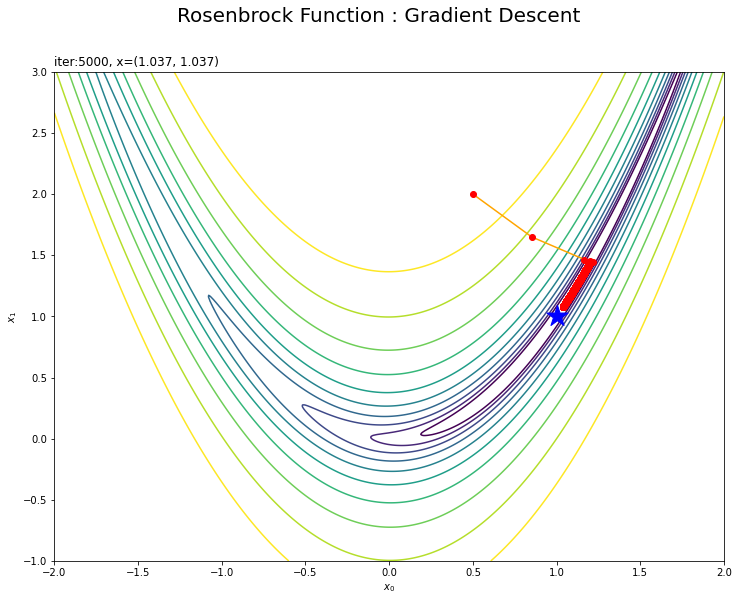
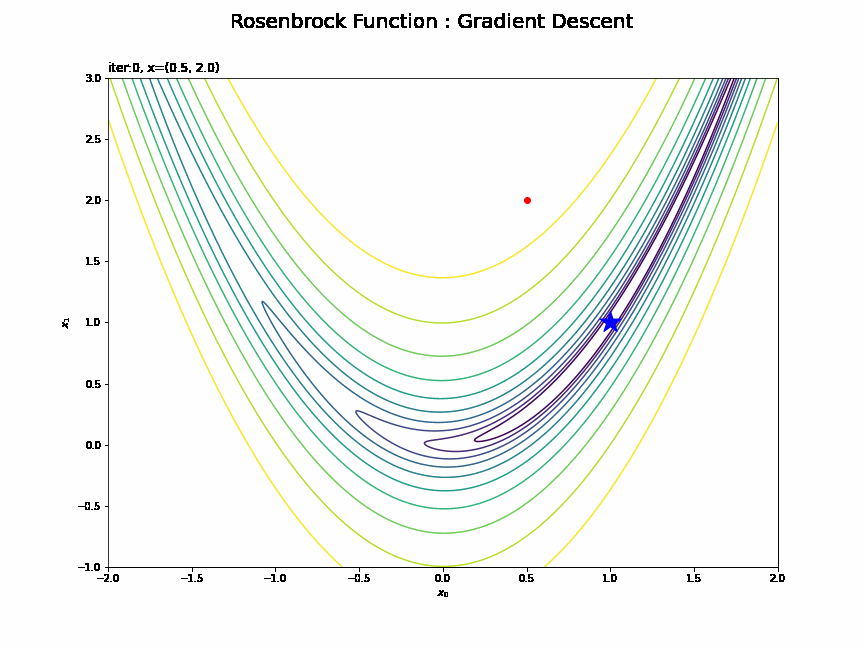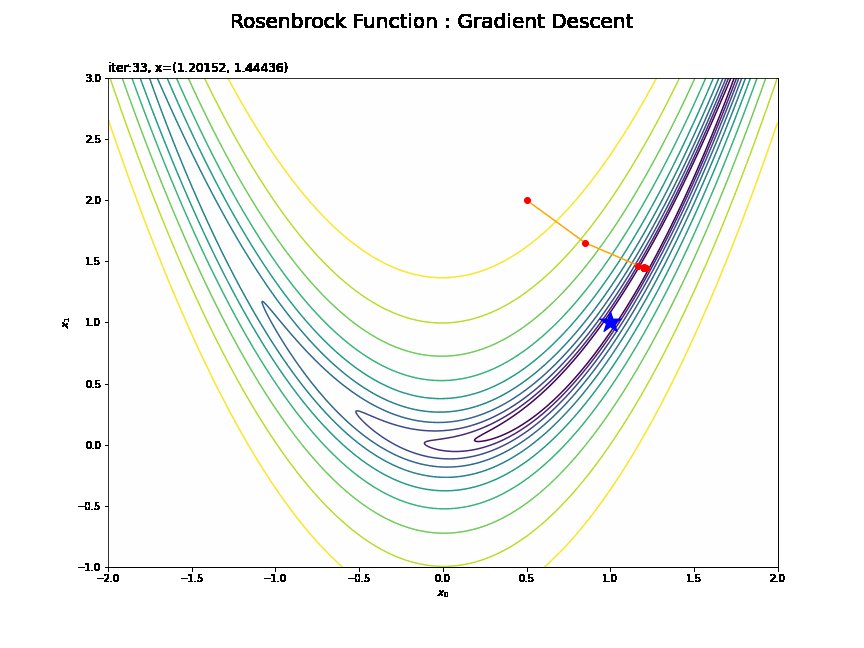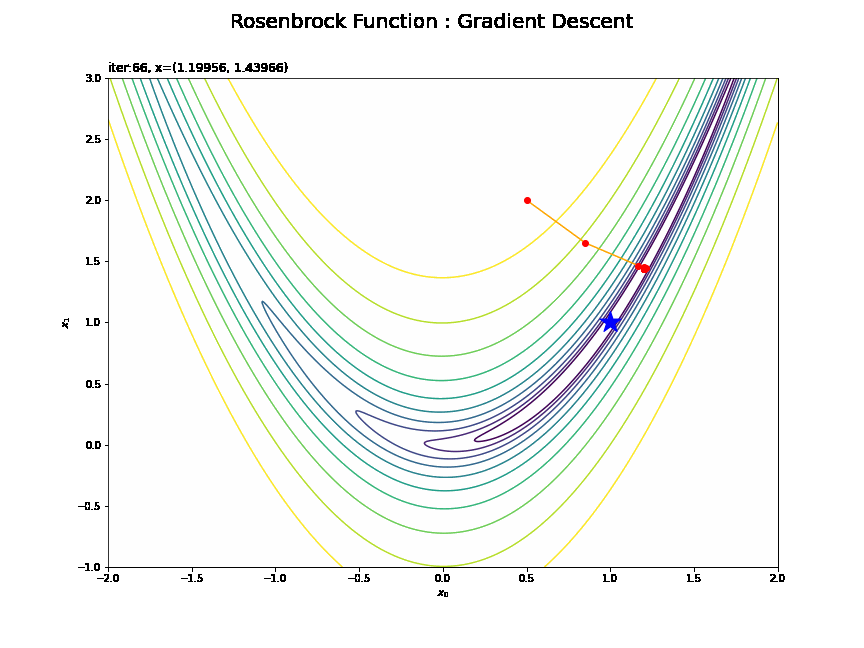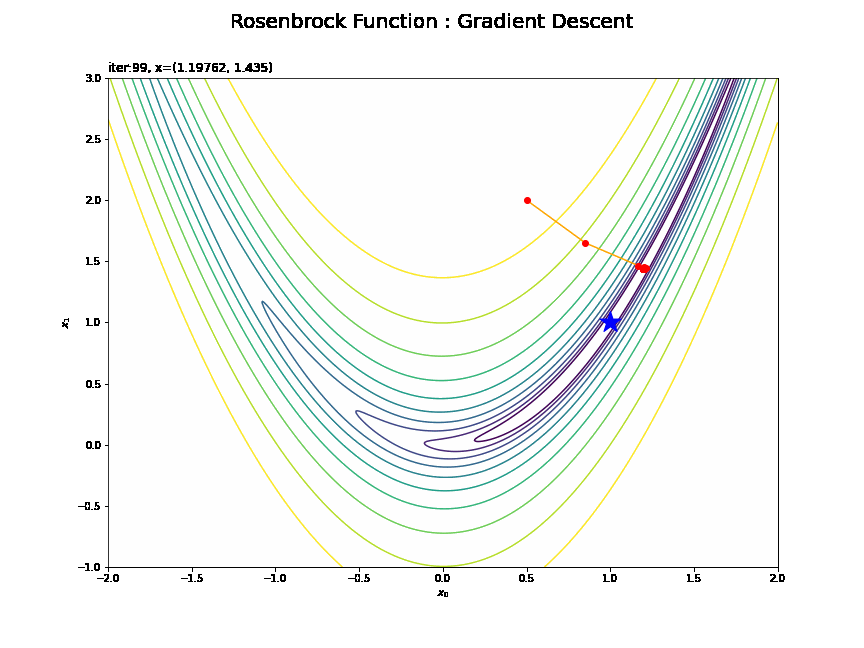
最小値付近は値が更新されにくいのが分かります。勾配が小さい(坂がなだらかだ)と学習幅が小さくなってしまうためです。
・$(-1, 2.5)$の場合
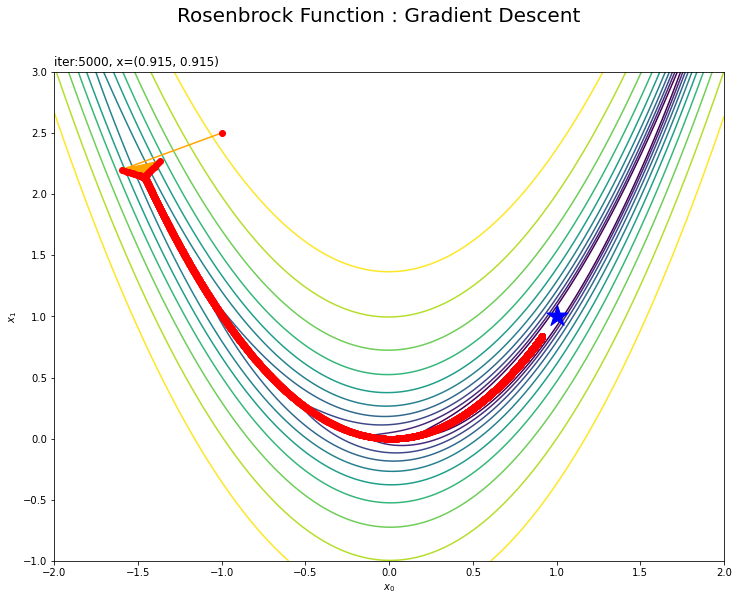
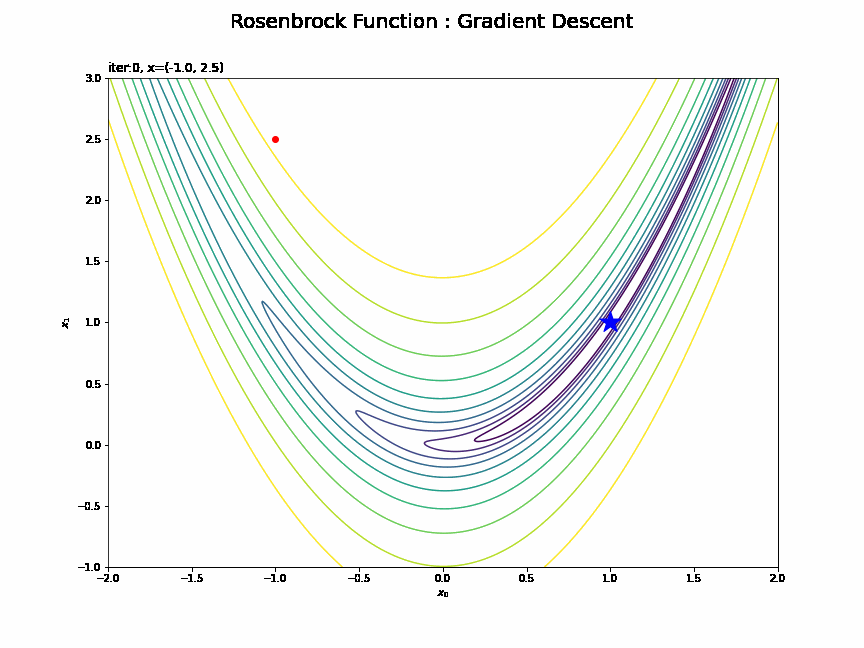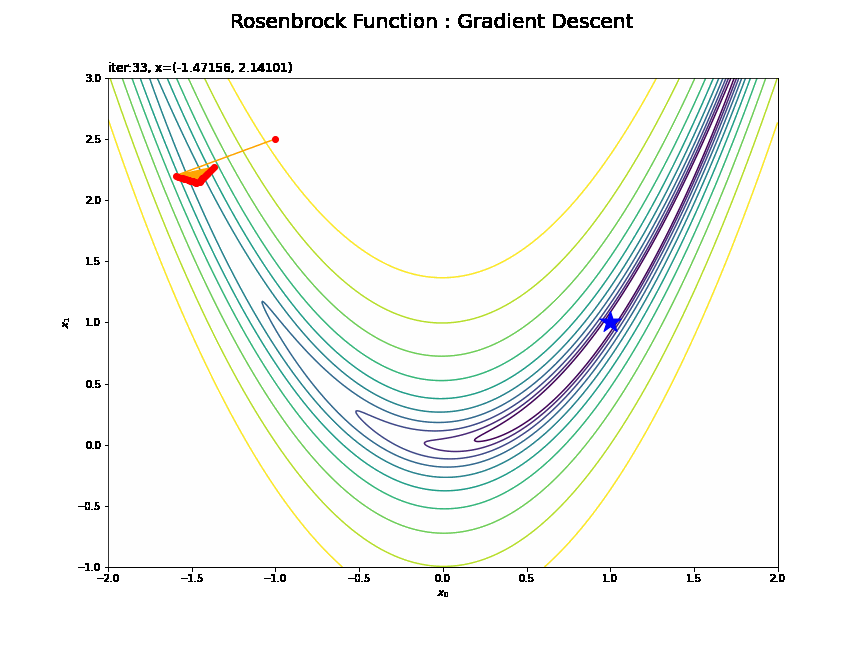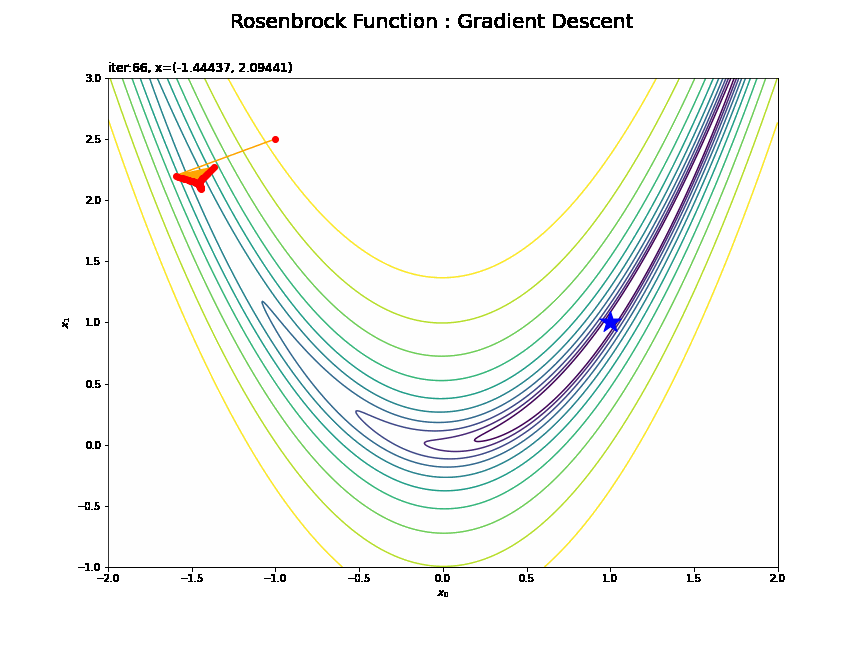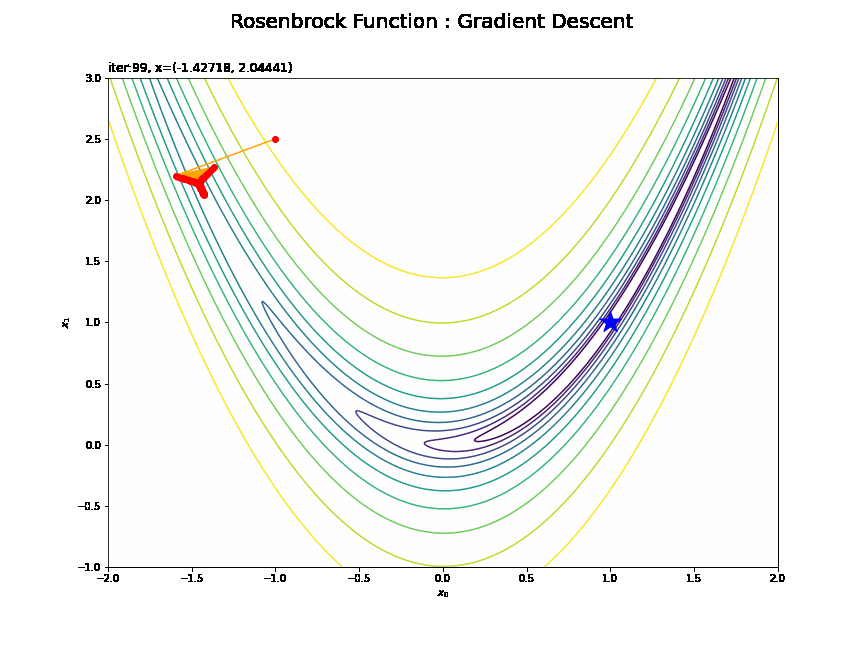
谷の両岸を行ったり来たりしていますね。効率的に探索できているとは言えませんが、最終的には最小値(付近)まで辿り着けています。
・$(1.5, -0.5)$の場合
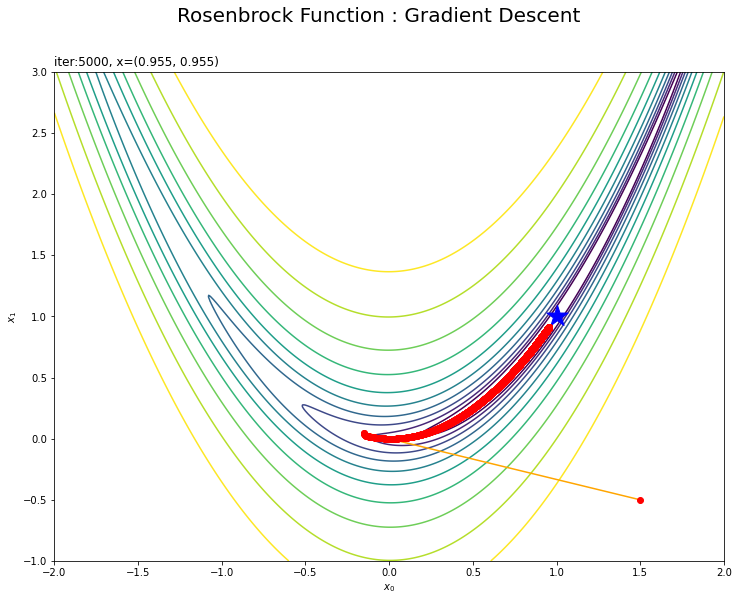
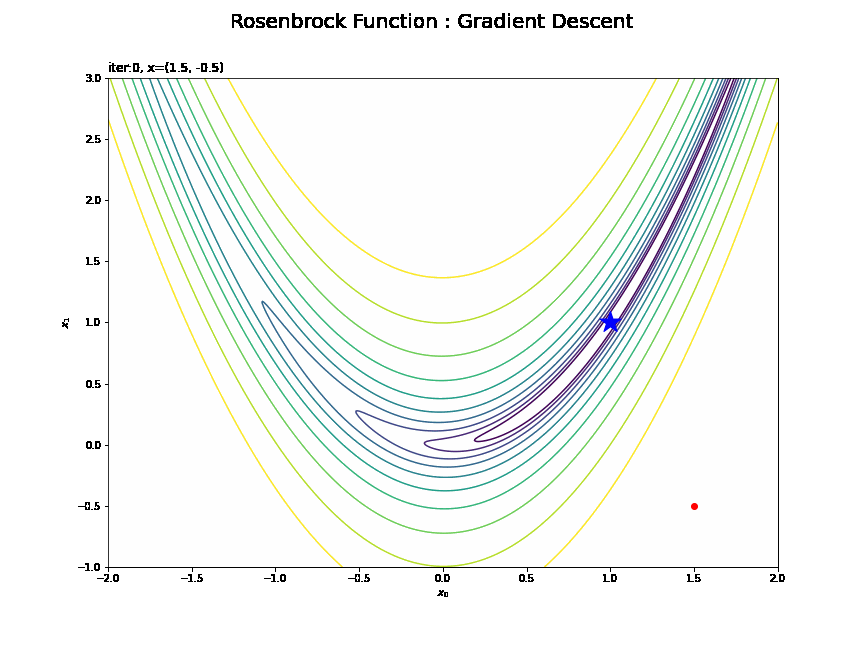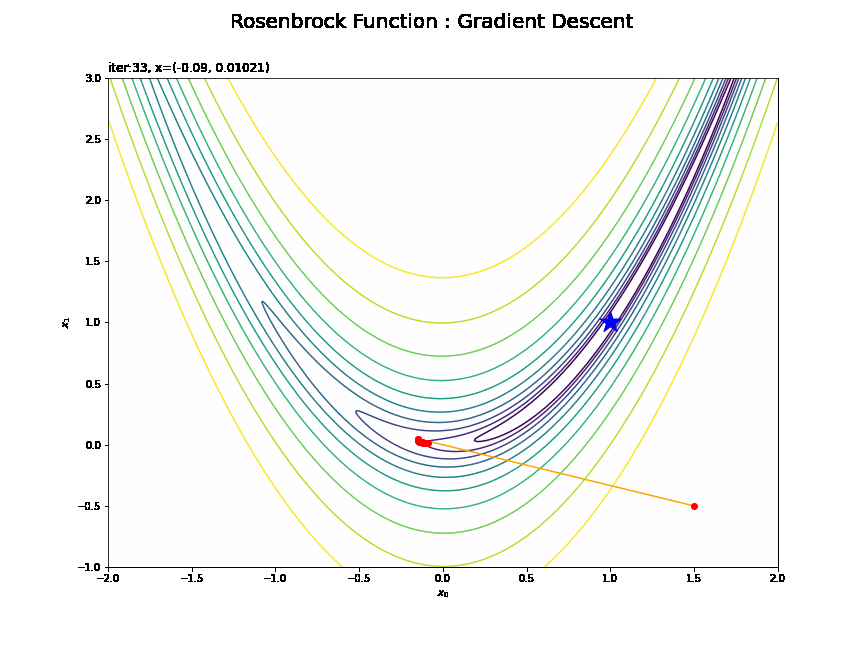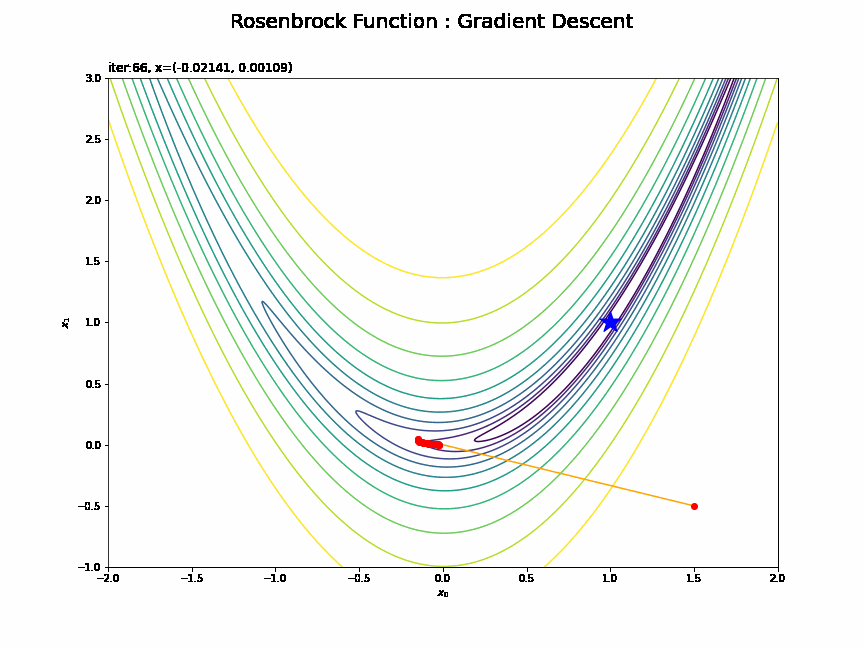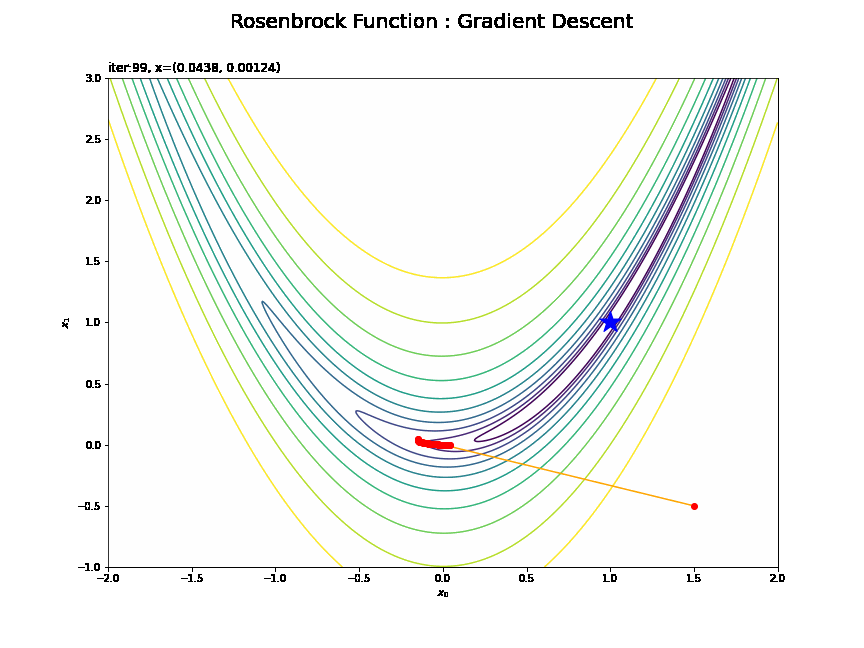
その地点で勾配の大きい(坂が急な)方向に移動するので、最小値から離れるように動くこともあります。
以上で、ローゼンブロック関数に対する勾配降下法の可視化ができました。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 3 ――フレームワーク編』オライリー・ジャパン,2020年.
おわりに
特に何の問題もなくさくっと進むつもりが思いの外てこずってしまった。ので、ブログとして書き残しておきます。
【次ステップの内容】