はじめに
『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本の内容を1つずつ確認しながらゆっくりと組んでいきます。
この記事は、2.3.5項「ベクトル間の類似度」と2.3.6項「類似度のランキングを表示」の内容です。単語の類似度として用いるコサイン類似度を説明して、Pythonで実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
2.3.5 ベクトル間の類似度
この項では、単語(ベクトル)の類似度を測定する関数を実装します。
# この項で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
・コサイン類似度
類似度としてコサイン類似度を用います。コサイン類似度とは、2つのベクトルを$\mathbf{x} = (x_1, x_2, \cdots, x_n)$、$\mathbf{y} = (y_1, y_2, \cdots, y_n)$として、次の式で定義されます。
分子はベクトルの内積であり、分母の$\|\mathbf{x}\|$はL2ノルムと呼び2乗和の平方根です。
また式(2.1)は
と変形できることから、$\mathbf{x},\ \mathbf{y}$をそれぞれのL2ノルムで割ったベクトルの内積でも計算できます。
式のままなので、早速実装しましょう。
# コサイン類似度の実装 def cos_similarity(x, y, eps=1e-8): # コサイン類似度を計算:式(2.1) nx = x / (np.sqrt(np.sum(x**2)) + eps) ny = y / (np.sqrt(np.sum(y**2)) + eps) return np.dot(nx, ny)
eps($\epsilon$)は、0除算とならないための微小な値です。
実装した関数を使って、ベクトルの値とコサイン類似度の値との関係を見ましょう。
2次元のグラフで描画するために、ベクトルの要素数を2とします。1つ目の値がx軸、2つ目の値がy軸に対応します。
# 2つのベクトルを指定 a_vec = np.array([5.0, 5.0]) b_vec = np.array([3.0, 9.0])
plt.quiver()でベクトルを描きます。第1引数から第4引数までは、それぞれ始点の$x,\ y$、終点の$x,\ y$に対応します。始点は原点であるため、どちらも0を指定します。終点には、各ベクトルの0番目と1番目の要素を指定します。その他の引数の詳細は省略します(そのまま指定してください)。
# コサイン類似度を計算 sim_val = cos_similarity(a_vec, b_vec) # 作図 plt.quiver(0, 0, a_vec[0], a_vec[1], angles='xy', scale_units='xy', scale=1, color='c', label='a') # 有効グラフ plt.quiver(0, 0, b_vec[0], b_vec[1], angles='xy', scale_units='xy', scale=1, color='orange', label='b') # 有効グラフ plt.xlim(min(0, a_vec[0], b_vec[0]) - 1, max(0, a_vec[0], b_vec[0]) + 1) plt.ylim(min(0, a_vec[1], b_vec[1]) - 1, max(0, a_vec[1], b_vec[1]) + 1) plt.legend() # 凡例 plt.grid() # 補助線 plt.title('Similarity:' + str(np.round(sim_val, 3)), fontsize=20) plt.show()

この例では要素数を2の$\mathbf{a} = (5, 5)$としました。これは原点から点$(5, 5)$までを結ぶ直線を意味します。そのため$\mathbf{a}$をベクトルと呼びます。また要素数を3の$\mathbf{a} = (5, 6, 7)$とした場合は、原点からx軸方向に5、y軸方向に6、z軸方向に7の点を指します。このように3次元の座標で表されるベクトルとなることから、3次元ベクトルと呼ばれます。それ以上はイメージしにくいですが$n$次元でも同じことです。
他の値でも試してみましょう。
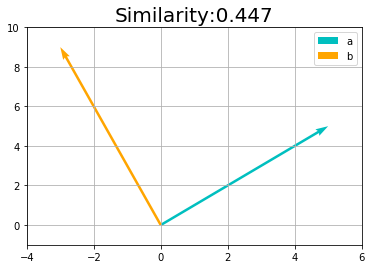
方向の違いとは、2つのベクトルの角度の大きさとも捉えられます。
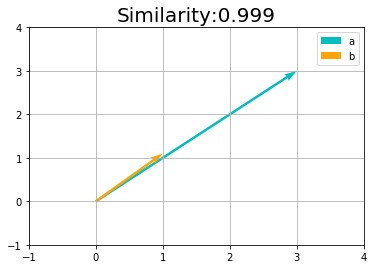
長さ(値の大きさ)に関わりなく、方向が近いとコサイン類似度が高くなります。完全に同じ方向のとき最大値の1となります。
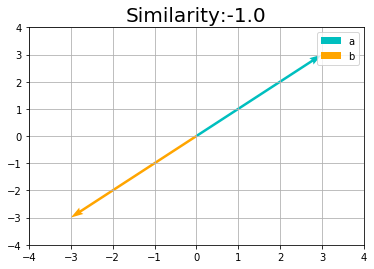
向きが真逆のとき最小値の-1になります。
・単語間の類似度
では前項で作成した各単語ベクトルを用いて、2つの単語の類似度を測りましょう。
比較したい2つの単語を指定して、単語ベクトルからコサイン類似度を計算します。
# テキストを設定 text = 'You say goodbye and I say hello.' # 単語と単語IDに関する変数を取得 corpus, word_to_id, id_to_word = preprocess(text) # 単語の種類数を取得 vocab_size = len(word_to_id) # 共起行列を作成 word_matrix = create_co_matrix(corpus, vocab_size, window_size=1) # 単語を指定して単語ベクトルを取得 c0 = word_matrix[word_to_id['you']] c1 = word_matrix[word_to_id['i']] print(c0) print(c1) # コサイン類似度を計算 sim_val = cos_similarity(c0, c1) print(sim_val)
[0 1 0 0 0 0 0]
[0 1 0 1 0 0 0]
0.7071067691154799
2つの単語間の類似度を計算できました。
次項では、指定した単語と全ての単語との類似度を計算し、類似度の高い単語を見付けます。
2.3.6 類似度のランキングを表示
この項では、指定した単語との類似度が高い単語を表示する(調べる)関数を実装します。
単語を指定して各単語とのコサイン類似度を計算します。対象となる単語をクエリと呼びます。
# 対象とする単語を指定 query = 'you' # 指定した単語のIDを取得 query_id = word_to_id[query] print(query_id) # 指定した単語のベクトルを取得 query_vec = word_matrix[query_id] print(query_vec) # コサイン類似度の記録リストを初期化 vocab_size = len(id_to_word) similarity = np.zeros(vocab_size) # 各単語コサイン類似度を計算 for i in range(vocab_size): similarity[i] = cos_similarity(word_matrix[i], query_vec) # 値を表示 print(list(word_to_id.keys())) print(np.round(similarity, 5))
0
[0 1 0 0 0 0 0]
['you', 'say', 'goodbye', 'and', 'i', 'hello', '.']
[1. 0. 0.70711 0. 0.70711 0.70711 0. ]
最大値の1となった単語がありますが、これは同じ単語なためです。これはランキングから除外する必要があります。
そこでfor文のループ処理中にcontinueを使います。continueが実行されると、それ以降の処理を省略し次の繰り返し処理に移ります。
# continueの使用例 for i in range(5): # 3のときはこれ以上行わない if i == 3: continue print(i)
0
1
2
4
.argsort()メソッドは、配列の要素の値が小さい順にインデックスを返します。しかしここで知りたいのは上位のインデックスです。そこでsimilarityに-1を掛けて符号を反転させることで、大小関係を逆転させます。その出力をfor文に使います。
# 配列を作成 arr = np.array([0, 20, 10, 40, 30]) print(arr) # 低い順のインデックス print(arr.argsort()) # 大小関係を逆転 print(-1 * arr) # 高い順のインデックス print((-1 * arr).argsort())
[ 0 20 10 40 30]
[0 2 1 4 3]
[ 0 -20 -10 -40 -30]
[3 4 1 2 0]
この値は単語IDに対応します。つまりこの出力の0から$n - 1$番目の単語が類似度の上位$n$語になります。
上位$n$語の単語とコサイン類似度を表示する場合、$n + 1$語目からの処理を行う必要がありません。そこでbreakを使います。breakが実行されると、そこでfor文の処理を中断し次の処理に移ります。
# breakの使用例 for i in range(5): # 3以降は行わない if i == 3: break print(i) print('a')
0
1
2
a
これらの機能を組み合わせて、指定した順位までの単語とコサイン類似度を表示します。
# 表示する順位を指定 top = 5 # 類似度上位の単語と値を表示 count = 0 # 表示回数を初期化 for i in (-1 * similarity).argsort(): # 指定した単語のときは次の単語に移る if id_to_word[i] == query: continue # 単語と値を表示 print(' %s: %s' % (id_to_word[i], similarity[i])) # 指定した回数に達したら処理を終了 count += 1 # 表示回数を加算 if count >= top: break
goodbye: 0.7071067691154799
i: 0.7071067691154799
hello: 0.7071067691154799
say: 0.0
and: 0.0
処理の確認ができたので実装しましょう。
# 類似度の上位単語を検索関数の実装 def most_similar(query, word_to_id, id_to_word, word_matrix, top=5): # 指定した単語がテキストに含まれないとき if query not in word_to_id: print('%s is not found' % query) return # 対象の単語を表示 print('\n[query] ' + query) # 指定した単語のIDを取得 query_id = word_to_id[query] # 指定した単語のベクトルを取得 query_vec = word_matrix[query_id] # コサイン類似度を計算 vocab_size = len(id_to_word) similarity = np.zeros(vocab_size) for i in range(vocab_size): similarity[i] = cos_similarity(word_matrix[i], query_vec) # 類似度上位の単語と値を表示 count = 0 # 表示回数を初期化 for i in (-1 * similarity).argsort(): # 指定した単語のときは次の単語に移る if id_to_word[i] == query: continue # 単語と値を表示 print(' %s: %s' % (id_to_word[i], similarity[i])) # 指定した回数に達したら処理を終了 count += 1 # 表示回数を加算 if count >= top: return
実装した関数を試してみましょう。
# クエリを指定 query = 'you' # 類似の単語を表示 most_similar(query, word_to_id, id_to_word, word_matrix, top=5)
[query] you
goodbye: 0.7071067691154799
i: 0.7071067691154799
hello: 0.7071067691154799
say: 0.0
and: 0.0
「say」と別の単語が1というベクトルの構成が同じであるため、3つの単語の値が同じになりました。コーパスのサイズが大きくなる、つまりテキスト中で何度も単語が登場し、その前後の単語の種類・頻度も大きくなることで、各単語の特徴が単語ベクトルに反映されます。
折角なのでテキストに含まれない単語の場合も確認しておきます。
# クエリを指定 query = 'morning' # 類似の単語を表示 most_similar(query, word_to_id, id_to_word, word_matrix, top=5)
morning is not found
以上で類似の高い単語を調べることができました。しかしこのままでは、コーパスが大きくなると別の課題が生じます。次節ではその改善方法を考えます。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 2――自然言語処理編』オライリー・ジャパン,2018年.
おわりに
数式って見慣れない記号を使ったり$n$個の要素を並べたり省略したりするからどうしても仰々しく見えてしまいますけど、$\sqrt{x}$をnp.sqrt(x)、$\sum_{n=1}^N x_n$をnp.sum(x, axis=0)と思えばそこまで恐くなくなると思います。ちなみにLaTeX(Markdown)だと、$\sqrt{x}$は\sqrt{x}、$\sum_{n=1}^N x_n$は\sum_{n=1}^N x_nと書くので、やっぱりどれも似たようなものです(というか同じものです)。
あとはノートにでも書いてみるのもおすすめします。$\sqrt{x_1^2, x_2^2, \cdots, x_n^2}$なんて何度も書いてたら面倒臭くなって、すぐに$\|\mathbf{x}\|$と書きたくなります。
まぁ単なる私の経験談ですが、私はそうやってるうちに慣れました。ちなみにLaTeXだと\|\mathbf{x}\| = \sqrt{x_1^2, x_2^2, \cdots, x_n^2}と書きます。これはどっちにしろ面倒です…。
【次節の内容】