はじめに
『トピックモデルによる統計的潜在意味解析』の学習時のメモです。本と併せて読んでください。
この記事では、3.2.3項のLDAのギブスサンプリングについて書いています。図3.2の疑似コードを基に言語で実装していきます。
プログラムからアルゴリズムの理解を目指します。できるだけ基本的な(直感的理解できる)関数を用いて組んでいきます。
【数理編】
【他の節一覧】
【この節の内容】
3.2.3 LDAのギブスサンプリング
図3.2の疑似コードを参考にLDAに対するギブスサンプリングを実装していきます。
# 利用パッケージ library(tidyverse)
・簡易文書データ(クリックで展開)
## 簡易文書データ # 文書数 M <- 10 # 語彙数 V <- 20 # 文書ごとの各語彙の出現回数 n_dv <- matrix(sample(0:10, M * V, replace = TRUE), M, V)
・パラメータの設定
始めにパラメータ類の初期値を設定していきます。
# サンプリング回数を指定 S <- 1000 # トピック数を指定 K <- 5
サンプリング回数をS、トピックの数をKとします。
# 事前分布のパラメータを指定 alpha_dk <- rep(2, K) %>% # トピック数分の値を指定(本来のパラメータ) rep(each = M) %>% # 文書数ずつ複製 matrix(nrow = M, ncol = K) # マトリクスに変換 beta_kv <- rep(2, V) %>% # 語彙数分の値を指定(本来のパラメータ) rep(each = K) %>% # トピック数ずつ複製 matrix(nrow = K, ncol = V) # マトリクスに変換
トピック分布のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \cdots, \alpha_K)$、単語分布のパラメータ$\boldsymbol{\beta} = (\beta_1, \cdots, \beta_V)$の値をそれぞれ指定します。どちらもディリクレ分布のパラメータなので、$\alpha_k > 0,\ \beta_v > 0$である必要があります。
事前分布のパラメータ$\boldsymbol{\alpha}$はK次元ベクトルですが、事後分布の計算によってM行K列のマトリクス$\boldsymbol{\alpha}^{\mathrm{new}} = (\alpha_{1,1}, \cdots, \alpha_{M,K})$に更新されます。
実装の都合上、この時点で形をそろえておくことにします。(この例では値を一様に設定しているので、matrix()一行で書けますが一応明示しておきます。)
$\boldsymbol{\beta}$についても同様です。
# トピック分布の初期値 theta_dk <- seq(0.01, 1, by = 0.01) %>% sample(size = M * K, replace = TRUE) %>% matrix(nrow = M, ncol = K) # 正規化 theta_dk <- theta_dk / apply(theta_dk, 1, sum) # 単語分布の初期値 phi_kv <- seq(0.01, 1, by = 0.01) %>% sample(size = K * V, replace = TRUE) %>% matrix(nrow = K, ncol = V) # 正規化 phi_kv <- phi_kv / apply(phi_kv, 1, sum)
トピック分布$\boldsymbol{\Theta}$、単語分布$\boldsymbol{\Phi}$の初期値をランダムに設定します。
それぞれ$\sum_{k=1}^K \theta_{d,k} = 1,\ \sum_{v=1}^V \phi_{k,v} = 1$となるように正規化する必要があります。
(値が0だと、後のlog()の計算時にエラーになる。)
# 潜在トピック集合の初期値 z_dvn <- array(0, dim = c(M, V, max(n_dv))) # 各文書において各トピックが割り当てられた単語数の初期値 n_dk <- matrix(0, nrow = M, ncol = K) # 全文書において各トピックが割り当てられた語彙ごとの単語数の初期値 n_kv <- matrix(0, nrow = K, ncol = V)
潜在トピック$\boldsymbol{Z}$の初期値は0(どの単語にもトピックが割り当てられていない状態)とします。なので、各トピックに関する単語数$n_{d,k},\ n_{k,v}$についても初期値は0になります。
語彙(ユニーク単語)ではなく単語(重複した語も別の語として扱う)ごとに潜在トピック$z_{d,i}$を割り当てます(同じ語に対して別のトピックとなることがあります)。しかし語彙ではなく単語だと、文書ごとの総単語数$n_d$が異なる(マトリクスで扱えない)ため扱いづらいです。そこで添字$i$を、$v$と$n$(1からmax(n_dv))に分けて3次元配列として扱うことにします。なので分かりやすいように変数名をz_dvnとします。
それに伴い疑似コードのfor i = 1,...,n_d doの処理を
for(v in 1:V) { ## (各語彙) if(n_dv[d, v] > 0) { ## (出現回数が0のときは行わない) for(n in 1:n_dv[d, v]) { ## (各単語) #z_dvn[d, v, n]のサンプリング } } }
とします。
よってz_dvn[d, v, n]の3次元方向について、各語彙の出現回数より大きい値は初期値0のままとなります。NAではなく0としておくと、後のn_dk, n_kvの計算が楽になります。
# 受け皿を用意 q_z_dv_k <- array(0, dim = c(M, V, K))
添字を使って代入していくには、予めオブジェクトを用意しておく必要があります。
$q(z_{d,i} = k)$はq_z_dv_kとします。これは単語ごとにトピックを割り当てるための確率ですが、計算式(3.29)から分かるように同一単語(語彙)の確率は同じ値となります。(同じ値を記憶する必要もないので)iをvに置き換えて扱うことにします。(また変数名について、頭のq_はz_dvnと見分けやすくするため(事後確率であることを明示するため)、お尻の_kは添字で混乱しないため(オブジェクトの次元を明示するため)です。)
・ギブスサンプリング
続いて推論部分の実装をしていきます。
・コード全体(クリックで展開)
# 推移の確認用 trace_theta <- array(0, dim = c(M, K, S + 1)) trace_phi <- array(0, dim = c(K, V, S + 1)) # 初期値を代入 trace_theta[, , 1] <- theta_dk trace_phi[, , 1] <- phi_kv for(s in 1:S) { ## (イタレーション) # 動作確認用 star_time <- Sys.time() for(d in 1:M) { ## (各文書) for(v in 1:V) { ## (各語彙) if(n_dv[d, v] > 0) { ## (出現回数が0のときは行わない) for(n in 1:n_dv[d, v]) { ## (各単語) # サンプリング確率を計算:式(3.29) tmp_term <- log(phi_kv[, v]) + log(theta_dk[d, ]) q_z_dv_k[d, v, ] <- exp(tmp_term - max(tmp_term)) / sum(exp(tmp_term - max(tmp_term))) # (アンダーフロー対策) # 潜在トピックを割り当て res_z <- rmultinom(n = 1, size = 1, prob = q_z_dv_k[d, v, ]) z_dvn[d, v, n] <- which(res_z == 1) } ## (/各単語) } } ## (/各語彙) # 割り当てられたトピックに関する単語数を更新 for(k in 1:K) { n_dk[d, k] <- sum(z_dvn[d, , ] == k) } # 事後分布のパラメータを更新:式(3.36)の指数部分 alpha_dk[d, ] <- n_dk[d, ] + alpha_dk[d, ] # theta_dをサンプリング theta_dk[d, ] <- MCMCpack::rdirichlet(n = 1, alpha = alpha_dk[d, ]) %>% as.vector() } ## (/各文書) for(k in 1:K) { ## (各トピック) # 割り当てられたトピックに関する単語数を更新 n_kv[k, ] <- apply(z_dvn == k, 2, sum) # 事後分布のパラメータを更新:式(3.37)の指数部分 beta_kv[k, ] <- n_kv[k, ] + beta_kv[k, ] # phi_kをサンプリング phi_kv[k, ] <- MCMCpack::rdirichlet(n = 1, alpha = beta_kv[k, ]) %>% as.vector() } ## (/各トピック) # 推移の確認用 trace_theta[, , s + 1] <- theta_dk trace_phi[, , s + 1] <- phi_kv # 動作確認 #print(paste0(s, "th Sample...", round(Sys.time() - star_time, 3))) }
・$z_{d,i}$のサンプリング
# サンプリング確率を計算:式(3.29) tmp_term <- log(phi_kv[, v]) + log(theta_dk[d, ]) q_z_dv_k[d, v, ] <- exp(tmp_term - max(tmp_term)) / sum(exp(tmp_term - max(tmp_term))) # (アンダーフロー対策)
語彙ごとに、式(3.29)の計算を行います。
ただしデータ数が増えると、各確率値が小さくなるためアンダーフローの可能性があります。そこで対数をとり、次のように計算します。
この$a$を$\boldsymbol{x}$の最大値とすることでアンダーフロー対策になります(これがLogSumExpですか?)。
この確率を基に潜在トピックをサンプリングします。
# 潜在トピックを割り当て res_z <- rmultinom(n = 1, size = 1, prob = q_z_dv_k[d, v, ]) z_dvn[d, v, n] <- which(res_z == 1)
多項分布に従う乱数を生成します。rmultinom()の引数は、1語(size)に1つのトピック(n)を割り当てるのでどちらも1を指定します。
結果はK行1列のマトリクスで返ってくるので、which()を使って値が1となった行を抽出します。その行番号が割り当てられたトピック番号$k$となります。
この処理を各単語に対して行います。
・$\boldsymbol{\theta}_d$のサンプリング
# 割り当てられたトピックに関する単語数を更新 for(k in 1:K) { n_dk[d, k] <- sum(z_dvn[d, , ] == k) }
$n_{d,k}$の定義式は
です。
z_dvn[d, , ]の要素がkである個数がn_dk[d, k]になります。これを1からKまで順番に計算します。(for()を使わずスマートに計算したい…)
この値を使ってハイパーパラメータを更新します。
# 事後分布のパラメータを更新:式(3.36)の指数部分 alpha_dk[d, ] <- n_dk[d, ] + alpha_dk[d, ]
$\boldsymbol{\theta}_d$の事後分布(3.36)(の指数部分)より
の計算を行い、ハイパーパラメータを更新します。ただし2回目のサンプリングからは$\alpha_{d,k}^{(s)} = n_{d,k}^{(s)} + \alpha_{d,k}^{(s-1)}$となります(1つ前の更新値を(この回の)事前分布のパラメータとしています)。
更新したハイパーパラメータを使ってパラメータをサンプリングします。
# theta_dをサンプリング theta_dk[d, ] <- MCMCpack::rdirichlet(n = 1, alpha = alpha_dk[d, ]) %>% as.vector()
デフォルトでディリクレ分布の乱数生成関数はないので、MCMCpackのrdirichlet()を使って$\boldsymbol{\theta}_d$をサンプリングします。結果はマトリクスで返ってくるため、ベクトルに変換しておきます。
この処理を各文書に対して($M$回繰り返し)行います。
・$\boldsymbol{\phi}_k$のサンプリング
# 割り当てられたトピックに関する単語数を更新 n_kv[k, ] <- apply(z_dvn == k, 2, sum)
$n_{k,v}$の定義式は
です。
z_dvn == kとなる要素を語彙(v)ごとに計算します。
この値を使ってハイパーパラメータを更新します。
# 事後分布のパラメータを更新:式(3.37)の指数部分 beta_kv[k, ] <- n_kv[k, ] + beta_kv[k, ]
$\boldsymbol{\phi}_d$の事後分布(3.37)(の指数部分)より
の計算を行い、ハイパーパラメータを更新します。ただし2回目のサンプリングからは$\beta_{k,v}^{(s)} = n_{k,v}^{(s)} + \beta_{k,v}^{(s-1)}$となります(1つ前の更新値を(この回の)事前分布のパラメータとしています)。
更新したハイパーパラメータを使ってパラメータをサンプリングします。
# phi_kをサンプリング phi_kv[k, ] <- MCMCpack::rdirichlet(n = 1, alpha = beta_kv[k, ]) %>% as.vector()
$\boldsymbol{\theta}_d$と同様に、$\boldsymbol{\phi}_k$もサンプリングします。
この処理を各トピックに対して($K$回繰り返し)行います。
・推定結果の確認
ggplot2パッケージを利用して、推定結果を可視化しましょう。
・トピック分布(クリックで展開)
## トピック分布 # 作図用のデータフレームを作成 theta_df_wide <- cbind( as.data.frame(theta_dk), doc = as.factor(1:M) ) # データフレームをlong型に変換 theta_df_long <- pivot_longer( theta_df_wide, cols = -doc, # 変換せずにそのまま残す現列名 names_to = "topic", # 現列名を格納する新しい列の名前 names_prefix = "V", # 現列名から取り除く文字列 names_ptypes = list(topic = factor()), # 現列名を要素とする際の型 values_to = "prob" # 現要素を格納する新しい列の名前 ) # 作図 ggplot(theta_df_long, aes(x = topic, y = prob, fill = topic)) + geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ doc, labeller = label_both) + # グラフの分割 labs(title = "Gibbs Sampler for LDA", subtitle = expression(Theta)) # ラベル
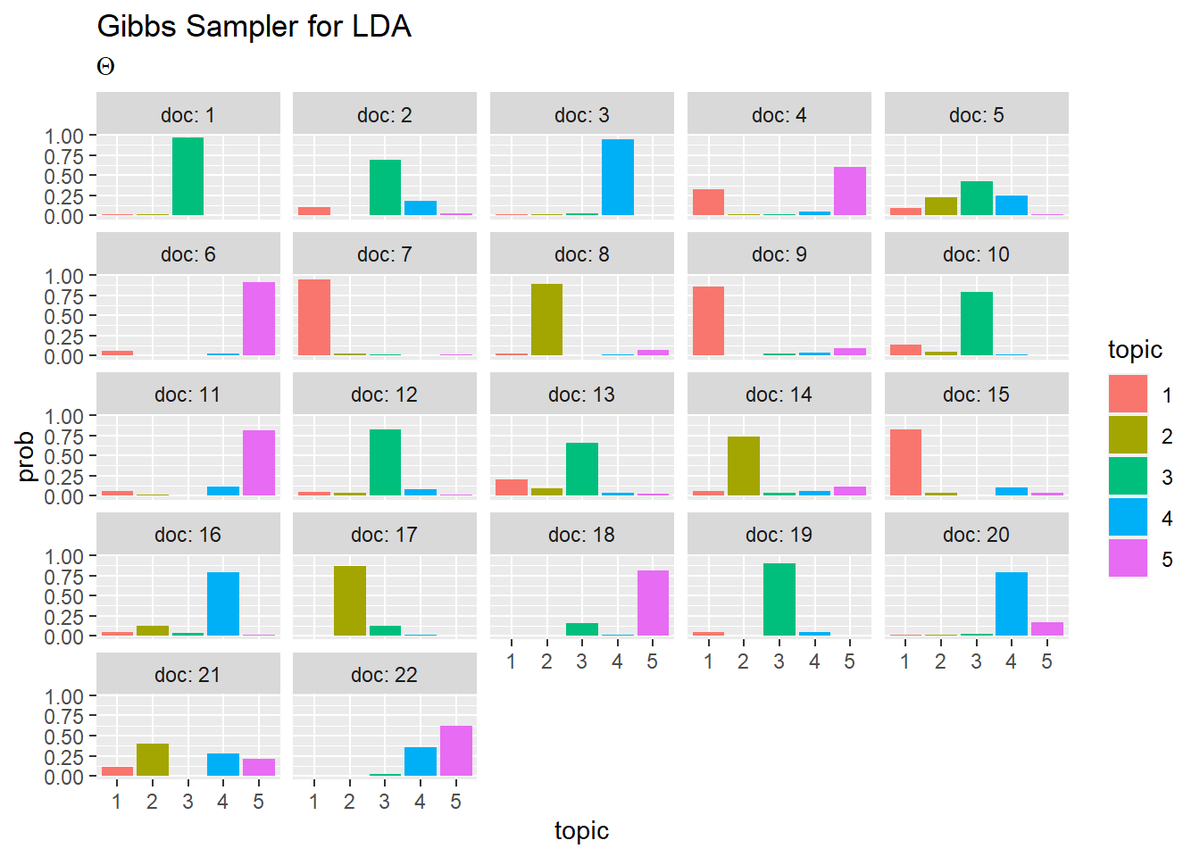
・単語分布(クリックで展開)
## 単語分布 # 作図用のデータフレームを作成 phi_df_wide <- cbind( as.data.frame(phi_kv), topic = as.factor(1:K) ) # データフレームをlong型に変換 phi_df_long <- pivot_longer( phi_df_wide, cols = -topic, # 変換せずにそのまま残す現列名 names_to = "word", # 現列名を格納する新しい列の名前 names_prefix = "V", # 現列名から取り除く文字列 names_ptypes = list(word = factor()), # 現列名を要素とする際の型 values_to = "prob" # 現要素を格納する新しい列の名前 ) # 作図 ggplot(phi_df_long, aes(x = word, y = prob, fill = word, color = word)) + geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ topic, labeller = label_both) + # グラフの分割 scale_x_discrete(breaks = seq(0, V, by = 10)) + # x軸目盛 theme(legend.position = "none") + # 凡例 labs(title = "Gibbs Sampler for LDA", subtitle = expression(Phi)) # ラベル
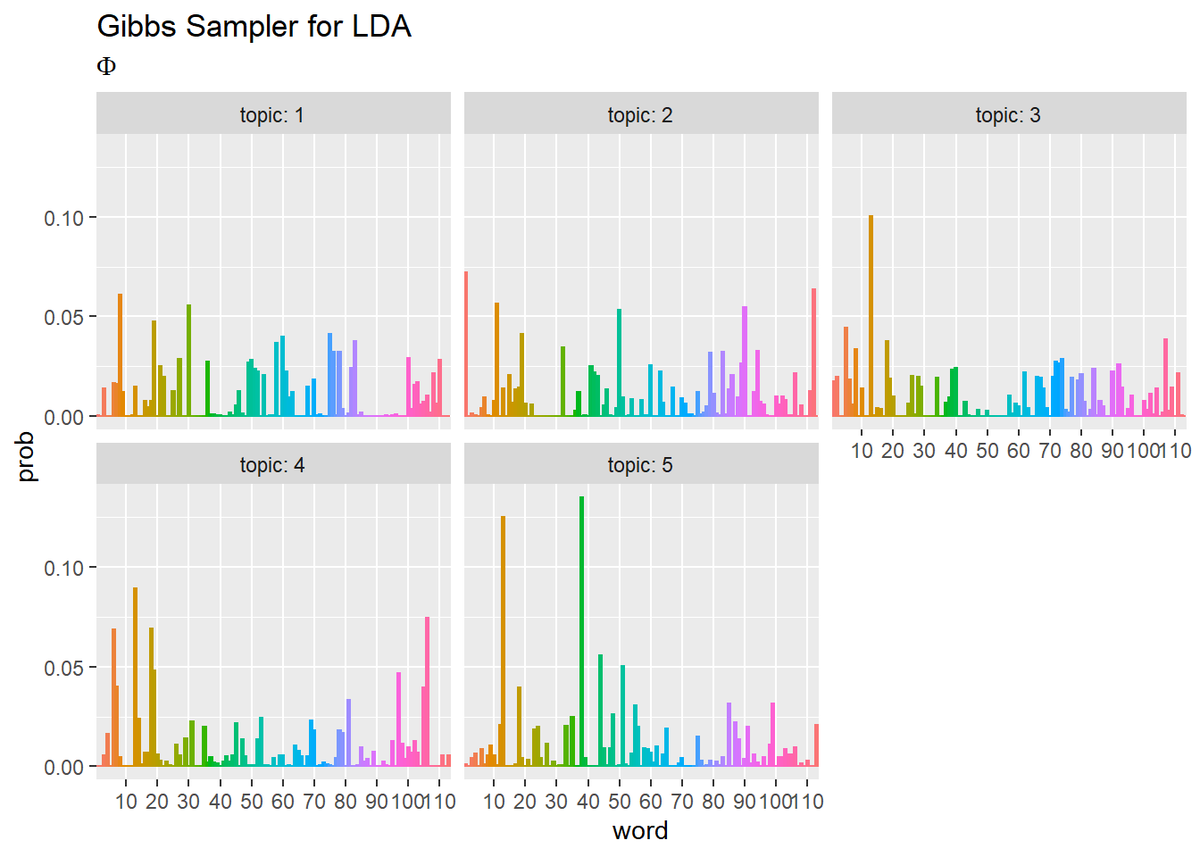
・更新値の推移の確認
・トピック分布(クリックで展開)
## トピック分布 # 作図用のデータフレームを作成 trace_theta_df_wide <- data.frame() for(s in 1:(S + 1)) { # データフレームに変換 tmp_trace_theta <- cbind( as.data.frame(trace_theta[, , s]), doc = as.factor(1:M), # 文書番号 sample = s - 1 # 試行回数 ) # データフレームを結合 trace_theta_df_wide <- rbind(trace_theta_df_wide, tmp_trace_theta) } # データフレームをlong型に変換 trace_theta_df_long <- pivot_longer( trace_theta_df_wide, cols = -c(doc, sample), # 変換せずにそのまま残す現列名 names_to = "topic", # 現列名を格納する新しい列の名前 names_prefix = "V", # 現列名から取り除く文字列 names_ptypes = list(topic = factor()), # 現列名を要素とする際の型 values_to = "prob" # 現要素を格納する新しい列の名前 ) # 文書番号を指定 DocNum <- 5 # 作図 trace_theta_df_long %>% filter(doc == DocNum) %>% ggplot(aes(x = sample, y = prob, color = topic)) + geom_line(alpha = 0.5) + labs(title = "Gibbs Sampler for LDA", subtitle = paste0("d=", DocNum)) # ラベル
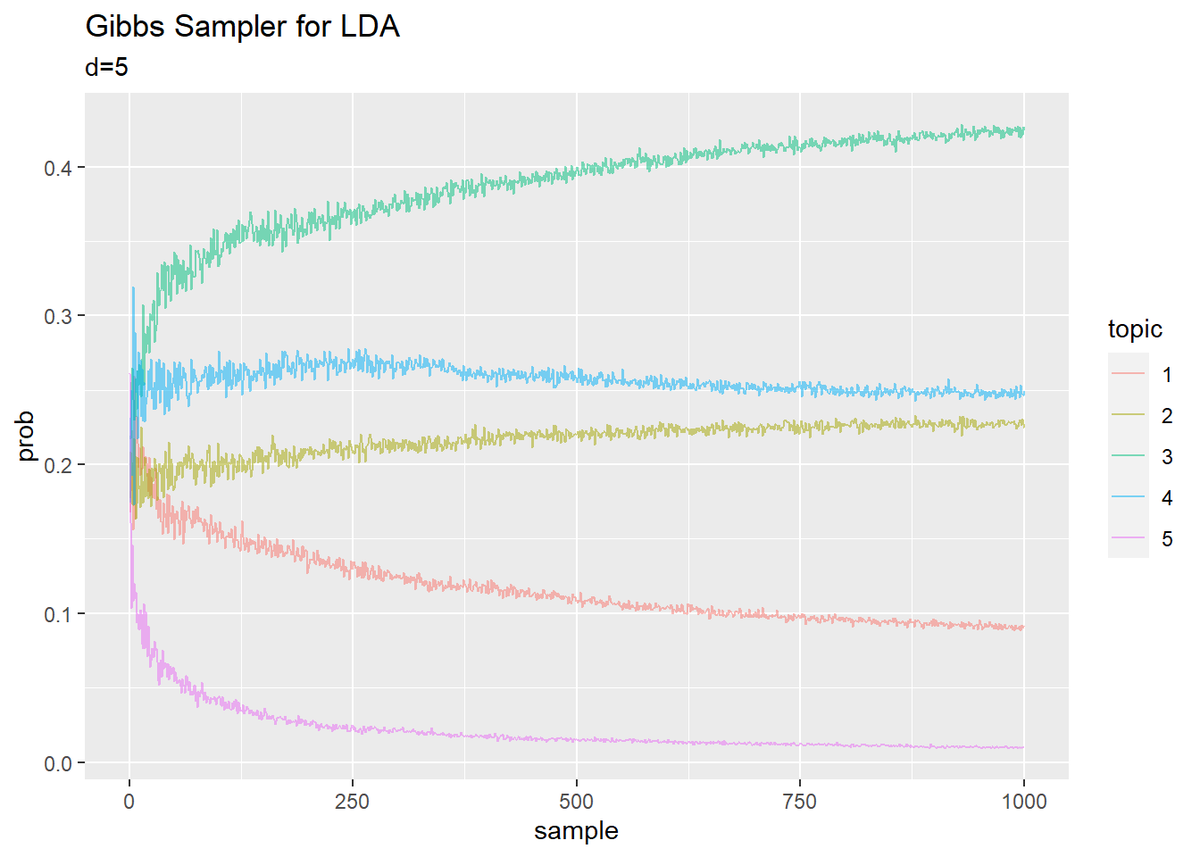
・単語分布(クリックで展開)
## 単語分布 # 作図用のデータフレームを作成 trace_phi_df_wide <- data.frame() for(s in 1:(S + 1)) { # データフレームに変換 tmp_trace_phi <- cbind( as.data.frame(trace_phi[, , s]), topic = as.factor(1:K), # トピック番号 sample = s - 1 # 試行回数 ) # データフレームを結合 trace_phi_df_wide <- rbind(trace_phi_df_wide, tmp_trace_phi) } # データフレームをlong型に変換 trace_phi_df_long <- pivot_longer( trace_phi_df_wide, cols = -c(topic, sample), # 変換せずにそのまま残す現列名 names_to = "word", # 現列名を格納する新しい列の名前 names_prefix = "V", # 現列名から取り除く文字列 names_ptypes = list(word = factor()), # 現列名を要素とする際の型 values_to = "prob" # 現要素を格納する新しい列の名前 ) # トピック番号を指定 TopicNum <- 3 # 作図 trace_phi_df_long %>% filter(topic == TopicNum) %>% ggplot(aes(x = sample, y = prob, color = word)) + geom_line(alpha = 0.2) + theme(legend.position = "none") + # 凡例 labs(title = "Gibbs Sampler for LDA", subtitle = paste0("k=", TopicNum)) # ラベル
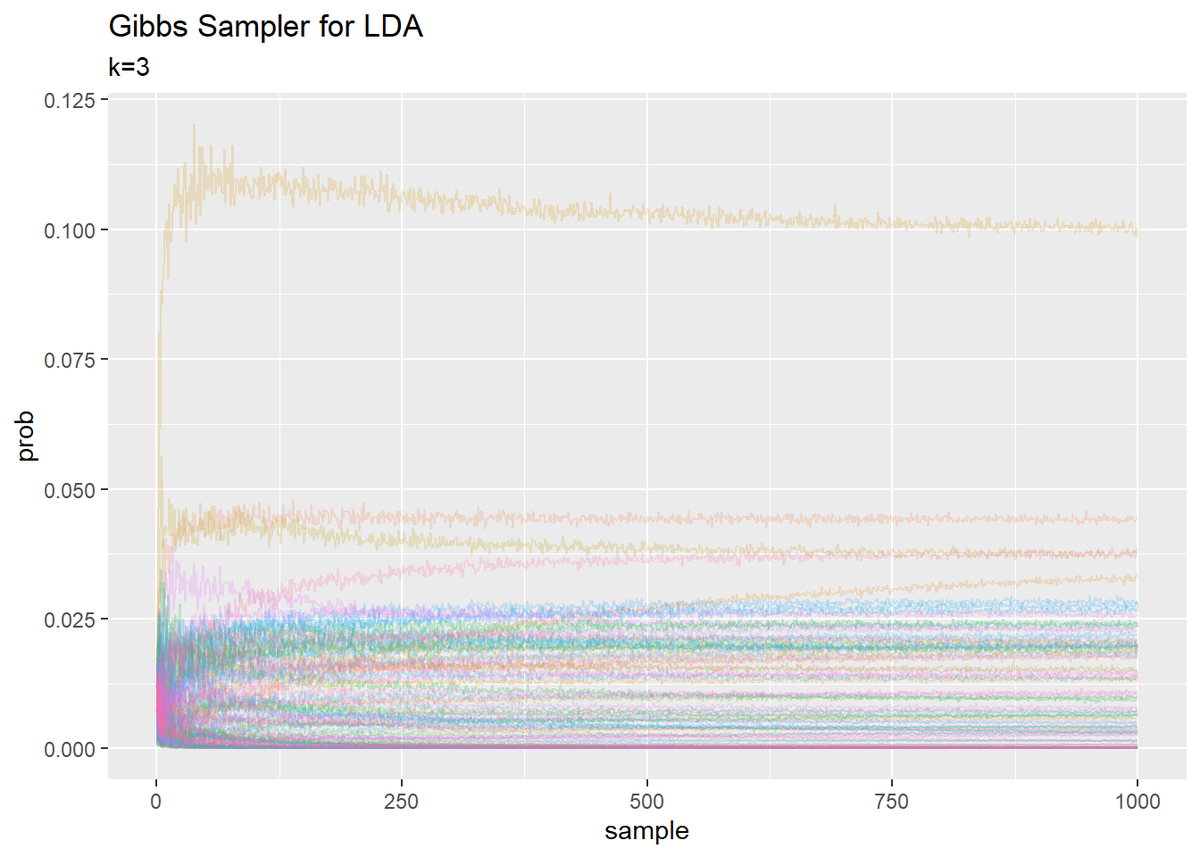
・gif画像を作成
更新ごとの分布の変化をgif画像でみるためのコードです。
・コード(クリックで展開)
gganimateパッケージを利用してgif画像を作成します。上で作成したデータフレームを用います。
# 利用パッケージ library(gganimate) ## トピック分布 # 作図 graph_theta <- ggplot(trace_theta_df_long, aes(x = topic, y = prob, fill = topic)) + geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ doc, labeller = label_both) + # グラフの分割 transition_manual(sample) + # フレーム labs(title = "Gibbs Sampler for LDA", subtitle = "s={current_frame}") # ラベル # gif画像を作成 animate(graph_theta, nframes = S + 1, fps = 10) ## 単語分布 # 作図 graph_phi <- ggplot(trace_phi_df_long, aes(x = word, y = prob, fill = word, color = word)) + geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ topic, labeller = label_both) + # グラフの分割 scale_x_discrete(breaks = seq(0, V, by = 10)) + # x軸目盛 theme(legend.position = "none") + # 凡例 transition_manual(sample) + # フレーム labs(title = "Gibbs Sampler for LDA", subtitle = "s={current_frame}") # ラベル # gif画像を作成 animate(graph_phi, nframes = S + 1, fps = 10)
transition_manual()に時系列値の列を指定します。
(何故か画像をアップロードできないので後程、、、Twitterに上げたのを貼っておくことにしました。。)
LDAのギブスサンプリング:単語分布 pic.twitter.com/oxSolemXKi
— しょこ📚 (@anemptyarchive) 2020年5月22日
参考文献
- 佐藤一誠『トピックモデルによる統計的潜在意味解析』(自然言語処理シリーズ 8)奥村学監修,コロナ社,2015年.
おわりに
2か月以上かかってしまいましたが、何とか出来ました。ゼロから組んでくことひと月(楽しい)、出来てる風ではあるが何か変だをあーだこーだすることひと月(難しい)、ようやく出来たと思われます(気持ちい)。
単純に一般的なギブスサンプリングの理解が足りないのだと気付いたので、理論面の解説が充実しているMCMC本がありましたらお薦めしてほしいです。
ところで、記事ではパラメータの推移を追っていますが、ハイパーパラメータを見る方がいいんですかねぇ、、、
最後まで読んでいただきありがとうございます。言葉を重ねるほどに分かりにくくなっていくこの感じが懐かしい。解説文の方も頑張ります。
May the Force be with you.
【次節の内容】