はじめに
機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に理解の助けになったことや勉強会用レジュメのまとめ記事を書きました。
本で説明されているLDAなどの簡易アルゴリズムを参考にRで組んで推定しました。果たして正しく再現できているのか、検証してみます。
# 利用パッケージ library(tidyverse) set.seed(12)
人工データの作成
トピックの設定
トピックとそのトピックに含まれる単語を用意します。
## 各トピックの単語を指定 # トピック1:色 topic_color <- c( "あお", "あか", "オレンジ", "しろ", "みどり", "もも", "ラベンダー", "レモン", "黄緑", "青緑" ) # トピック2:花 topic_flower <- c( "あやめ", "こぶし", "さくら", "すみれ", "つばき", "マーガレット", "マリーゴールド", "もも", "ゆり", "ラベンダー" ) # トピック3:果物 topic_fruits <- c( "いちご", "オレンジ", "かりん", "さくら", "ぶどう", "バナナ", "メロン", "もも", "りんご", "レモン" ) # トピック4:人の名前 topic_name <- c( "あやか", "かりん", "さくら", "さゆみ", "ちさき", "ほのか", "まなか", "みどり", "もも", "ゆり" )
この例では、4つのトピックを「色」「花」「果物」「人の名前」としました。
そして、トピックに属する単語をそれぞれ10語指定しました。このとき、複数のトピックに含まれる単語も作っておきます。例えば、もも(色)、もも(の花)、(果物の)もも、もも(ちゃん)としています。(分かりにくいかもしれませんがラベンダー(色)やさくら(んぼ)です。被らせるの結構難しいです…)\
続いて、各トピックごとに単語の出現確率を指定します。
## 各トピックの単語の出現確率を指定 # トピック1:色 p_color <- c( 0.05, 0.05, 0.1, 0.2, 0.15, 0.15, 0.1, 0.1, 0.05, 0.05 ) # トピック2:花 p_flower <- c( 0.15, 0.15, 0.12, 0.11, 0.1, 0.1, 0.08, 0.08, 0.06, 0.05 ) # トピック3:果物 p_fruits <- c( 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1 ) # トピック4:人の名前 p_name <- c( 0.06, 0.07, 0.08, 0.09, 0.1, 0.1, 0.11, 0.12, 0.13, 0.14 )
各トピックの値を全て足し合わせると1になるように指定します。出現比率を指定して、その総和で割ることで正規化することもできます。
確率の値もランダムに生成すべきですが、この例では分かりやすさを優先して雰囲気で付けました。
# トピックインデックス k_index <- c("color", "flower", "fruits", "name") # トピック数 K <- 4
ラベル用にトピック名の要素を持つベクトル(トピックインデックス)を作ります。
またトピック数$K$を4としたので、Kに4を代入しておきます。
語彙についても同様に行います。
# 語彙インデックス v_index <- unique(c(topic_color, topic_flower, topic_fruits, topic_name)) # 語彙数 V <- length(v_index)
語彙インデックスの場合は、先ほど作った単語のベクトルをc()で結合します。ただし、語彙は重複を許さない形式であるため、unique()で重複する要素取り除きます。
重複する単語を除いた語彙インデックスの要素数が語彙数$V$であるため、それをVに代入します。
単語分布を作成
トピックごとに単語とその出現確率を設定しました。これを単語分布$\boldsymbol{\Phi}$のマトリクスにしていきます。
まずは、各トピックの単語とトピック名、出現確率が同じ行となるようにデータフレームを作成します。
## 単語分布を作成 # 指定したトピックに関するデータフレームを作成 topic_df_long <- tibble( word = c(topic_color, topic_flower, topic_fruits, topic_name), topic = rep(k_index, each = 10), prob = c(p_color, p_flower, p_fruits, p_name) )
head(topic_df_long) ## # A tibble: 6 x 3 ## word topic prob ## <chr> <chr> <dbl> ## 1 あお color 0.05 ## 2 あか color 0.05 ## 3 オレンジ color 0.1 ## 4 しろ color 0.2 ## 5 みどり color 0.15 ## 6 もも color 0.15
long型のデータフレームができました。これをwide型のデータフレームに変換します。
# wide型のデータフレームに変換 topic_df_wide <- pivot_wider(topic_df_long, names_from = "topic", values_from = "prob") # 変換 topic_df_wide[is.na(topic_df_wide)] <- 0 # NAを0に置換
head(topic_df_wide) ## # A tibble: 6 x 5 ## word color flower fruits name ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 あお 0.05 0 0 0 ## 2 あか 0.05 0 0 0 ## 3 オレンジ 0.1 0 0.1 0 ## 4 しろ 0.2 0 0 0 ## 5 みどり 0.15 0 0 0.12 ## 6 もも 0.15 0.08 0.1 0.13
{tidyr}パッケージ(Ver1.0.0)のpivot_wider()を使ってwide型に変形します。第1引数にデータフレームを渡して、引数names_from = ""に列名とする列を、values_fram = ""に要素とする列を指定します。
該当する要素がない場合にはNAとなるため、これを0に置換します。is.na()によって、NAの位置がTRUEとして返ってきます。それを添え字として用いてNAを抽出し、そこに0を代入しています。
# 単語分布に整形 phi_kv_true <- t(topic_df_wide[, -1]) # 転置 colnames(phi_kv_true) <- topic_df_wide[["word"]] # 列名を各単語にする
phi_kv_true[, 1:10] ## あお あか オレンジ しろ みどり もも ラベンダー レモン 黄緑 青緑 ## color 0.05 0.05 0.1 0.2 0.15 0.15 0.10 0.1 0.05 0.05 ## flower 0.00 0.00 0.0 0.0 0.00 0.08 0.05 0.0 0.00 0.00 ## fruits 0.00 0.00 0.1 0.0 0.00 0.10 0.00 0.1 0.00 0.00 ## name 0.00 0.00 0.0 0.0 0.12 0.13 0.00 0.0 0.00 0.00
最後に、単語分布$\boldsymbol{\Phi}$は$K$行$V$列(行:トピック,列:語彙)の行列であるため、t()で転置して形式を揃えます。また、列名を各語彙としておきます。
これで真の単語分布phi_kv_trueができ上がりました。次は、この単語分布を用いて単語集合を生成していきます。
混合ユニグラムモデル
まずは、混合ユニグラムモデルに従って単語集合を生成することにします。
混合ユニグラムモデルは、文書ごとに1つのトピックを持ちます。そのトピックに従って単語を生成されているとするものです。
この例では、文書数を50とし、また各文書は200語で構成されているとします。
# 文書数を指定 D <- 50 # 単語数を指定(本来のNは全文書での総単語数のこと) N <- 200
文書数$D$に50を、単語数$N$に200を代入しておきます。(本来は$N_d = 200, N = \sum_{d = 1}^D N_d$とすべきところです。)
トピック分布の作成
次は、トピック分布$\boldsymbol{\theta}$を作成します。
# 各トピックの出現確率 theta_k_true <- c(0.15, 0.3, 0.35, 0.2)
混合ユニグラムモデルのトピック分布は$K$個のベクトルです。総和が1となるように各値を指定します。単語分布と同様に、雰囲気で値を決めました。
単語集合の作成
続いて、このトピック分布に従いトピックを生成し、また生成したトピックに従い単語集合を生成します。
# 文書dのトピックの受け皿 z_d_true <- rep(0, D) # 文書dの語彙vの出現回数の受け皿 N_dv <- matrix(0, nrow = D, ncol = V, dimnames = list(paste0("d=", 1:D), v_index)) for(d in 1:D) { # トピックを生成 tmp_z_d <- rmultinom(n = 1, size = 1, prob = theta_k_true) z_d_true[d] <- which(tmp_z_d == 1) k <- z_d_true[d] # 単語を生成 N_dv[d, ] <- rmultinom(n = 1, size = N, prob = phi_kv_true[k, ]) }
N_dv[1:6, 1:10] ## あお あか オレンジ しろ みどり もも ラベンダー レモン 黄緑 青緑 ## d=1 8 13 18 31 29 39 27 20 9 6 ## d=2 0 0 0 0 0 16 8 0 0 0 ## d=3 0 0 0 0 23 27 0 0 0 0 ## d=4 0 0 0 0 0 11 8 0 0 0 ## d=5 0 0 0 0 27 20 0 0 0 0 ## d=6 0 0 0 0 26 22 0 0 0 0
まずは、受け皿として全ての要素が0である$D$行$V$列のマトリクスを作っておきます。そこにfor()を使って、そこにfor()を使って1文書ずつ単語数を代入していきます。
rmultinom()を使って、多項分布に従いトピックをランダムに生成します。引数のn =は試行回数、size =同時に投げるサイコロの数(つまり出現する単語数)、prob =を出現確率です。rmultinom(n = 1, size = 1, prob = theta_k_true)とすると、要素が1つだけ1でそれ以外は0の$K$行1列のマトリクスが返ってきます。
そこから、which()で要素が1の行番号を取り出して、それをこの文書のトピック番号とします。
同様に、単語集合もrmultinom()を使ってを作ります。生成したトピックkを用いて、単語分布phi_kv_trueからトピックkの行($k$番目の行)を取り出し、引数prob =に指定します。また、size = NでN語分の値をランダムに割り振ります。
これを$D$回繰り返し、単語集合$N_{dv}$を完成させます。
# 文書ごとの単語数 N_d <- apply(N_dv, 1, sum)
N_d ## d=1 d=2 d=3 d=4 d=5 d=6 d=7 d=8 d=9 d=10 d=11 d=12 d=13 d=14 d=15 ## 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 ## d=16 d=17 d=18 d=19 d=20 d=21 d=22 d=23 d=24 d=25 d=26 d=27 d=28 d=29 d=30 ## 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 ## d=31 d=32 d=33 d=34 d=35 d=36 d=37 d=38 d=39 d=40 d=41 d=42 d=43 d=44 d=45 ## 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 ## d=46 d=47 d=48 d=49 d=50 ## 200 200 200 200 200
N_dvを行方向に数値をを足し合わせて、文書ごとの単語数を求めます。ここでは全ての文書で200語ずつ単語を生成したので、200を50個持つベクトルが返ってきます。
各文書に割り当てられたトピックについても確認しておきましょう。
z_d_true ## [1] 2 3 3 2 1 3 3 3 4 2 2 3 3 2 3 2 2 3 2 2 4 4 2 2 1 2 1 3 4 4 2 2 2 4 4 ## [36] 3 3 2 2 2 3 2 2 2 3 4 2 3 3 3
table(z_d_true) ## z_d_true ## 1 2 3 4 ## 3 22 17 8
以上でトピック分布と単語分布を作成できたので、グラフにして確認してみましょう。
分布をグラフで確認
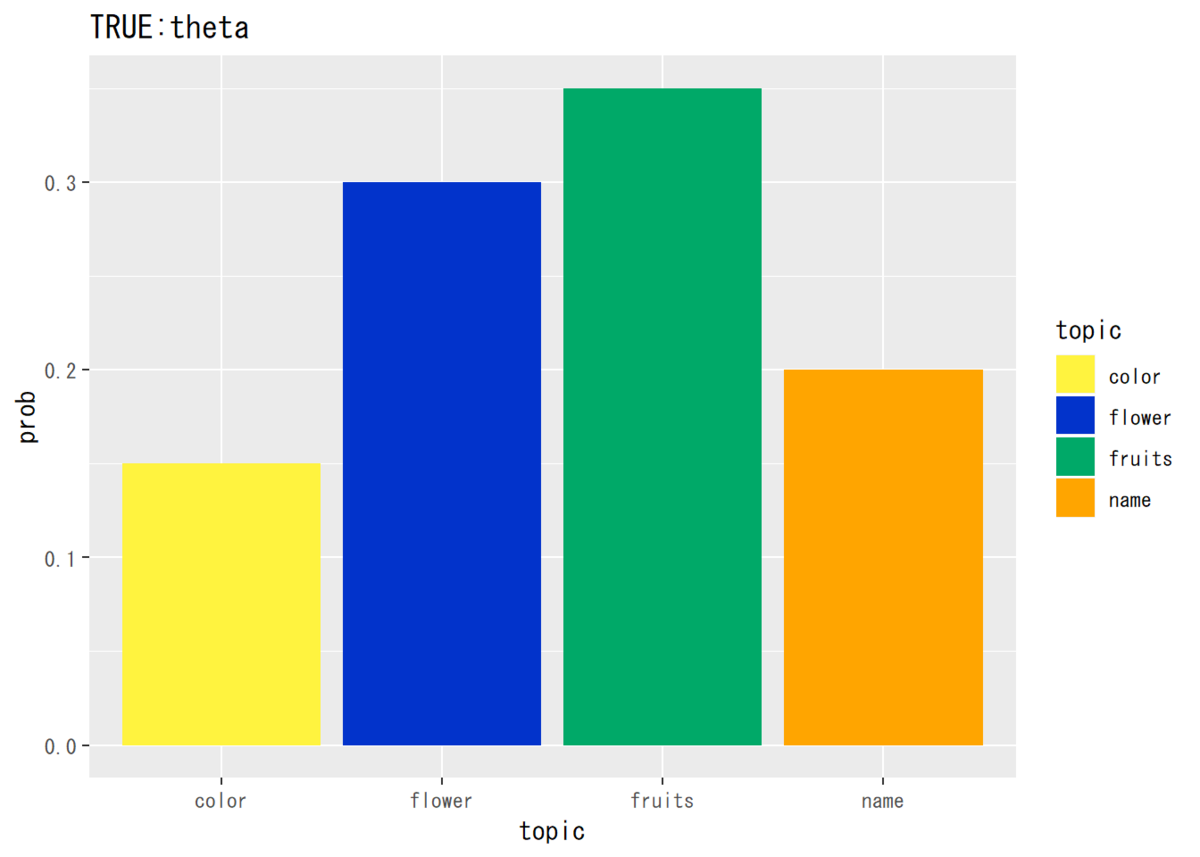
・トピック分布
## トピック分布の推定結果を確認 # データフレームを作成 theta_true_df <- data.frame(topic = k_index, prob = theta_k_true) # 描画 ggplot(theta_true_df, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "TRUE:theta") # タイトル
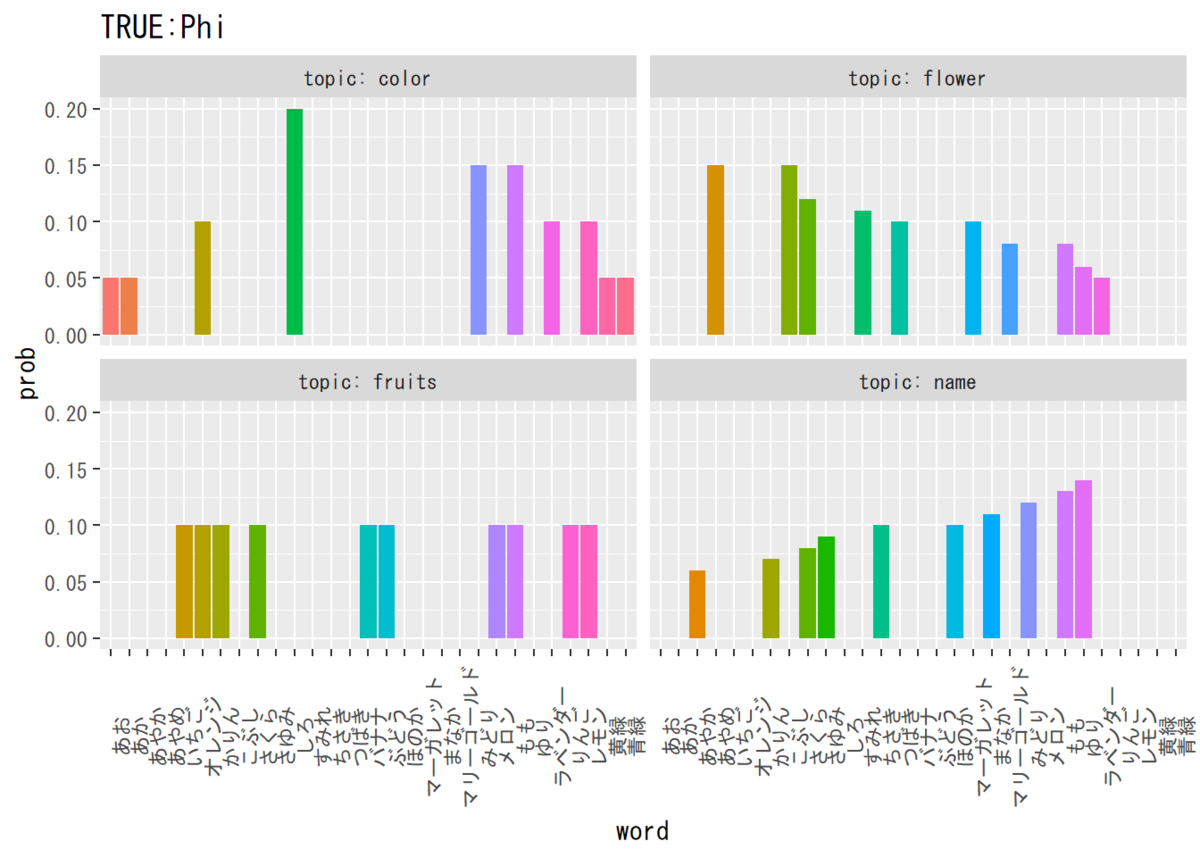
・単語分布
## 単語分布を確認 # データフレームを作成 phi_true_df_wide <- cbind(as.data.frame(phi_kv_true), topic = k_index) # データフレームをlong型に変換 phi_true_df_long <- pivot_longer( phi_true_df_wide, cols = -topic, names_to = "word", values_to = "prob" ) # 描画 ggplot(phi_true_df_long, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap(~ topic, labeller = label_both) + # グラフの分割 theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "TRUE:Phi") # タイトル
これで準備は完了です。では、生成した単語集合$N_{dv}$を用いて各手法で推定した分布と比較していきましょう。
推定
ちなみに推定するトピックの順序はランダムに決まるため推定結果を見ながら判断します。勿論そもそもうまく推定できない可能性も…
混合ユニグラムモデルのEMアルゴリズム
コード(クリックで展開)
# 負担率(q_dk)の集合の受け皿 q_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 ## トピック分布(theta) # 初期値をランダムに設定 theta_k <- sample(seq(0.1, 10, 0.1), size = K, replace = TRUE) # 正規化:sum_{k=1}^K theta_k = 1 theta_k <- theta_k / sum(theta_k) names(theta_k) <- paste0("k=", 1:K) # 確認用の要素名 ## 単語分布(phi) # 初期値をランダムに設定 phi_kv <- sample(seq(0.1, 10, 0.1), size = K * V, replace = TRUE) %>% matrix(nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 v_index)) # 列名 # 正規化 for(k in 1:K) { phi_kv[k, ] <- phi_kv[k, ] / sum(phi_kv[k, ]) } # 最尤推定 for(i in 1:20){ # 次ステップのパラメータを初期化 new_theta_k <- rep(0, K) names(new_theta_k) <- paste0("k=", 1:K) new_phi_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) for(d in 1:D){ ## (各文書:1,...,D) for(k in 1:K){ ## (各トピック:1,...,K) # 負担率の計算 tmp_phi_k <- t(phi_kv) ^ N_dv[d, ] %>% apply(2, prod) q_dk[d, k] <- theta_k[k] * tmp_phi_k[k] / sum(theta_k * tmp_phi_k) # トピック分布(theta_k)を更新 new_theta_k[k] <- new_theta_k[k] + q_dk[d, k] for(v in 1:V){ ## (各語彙:1,...,V) # 単語分布(phi_kv)を更新 new_phi_kv[k, v] <- new_phi_kv[k, v] + q_dk[d, k] * N_dv[d, v] } ## (/各語彙:1,...,V) } ## (/各トピック:1,...,K) } ## (/各文書:1,...,D) # パラメータの更新 theta_k <- new_theta_k phi_kv <- new_phi_kv # パラメータの正規化 theta_k <- theta_k / sum(theta_k) for(k2 in 1:K) { phi_kv[k2, ] <- phi_kv[k2, ] / sum(phi_kv[k2, ]) } }
推定についての詳細はChapter3.3の記事をご参照ください。
・トピック分布
コード(クリックで展開)
## トピック分布の推定結果を確認 # データフレームを作成 theta_df <- data.frame(topic = as.factor(1:K), prob = theta_k) # 描画 ggplot(theta_df, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "Mixture of Unigram Models:MLE:theta") # タイトル
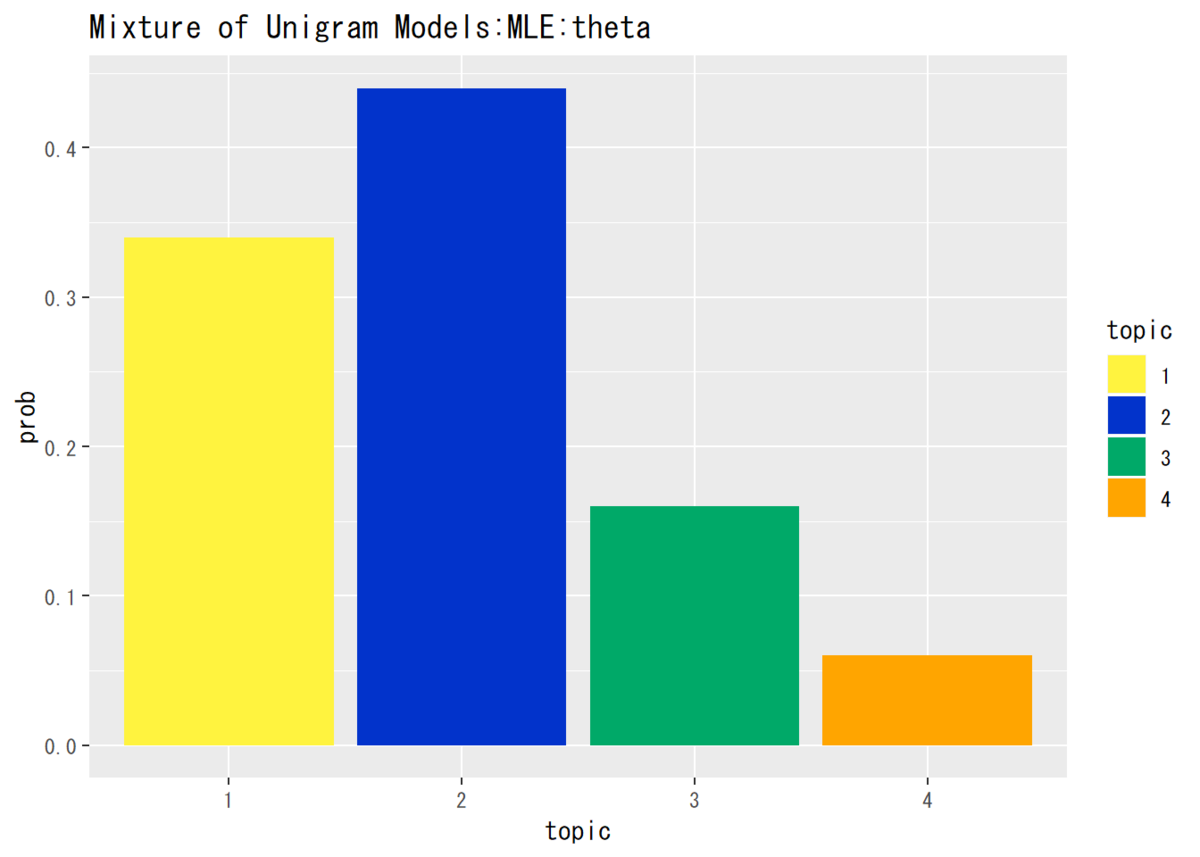
・単語分布
コード(クリックで展開)
## 単語分布を確認 # データフレームを作成 phi_df_wide <- cbind(as.data.frame(phi_kv), topic = as.factor(1:K)) # データフレームをlong型に変換 phi_df_long <- pivot_longer( phi_df_wide, cols = -topic, names_to = "word", values_to = "prob" ) # 描画 ggplot(phi_df_long, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap(~ topic, labeller = label_both) + # グラフの分割 theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "Mixture of Unigram Models:MLE:Phi") # タイトル
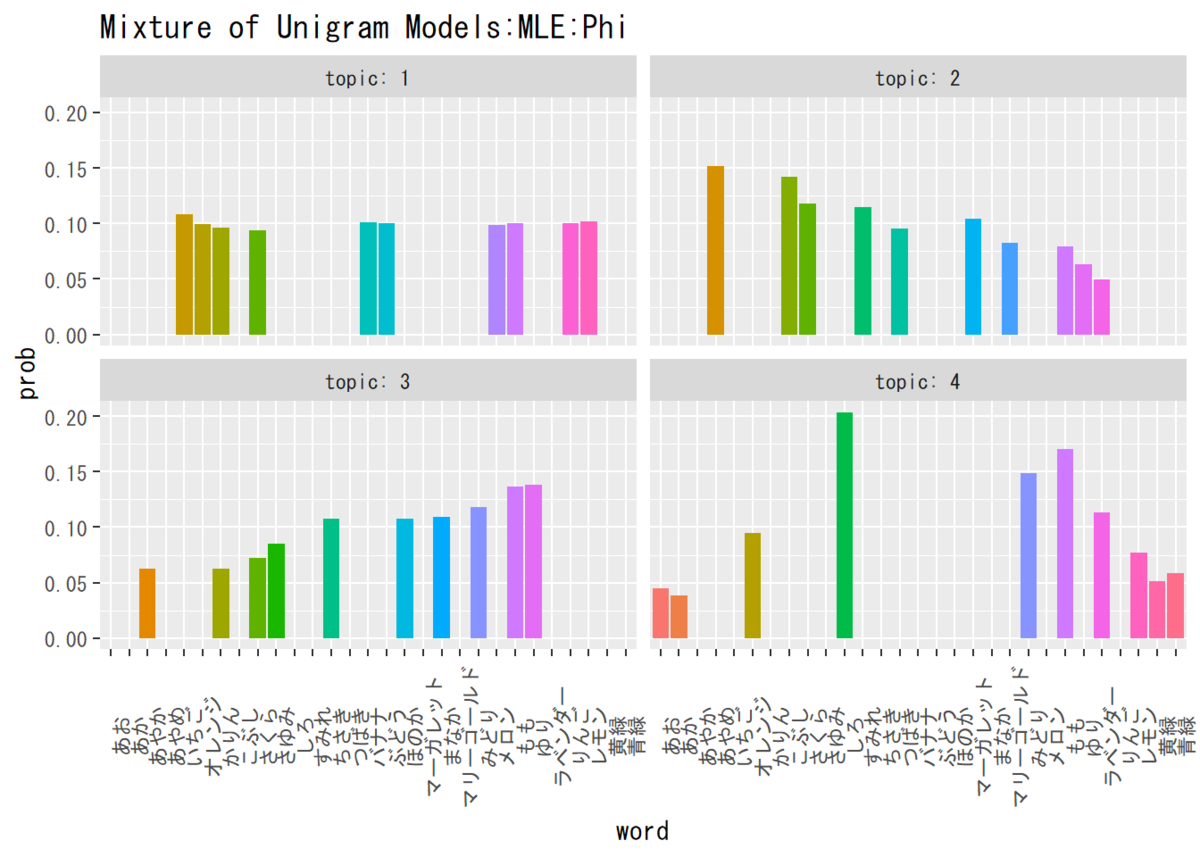
単語分布から見るに、トピック1から「果物」「花」「名前」「色」に対応しているようです。
確率の高い順に「果物」「花」「名前」「色」と設定しましたが、トピック分布をみると「花」「果物」「名前」「色」の順になっています。これは、各文書にランダムに割り当られたトピックの数が「花」の方が多かったことが原因でしょう(z_d_trueを参照)。
かなりの精度で推定できています。こんなにうまくできるものなんですね(感動)。しかしこれを過学習と呼ぶのでしょうか??
という訳でこれはうまく組めたのでしょう。
混合ユニグラムモデルの変分ベイズ推定
コード(クリックで展開)
### パラメータの初期設定 # 負担率(q_dk)の集合 q_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 # 事前分布のパラメータ(α, β) alpha <- 2 # 値を指定する beta <- 2 # 値を指定する # 変分事後分布のパラメータ(α_k)のベクトル alpha_k <- seq(1, 3, 0.1) %>% # 範囲を指定する sample(size = K, replace = TRUE) # 値をランダムに割り振る names(alpha_k) <- paste0("k=", 1:K) # 確認用の要素名 # 変分事後分布のパラメータ(β_kv)の集合 beta_kv <- seq(1, 3, 0.1) %>% # 範囲を指定する sample(size = K * V, replace = TRUE) %>% # 値をランダムに割り振る matrix(nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 v_index)) # 列名 ### 変分ベイズ推定 for(i in 1:20) { # 回数を指定する # 次ステップのハイパーパラメータ(alpha, beta)を初期化 new_alpha_k <- rep(alpha, K) new_beta_kv <- matrix(beta, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) for(d in 1:D){ ## (各文書:1,...,D) for(k in 1:K){ ## (各トピック:1,...,K) # 負担率(q_dk)を計算 tmp_q_alpha <- digamma(alpha_k[k]) - digamma(sum(alpha_k)) tmp_q_beta <- sum(N_dv[d, ] * digamma(beta_kv[k, ])) - N_d[d] * digamma(sum(beta_kv[k, ])) q_dk[d, k] <- exp(tmp_q_alpha + tmp_q_beta) } # 負担率の正規化:sum_{k=1}^K q_dk = 1 if(sum(q_dk[d, ]) > 0) { ## (全ての値が0の場合は回避) q_dk[d, ] <- q_dk[d, ] / sum(q_dk[d, ]) } else if(sum(q_dk[d, ]) == 0) { q_dk[d, ] <- 1 / K } for(k in 1:K) { ## (続き) # ハイパーパラメータ(alpha_k)を更新 new_alpha_k[k] <- new_alpha_k[k] + q_dk[d, k] for(v in 1:V){ ## (各語彙:1,...,V) # ハイパーパラメータ(beta_kv)を更新 new_beta_kv[k, v] <- new_beta_kv[k, v] + q_dk[d, k] * N_dv[d, v] } ## (/各語彙:1,...,V) } ## (/各トピック:1,...,K) } ## (/各文書:1,...,D) # ハイパーパラメータの(alpha, beta)を更新 alpha_k <- new_alpha_k beta_kv <- new_beta_kv }
推定についての詳細はChapter3.4の記事をご参照ください。
・トピック分布$\boldsymbol{\theta}$
コード(クリックで展開)
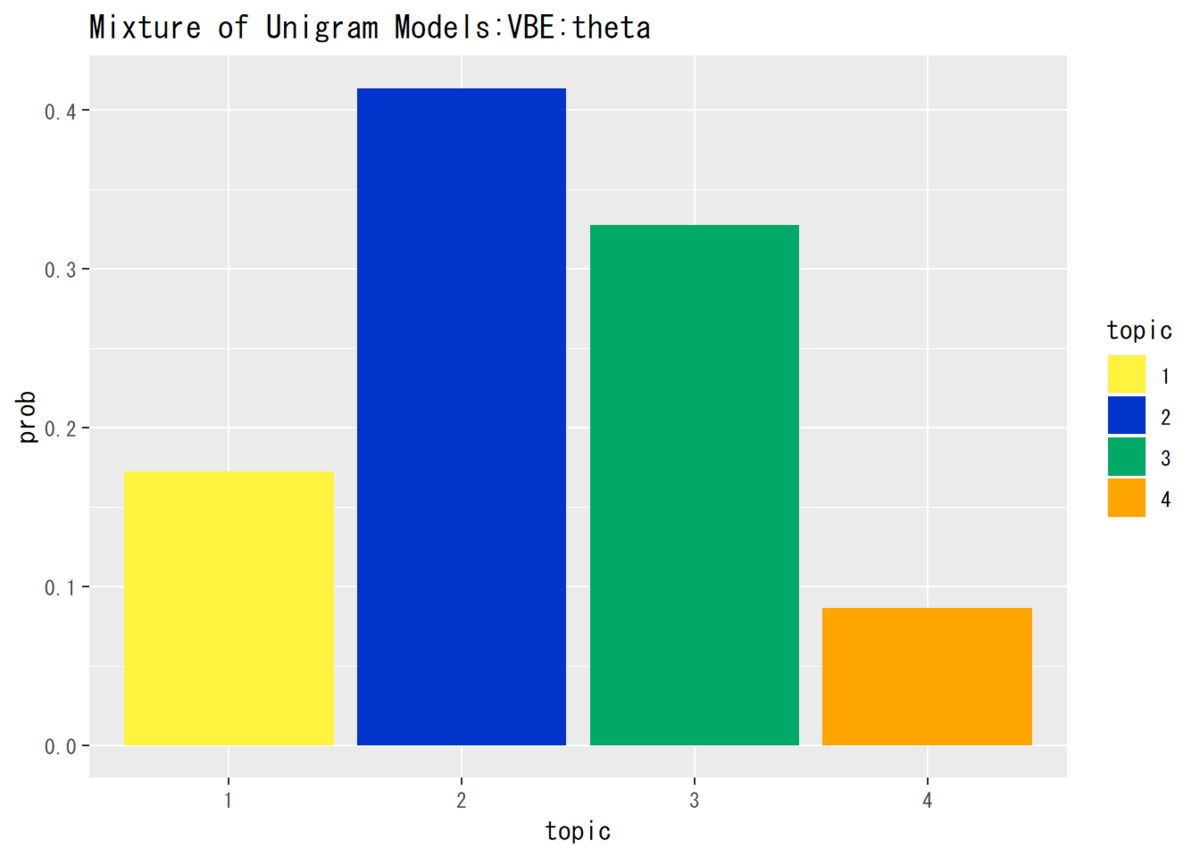
## トピック分布の推定結果(平均値)を確認 # パラメータの平均値を算出 theta_k <- alpha_k / sum(alpha_k) # 平均値を計算 # データフレームを作成 theta_df <- data.frame(topic = as.factor(1:K), prob = theta_k) # 描画 ggplot(theta_df, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "Mixture of Unigram Models:VBE:theta") # タイトル
・単語分布$\boldsymbol{\Phi}$
コード(クリックで展開)
## 単語分布の推定結果(平均値)を確認 # パラメータの平均値を算出 phi_kv <- matrix(nrow = K, ncol = V) for(k in 1:K) { phi_kv[k, ] <- beta_kv[k, ] / sum(beta_kv[k, ]) } # データフレームを作成 phi_df_wide <- cbind(as.data.frame(phi_kv), topic = as.factor(1:K)) colnames(phi_df_wide) <- c(colnames(beta_kv), "topic") # データフレームをlong型に変換 phi_df_long <- pivot_longer( phi_df_wide, cols = -topic, names_to = "word", values_to = "prob" ) # 描画 ggplot(phi_df_long, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap(~ topic, labeller = label_both) + # グラフの分割 theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "Mixture of Unigram Models:VBE:Phi") # タイトル
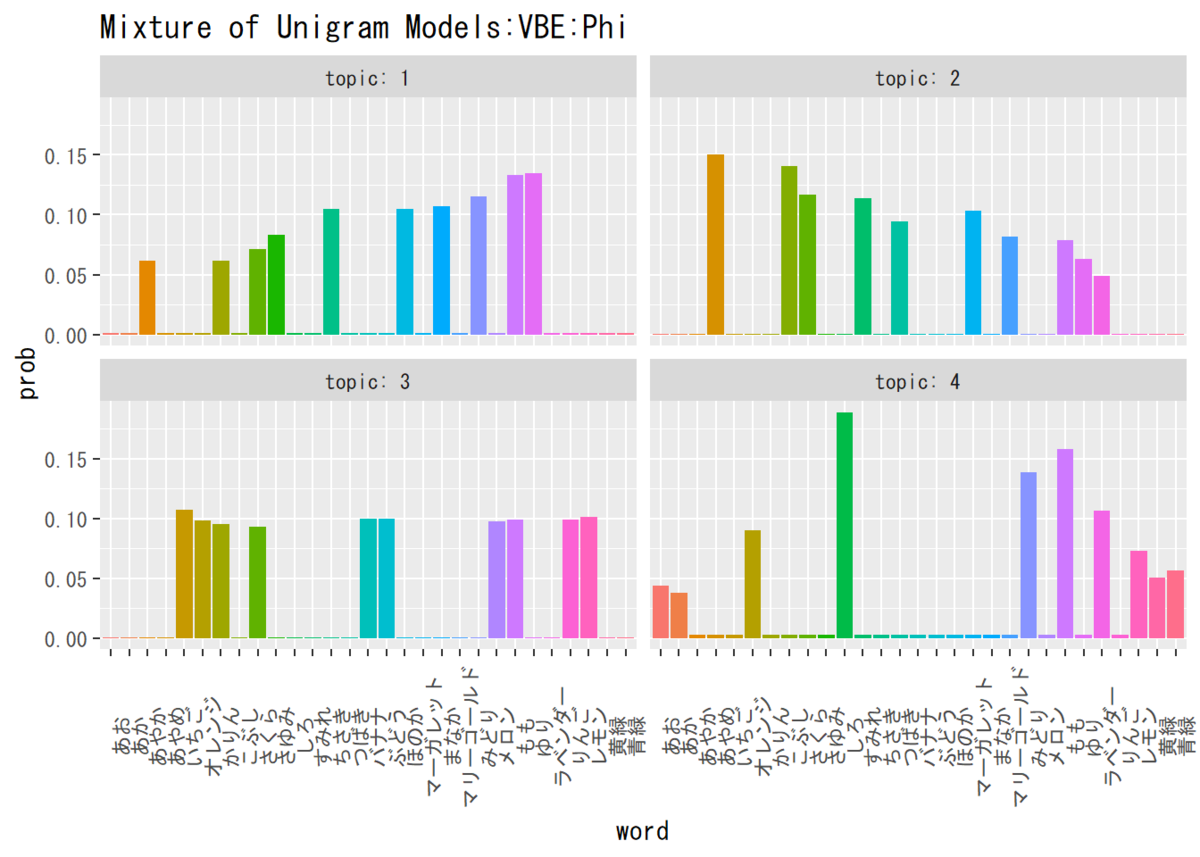
単語分布からみるに、トピック1から「名前」「花」「果物」「色」に対応しているようです。
トピック分析をみると、この手法でも「花」「果物」「名前」「色」の順に高く推定しています。
この手法でもかなりの精度で推定できていますね。最尤推定との違いである、観測が0のデータにもわずかに値が割り振られていることも確認できます。
という訳でこれもうまく組めているのでしょう。
混合ユニグラムモデルのギブスサンプリング
コード(クリックで展開)
### パラメータの初期設定 # ハイパーパラメータ(alpha, beta) alpha <- 2 # 値を指定する beta <- 2 # 値を指定する # トピックkが割り当てられた文書数(D_{z_d})のベクトル D_k <- rep(0, K) # トピックkが割り当てられた文書の語彙vの出現回数(N_{z_d,v})の集合 N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) # トピックkが割り当てられた文書の単語数(N_{z_d})のベクトル N_k <- rep(0, K) # 文書dのトピック(z_d)のベクトル z_d <- rep(0, D) ### ギブスサンプリング # サンプル確率(p) p <- NULL for(i in 1:1000) { # 回数を指定する # 新たに割り当られてるトピックに関するカウントを初期化 new_D_k <- rep(0, K) new_N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) new_N_k <- rep(0, K) for(d in 1:D) { ## (各文書:1,...,D) # 現ステップの計算のために前ステップのカウントを移す tmp_D_k <- D_k tmp_N_kv <- N_kv tmp_N_k <- N_k if(z_d[d] > 0) { # 初回を飛ばす処理 # 前ステップで文書dが与えられたトピックを`k`に代入 k <- z_d[d] # 文書dに関する値をカウントから除く tmp_D_k[k] <- D_k[k] - 1 tmp_N_kv[k, ] <- N_kv[k, ] - N_dv[d, ] tmp_N_k[k] <- N_k[k] - N_d[d] } for(k in 1:K) { ## (各トピック:1,...,K) # サンプリング確率の計算 tmp_p_alpha <- log(tmp_D_k[k] + alpha) # 第1因子 tmp_p_beta1 <- lgamma(tmp_N_k[k] + beta * V) - lgamma(tmp_N_k[k] + N_d[d] + beta * V) # 第2因子 tmp_p_beta2 <- lgamma(tmp_N_kv[k, ] + N_dv[d, ] + beta) - lgamma(tmp_N_kv[k, ] + beta) # 第3因子 p[k] <- exp(tmp_p_alpha + tmp_p_beta1 + sum(tmp_p_beta2)) } ## (/各トピック:1,...,K) # サンプリング tmp_z_d <- rmultinom(n = 1, size = 1, prob = p) # カテゴリ分布によりトピックを生成 z_d[d] <- which(tmp_z_d == 1) # サンプリングの結果を抽出 # 新たに割り当てられたトピックを`k`に代入 k <- z_d[d] # 文書dに関する値をカウントに加える new_D_k[k] <- new_D_k[k] + 1 new_N_kv[k, ] <- new_N_kv[k, ] + N_dv[d, ] new_N_k[k] <- new_N_k[k] + N_d[d] } ## (/各文書:1,...,D) # カウントを更新 D_k <- new_D_k N_kv <- new_N_kv N_k <- new_N_k # ハイパーパラメータ(α)を更新 tmp_alpha_numer <- sum(digamma(D_k + alpha)) - K * digamma(alpha) # 分子 tmp_alpha_denom <- K * digamma(D + alpha * K) - K * digamma(alpha * K) # 分母 alpha <- alpha * tmp_alpha_numer / tmp_alpha_denom # ハイパーパラメータ(β)を更新 tmp_beta_numer <- sum(digamma(N_kv + beta)) - K * V * digamma(beta) # 分子 tmp_beta_denom <- V * sum(digamma(N_k + beta * V)) - K * V * digamma(beta * V) # 分母 beta <- beta * tmp_beta_numer / tmp_beta_denom }
推定についての詳細はChapter3.5の記事をご参照ください。
・トピック分布$\boldsymbol{\theta}$
コード(クリックで展開)
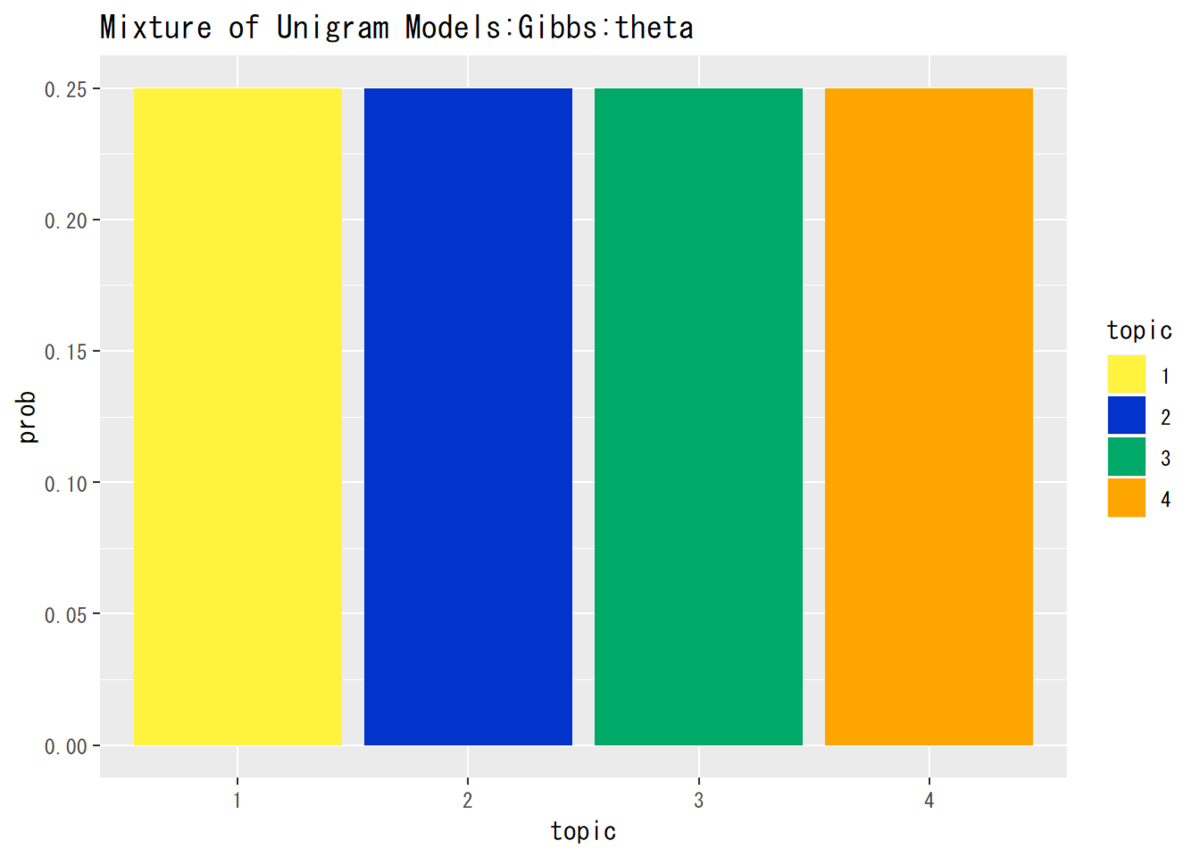
## トピック分布の推定結果(平均値)を確認 # パラメータの平均値を算出 theta_k <- rep(alpha, K) / sum(rep(alpha, K)) # データフレームを作成 theta_df <- data.frame(topic = as.factor(1:K), prob = theta_k) # 描画 ggplot(theta_df, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "Mixture of Unigram Models:Gibbs:theta") # タイトル
・単語分布$\boldsymbol{\phi}$
コード(クリックで展開)
## 単語分布の推定結果(平均値)を確認 # パラメータの平均値を算出 phi_v <- rep(beta, V) / sum(rep(beta, V)) # データフレームを作成 phi_df <- data.frame(word = colnames(N_kv), prob = phi_v) # 描画 ggplot(phi_df, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "Mixture of Unigram Models:Gibbs:phi") # タイトル
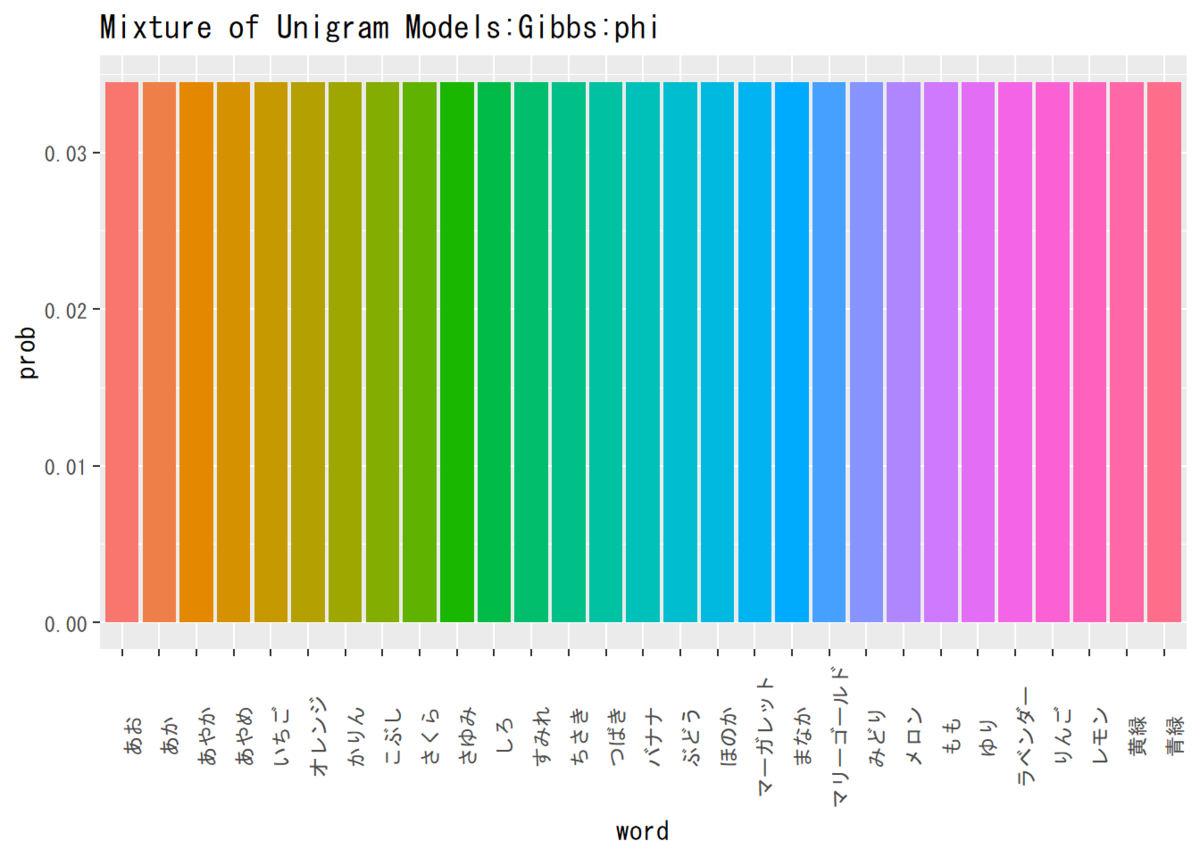
この推定では、パラメータを一様に推定するのでこうなります。多様に推定する方法も導出しておいた方が良いですかね。
ここまでは混合ユニグラムモデルの推定でした。次からはトピックモデルの推定になります。
PLSA
コード(クリックで展開)
### パラメータの初期設定 # 負担率(q_dvk)の集合 q_dvk <- array(0, dim = c(D, V, K), dimnames = list(paste0("d=", 1:D), # 確認用の次元名 v_index, paste0("k=", 1:K))) ## トピック分布(theta_dk)の集合 # 値をランダムに付ける theta_dk <- sample(seq(0.1, 1, 0.01), D * K, replace = TRUE) %>% # ランダムな値を生成 matrix(nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 # 初期値の正規化 for(d in 1:D) { theta_dk[d, ] <- theta_dk[d, ] / sum(theta_dk[d, ]) } ## 単語分布(phi_kv)の集合 # 値をランダムに付ける phi_kv <- sample(seq(0, 1, 0.01), K * V, replace = TRUE) %>% # ランダムな値を生成 matrix(nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 v_index)) # 列名 # 初期値の正規化 for(k in 1:K) { phi_kv[k, ] <- phi_kv[k, ] / sum(phi_kv[k, ]) } ### 最尤推定 for(i in 1:25) { # 回数を指定する # パラメータを初期化 next_theta_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 next_phi_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 v_index)) # 列名 for(d in 1:D) { ## (各文書) for(v in 1:V) { ## (各語彙1) for(k in 1:K) { ## (各トピック) # 負担率を計算 tmp_q_numer <- theta_dk[d, k] * (phi_kv[k, v] ^ N_dv[d, v]) # 分子 tmp_q_denom <- sum(theta_dk[d, ] * (phi_kv[, v] ^ N_dv[d, v])) # 分母 q_dvk[d, v, k] <- tmp_q_numer / tmp_q_denom # theta_dkを更新 next_theta_dk[d, k] <- next_theta_dk[d, k] + q_dvk[d, v, k] * N_dv[d, v] for(v2 in 1:V) { ## (各語彙2) # phi_kvを更新 next_phi_kv[k, v2] <- next_phi_kv[k, v2] + q_dvk[d, v2, k] * N_dv[d, v2] } ## (/各語彙2) } ## (/各トピック) } ## (/各語彙1) } ## (/各文書) # パラメータを更新 theta_dk <- next_theta_dk phi_kv <- next_phi_kv # パラメータを正規化 for(d in 1:D) { theta_dk[d, ] <- theta_dk[d, ] / sum(theta_dk[d, ]) } for(k in 1:K) { phi_kv[k, ] <- phi_kv[k, ] / sum(phi_kv[k, ]) } }
推定についての詳細はChapter4.3の記事をご参照ください。
・トピック分布$\boldsymbol{\Theta}$
コード(クリックで展開)
# データフレームを作成 theta_df_wide <- cbind(as.data.frame(theta_dk), doc = as.factor(1:D)) # データフレームをlong型に変換 colnames(theta_df_wide) <- c(1:K, "doc") theta_df_long <- pivot_longer( theta_df_wide, cols = -doc, names_to = "topic", values_to = "prob" ) # 描画 ggplot(theta_df_long, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ doc, labeller = label_both) + # グラフの分割 scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "PLSA:Theta") # タイトル
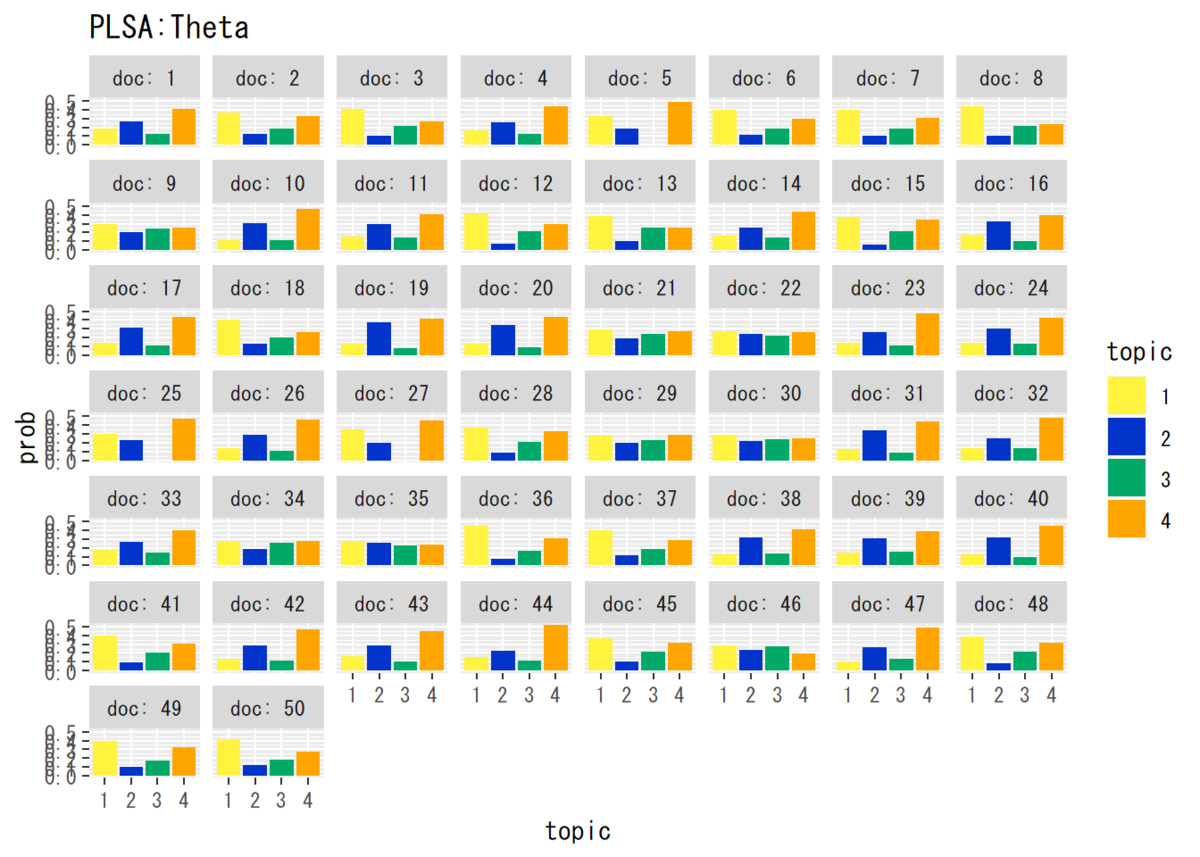
・単語分布$\boldsymbol{\Phi}$
コード(クリックで展開)
# データフレームを作成 phi_df_wide <- cbind(as.data.frame(t(phi_kv)), word = colnames(phi_kv)) # 語彙番号 # データフレームをlong型に変換 colnames(phi_df_wide) <- c(1:K, "word") phi_df_long <- pivot_longer( phi_df_wide, cols = -word, names_to = "topic", values_to = "prob" ) # 描画 ggplot(phi_df_long, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ topic, labeller = label_both) + # グラフの分割 theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "PLSA:Phi") # タイトル
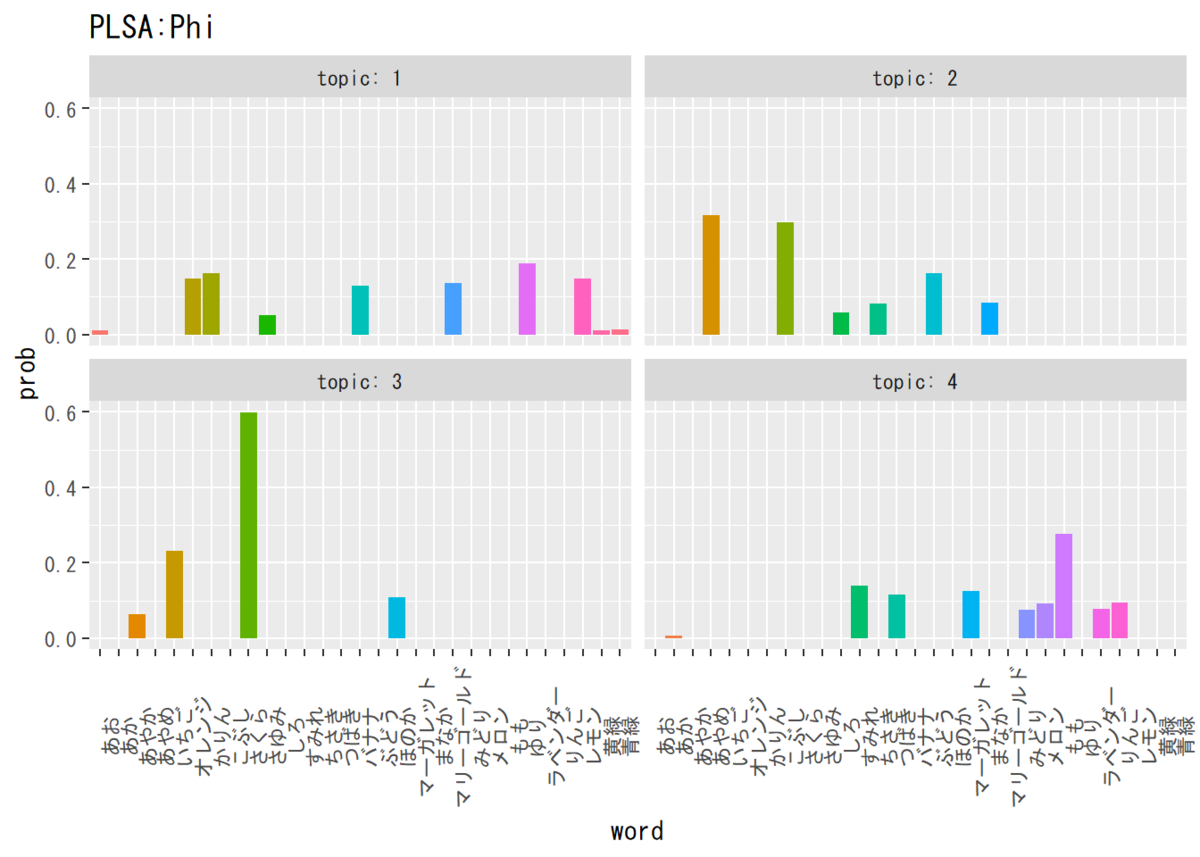
全ての単語が1つのトピックに偏ってしまうことは気付いていたのですが、それだけの問題ではなさそうです。複数のトピックに属さない単語についても推定できていません。
もしかしたら推定したトピック分布と単語分布を用いて単語を生成すれば、元の単語集合を再現できるのかもしれませんが…
という訳で、これは組めていないのでしょう。
LDA
コード(クリックで展開)
### パラメータの初期設 # トピックの変分事後分布(q_dvk)の集合 q_dvk <- array(0, dim = c(D, V, K), dimnames = list(paste0("d=", 1:D), # 確認用の次元名 v_index, paste0("k=", 1:K))) # 事前分布のパラメータ(alpha, beta) alpha <- 2 # 値を指定する beta <- 2 # 値を指定する # トピック分布の変分事後分布のパラメータ(alpha_dk)の集合 alpha_dk <- seq(1, 3, 0.01) %>% # 範囲を指定する sample(D * K, replace = TRUE) %>% # 値をランダムに生成 matrix(nrow = D, ncol = K, # 次元の設定 dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 # 単語分布の変分事後分布のパラメータ(beta_kv)の集合 beta_kv <- seq(1, 3, 0.01) %>% # 範囲を指定する sample(K * V, replace = TRUE) %>% # 値をランダムに生成 matrix(nrow = K, ncol = V, # 次元の設定 dimnames = list(paste0("k=", 1:K), # 行名 v_index)) # 列名 ### 変分ベイズ推定 for(i in 1:20) { # パラメータを初期化 new_alpha_dk <- matrix(data = alpha, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) new_beta_kv <- matrix(data = beta, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) for(d in 1:D) { ## (各文書) for(v in 1:V) { ## (各語彙) for(k in 1:K) { ## (各トピック) # 負担率(q_dvk)を計算 tmp_q_alpha <- digamma(alpha_dk[d, k]) - digamma(sum(alpha_dk[d, ])) tmp_q_beta <- N_dv[d, v] * (digamma(beta_kv[k, v]) - digamma(sum(beta_kv[k, ]))) q_dvk[d, v, k] <- exp(tmp_q_alpha + tmp_q_beta) } # 負担率を正規化 q_dvk[d, v, ] <- q_dvk[d, v, ] / sum(q_dvk[d, v, ]) for(k in 1:K) { ## (各トピック(続き)) # alpha_dkを更新 new_alpha_dk[d, k] <- new_alpha_dk[d, k] + q_dvk[d, v, k] # beta_kvを更新 new_beta_kv[k, v] <- new_beta_kv[k, v] + q_dvk[d, v, k] * N_dv[d, v] } ## (/各トピック) } ## (/各語彙) } ## (/各文書) # パラメータを更新 alpha_dk <- new_alpha_dk beta_kv <- new_beta_kv }
推定についての詳細はChapter4.4の記事をご参照ください。
・トピック分布$\boldsymbol{\Theta}$
コード(クリックで展開)
## トピック分布の推定結果(平均値)を確認 # パラメータの平均値を算出 theta_dk <- matrix(nrow = D, ncol = K) for(d in 1:D) { theta_dk[d, ] <- alpha_dk[d, ] / sum(alpha_dk[d, ]) } # データフレームを作成 theta_df_wide <- cbind(as.data.frame(theta_dk), as.factor(1:D)) # 文書番号の列を加える # データフレームをlong型に変換 colnames(theta_df_wide) <- c(1:K, "doc") # key用に行名を付与 theta_df_long <- pivot_longer( theta_df_wide, cols = -doc, names_to = "topic", values_to = "prob" ) # 作図 ggplot(theta_df_long, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap(~ doc, labeller = label_both) + # グラフの分割 scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "LDA:Theta") # タイトル
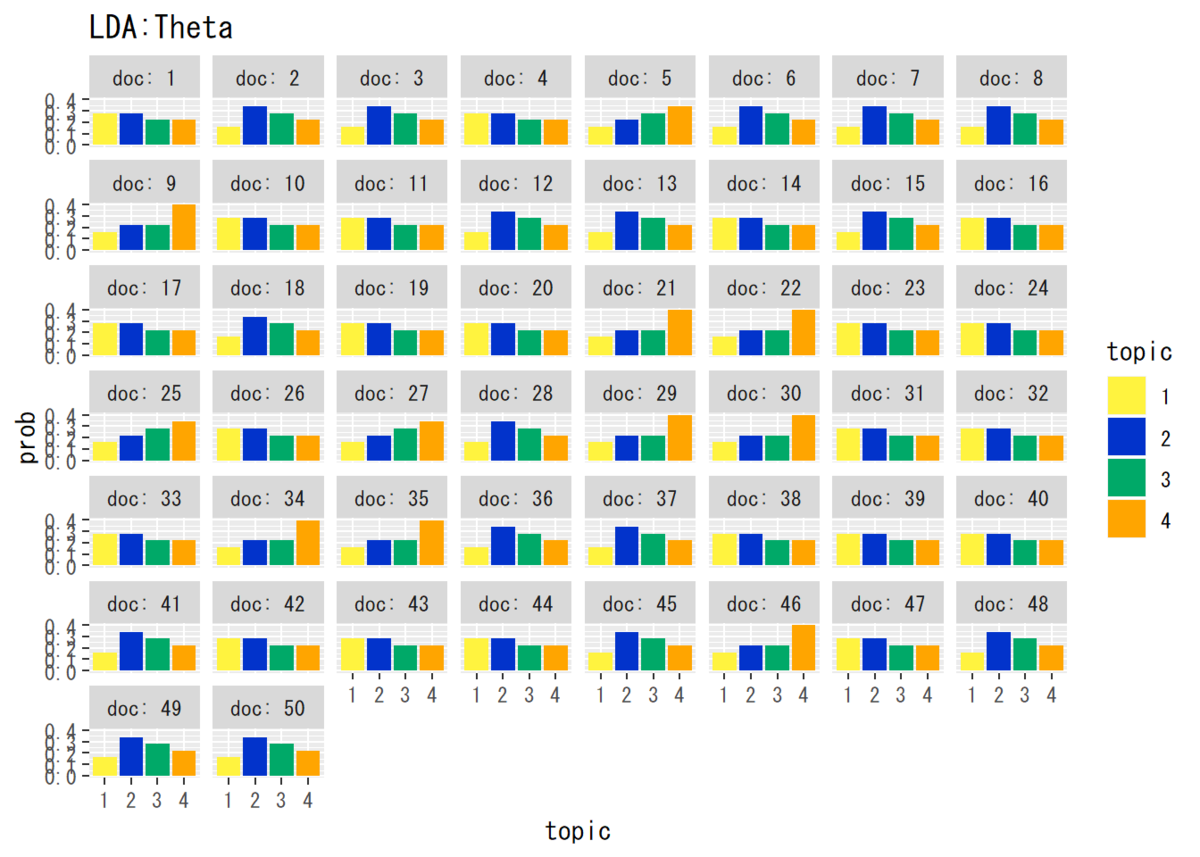
・単語分布$\boldsymbol{\Phi}$
コード(クリックで展開)
## 単語分布の推定結果(平均値)を確認 # パラメータの平均値を算出 phi_kv <- matrix(nrow = K, ncol = V) for(k in 1:K) { phi_kv[k, ] <- beta_kv[k, ] / sum(beta_kv[k, ]) } # データフレームを作成 phi_df_wide <- cbind(as.data.frame(phi_kv), topic = as.factor(1:K)) colnames(phi_df_wide) <- c(colnames(beta_kv), "topic") # データフレームをlong型に変換 phi_df_long <- pivot_longer( phi_df_wide, cols = -topic, names_to = "word", values_to = "prob" ) # 描画 ggplot(phi_df_long, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap(~ topic, labeller = label_both) + # グラフの分割 theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "LDA:Phi") # タイトル
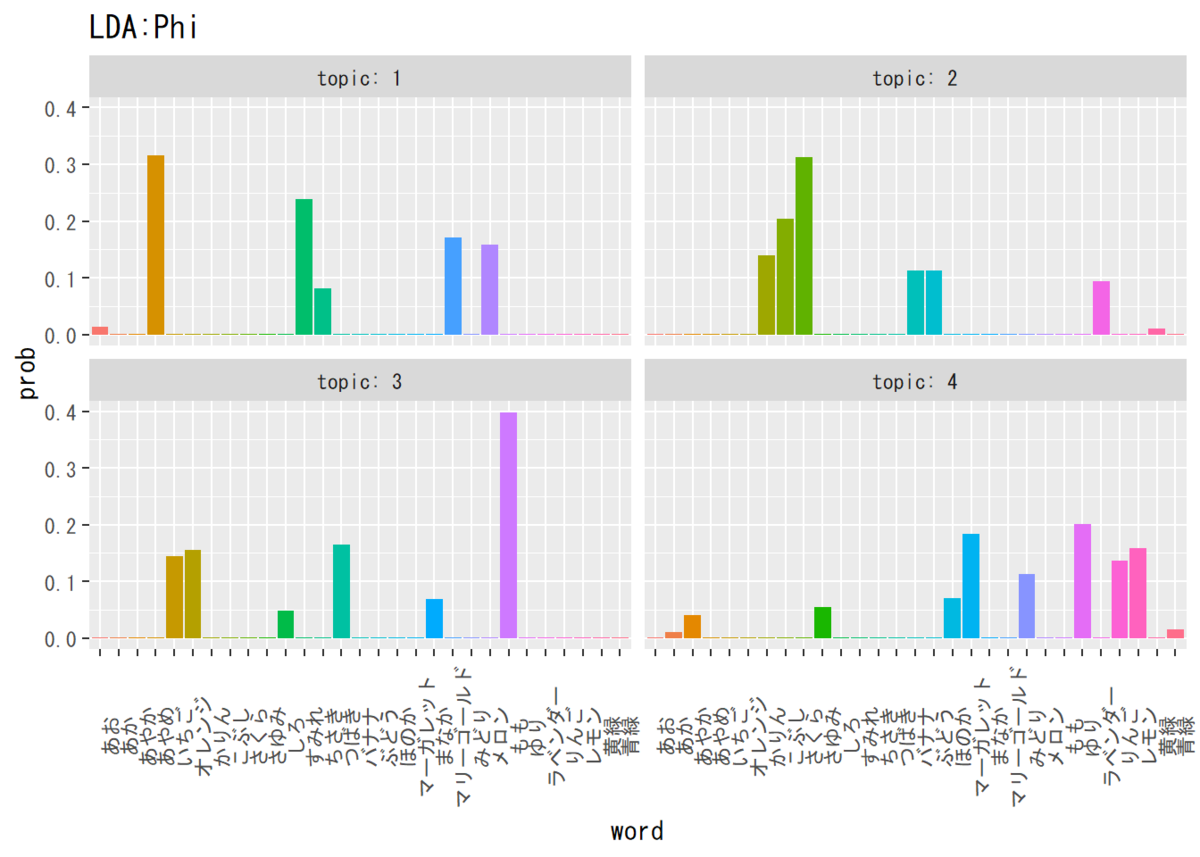
同上…
ギブスサンプリング
コード(クリックで展開)
### パラメータの初期設定 # ハイパーパラメータ(alpha, beta) alpha_k <- rep(2, K) # 値を指定する beta <- 2 # 値を指定する # 文書dの語彙vに割り当てられたトピック(z_dn)の集合 z_dn <- array(0, dim = c(D, V, max(N_dv)), dimnames = list(paste0("d=", 1:D), v_index, paste0("N_dv=", 1:max(N_dv)))) # 文書dにおいてトピックkが割り当てられた単語数(N_dk)の集合 N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) # 文書全体でトピックkが割り当てられた語彙vの出現回数(N_kv)の集合 N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) # 全文書でトピックkが割り当てられた単語数(N_k)のベクトル N_k <- rep(0, K) ### ギブスサンプリング # 受け皿の用意 p <- NULL for(i in 1:1000) { ## 新たに割り当られたトピックに関するカウントを初期化 new_N_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), paste0("k=", 1:K))) new_N_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), v_index)) new_N_k <- rep(0, K) for(d in 1:D) { ## 文書:1,...,D for(v in 1:V) { ## 各語彙:1,...,V if(N_dv[d, v] > 0) { ## 出現回数:N_dv > 0のときのみ for(ndv in 1:N_dv[d, v]) { ## 各語彙の出現回数:1,...,N_dv # 現ステップの計算のためにカウントを移す tmp_N_dk <- N_dk tmp_N_kv <- N_kv tmp_N_k <- N_k if(z_dn[d, v, ndv] > 0) { # 初回を飛ばす処理 # 前ステップで文書dの語彙vに割り当てられたトピックを`k`に代入 k <- z_dn[d, v, ndv] # 文書dの語彙vの分のカウントを引く tmp_N_dk[d, k] <- N_dk[d, k] - 1 tmp_N_kv[k, v] <- N_kv[k, v] - 1 tmp_N_k[k] <- N_k[k] - 1 } for(k in 1:K) { ## 各トピック # サンプリング確率を計算 tmp_p_alpha <- tmp_N_dk[d, k] + alpha_k[k] tmp_p_beta_numer <- tmp_N_kv[k, v] + beta tmp_p_beta_denom <- tmp_N_k[k] + beta * V p[k] <- tmp_p_alpha * tmp_p_beta_numer / tmp_p_beta_denom } # サンプリング tmp_z_dn <- rmultinom(n = 1, size = 1:K, prob = p) z_dn[d, v, ndv] <- which(tmp_z_dn == 1) # 新たに割り当てられたトピックを`k`に代入 k <- z_dn[d, v, ndv] # 文書dの語彙vの分のカウントを加える new_N_dk[d, k] <- new_N_dk[d, k] + 1 new_N_kv[k, v] <- new_N_kv[k, v] + 1 new_N_k[k] <- new_N_k[k] + 1 } ## /各語彙の出現回数:1,...,N_dv } ## /出現回数:N_dv > 0のときのみ } ## /各語彙:1,...,V } ## /各文書:1,...,D # トピック集合とカウントを更新 N_dk <- new_N_dk N_kv <- new_N_kv N_k <- new_N_k # ハイパーパラメータ(alpha)の更新 tmp_alpha_numer1 <- apply(digamma(t(N_dk) + alpha_k), 1, sum) # 分子 tmp_alpha_numer2 <- D * digamma(alpha_k) # 分子 tmp_alpha_denom1 <- sum(digamma(N_d + sum(alpha_k))) # 分母 tmp_alpha_denom2 <- D * digamma(sum(alpha_k)) # 分母 alpha_k <- alpha_k * (tmp_alpha_numer1 - tmp_alpha_numer2) / (tmp_alpha_denom1 - tmp_alpha_denom2) # ハイパーパラメータ(beta)の更新 tmp_beta_numer1 <- sum(digamma(N_kv + beta)) # 分子 tmp_beta_numer2 <- K * V * digamma(beta) # 分子 tmp_beta_denom1 <- V * sum(digamma(N_k + beta * V)) # 分母 tmp_beta_denom2 <- K * V * digamma(beta * V) # 分母 beta <- beta * (tmp_beta_numer1 - tmp_beta_numer2) / (tmp_beta_denom1 - tmp_beta_denom2) }
推定についての詳細はChapter4.5の記事をご参照ください。
・トピック分布$\boldsymbol{\theta}$
コード(クリックで展開)
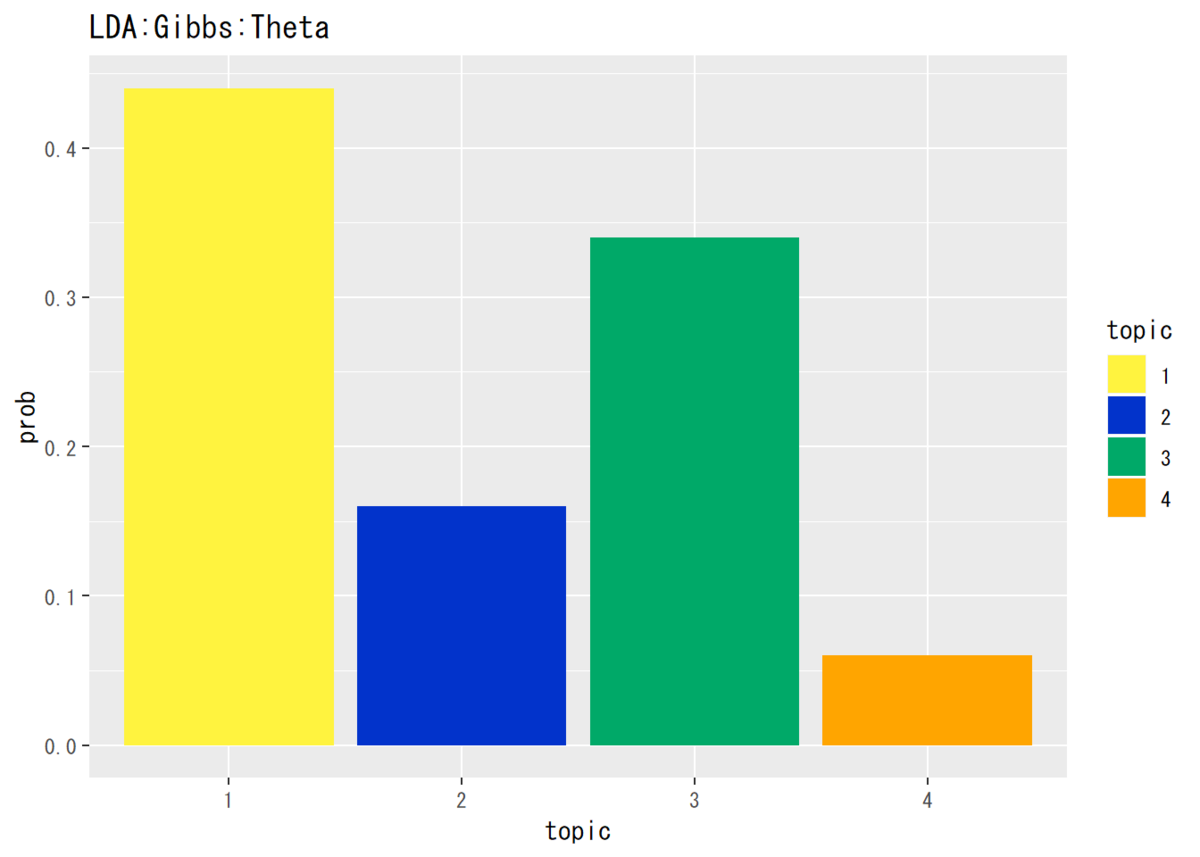
## トピック分布(平均値)の確認 # データフレームを作成 theta_df <- data.frame(topic = as.factor(1:K), prob = alpha_k / sum(alpha_k)) # 描画 ggplot(theta_df, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 折れ線グラフ scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "LDA:Gibbs:Theta") # タイトル
・単語分布$\boldsymbol{\phi}$
コード(クリックで展開)
## 単語分布の推定結果(平均値)を確認 # パラメータの平均値を算出 phi_v <- rep(beta, V) / sum(rep(beta, V)) # データフレームを作成 phi_df <- data.frame(word = colnames(N_kv), prob = phi_v) # 描画 ggplot(phi_df, aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ theme(legend.position = "none", # 凡例 axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "LDA:Gibbs:phi") # タイトル
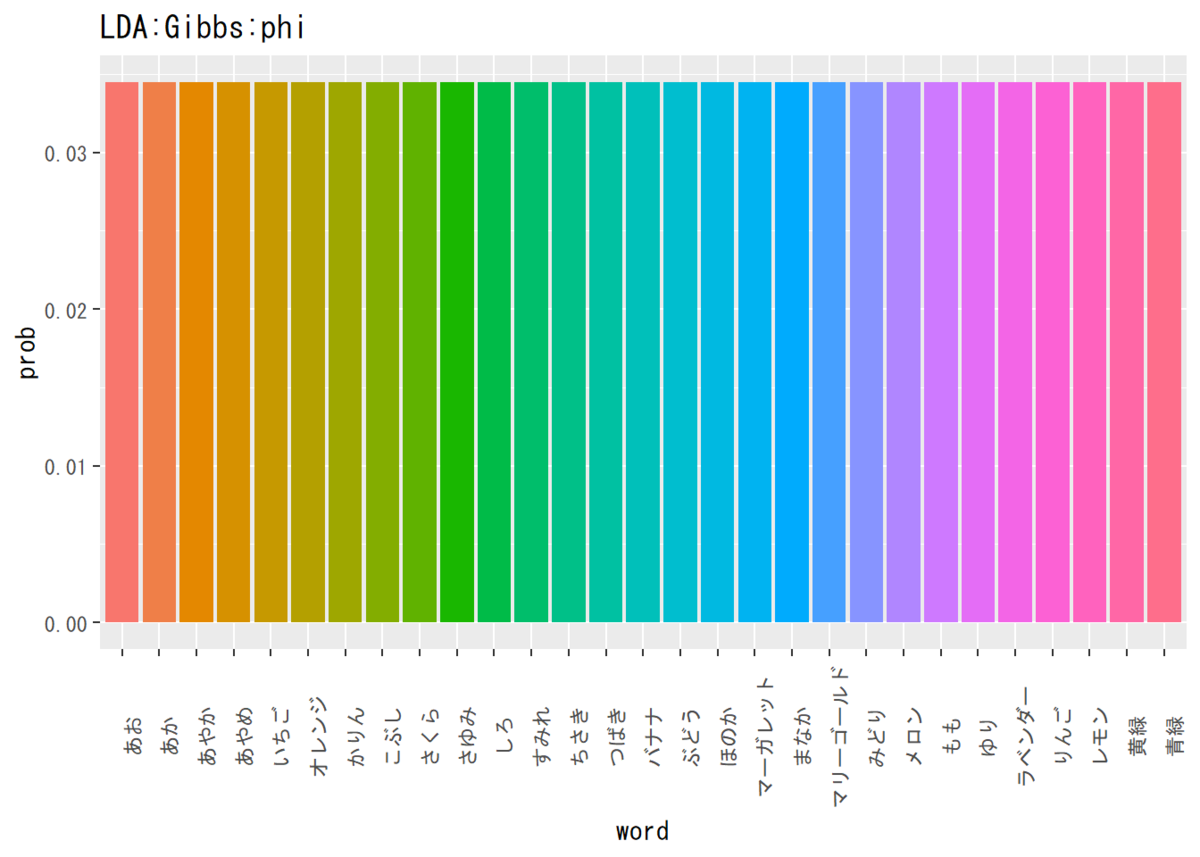
トピック分布の形は近そうな感じですが、単語分布は一様に推定するので何とも言えません。
今度は、トピックモデルに従って単語集合を生成し、それを使って推定していきます。
トピックモデル
トピックモデルは、文書ごとに複数のトピックを重みを付けて持ちます。そのトピック分布に従って各単語のトピックが決まり、そのトピックが持つ単語分布に従って具体的な単語が生成されているとするものです。
トピック分布の作成
トピック分布のパラメータ$\boldsymbol{\alpha}$を指定します。
# ハイパーパラメータを生成 alpha_k_true <- c(1, 3, 4, 2)
$\alpha_k ,\ (k = 1, \cdots, K)$は1以上の値を雰囲気で指定します。
グラフで確認します。
## トピック分布のパラメータ # データフレームを作成 alpha_true_df <- data.frame(value = alpha_k_true, topic = k_index) # 作図 ggplot(alpha_true_df, aes(x = topic, y = value, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 labs(title = "TRUE:alpha") # タイトル
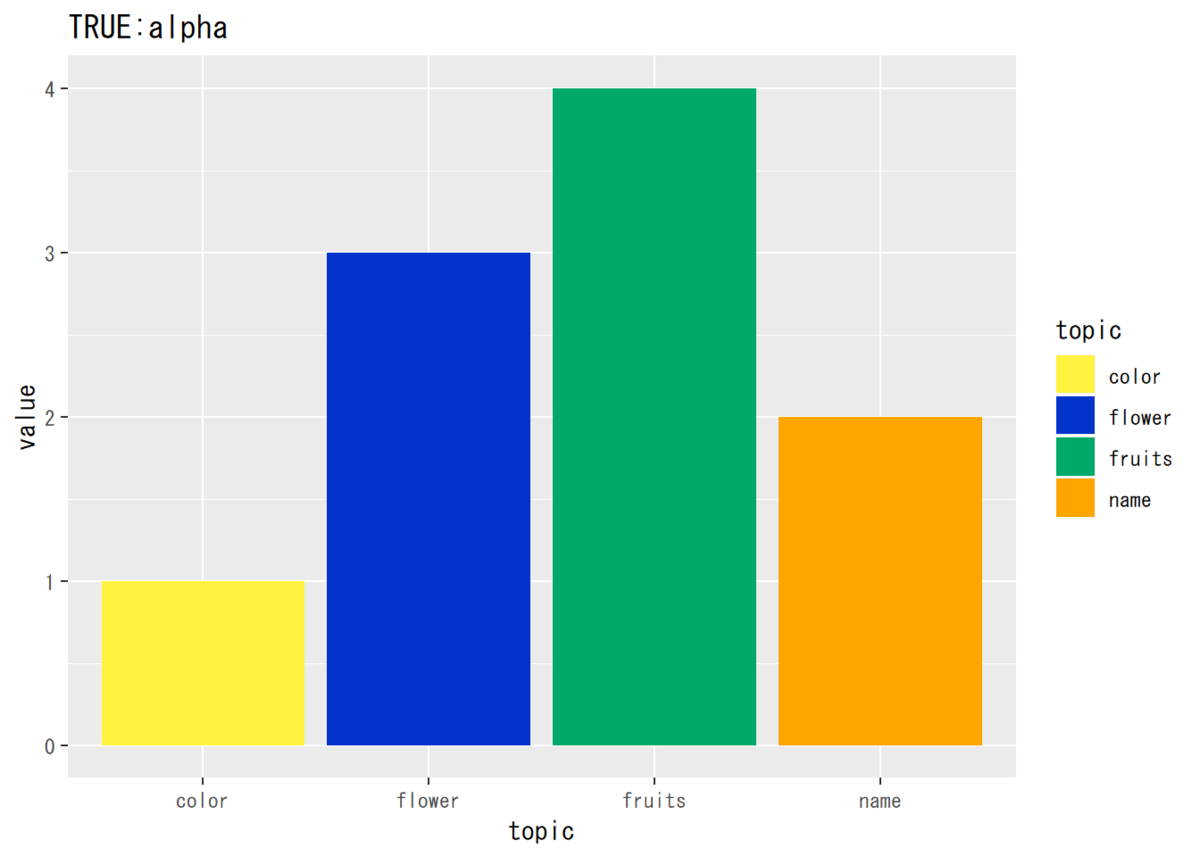
続いて、このハイパーパラメータ$\boldsymbol{\alpha}$を使ってトピック分布$\boldsymbol{\Theta}$を生成します。
# パラメータを生成 theta_dk_true <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), k_index)) for(d in 1:D) { theta_dk_true[d, ] <- MCMCpack::rdirichlet(n = 1, alpha = alpha_k_true) }
トピック分布はディリクレ分布に従って生成されるので、{MCMCpack}パッケージのrdirichlet()を使います。引数にn = 1を指定すると返ってくる値の総和が1になります。パラメータはalpha =に指定します。
これもグラフで確認しましょう。
## トピック分布のパラメータ # データフレームを作成 theta_true_df_wide <- cbind(as.data.frame(theta_dk_true), doc = as.factor(1:D)) theta_true_df_long <- pivot_longer( theta_true_df_wide, cols = -doc, names_to = "topic", values_to = "prob" ) # 作図 ggplot(theta_true_df_long, aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap(~ doc, labeller = label_both) + # グラフの分割 scale_fill_manual(values = c("#FFF33F", "#0233CB", "#00A968", "Orange")) + # 色 theme(axis.text.x = element_text(angle = 90)) + # x軸ラベルの角度 labs(title = "TRUE:Theta") # タイトル
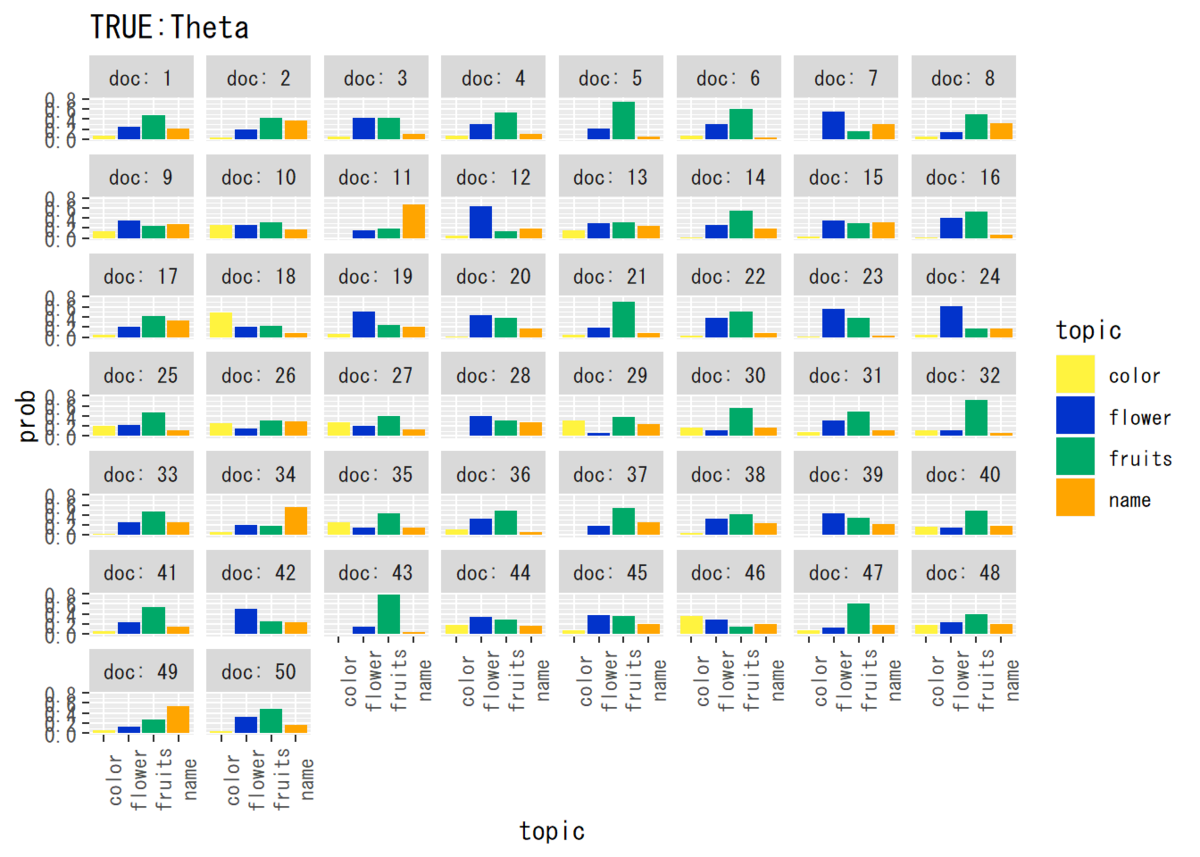
単語分布については最初に作成したものを用います。
単語集合の作成
では、パラメータが揃ったので単語集合を生成しましょう。
# 各単語のトピックの受け皿 z_dn_true <- matrix(0, nrow = D, ncol = N) # 単語集合の受け皿 N_dv <- matrix(0, nrow = D, ncol = V, dimnames = list(paste0("d=", 1:D), v_index)) for(d in 1:D) { for(n in 1:N) { # トピックを生成 tmp_z_dn <- rmultinom(n = 1, size = 1, prob = theta_dk_true[d, ]) z_dn_true[d, n] <- which(tmp_z_dn == 1) k <- z_dn_true[d, n] # 単語を生成 N_dv[d, ] <- N_dv[d, ] + rmultinom(n = 1, size = 1, prob = phi_kv_true[k, ]) } }
N_dv[1:6, 1:10] ## あお あか オレンジ しろ みどり もも ラベンダー レモン 黄緑 青緑 ## d=1 0 1 13 1 8 23 7 8 0 0 ## d=2 0 0 6 2 10 21 4 3 1 0 ## d=3 2 2 7 7 7 20 3 6 0 2 ## d=4 0 1 15 4 7 24 4 12 2 0 ## d=5 0 0 14 0 2 21 2 16 0 0 ## d=6 0 1 13 2 3 26 4 7 0 0
基本的な処理は混合ユニグラムモデルのときと同様です。
ただし、単語ごとにトピックを生成するため、トピック生成から単語の生成の処理を文書ごとに$N$回繰り返します。1語ずつ生成するためsize = 1となります。
各文書の語数N_dの値は同じなので、そのまま用います。
これで、推定に必要なパラメータ類は揃いました。では、各手法による推定結果と比較していきましょう。
推定
混合ユニグラムモデルのEMアルゴリズム
・トピック分布$\boldsymbol{\theta}$
・単語分布$\boldsymbol{\Phi}$
混合ユニグラムモデルの変分ベイズ推定
・トピック分布$\boldsymbol{\theta}$
・単語分布$\boldsymbol{\Phi}$
混合ユニグラムモデルのギブスサンプリング
上と同様の結果なため省略します。
PLSA
・トピック分布$\boldsymbol{\Theta}$
トピック分布:PLSA
・単語分布$\boldsymbol{\Phi}$
単語分布:PLSA
LDA
・トピック分布$\boldsymbol{\Theta}$
トピック分布:LDA
・単語分布$\boldsymbol{\Phi}$
単語分布:LDA
ギブスサンプリング
・トピック分布$\boldsymbol{\theta}$
トピック分布:LDA:ギブスサンプリング
・単語分布$\boldsymbol{\phi}$
単語分布:LDA:ギブスサンプリング
参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
現在、記事の内容を大幅に書き直しております。すみません。