はじめに
『ゼロからできるMCMC』の図とサンプルコードをR言語で再現します。本と一緒に読んでください。
この記事は、7.2節の内容です。2次元の正方格子のイジングモデルをメトロポリス法・ギブスサンプリング・Wolffのアルゴリズムを用いてシミュレーションします。
【前の章の内容】
飛ばした
【他の章の内容】
【この章の内容】
この節で利用するパッケージを読み込みます。
# 7.2節で利用するパッケージ library(tidyverse) library(gganimate)
gganimateは、gif画像を作成するパッケージです。シミュレーションの過程をアニメーションで確認するのに使います。
7.2.1 メトロポリス法
メトロポリス法を用いたイジングモデルを実装します。
・エネルギーの計算
まずは、スピン全体$\{s\}$のエネルギー$E(\{s\})$を計算する関数を作成しておきます。計算式は
です。ここで、$s_i$は$i$番目の格子上のスピンであり、$\langle i,j \rangle$は隣接するスピンの組を表します。
この資料で扱う2次元の正方格子の場合は
となります(たぶん)。ここで$i$番目のスピン$s_i$のy軸座標を$i_y$、x軸座標を$i_x$で表すことにします。$N$は1辺のスピン(あるいは格子点)の数で、スピンは全部で$N^2$個あります。
要するに、前の項は行方向に並ぶ2つのスピンの積と列方向に並ぶ2つのスピンの積の総和に$-J$を掛けたもので、後の項は全てのスピンの和に$-h$を掛けたものです。
この計算式を、(愚直に)関数として定義すると次のようになります。
# エネルギーの計算関数を作成:式(7.45) fn_E <- function(spin_mat, J = 1, h = 0) { # 1辺のスピン数を取得 N <- nrow(spin_mat) # 変数を初期化 sum_s_i <- 0 # 全てのスピンの和 sum_s_ij <- 0 # 隣接する全ての組み合わせのスピンの積の和 # 列インデックスを順番に生成 for(i_x in 1:N) { # 右隣のインデックスを取得 i_x_plus <- i_x + 1 # 行インデックスを順番に生成 for(i_y in 1:N) { # 下隣のインデックスを取得 i_y_plus <- i_y + 1 # i番目のスピンを加算 sum_s_i <- sum_s_i + spin_mat[i_y, i_x] # i番目と右隣のスピンとの積を加算 if(i_x < N) { # N列目のとき右隣はない sum_s_ij <- sum_s_ij + spin_mat[i_y, i_x] * spin_mat[i_y, i_x_plus] } # i番目と下隣のスピンとの積を加算 if(i_y < N) { # N行目のとき下隣はない sum_s_ij <- sum_s_ij + spin_mat[i_y, i_x] * spin_mat[i_y_plus, i_x] } } } # エネルギーを計算:式(7.45) energy <- - J * sum_s_ij - h * sum_s_i return(energy) }
次項では、もう少し処理効率がよくなるように定義します。(C++での実装例がこんな感じでした。)
ただしメトロポリス法においては、$k$回目の試行時のスピン$\{s^{(k)}\}$のエネルギー$E(\{s^{(k)}\})$と、$i$番目のスピン$s_{i_x,i_y}$を反転させたエネルギー$E(\{s'\})$との差
を求める際に、式(7.45)の計算を行います。
反転させたスピンを$s'_{i_y,i_x}$で表すことにすると、この式は、$i$番目に関する項以外は同じものなので打ち消されて
と整理できます。さらに$s'_{i_y, i_x} = - s_{i_y, i_x}$なので、置き換えると
となります。
よって$\Delta E$の計算式(7.50)を実装してシミュレーションすればいいのですが、少々アルゴリズムがシンプルになりすぎてしまいます。そこでメトロポリス法のアルゴリズムを明示的に実装するために、$i$番目のスピンに関するエネルギーの計算式
を関数定義して、シミュレーションに用いることにします。$\sum_{\pm 1} s_{i_y \pm 1, i_x} + s_{i_y, i_x \pm 1}$は、$s_{i_y-1, i_x} + s_{i_y+1, i_x} + s_{i_y, i_x-1} + s_{i_y, i_x+1}$のことです。
# エネルギーの計算関数を作成:式(7.49) fn_simpleE <- function(spin_mat, J = 1, h = 0) { # 1辺のスピン数を取得 N <- nrow(spin_mat) # 隣接する全ての組み合わせのスピンの積の和を初期化 sum_s_ij <- 0 # i番目と右隣のスピンとの積を加算 if(i_x < N) { # N列目のとき右隣はない sum_s_ij <- sum_s_ij + spin_mat[i_y, i_x] * spin_mat[i_y, i_x + 1] } # i番目と下隣のスピンとの積を加算 if(i_y < N) { # N行目のとき下隣はない sum_s_ij <- sum_s_ij + spin_mat[i_y, i_x] * spin_mat[i_y + 1, i_x] } # i番目と左隣のスピンとの積を加算 if(i_x > 1) { # N列目のとき左隣はない sum_s_ij <- sum_s_ij + spin_mat[i_y, i_x] * spin_mat[i_y, i_x - 1] } # i番目と上隣のスピンとの積を加算 if(i_y > 1) { # N行目のとき上隣はない sum_s_ij <- sum_s_ij + spin_mat[i_y, i_x] * spin_mat[i_y - 1, i_x] } # エネルギーを計算:式(7.45) energy <- - J * sum_s_ij - h * spin_mat[i_y, i_x] return(energy) }
この関数をfn_simpleE()としました。fn_simpleE()を、最初に作成した(あるいは次項で作成する)fn_E()にsそのまま置き換えてもシミュレーションできます。
ちなみに、本では周期境界条件を仮定していますが、(「有限体積の効果を減らすために」の意味がよく分からなかったので)この例では仮定していません(N行・列ごとに周期しているとした方が実装が楽な気はしました)。
・初期値の設定
続いて、一辺当たりのスピンの数$N$を設定して、スピンの初期値を生成します。
# 1辺のスピン数を指定 N <- 100 # スピンのマトリクスを初期化 spin_mat <- matrix(sample(x = c(-1, 1), size = N^2, replace = TRUE), nrow = N, ncol = N) # 確認 spin_mat[1:5, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 1 -1 -1 1 1 ## [2,] 1 1 1 -1 1 ## [3,] -1 1 -1 1 -1 ## [4,] 1 -1 1 1 1 ## [5,] -1 -1 1 1 1
$N^2$個の-1か1をランダムに生成して、$N \times N$のマトリクスを作成します。
これを作図用にデータフレームに格納します。
# 作図用にスピンのデータフレームを作成 spin_df <- tibble( i_y = rep(1:N, times = N), i_x = rep(1:N, each = N), spin = as.vector(spin_mat), label = as.factor(paste0("iter:", 0, ", rate:", sum(spin_mat) / N^2)) ) # 確認 head(spin_df)
## # A tibble: 6 x 4 ## i_y i_x spin label ## # A tibble: 6 x 4 ## i_y i_x spin label ## <int> <int> <dbl> <fct> ## 1 1 1 1 iter:0, rate:0.0102 ## 2 2 1 1 iter:0, rate:0.0102 ## 3 3 1 -1 iter:0, rate:0.0102 ## 4 4 1 1 iter:0, rate:0.0102 ## 5 5 1 -1 iter:0, rate:0.0102 ## 6 6 1 1 iter:0, rate:0.0102
$N^2$個のスピン(格子点)の座標の組み合わせを作成します。1からNの値をrep()で複製します。y軸の値は、times引数によって全体をN回繰り返すように複製します。x軸の値は、each引数によって要素ごとにN個に複製します。(expand.grid()という関数があるのをさっき知った、、、)
label列は、gif画像を作成するのに利用します。
このデータフレームを用いて作図します。
# 初期値を作図 ggplot(spin_df, aes(x = i_x, y = i_y, fill = spin)) + geom_tile() + # ヒートマップ scale_fill_gradient(low = "red", high = "yellow", breaks = c(-1, 1), guide = guide_legend()) + # タイルの色 coord_fixed(ratio = 1) + # アスペクト比 labs(subtitle = paste0("rate:", sum(spin_mat) / N^2))
geom_tile()でヒートマップを作成します。spin_matにおいてy軸番号($i_y = 1, \cdots, N$)は下方向に並んでいますが、ヒートマップにおいては上方向に並びます(aes()のy引数に-i_yを渡すと下方向に並べられます(ただしy軸の値が0から-Nになります))。

・メトロポリス法によるシミュレーション
パラメータを設定します。
# パラメータを指定 J <- 1 h <- 0 temperature <- 2
結合定数$J$をJ、外部磁場$h$をh、温度$T$をtemperatureとします。
$N^2$個のスピンごとを1試行とします。更新するスピンは、順番に決めることもランダムに決めることもできます。
スピンの総和$\sum_{i_y=1}^N \sum_{i_x=1}^N s_{i_y,i_x}$の絶対値とその最大値$N^2$との割合が指定した値を越えるまで繰り返します。ただし収束しない場合のため、最大試行回数を指定してその回数に達したらbreakで終了します。
# 最大試行回数を指定 max_iter <- 100 # 試行回数を初期化 iter <- 0 # メトロポリス法 while(abs(sum(spin_mat)) / N^2 < 0.9) { # 指定したレートに達するまで # 試行回数を加算 iter <- iter + 1 # 更新するスピン番号を生成 i_vec <- 1:N^2 # 順番に選択 #i_vec <- sample(1:N^2, size = N^2, replace = FALSE) # 順番をランダムに選択 #i_vec <- sample(1:N^2, size = N^2, replace = TRUE) # ランダムに選択 # 1試行における更新回数を初期化 n_accept <- 0 # 配位を更新 for(i in i_vec) { # スピンのインデックスを計算 i_y <- ifelse(i %% N == 0, yes = N, no = i %% N) # 行番号 i_x <- (i - 1) %/% N + 1 # 列番号 # エネルギーを計算:式(7.49) energy <- fn_simpleE(spin_mat, J, h) # i番目のスピンを反転させたマトリクスを作成 spin_dash_mat <- spin_mat spin_dash_mat[i_y, i_x] <- spin_dash_mat[i_y, i_x] * (-1) # エネルギーを計算:式(7.49) energy_dash <- fn_simpleE(spin_dash_mat, J, h) # 判定用の確率値を計算:式(4.46') prob <- exp((energy - energy_dash) / temperature) # テスト値を生成 metropolis <- runif(n = 1, min = 0, max = 1) # メトロポリステストにより配位を更新 if(prob > metropolis) { # スピンを更新 spin_mat <- spin_dash_mat # 更新回数を加算 n_accept <- n_accept + 1 } } # スピンのデータフレームを作成 tmp_spin_df <- tibble( i_y = rep(1:N, times= N), i_x = rep(1:N, each= N), spin = as.vector(spin_mat), label = as.factor(paste0( "J=", J, ", h=", h, ", T=", temperature, ", iter:", iter, ", rate:", sum(spin_mat) / N^2 )) ) # 結果を結合 spin_df <- rbind(spin_df, tmp_spin_df) # 途中経過を表示 #print(paste0("iter:", iter, ", accept:", n_accept, ", rate:", sum(spin_mat) / N^2)) # 最大回数に達したら終了 if(iter == max_iter) break }
まずは、スピン番号$i$から座標$i_y, i_x$に変換します(もっといい方法があれば教えて下さい)。
1から$N^2$番目までのスピンを順番に更新する場合は、spin_matの1列目の要素を1行目からN行まで更新し、次に2列目の要素を1からN行と更新していきます。
続いて、現在のスピンspin_matのエネルギーをfn_simpleE()で計算して、energyとします。
spin_matのコピーをspin_dash_matとし、$i$番目のスピンspin_dash_mat[i_y, i_x]に-1を掛けて反転させます。同様にエネルギーを計算してenergy_dashとします。
最後に、$\exp(- \beta \Delta E)$の計算によって求めた確率値(として解釈できる値)pが、0から1の一様乱数metropolisよりも大きいとき、スピンspin_matを、反転させたスピンspin_dash_matに更新します。
更新前のスピンspin_matは$\{s^{(k)}\}$、spin_dash_matは$\{s'\}$、更新後のスピンspin_matは$\{s^{(k+1)}\}$に対応します。更新されなかった(条件を満たさなかった)場合もspin_matをそのまま$\{s^{(k+1)}\}$として次の試行を行います。
・結果の確認
最終結果を作図します。
# 最終結果を作図 ggplot(tmp_spin_df, aes(x = i_x, y = i_y, fill = spin)) + geom_tile() + # ヒートマップ scale_fill_gradient(low = "red", high = "yellow", breaks = c(-1, 1), guide = guide_legend()) + # タイルの色 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Metropolis Method", subtitle = paste0("J=", J, ", h=", h, ", T=", temperature, ", iter:", iter, ", rate:", sum(spin_mat) / N^2))
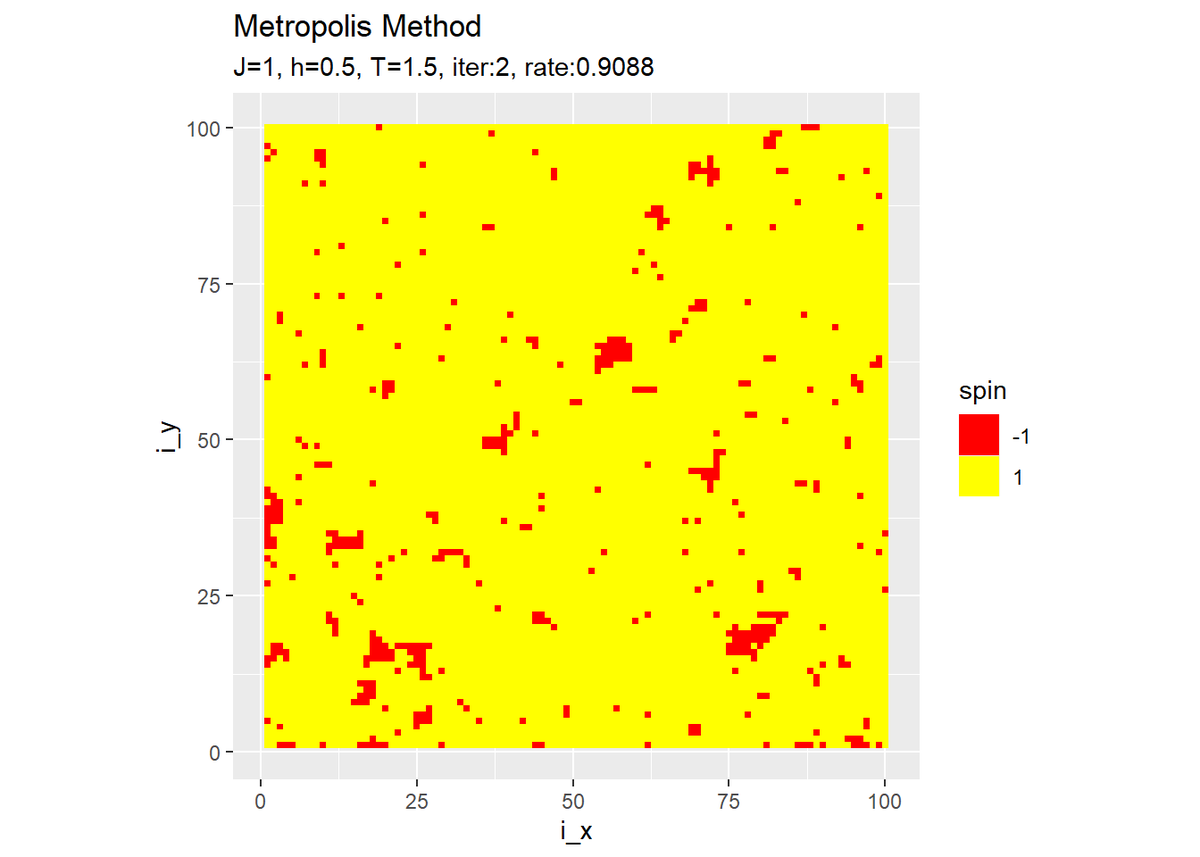
パラメータによって変化の仕方が異なります。
・アニメーションの作成
シミュレーションの推移をアニメーション(gif画像)で確認するためのコードです。
# アニメーション用のグラフを作成 graph <- ggplot(spin_df, aes(x = i_x, y = i_y, fill = spin)) + geom_tile() + # ヒートマップ scale_fill_gradient(low = "red", high = "yellow", breaks = c(-1, 1), guide = guide_legend()) + # タイルの色 coord_fixed(ratio = 1) + # アスペクト比 gganimate::transition_manual(label) + # フレーム labs(title = "Metropolis Method", subtitle = "{current_frame}") # gif画像を出力 gganimate::animate(graph, nframes = iter + 1, fps = 10)
表示する順番を示す列をgganimate::transition_manual()に指定します。
初期値を含むためフレーム数nframesはiter+1です。
他のアルゴリズムの結果もこのコードでgif画像に変換できます。
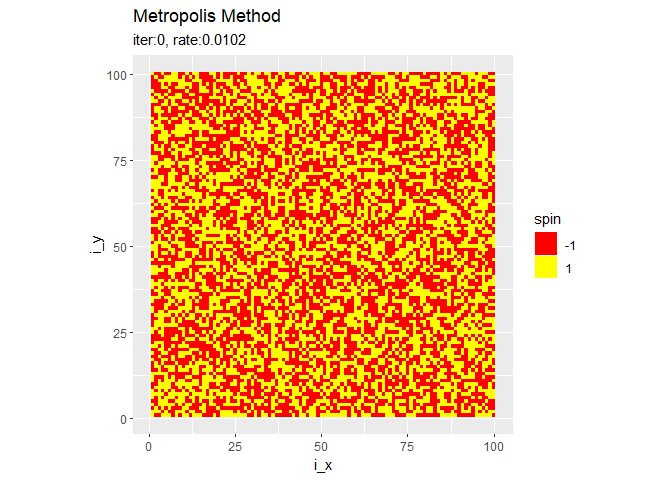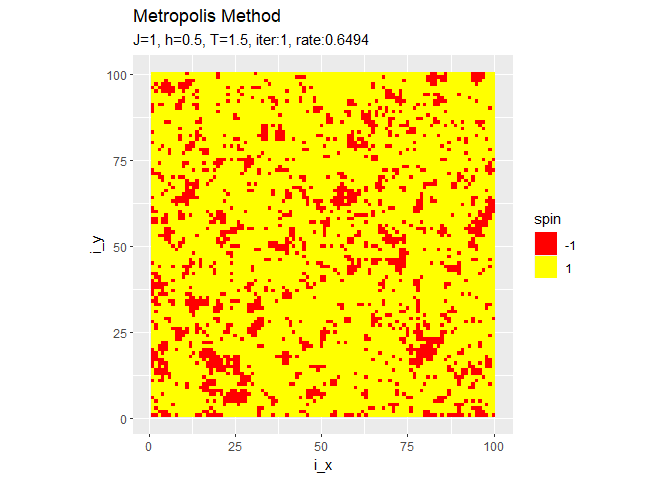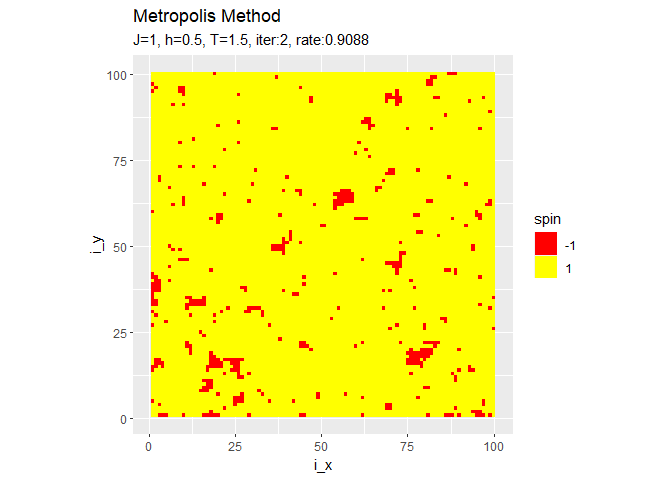
・他のパラメータでのシミュレーション

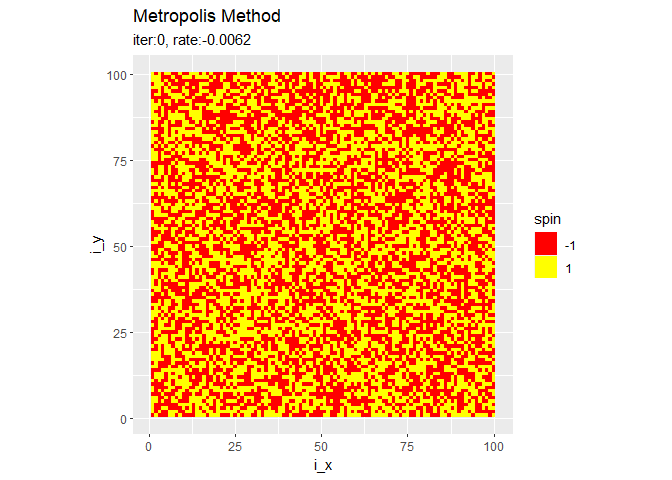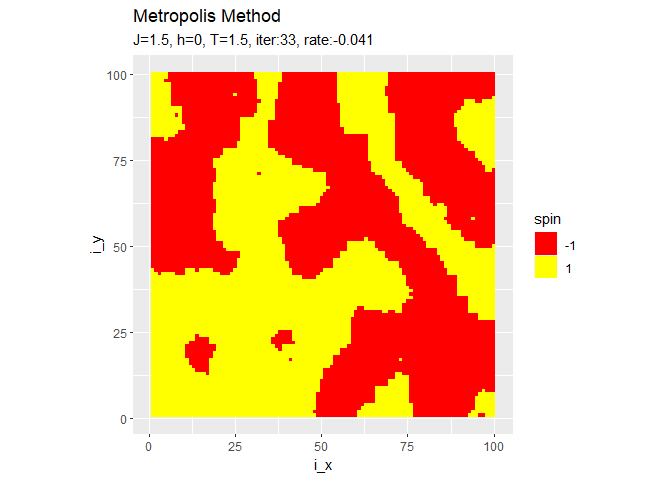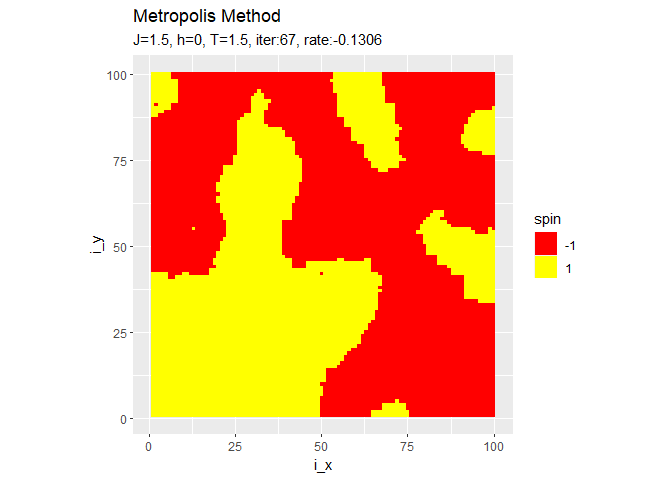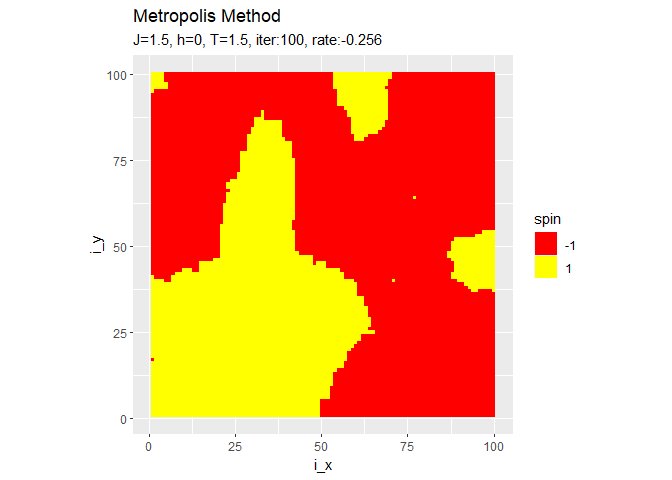
$h$に従ってスピンが上下どちらの向きに揃うのかが決まります。$h = 0$のときはランダムに決まります。右の結果は、更新するスピンの順番をランダムに選んだものです。
パラメータによっては、収束しないこともあります。
・収束後の変化
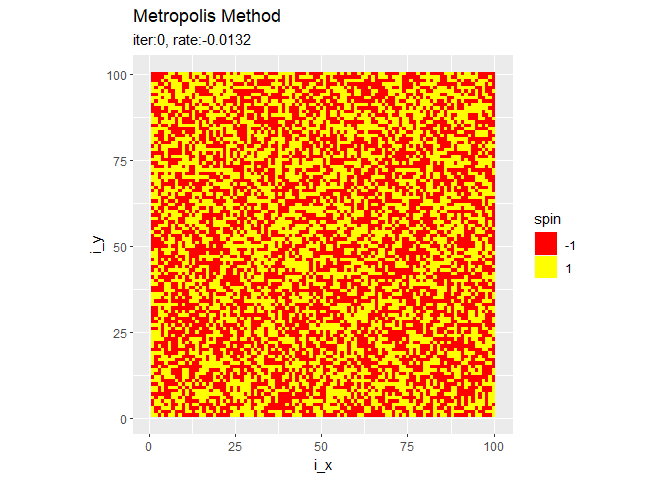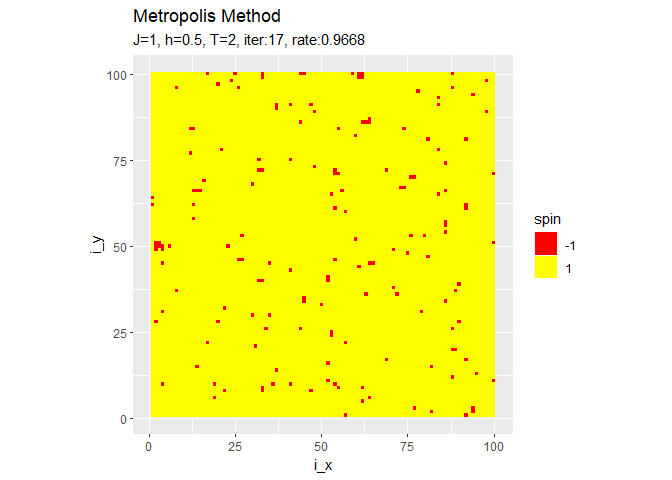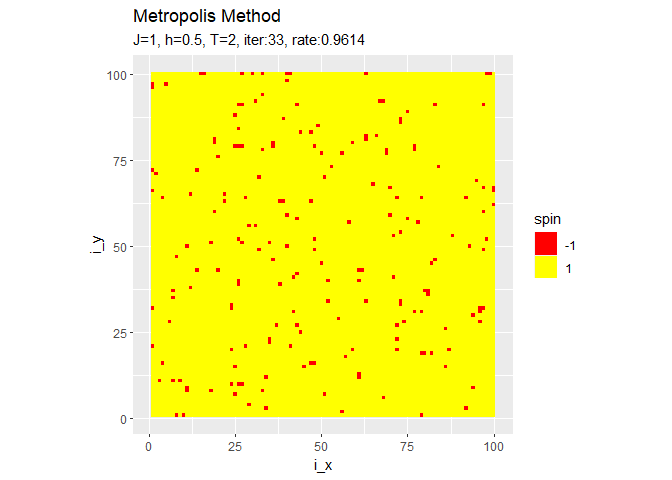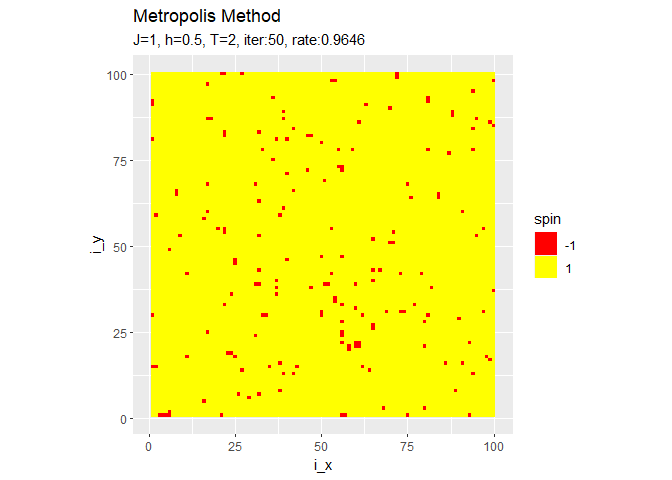
ちなみに収束後も続けるとこんな感じになります。
7.2.2 ギブスサンプリング
ギブスサンプリングを用いたイジングモデルを実装します。
・エネルギーの計算
まずは、エネルギーの計算式(7.45)を関数として定義しておきます。
# エネルギーの計算関数を作成:式(7.45) fn_E <- function(spin_mat, J = 1, h = 0) { # 1辺のスピン数を取得 N <- nrow(spin_mat) # 全てのスピンの和 sum_s_i <- sum(spin_mat) # 右隣のスピンとの積の和 sum_s_ij_x <- sum(spin_mat[, -N] * spin_mat[, -1]) # 下隣のスピンとの積の和 sum_s_ij_y <- sum(spin_mat[-1, ] * spin_mat[-N, ]) # エネルギーを計算:式(7.45) energy <- - J * (sum_s_ij_x + sum_s_ij_y) - h * sum_s_i return(energy) }
列方向に並ぶ2つのスピンの積$s_{i_y,i_x} s_{i_y,i_x+1}$は、N列目を除くspin_mat[, -N]と1列目を除くspin_mat[, -1]の積で一度に計算できます。同様に行方向に並ぶ2つのスピンの積$s_{i_y,i_x} s_{i_y+1,i_x}$は、1行目を除くspin_mat[-1, ]とN行目を除くspin_mat[-N, ]の積です。この2つ計算結果の総和が式(7.45)の$\sum_{\langle i,j \rangle} s_i s_j$に対応します。
(周期境界条件を置く場合は、spin_mat * spin_mat[, c(2:N, 1)]、spin_mat * spin_mat[c(2:N, 1), ]で計算できます。)
・初期値の設定
前項と同様にして、スピンの初期化します。
・ギブスサンプリングによるシミュレーション
パラメータを指定して、シミュレーションを行います。
# パラメータを指定 J <- 1 h <- 0 temperature <- 2 # 最大試行回数を指定 max_iter <- 100 # 試行回数を初期化 iter <- 0 # ギブスサンプリング while(abs(sum(spin_mat)) / N^2 < 0.9) { # 指定したレートに達するまで # 試行回数を加算 iter <- iter + 1 # 更新するスピン番号を生成 i_vec <- 1:N^2 # 順番に選択 #i_vec <- sample(1:N^2, size = N^2, replace = FALSE) # 順番をランダムに選択 #i_vec <- sample(1:N^2, size = N^2, replace = TRUE) # ランダムに選択 # 配位を更新 for(i in i_vec) { # スピンのインデックスを計算 i_y <- ifelse(i %% N == 0, yes = N, no = i %% N) # 行番号 i_x <- (i - 1) %/% N + 1 # 列番号 # i番目のスピンを反転させたマトリクスを作成 spin_plus_mat <- spin_mat spin_plus_mat[i_y, i_x] <- 1 spin_minus_mat <- spin_mat spin_minus_mat[i_y, i_x] <- -1 # エネルギーを計算:式(7.45)と式(7.46)の分子の指数部分 energy_plus <- - fn_E(spin_plus_mat, J, h) / temperature energy_minus <- - fn_E(spin_minus_mat, J, h) / temperature # エネルギーの指数を計算:式(7.46)の分子 if(max(energy_plus, energy_minus) > 700) { # 最大値を取得 max_energy <- max(energy_plus, energy_minus) # オーバーフロー対策 exp_energy_plus <- exp(energy_plus - max_energy) exp_energy_minus <- exp(energy_minus - max_energy) } else if(min(energy_plus, energy_minus) < - 700) { # 最小値を取得 min_energy <- min(energy_plus, energy_minus) # アンダーフロー対策 exp_energy_plus <- exp(energy_plus - min_energy) exp_energy_minus <- exp(energy_minus - min_energy) } else { exp_energy_plus <- exp(energy_plus) exp_energy_minus <- exp(energy_minus) } # 確率を計算:式(7.46) p_plus <- exp_energy_plus / (exp_energy_plus + exp_energy_minus) p_minus <- exp_energy_minus / (exp_energy_plus + exp_energy_minus) # 確率に従いスピンを更新 spin_mat[i_y, i_x] <- sample(c(-1, 1), size = 1, prob = c(p_minus, p_plus)) } # スピンのデータフレームを作成 tmp_spin_df <- tibble( i_y = rep(1:N, each = N), i_x = rep(1:N, times = N), spin = as.vector(spin_mat), label = as.factor(paste0( "J=", J, ", h=", h, ", T=", temperature, ", iter:", iter, ", rate:", sum(spin_mat) / N^2 )) ) # 結果を結合 spin_df <- rbind(spin_df, tmp_spin_df) # 途中経過を表示 #print(paste0("iter:", iter, ", rate:", sum(spin_mat) / N^2)) # 最大回数に達したら終了 if(iter == max_iter) break }
$i$番目の要素(スピン)$s_{i_y,i_x}$を-1にしたものと1にした2つのマトリクスを作成します。
それぞれ$- \beta E(\{s\})$の計算をします。(次のオーバー(アンダー)フロー対策のため、エネルギー$E(\{s\})$ではなく指数をとる手前まで計算しておきます。)
exp()に関して、700ちょっと(-700ちょっと)でInf(0)になってしまいました。そこでenergy_plus, energy_minusの値によって、オーバーフロー(アンダーフロー)対策として最大値(最小値)を引いてから$\exp(- \beta E(\{s^{(\pm)}\}))$の計算をしています。
最後に、$i$番目のスピンの値を、確率p_plusで1、確率p_minusで-1として確率的に更新します。p_plus, p_minusはそれぞれ
で計算します。分母は、分配関数$Z = \exp(- \beta E(\{s^{(+)}\})) + \exp(- \beta E(\{s^{(-)}\}))$に対応しており、総和が1になるように正規化しています。
・結果の確認
# 最終結果を作図 ggplot(tmp_spin_df, aes(x = i_x, y = i_y, fill = spin)) + geom_tile() + # ヒートマップ scale_fill_gradient(low = "red", high = "yellow", breaks = c(-1, 1), guide = guide_legend()) + # タイルの色 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Gibbs Sampling", subtitle = paste0("J=", J, ", h=", h, ", T=", temperature, ", iter:", iter, ", rate:", sum(spin_mat) / N^2))
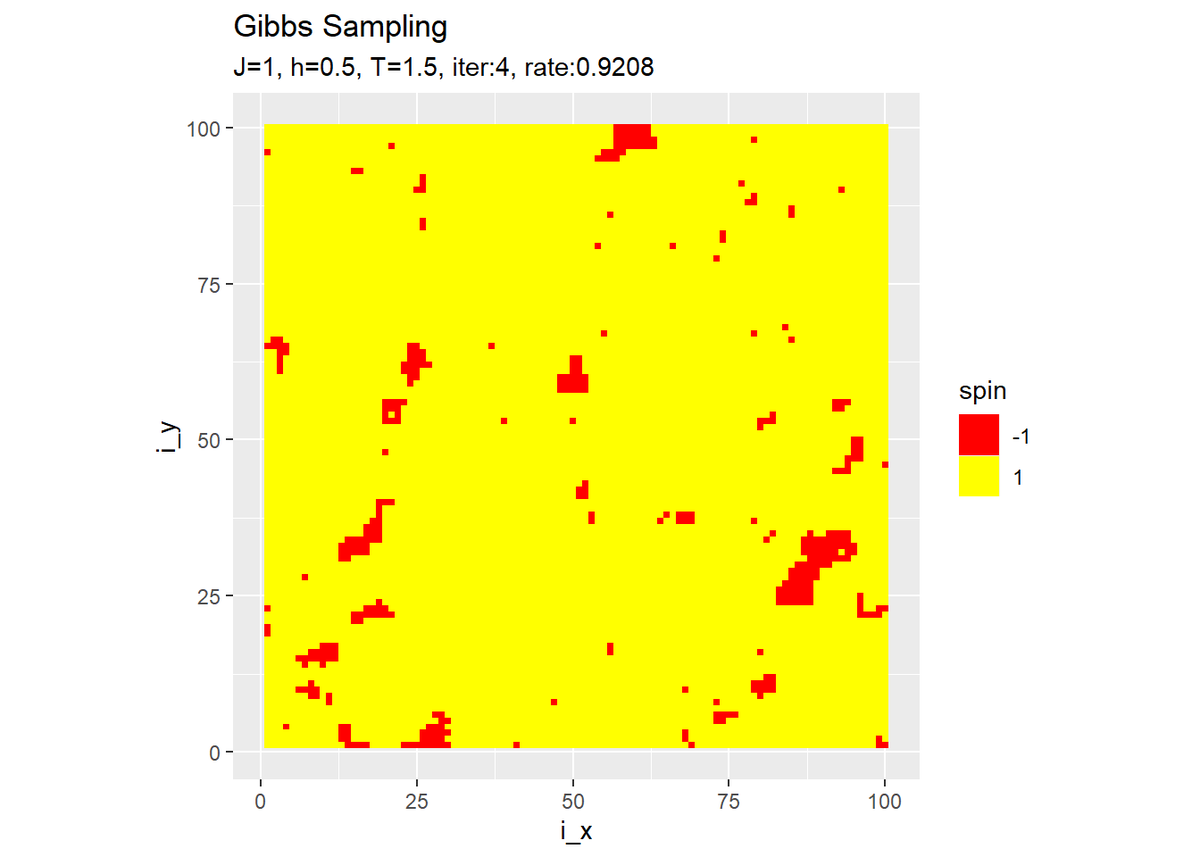
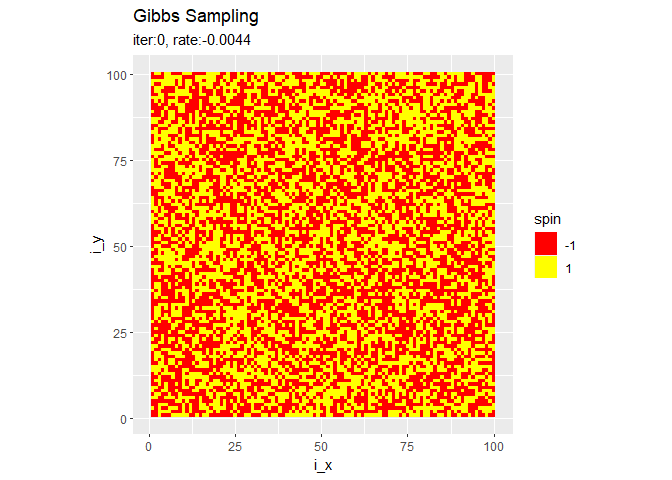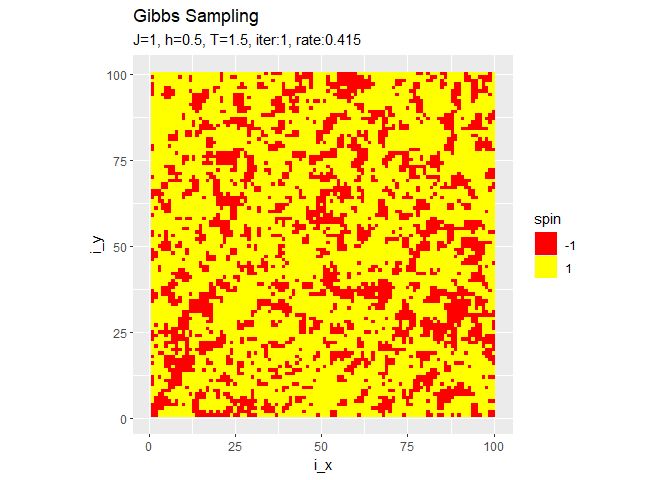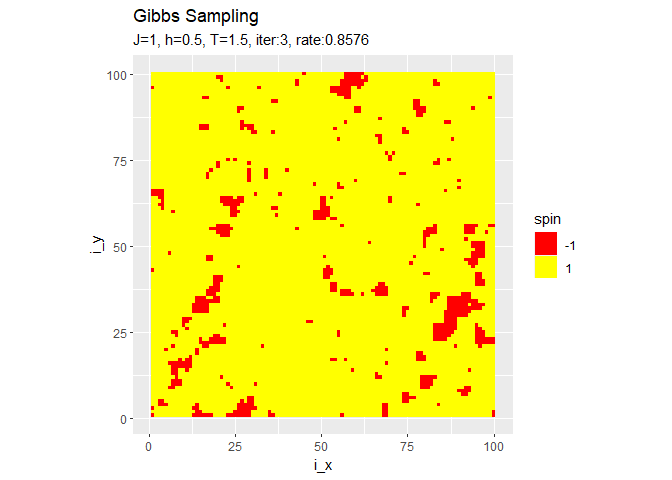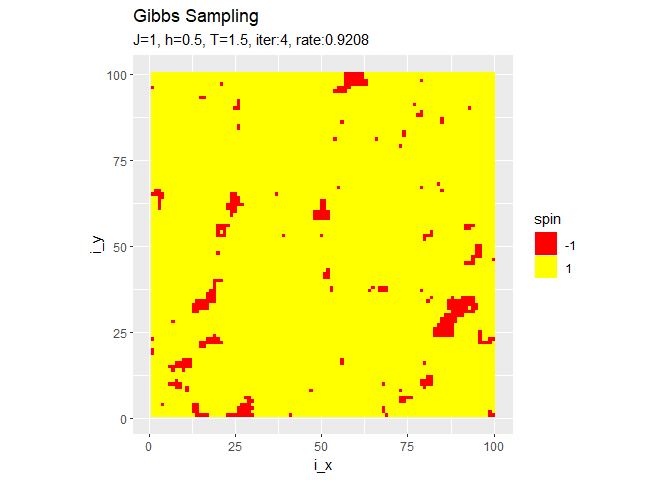
・他のパラメータでのシミュレーション


右の結果は、更新するスピンの順番をランダムに選んだものです。
・収束後の変化
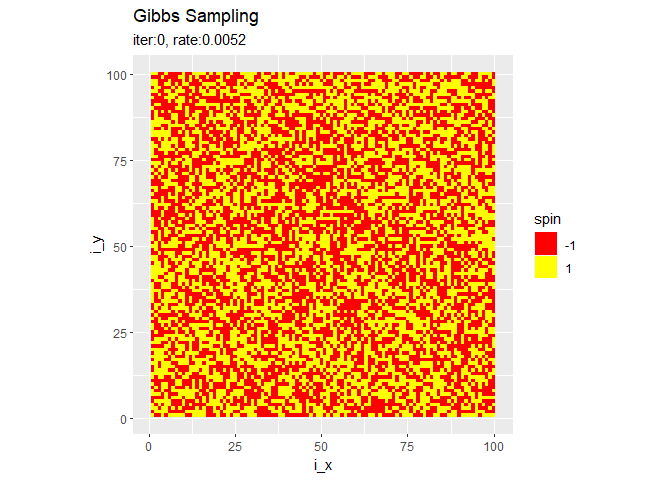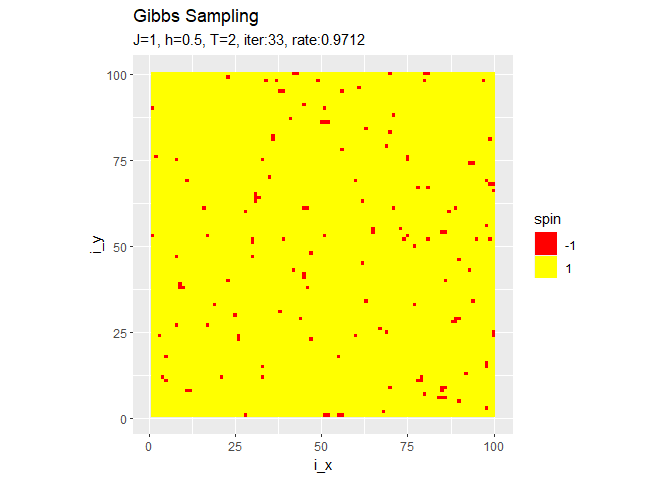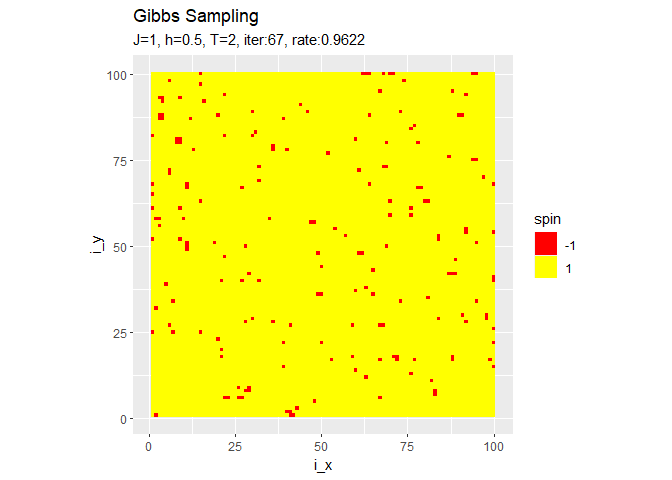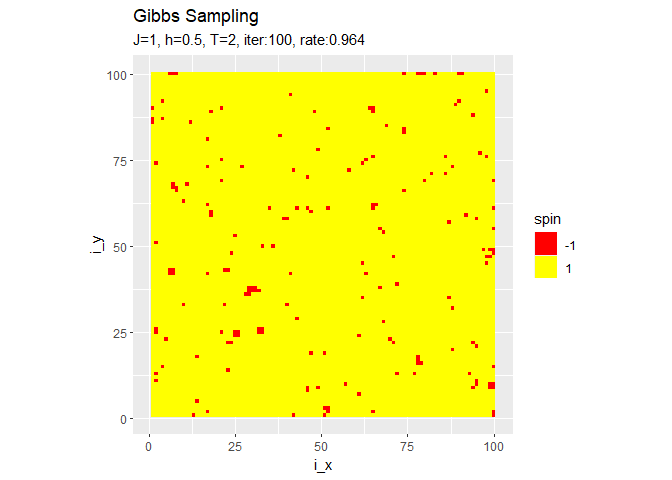
7.2.5 Wolffのアルゴリズム
Wolffアルゴリズムを用いたイジングモデルを実装します。
・初期値の設定
これまでと同様にして、スピンの初期化します。

・Wolffアルゴリズムによるシミュレーション
パラメータを設定して、隣接するスピンをクラスターに含めるかの判定に用いる確率値を計算します。
# パラメータを指定 J <- 1 h <- 0.5 temperature <- 2 # クラスタの追加判定用の確率値を計算 prob <- 1 - exp(-2 * J / temperature) prob
## [1] 0.7364029
確率値は、$1 - \exp(-2\frac{J}{T})$で計算します。
シミュレーションを行います。
# 最大試行回数を指定 max_iter <- 100 # 試行回数を初期化 iter <- 0 # Wolffアルゴリズム while(abs(sum(spin_mat)) / N^2 < 0.95) { # 指定したレートに達するまで # 試行回数を加算 iter <- iter + 1 # クラスタのマトリクスを初期化 cluster_mat <- matrix(1, nrow = N, ncol = N) # クラスタの起点となるスピンのインデックスを生成 i_y <- sample(x = 1:N, size = 1) i_x <- sample(x = 1:N, size = 1) # 起点のクラスタを設定 cluster_mat[i_y, i_x] <- 0 # 起点のクラスタのスピンを取得 spin_cluster <- spin_mat[i_y, i_x] # クラスタのインデックスを記録 cluster_idx_mat <- matrix(c(i_y, i_x), nrow = 1, ncol = 2) # クラスタ数を初期化 n_cluster <- 1 # 処理済みのクラスタ数を初期化 k <- 0 # 配位を更新 while(k < n_cluster) { # 処理済みのクラスタ数を加算 k <- k + 1 # クラスタのインデックスを取得 i_y <- cluster_idx_mat[k, 1] i_x <- cluster_idx_mat[k, 2] # 隣接するインデックスを計算 i_y_plus <- i_y + 1 i_x_plus <- i_x + 1 i_y_minus <- i_y - 1 i_x_minus <- i_x - 1 # 上隣を処理 if(i_y_minus >= 1) { # 枠内である if(spin_mat[i_y_minus, i_x] == spin_cluster) { # 現クラスタと同じスピンである if(cluster_mat[i_y_minus, i_x] == 1) { # 未処理である # 判定用の確率値を生成 r <- runif(n = 1, min = 0, max = 1) if(prob > r) { # 確率で判定 # クラスタを追加 cluster_mat[i_y_minus, i_x] <- 0 # 新たなクラスタのインデックスを記録 cluster_idx_mat <- rbind(cluster_idx_mat, c(i_y_minus, i_x)) # クラスタ数を加算 n_cluster <- n_cluster + 1 } } } } # 下隣を処理 if(i_y_plus <= N) { # 枠内である if(spin_mat[i_y_plus, i_x] == spin_cluster) { # 現クラスタと同じスピンである if(cluster_mat[i_y_plus, i_x] == 1) { # 未処理である # 判定用の確率値を生成 r <- runif(n = 1, min = 0, max = 1) if(prob > r) { # 確率で判定 # クラスタを追加 cluster_mat[i_y_plus, i_x] <- 0 # 新たなクラスタのインデックスを記録 cluster_idx_mat <- rbind(cluster_idx_mat, c(i_y_plus, i_x)) # クラスタ数を加算 n_cluster <- n_cluster + 1 } } } } # 左隣を処理 if(i_x_minus >= 1) { # 枠内である if(spin_mat[i_y, i_x_minus] == spin_cluster) { # 現クラスタと同じスピンである if(cluster_mat[i_y, i_x_minus] == 1) { # 未処理である r <- runif(n = 1, min = 0, max = 1) if(prob > r) { # 確率で判定 # クラスタを追加 cluster_mat[i_y, i_x_minus] <- 0 # 新たなクラスタのインデックスを記録 cluster_idx_mat <- rbind(cluster_idx_mat, c(i_y, i_x_minus)) # クラスタ数を加算 n_cluster <- n_cluster + 1 } } } } # 右隣を処理 if(i_x_plus <= N) { # 枠内である if(spin_mat[i_y, i_x_plus] == spin_cluster) { # 現クラスタと同じスピンである if(cluster_mat[i_y, i_x_plus] == 1) { # 未処理である # 判定用の確率値を生成 r <- runif(n = 1, min = 0, max = 1) if(prob > r) { # 確率で判定 # クラスタを追加 cluster_mat[i_y, i_x_plus] <- 0 # 新たなクラスタのインデックスを記録 cluster_idx_mat <- rbind(cluster_idx_mat, c(i_y, i_x_plus)) # クラスタ数を加算 n_cluster <- n_cluster + 1 } } } } } # クラスタのスピンを反転 spin_mat[cluster_mat == 0] <- spin_cluster * (-1) # スピンのデータフレームを作成 tmp_spin_df <- tibble( i_y = rep(1:N, each = N), i_x = rep(1:N, times = N), spin = as.vector(spin_mat), label = as.factor(paste0( "J=", J, ", h=", h, ", T=", temperature, ", iter:", iter, ", rate:", sum(spin_mat) / N^2 )) ) # 結果を結合 spin_df <- rbind(spin_df, tmp_spin_df) # 結果を表示 #print(paste0("iter:", iter, ", cluster:", k, ", rate:", sum(spin_mat) / N^2)) # 最大回数に達したら終了 if(iter == max_iter) break }
(かなり愚直に処理する実装になってしまいました。メインループの4つの処理を関数化したかったのですが、条件式と返り値が多くて思いつきませんでした。)
クラスタに含まれている各スピン$s_{i_y,i_x}$に関して、その上下左右のスピン$s_{i_y-1,i_x}, s_{i_y+1,i_x} , s_{i_y,i_x-1}, s_{i_y,i_x+1}$もクラスタに含めるかどうかを確率的に決めていきます。
各スピンがクラスタに含まれているかどうかをcluster_matで管理します。cluster_matの要素はspin_matに対応しており、各スピンがクラスタに含まれていれば0、含まれていなければ1とします。
初期値は全て1で、スピンがクラスタとして選ばれるたびに値を0に置き換えます。
スピンがクラスタに選ばれると、選ばれたスピンのインデックスをcluster_idx_matに行方向に結合していきます。
またクラスタ数をn_clusterとしてカウントします。
隣接するスピンをクラスタに加えるかを、条件式で判定します。
この例では周期境界条件をおいていないので、隣接するスピンが存在するかを調べます。
隣接するスピンが対象とのスピンと同じ値(向き)である必要があります。
既にクラスタに含まれている場合は処理を止めます。
3つの条件を満たす場合に、0から1の一様乱数を生成します。この乱数rをよりもパラメータから求めた確率probが大きいとき、隣接するスピンをクラスタに加えます。
現在対象としているスピンに関する処理が終わると、cluster_idx_matから次のスピンのインデックスを受け取り同じ作業を行います。
処理済みのクラスタ数kがn_clusterに達すれば、クラスタの追加作業が完了です。クラスタに含まれた全てのスピンを反転させて、1回の試行を終了します。
・結果の確認
# 最終結果を作図 ggplot(tmp_spin_df, aes(x = i_x, y = i_y, fill = spin)) + geom_tile() + # ヒートマップ scale_fill_gradient(low = "red", high = "yellow", breaks = c(-1, 1), guide = guide_legend()) + # タイルの色 coord_fixed(ratio = 1) + # アスペクト比 labs(title = "Wolff Algorithm", subtitle = paste0("J=", J, ", h=", h, ", T=", temperature, ", iter:", iter, ", rate:", sum(spin_mat) / N^2))
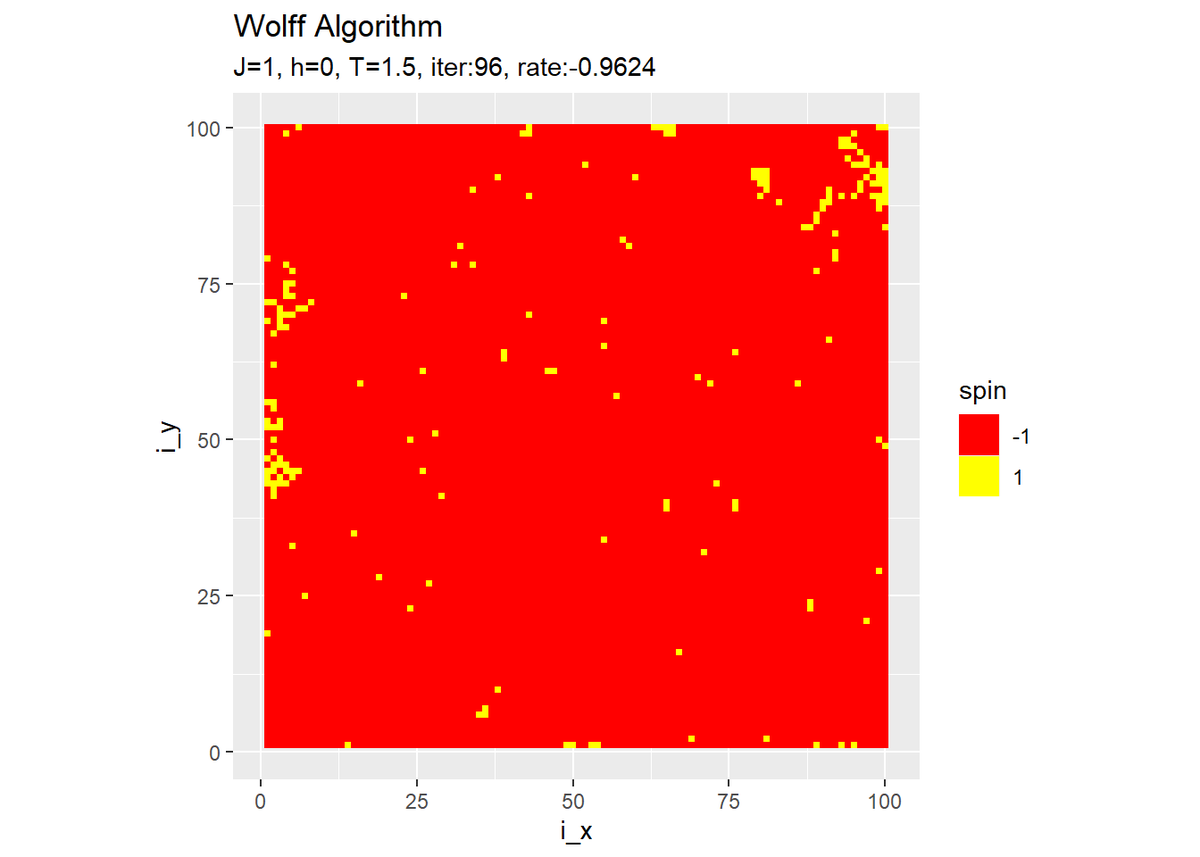

・他のパラメータでのシミュレーション


右の結果は、更新するスピンの順番をランダムに選んだものです。
・収束後の変化
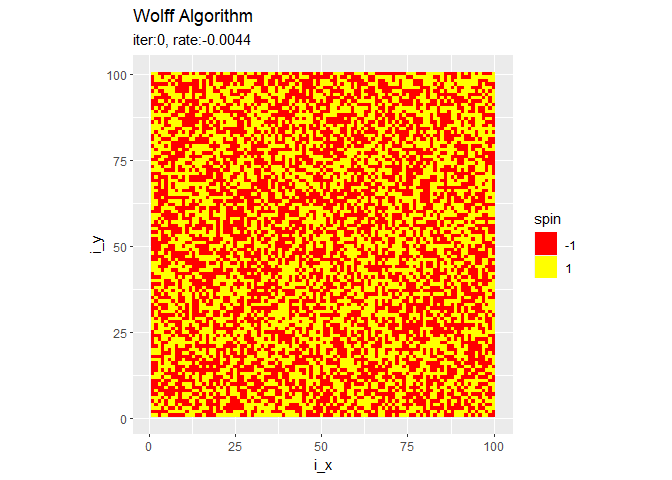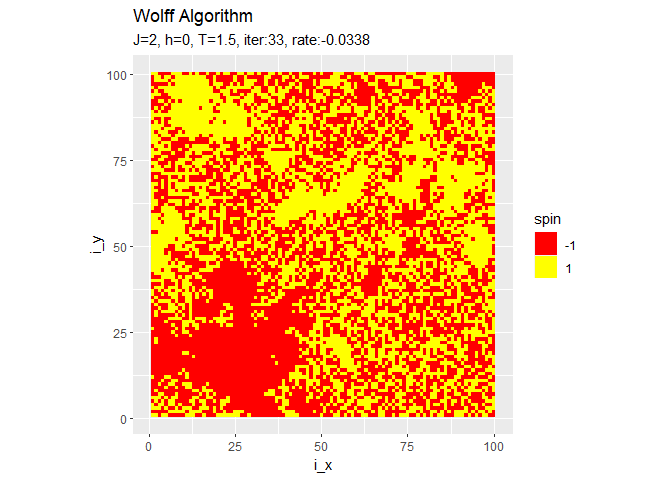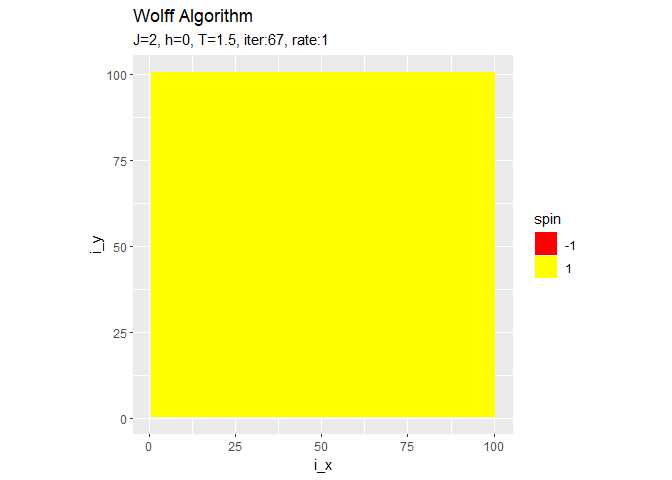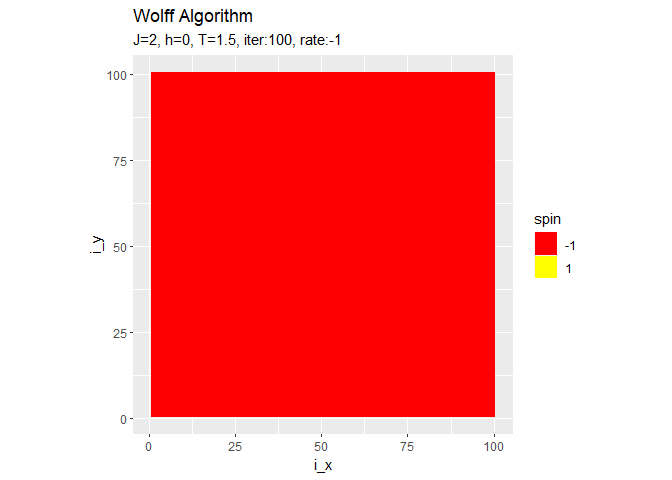
反転を続けるようです。
参考文献
おわりに
面白そうだったので、6章を飛ばしてこれを先にやってみました。しかしやっぱり物理学にまで手を広げる気はないなぁ。
ここまで来てようやく雰囲気を掴めた気がします。メトロポリス法は、更新前後の状態を基にした確率に従って更新される。ギブスサンプリングは、とり得る各状態を基にした確率に従って更新される。という理解でいいのかな。Wolffアルゴリズムは、イジングモデルにおける効率的な処理方法ですね。
はいっ!3月6日は、Berryz工房・カントリーガールズ・Buono!の元メンバー嗣永桃子さんのお誕生日です♪
私はBuono!が特に好きなのですが、ハマったのが解散2か月後でした、、、あぁ一度でいいからライブに参加したい。
【次の節の内容】
つづくはず
