はじめに

　『トピックモデル』(MLPシリーズ)の勉強会資料のまとめです。各種モデルやアルゴリズムを「数式」と「プログラム」を用いて解説します。
　本の補助として読んでください。

　この記事では、ユニグラムモデルにおけるMAP推定(ハイパーパラメータ推定)をR言語でスクラッチ実装します。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

はじめに
2.7 ユニグラムモデルのMAP推定の実装：ハイパーパラメータ推定
参考書籍
おわりに

2.7 ユニグラムモデルのMAP推定の実装：ハイパーパラメータ推定

　ユニグラムモデル(unigram model)に対する不動点反復法(固定点反復法・fixed point iteration)を用いた最大事後確率推定(MAP推定・maximum a posteriori estimation)を実装する。この節では、ハイパーパラメータに事前分布を設定して、ハイパーパラメータを推定する。
　ユニグラムモデルの定義や記号については「2.2：ユニグラムモデルの生成モデルの導出【青トピックモデルのノート】 - からっぽのしょこ」、パラメータの計算式については「2.7：ユニグラムモデルのMAP推定の導出：ハイパーパラメータ推定【青トピックモデルのノート】 - からっぽのしょこ」、ハイパーパラメータに事前分布を設定しない(パラメータを推定する)場合については「パラメータ推定」を参照のこと。

　利用するパッケージを読み込む。

# 利用パッケージ
library(tidyverse)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要である。ただし、作図コードについてはパッケージ名を省略するので、ggplot2 を読み込む必要がある。
　また、ネイティブパイプ演算子 |> を使う。magrittrパッケージのパイプ演算子 %>% に置き換えられるが、その場合は magrittr を読み込む必要がある。

文書データの簡易生成

　まずは、ユニグラムモデルの生成モデルに従って、bag-of-words表現の文書データ(語彙頻度データ)を生成する。
　トイデータの作成については「生成モデルの実装」を参照のこと。

　真の分布などの本来は得られない情報についてはオブジェクト名に true を付けて表す。

途中式の途中式(クリックで展開)

　パラメータ類を設定して、文書データを作成する。

# 文書数を指定
D <- 10

# 語彙数を指定
V <- 6

# 単語分布のハイパーパラメータを指定
true_beta   <- 1
true_beta_v <- rep(true_beta, times = V)

# 単語分布のパラメータを生成
#true_phi_v <- rep(1/V, times = V) # 一様パラメータの場合
true_phi_v <- MCMCpack::rdirichlet(n = 1, alpha = true_beta_v) |> # 多様パラメータの場合
  as.vector()

# 各文書の単語数を生成
N_d <- sample(x = 10:20, size = D) # 下限・上限を指定

# 文書データを生成
N_dv <- matrix(NA, nrow = D, ncol = V)
for(d in 1:D) { 
  
  # 各語彙の出現回数を生成
  N_dv[d, ] <- rmultinom(n = 1, size = N_d[d], prob = true_phi_v) |> # (多項乱数)
    as.vector()
  
  # 途中経過を表示
  print(paste0("document: ", d, ", words: ", N_d[d]))
}

[1] "document: 1, words: 10"
[1] "document: 2, words: 14"
[1] "document: 3, words: 15"
[1] "document: 4, words: 16"
[1] "document: 5, words: 19"
[1] "document: 6, words: 18"
[1] "document: 7, words: 17"
[1] "document: 8, words: 20"
[1] "document: 9, words: 11"
[1] "document: 10, words: 12"

　文書数 $D$ 、語彙数 $V$ 、単語分布(カテゴリ分布)の真のハイパーパラメータ $\beta^{\mathrm{truth}} \gt 0$ を指定して、真のパラメータ $\boldsymbol{\phi}^{\mathrm{truth}}$ を生成する。
　文書ごとに単語数 $N_d$ を決めて、多項分布の乱数により各語彙の出現回数 $N_{dv}$ を生成する。

　文書データを確認する。

# 観測データを確認
N_dv[1:5, ]; N_d[1:10]

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    2    0    4    2    1    1
[2,]    3    1    8    1    0    1
[3,]    1    2    4    2    2    4
[4,]    3    2    8    1    1    1
[5,]    2    0   11    3    0    3
 [1] 10 14 15 16 19 18 17 20 11 12

　文書ごとの語彙頻度をグラフで確認する。

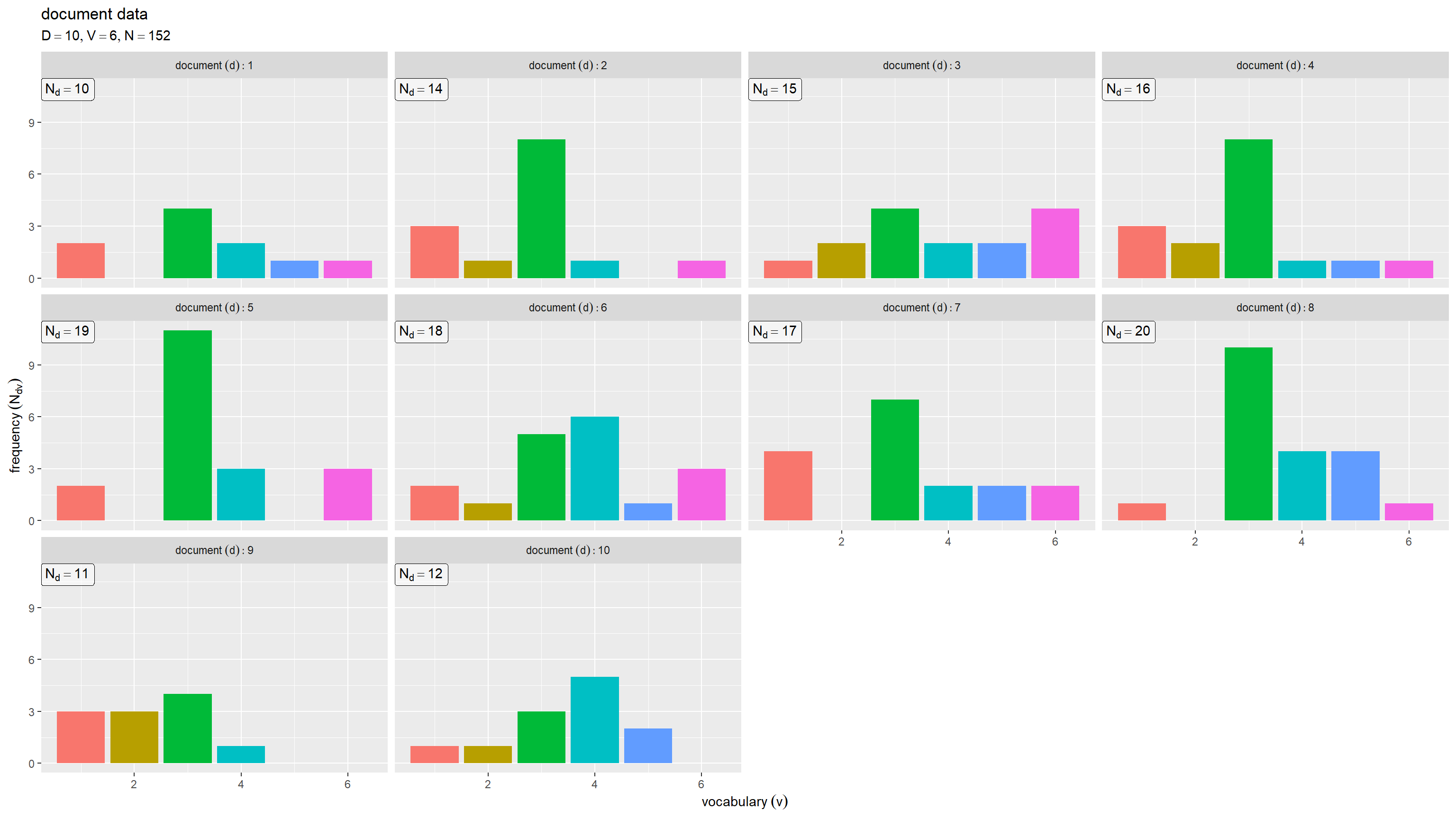
　横軸は語彙番号 $v$ 、縦軸は文書ごとの各語彙の出現回数 $N_{dv}$ を表すグラフを文書ごとに縦横に並べる。

　全文書での語彙頻度をグラフで確認する。

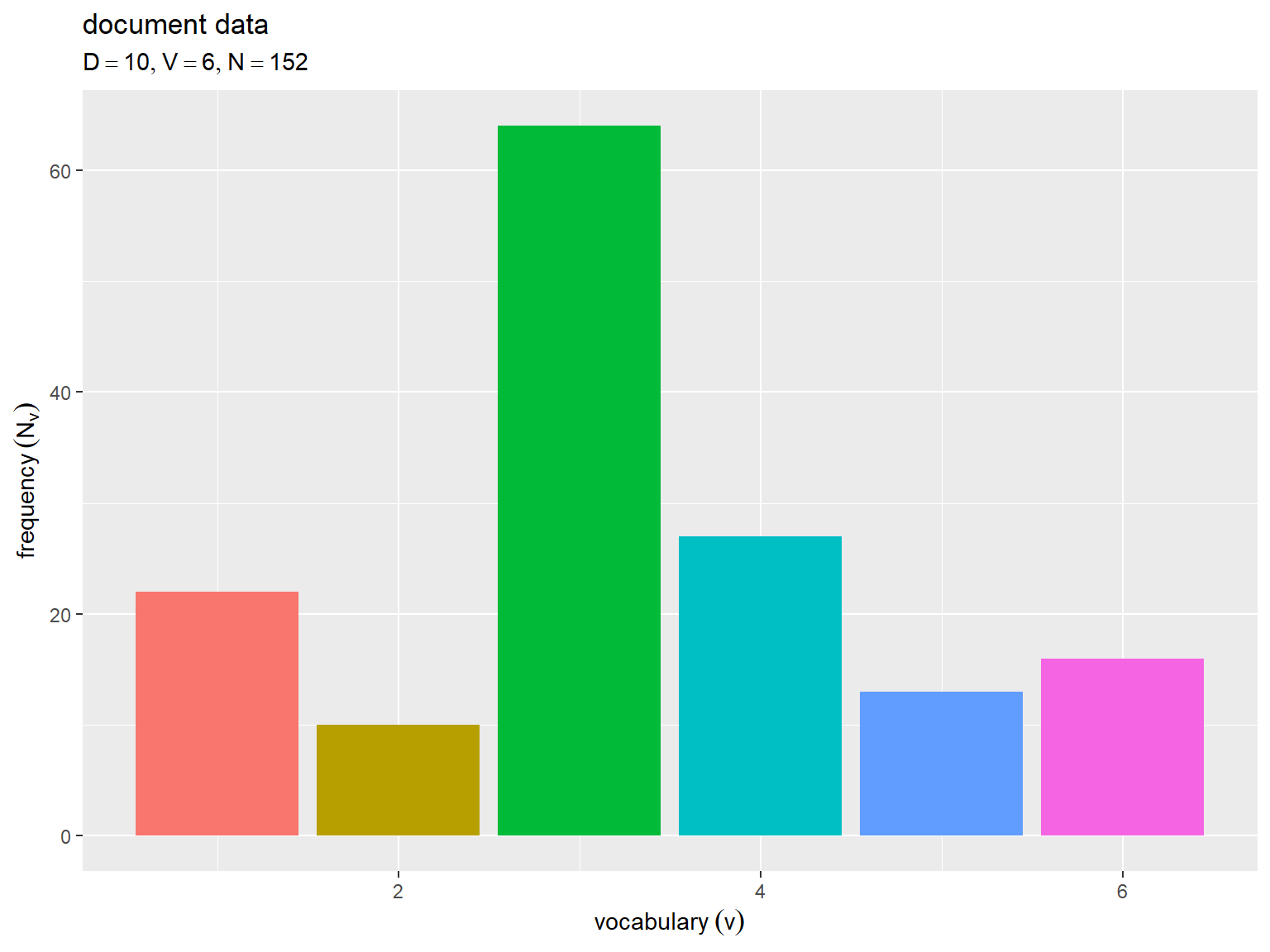
　横軸は語彙番号 $v$ 、縦軸は全文書での各語彙の出現回数 $N_v$ を表す。

　真の単語分布をグラフで確認する。

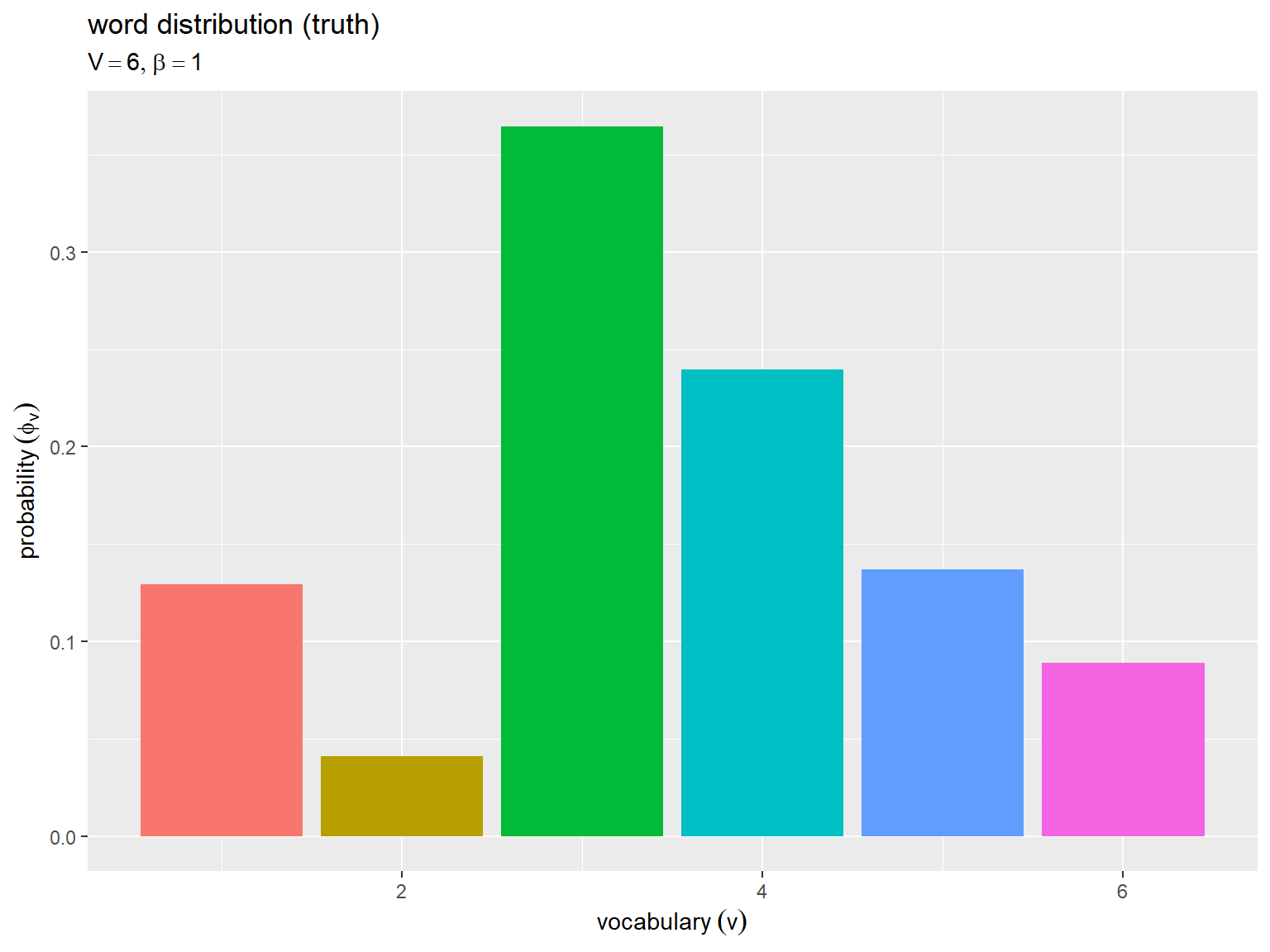
　横軸は語彙番号 $v$ 、縦軸は各語彙の出現(生成)確率 $\phi_v^{\mathrm{truth}}$ を表す。

　文書集合 $\mathbf{W}$ から得られる語彙頻度データ $(N_{11}, \cdots, N_{DV})$ のみを用いてパラメータ類を推定する。

パラメータの推定

　次は、不動点反復法を用いた経験ベイズ推定によりハイパーパラメータを推定する。

　文書集合に関する値を設定する。

# 文書数を取得
D <- nrow(N_dv)

# 語彙数を取得
V <- ncol(N_dv)

# 全文書の単語数を取得
N <- sum(N_dv)

# 各文書の単語数を取得
N_d <- rowSums(N_dv)

# 各語彙の出現回数を取得
N_v <- colSums(N_dv)
D; V; N; N_d; N_v

[1] 10
[1] 6
[1] 152
[1] 10 14 15 16 19 18 17 20 11 12
[1] 22 10 64 27 13 16

　観測データ N_dv から文書数 $D$ 、語彙数 $V$ 、単語数 $N = \sum_{d=1}^D \sum_{v=1}^V N_{dv}$ 、各文書の単語数 $(N_1, \cdots, N_D)$ 、 $N_d = \sum_{v=1}^V N_{dv}$ 、各語彙の単語数 $(N_1, \cdots, N_V)$ 、 $N_v = \sum_{d=1}^D N_{dv}$ を取得する。

　ハイパーパラメータの初期値と事前確率のパラメータを設定する。

# 単語分布のハイパーパラメータを指定
beta <- 10

# 単語分布のハイパーパラメータの事前分布のパラメータを指定
c <- 2
d <- 2

　単語分布の事前分布(ディリクレ分布)のパラメータの初期値 $\beta^{(0)} \gt 0$ 、ハイパーパラメータ $\beta$ の事前分布(ガンマ分布)のパラメータ $c \gt 0, d \gt 0$ を指定する。

　試行回数または閾値を指定して、不動点反復法によりハイパーパラメータを繰り返し更新する。

# 最大試行回数・閾値を指定
max_iter  <- 100
threshold <- 0.00001

# 初期値を記録
trace_beta_i    <- rep(NA, times = max_iter+1)
trace_beta_i[1] <- beta

# 不動点反復法によるMAP推定
for(i in 1:max_iter) {
  
  # 更新前の値を保存
  old_beta <- beta
  
  # ハイパーパラメータを更新
  tmp_denom <- sum(digamma(N_v + beta) - digamma(beta))
  tmp_numer <- V * (digamma(N + V*beta) - digamma(V*beta))
  beta      <- (c-1 + beta * tmp_denom) / (d + tmp_numer)
  
  # 更新値を記録
  trace_beta_i[i+1] <- beta
  
  # 途中経過を表示
  print(paste0("iteration: ", i, ", beta: ", round(beta, digits = 5)))
  
  # 収束すると終了
  if(abs(old_beta - beta) < threshold) {
    
    # 試行回数を記録
    max_iter <- i
    trace_beta_i <- trace_beta_i[1:(max_iter+1)]
    
    break
  }
}

[1] "iteration: 1, beta: 7.55197"
[1] "iteration: 2, beta: 5.92904"
[1] "iteration: 3, beta: 4.8027"
[1] "iteration: 4, beta: 3.99365"
[1] "iteration: 5, beta: 3.39668"
(省略)
[1] "iteration: 60, beta: 1.2005"
[1] "iteration: 61, beta: 1.20048"
[1] "iteration: 62, beta: 1.20047"
[1] "iteration: 63, beta: 1.20046"
[1] "iteration: 64, beta: 1.20045"

　ハイパーパラメータ $\beta$ の初期値を $\beta^{(0)}$ 、 $i$ 回目の更新値を $\beta^{(i)}$ として、次の式で値を更新する。

$\displaystyle \beta^{(i)} = \frac{ c - 1 + \beta^{(i-1)} \left( \sum_{v=1}^V \Psi \Bigl( N_v + \beta^{(i-1)} \Bigr) - V \Psi \Bigl( \beta^{(i-1)} \Bigr) \right) }{ d + V \Psi \Bigl( N + V \beta^{(i-1)} \Bigr) - V \Psi \Bigl( V \beta^{(i-1)} \Bigr) }$

　更新幅(更新前後の差の絶対値)が閾値 threshold 未満になると収束とみなしてループを終了する。収束しない場合は指定した回数 max_iter までループ処理する。

推定結果の可視化

　続いて、推定したパラメータや分布のグラフを作成する。
　アニメーションなどの作図コードは「map_estimation_hyparam.R」を参照のこと。

パラメータの図

　単語分布のハイパーパラメータの推移の描画用のデータフレームを作成する。

# 更新値を格納
trace_beta_df <- tibble::tibble(
  iter  = 0:max_iter, 
  value = trace_beta_i
)
trace_beta_df

# A tibble: 65 × 2
    iter value
   <int> <dbl>
 1     0 10   
 2     1  7.55
 3     2  5.93
 4     3  4.80
 5     4  3.99
 6     5  3.40
 7     6  2.95
 8     7  2.60
 9     8  2.33
10     9  2.12
# ℹ 55 more rows

　試行番号 $i$ とハイパーパラメータの更新値 $\beta^{(i)}$ を格納する。

　単語分布のハイパーパラメータの推移のグラフを作成する。

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "beta^{(0)} == ", trace_beta_i[1], ", ", 
  "beta^{(", max_iter, ")} == ", round(beta, digits = 3), ", ", 
  "c == ", c, ", ", 
  "d == ", d, 
  ")"
)

# 単語分布のハイパーパラメータの推移を作図
ggplot() + 
  geom_line(data = trace_beta_df, 
            mapping = aes(x = iter, y = value), 
            color = "navyblue") + # 更新値
  labs(title = "hyperparameter of word distribution (maximum a posteriori estimation)", 
       subtitle = parse(text =param_label), 
       y = expression(value~(beta^{(i)})), 
       x = expression(iteration~(i)))

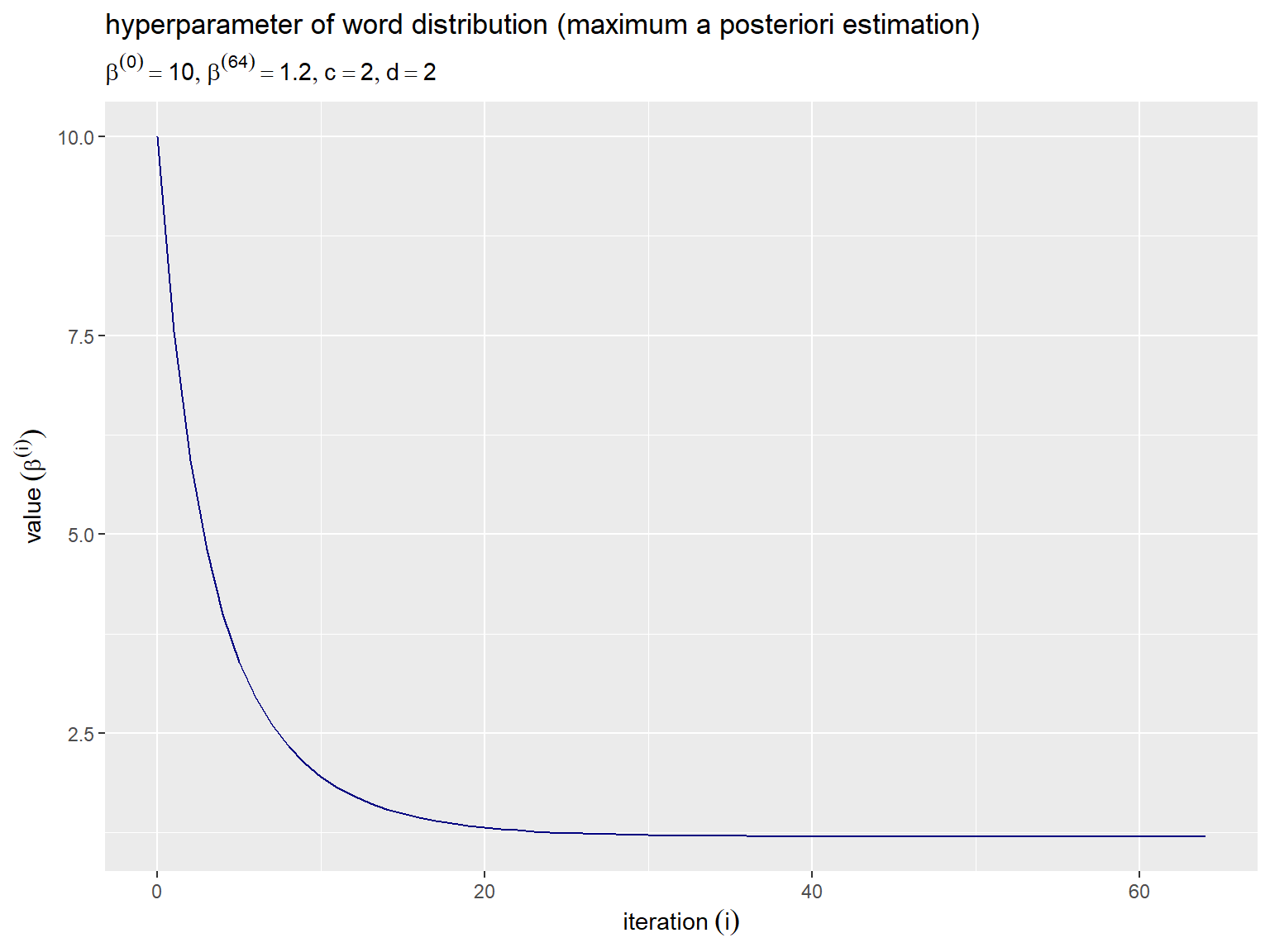
　横軸は試行回数 $i$ 、縦軸は $i$ 回目の更新値 $\beta^{(i)}$ を表す。

分布の図

　推定したハイパーパラメータを用いてパラメータを計算する。

# 単語分布のパラメータを計算
phi_v <- (N_v + beta-1) / (N + V * (beta-1))
phi_v

[1] 0.1449090 0.0665814 0.4190556 0.1775455 0.0861633 0.1057452

　パラメータのMAP推定値 $\boldsymbol{\phi}^{\mathrm{MAP}}$ は、収束した値 $\beta^{(i)}$ をハイパーパラメータのMAP推定値 $\beta^{\mathrm{MAP}}$ として、次の式で計算できる。

$\displaystyle \phi_v^{\mathrm{MAP}} = \frac{ N_v + \beta^{\mathrm{MAP}} - 1 }{ N + V (\beta^{\mathrm{MAP}} - 1) }$

　MAP推定によるパラメータ推定については「パラメータ推定」を参照のこと。

　単語分布のグラフを作成する。

# 真の単語分布を格納
true_phi_df <- tibble::tibble(
  v    = 1:V, 
  prob = true_phi_v
)

# 推定した単語分布を格納
phi_df <- tibble::tibble(
  v    = 1:V, 
  prob = phi_v
)

# ハイパーパラメータによる基準値を格納
beta_df <- tibble::tibble(
  v    = 1:V, 
  base = (beta-1) / (N + V * (beta-1))
)

# ラベル用の文字列を作成
param_label <- paste0(
  "list(", 
  "beta^{(", max_iter, ")} == ", round(beta, digits = 3), ", ", 
  "c == ", c, ", ", 
  "d == ", d, ", ", 
  "N == ", N, 
  ")"
)

# 凡例用の設定を格納
linetype_lt <- list(
  fill      = c("gray", NA, NA), 
  color     = c(NA, "red", "navyblue"), 
  linewidth = 0.5, 
  pattern   = c("none", "none", "crosshatch")
)

# 単語分布を作図
ggplot() + 
  geom_bar(data = phi_df, 
           mapping = aes(x = v, y = prob, fill = factor(v), linetype = "estimated"), 
           stat = "identity", show.legend = FALSE) + # 推定した分布
  ggpattern::geom_bar_pattern(
    data = beta_df, 
    mapping = aes(x = v, y = base, linetype = "hyparam"), stat = "identity", 
    fill = NA, color = "navyblue", pattern_fill = "navyblue", pattern_color = NA, 
    pattern = "crosshatch", pattern_density  = 0.05, pattern_spacing  = 0.08
  ) + # ハイパラによる基準値
  geom_bar(data = true_phi_df, 
           mapping = aes(x = v, y = prob, linetype = "true"), 
           stat = "identity", show.legend = FALSE, 
           fill = NA, color = "red", linewidth = 1) + # 真の分布
  scale_linetype_manual(breaks = c("estimated", "true", "hyparam"), 
                        values = c("solid", "dashed", "dotted"), 
                        labels = c("estimated", "true", "hyperparameter"), 
                        name = "distribution") + # 凡例の表示用
  guides(fill = "none", 
         linetype = guide_legend(override.aes = linetype_lt)) + # 凡例の体裁
  labs(title = "word distribution (maximum a posteriori estimation)", 
       subtitle = parse(text = param_label), 
       x = expression(vocabulary ~ (v)), 
       y = expression(probability ~ (phi[v])))

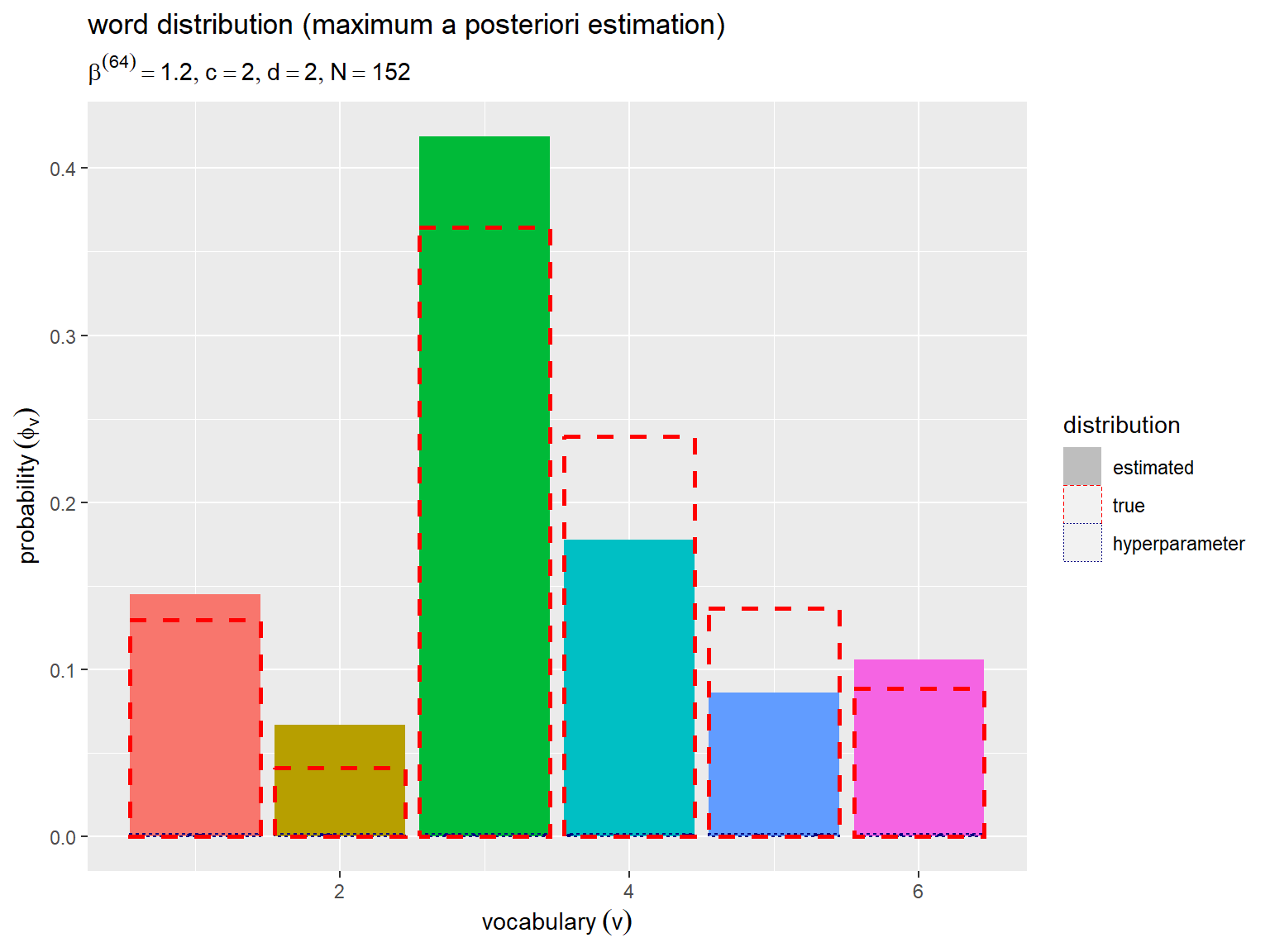
　横軸は語彙番号 $v$ 、縦軸は各語彙の出現確率 $\phi_v$ を表す。
　真の分布を赤色の破線、推定した分布を塗りつぶしで示す。また、ハイパーパラメータによる全ての語彙への一定の影響範囲を紺色の点線で示す。語彙ごとの値は出現回数 $N_v$ の影響を受けるのが $\phi_v$ 計算式から分かる。

　単語分布の推移をアニメーションで確認する。

　 $\beta$ が大きい(小さい)ほど全体への影響が強く(弱く)なるのを確認できる。ハイパーパラメータの値を調整して、真の分布の形状に近付いている。

　KL情報量の推移をグラフで確認する。

# KL情報量の推移を作図
ggplot() + 
  geom_line(data = anim_label_df, 
            mapping = aes(x = iter, y = KL)) + # KL情報量
  labs(title = "KL divergence (maximum a posteriori estimation)", 
       x = expression(iteration ~ (i)), 
       y = expression(value ~ (KL(list(phi^{truth}, phi^{MAP})))))

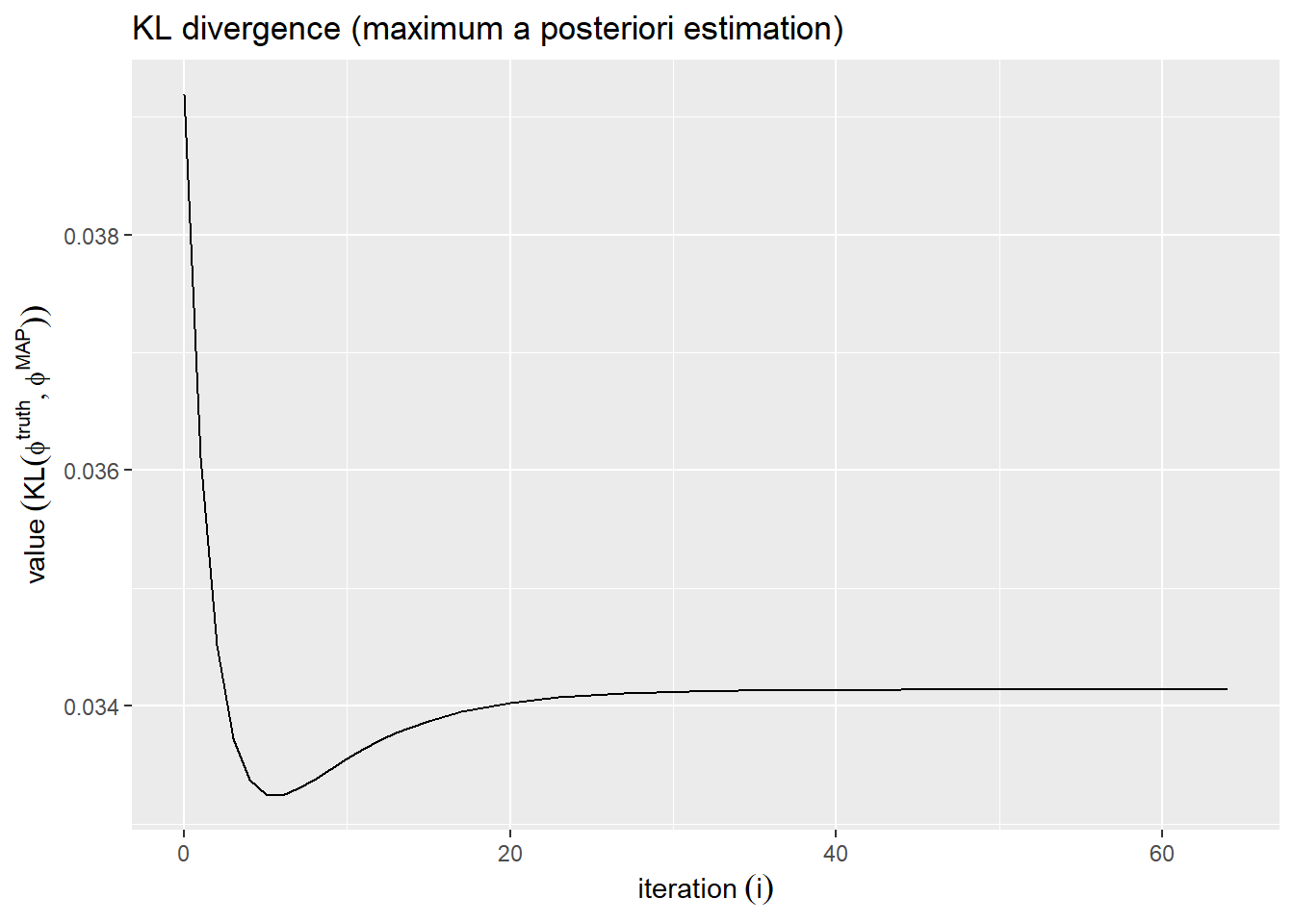
　横軸は試行回数 $i$ 、縦軸は真のパラメータ $\boldsymbol{\phi}^{\mathrm{truth}}$ と $i$ 回目の更新値 $\beta^{(i)}$ を用いて求めたMAP推定値 $\boldsymbol{\phi}^{\mathrm{MAP}}$ のKL情報量を表す。

推定への影響の可視化

　最後は、推定結果へのハイパーパラメータなどの影響をグラフで確認する。

パラメータの影響

　ハイパーパラメータの初期値やハイパーパラメータの事前分布のパラメータの影響をグラフで確認する。

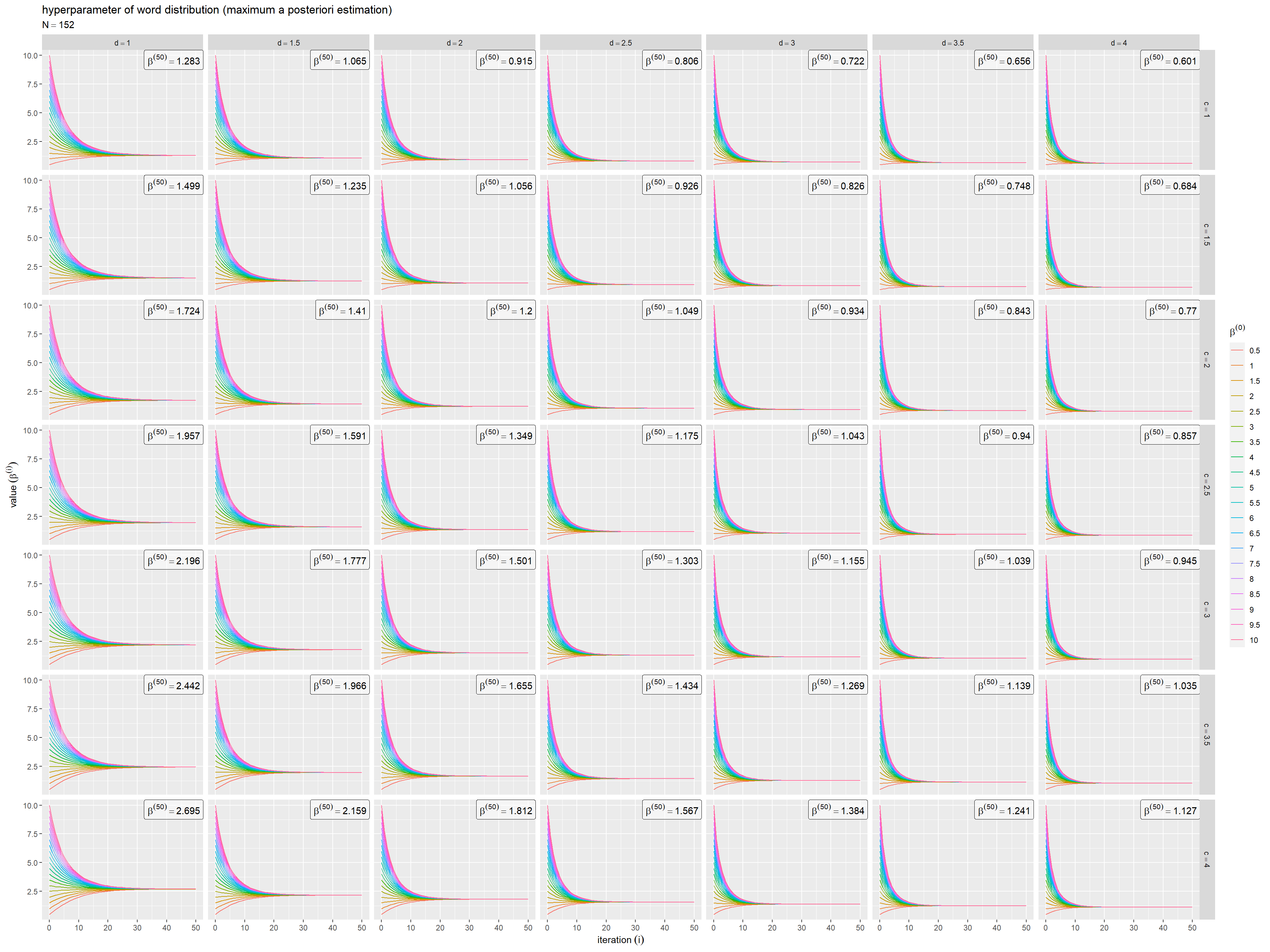
　横軸は試行回数 $i$ 、縦軸は $i$ 回目の更新値 $\beta^{(i)}$ を表す。ハイパーパラメータの初期値 $\beta^{(0)}$ の影響を同じグラフ内に曲線を並べて比較する。 $\beta$ の事前分布(ガンマ分布)の形状パラメータ $c$ の影響を縦方向、逆尺度パラメータ $d$ の影響を横方向にグラフを並べて比較する。

　初期値や事前分布のパラメータに関わらず収束している。各グラフの右上の収束値のラベルは、参考として1例を表示している。
　 $\beta$ の更新式からも分かる通り、 $c$ が大きいほど $\beta$ も大きく、 $c$ が大きいほど $\beta$ 小さくなるように影響する。

　この記事では、ユニグラムモデルにおける不動点反復法によるハイパーパラメータのMAP推定をプログラムで確認した。
　またこの章では、ユニグラムモデルを扱った。次章では、混合ユニグラムモデルを扱う。

参考書籍

岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社

おわりに

　疑似コードがないので悩んだのですが組んでみました。

　2024年5月7日は、モーニング娘。の元メンバーの佐藤優樹さんの25歳のお誕生日です！

　まーちゃんがもう25歳！おめでとうございます。
　佐藤優樹さんがいなければ私がハロプロにハマることもなくこのブログもなかったです。ぜひ聴いてください。

【次節の内容】

つづく

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【R】2.7：ユニグラムモデルのMAP推定の実装：ハイパーパラメータ推定【青トピックモデルのノート】