はじめに

　『トピックモデル』(MLPシリーズ)の勉強会資料のまとめです。各種モデルやアルゴリズムを「数式」と「プログラム」を用いて解説します。
　本の補助として読んでください。

　この記事では、トピックモデルにおいて周辺尤度を最大化するために不動点反復法を行う際に利用する対数ガンマ関数とディガンマ関数の不等式の行間を埋めます。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

はじめに
対数ガンマ関数とディガンマ関数の不等式の導出
参考書籍
おわりに

対数ガンマ関数とディガンマ関数の不等式の導出

　ガンマ関数(gamma function)とディガンマ関数(digamma funciton・プサイ関数・psi function)の関係から、トピックモデル(topic models)における周辺尤度関数(marginal likelihood function)の下限を求めるための不等式を導出する。周辺尤度に対して不動点反復法(固定点反復法・fixed-point iteration)を行うための式変形に利用する。
　ガンマ関数については「【R】ガンマ関数の作図 - からっぽのしょこ」、ディガンマ関数については「【R】ディガンマ関数の作図 - からっぽのしょこ」を参照のこと。

作図コード(クリックで展開)

　利用するパッケージを読み込む。

# 利用パッケージ
library(tidyverse)

　この記事では、基本的に パッケージ名::関数名() の記法を使うので、パッケージの読み込みは不要である。ただし、作図コードについてはパッケージ名を省略するので、ggplot2 を読み込む必要がある。
　また、ネイティブパイプ演算子 |> を使う。magrittrパッケージのパイプ演算子 %>% に置き換えられるが、その場合は magrittr を読み込む必要がある。

ガンマ関数とディガンマ関数の関係

　まずは、対数をとったガンマ関数とディガンマ関数の関係をグラフと数式で確認する。

　ディガンマ関数 $\Psi(x)$ は、ガンマ関数 $\Gamma(x)$ の対数微分で定義される。

$\displaystyle \Psi(x) = \frac{ \mathrm{d} \log \Gamma(x) }{ \mathrm{d} x } \tag{1}$

　ガンマ関数と対数ガンマ関数、ディガンマ関数をグラフで確認する。

作図コード(クリックで展開)

# x軸の範囲を指定
x_vec <- seq(from = 0, to = 10, length.out = 5001)
x_vec[x_vec == 0] <- 1e-10 # (x = 0のときInfになり意図しない作図処理になるのを回避)

# 関数の曲線の座標を作成
fnc_curve_df <- tibble::tibble(
  x           = x_vec, 
  digamma_x   = digamma(x), 
  log_gamma_x = lgamma(x), 
  gamma_x     = gamma(x)
) |> 
  tidyr::pivot_longer(
    cols      = !x, 
    names_to  = "fnc", 
    values_to = "f_x"
  ) # 関数の値を1列にまとめる

# 軸サイズを指定
axis_y_size <- 10

# 配色の共通化用のカラーコードを作成
color_vec <- scales::hue_pal()(n = 4)

# ディガンマ関数を作図
graph <- ggplot() + 
  geom_segment(mapping = aes(x = c(-Inf, 0), y = c(0, -Inf), 
                             xend = c(Inf, 0), yend = c(0, Inf)), 
               arrow = arrow(length = unit(10, units = "pt"), ends = "last")) + # x・y軸線
  geom_line(data = fnc_curve_df, 
            mapping = aes(x = x, y = f_x, color = fnc)) + # 関数曲線
  scale_color_manual(breaks = c("digamma_x", "log_gamma_x", "gamma_x"), 
                     values = color_vec[1:3], 
                     labels = c(expression(Psi(x)), expression(log~Gamma(x)), expression(Gamma(x))), 
                     name = "function") + # 凡例の表示用
  coord_cartesian(xlim = c(0, max(x_vec)), 
                  ylim = c(-axis_y_size, axis_y_size)) + # 描画領域の設定
  labs(title = "gamma function and digamma function", 
       subtitle = expression(Psi(x) == frac(d ~ log~Gamma(x), d ~ x)), 
       x = expression(x), 
       y = expression(f(x)))

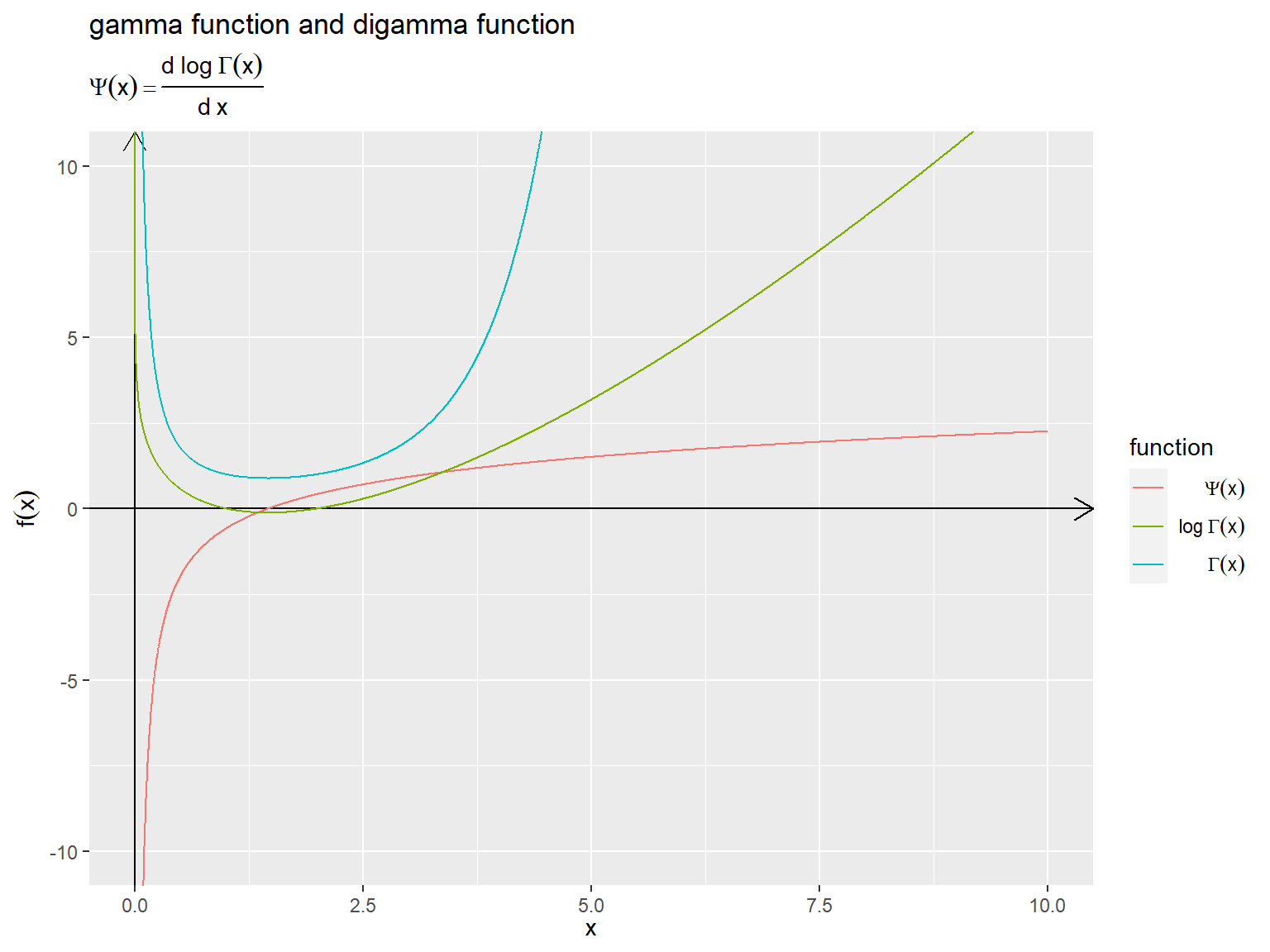
　ディガンマ関数の単調増加性を確認できる。

　対数ガンマ関数とディガンマ関数の関係をアニメーションで確認する。

　対数ガンマ関数の曲線に対する接線の傾きとディガンマ関数が一致するのを確認できる。

　対数ガンマ関数の曲線上の2点とディガンマ関数の関係をアニメーションで確認する。

　曲線上の2点を通る直線の傾きと接線の傾きの大小関係を確認できる。

　曲線上の2点 $(x, y) = (x_i, \log \Gamma(x_i))$ を通る直線 $y = \alpha x + \beta$ の傾き $\alpha$ と切片 $\beta$ は、次の式である。

$\displaystyle \begin{aligned} \alpha &= \frac{ \log \Gamma(x_2) - \log \Gamma(x_1) }{ x_2 - x_1 } \\ \beta &= y_i - \alpha x_i \end{aligned}$

　傾きの計算式に関して、 $h = x_2 - x_1$ とおき $h$ を限りなく $0$ ( $x_2$ を $x_1$ )に近付けると、微分の定義なので、ディガンマ関数になる。

$\displaystyle \Psi(x_1) = \lim_{h \rightarrow 0} \frac{ \log \Gamma(x_1 + h) - \log \Gamma(x_1) }{ h }$

　ディガンマ関数の単調増加性から、対数ガンマ関数曲線上の2点を通る直線の傾き $\frac{\log \Gamma(x_2) - \log \Gamma(x_1)}{x_2 - x_1}$ と変数(x軸)が小さい方の点に対する接線の傾き $\Psi(x_1)$ は、次の関係である。

$\displaystyle \frac{\log \Gamma(x_2) - \log \Gamma(x_1)}{x_2 - x_1} \gt \Psi(x_1) \qquad (0 \lt x_1 \lt x_2) \tag{2}$

　(対数)ガンマ関数とディガンマ関数の関係を示す不等式が得られた。
　 $x_1 = x_2$ のとき0除算になるため定義できない。 $x_1 \gt x_2$ のとき大小関係が反転する。

$\displaystyle \frac{\log \Gamma(x_2) - \log \Gamma(x_1)}{x_2 - x_1} \lt \Psi(x_1) \qquad (x_1 \gt x_2 \gt 0)$

　変数(x軸)が大きい方の点に対する接線の傾きとの比較と言える。

　式(2)を $\log \Gamma(x_2)$ について整理して、両辺で指数をとる。

$\displaystyle \begin{align} && \log \Gamma(x_2) &\geq \log \Gamma(x_1) + (x_2 - x_1) \Psi(x_1) \qquad (0 \lt x_1 \leq x_2) \tag{3}\\ \Rightarrow && \Gamma(x_2) &\geq \Gamma(x_1) \exp \Bigl( (x_2 - x_1) \Psi(x_1) \Bigr) \end{align}$

　ガンマ関数についての式が得られた。
　 $x_1 = x_2$ のとき等式が成り立つ。

対数ガンマ関数のテイラー展開

　続いて、対数ガンマ関数のテイラー展開(Taylor expansion・テイラー級数・Taylor series)を導出する。

　テイラー展開により対数ガンマ関数を近似する。

$\displaystyle \begin{align} \log \Gamma(x) &\approx \sum_{i=0}^{\infty} \frac{\{\log \Gamma(a)\}^{(i)}}{i!} (x - a)^i \tag{4}\\ &= \frac{\log \Gamma(a)}{0!} (x - a)^0 + \frac{\{\log \Gamma(a)\}'}{1!} (x - a)^1 \\ &\qquad + \frac{\{\log \Gamma(a)\}''}{2!} (x - a)^2 + \frac{\{\log \Gamma(a)\}'''}{3!} (x - a)^3 + \cdots \\ &= \log \Gamma(a) + \Psi(a) (x - a) \\ &\qquad + \frac{\{\Psi(a)\}'}{2} (x - a)^2 + \frac{\{\Psi(a)\}''}{6} (x - a)^3 + \cdots \end{align}$

途中式の途中式(クリックで展開)

1: 対数ガンマ関数 $\log \Gamma(x)$ に対して $a$ の周りでテイラー展開 $f(x) \approx \sum_{i=0}^{\infty} \frac{f^{(i)}(a)}{i!} (x - a)^i$ $f^{(i)}(x)$ を行う。 $f^{(i)}(x), {f(x)}^{(i)}$ は関数 $f(x)$ の $i$ 階微分を表す。
2: 例として、3次の項まで書き出す。
3: ディガンマ関数の定義(1)より、2番目の項を置き換える。また定義より、 $0! = 1$ 、 $x^0 = 1$ である。

　ディガンマ関数も含めて、対数ガンマ関数のn回微分をポリガンマ関数と呼ぶ。

　対数ガンマ関数のテイラー展開をアニメーションで確認する。

・100次まで

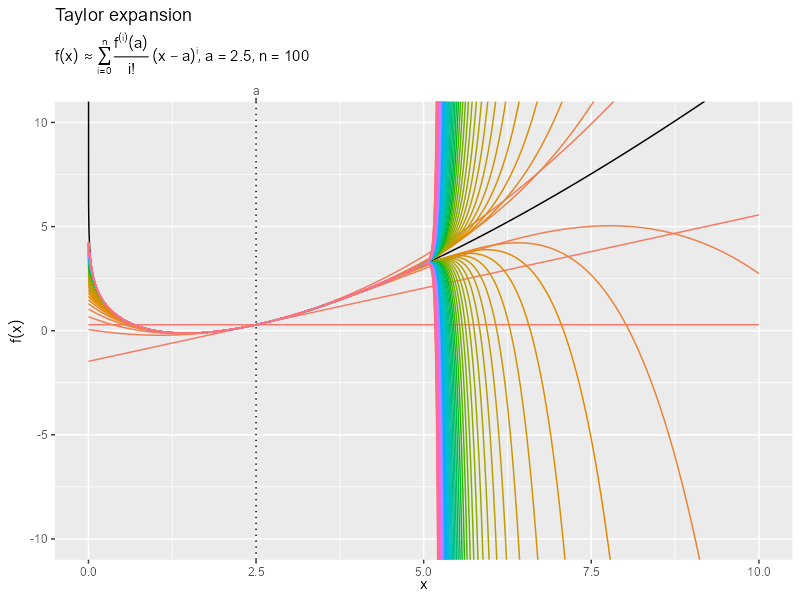
・10次まで

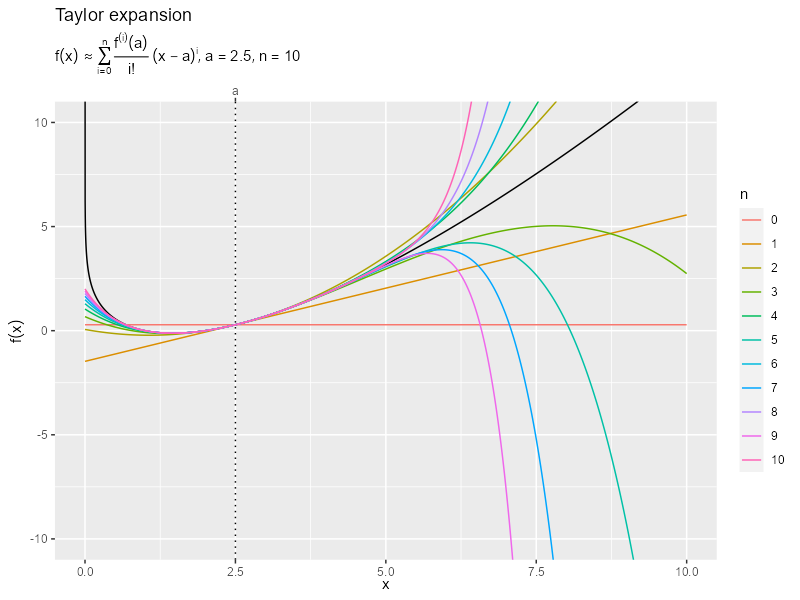
　0次の項 $\log \Gamma(a)$ は、点 $(a, f(x))$ を通る水平線を表す。1次までの項の和 $\log \Gamma(a) + (x - a) \Psi(a)$ は、点 $(a, f(x))$ に対する接線を表す。
　次数の数 $n$ を大きくする(項の数を増やす)ほど $a$ 付近の近似が良くなるのを確認できる。

　 $x \lt a$ のとき「対数ガンマ関数とディガンマ関数の関係」より、式(3)の関係が得られる。

$\displaystyle \begin{align} \log \Gamma(x) \geq \log \Gamma(a) + (x - a) \Psi(a) \qquad (0 \lt a \lt x) \end{align}$

トピックモデルにおける不等式の導出

　次は、トピックモデル全般のモデル(カテゴリ分布とディリクレ分布によるモデル)で登場する周辺尤度関数の下限として用いる式を導出する。

　トピックモデルでは、カテゴリ分布(尤度)とディリクレ分布(事前分布)の同時分布(結合分布)に関して、カテゴリ分布のパラメータを周辺化したポリヤ分布(周辺尤度)が登場する。

$\displaystyle p(\mathbf{W} | \mathbf{z}, \beta) = \prod_{k=1}^K \left\{ \frac{\Gamma(V \beta)}{\Gamma(N_k + V \beta)} \prod_{v=1}^V \frac{\Gamma(N_{kv} + \beta)}{\Gamma(\beta)} \right\} \tag{5}$

　 $K$ をカテゴリ数、 $V$ を観測データの種類数として、 $N_k, N_{kv}$ は観測データ(文書データ)に割り当てられたカテゴリ(トピック)ごとのカウント(単語数)を表す。 $\beta$ はハイパーパラメータであり尤度関数の変数として扱う。
　詳しくは「2.2：ユニグラムモデルの生成モデルの導出【青トピックモデルのノート】 - からっぽのしょこ」を参照のこと。

　記号の設定はモデルによって異なるので、カウントを $n$ 、ハイパーパラメータ(変数)を $x$ として考える。

　式(5)の前の項に関して、対数をとって $\hat{x}$ の周りで1次までテイラー展開する。

$\displaystyle \begin{align} \log \left( \frac{\Gamma(x)}{\Gamma(n + x)} \right) &= \log \Gamma(x) - \log \Gamma(n + x) \\ &\approx \Bigl( \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) \Bigr) \\ &\qquad + (x - \hat{x}) \frac{\mathrm{d}}{\mathrm{d} x} \Bigl\{ \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) \Bigr\} \\ &= \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) \\ &\qquad + (x - \hat{x}) \left( \frac{\mathrm{d} \log \Gamma(\hat{x})}{\mathrm{d} x} - \frac{\mathrm{d} \log \Gamma(n + \hat{x})}{\mathrm{d} x} \right) \\ &= \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) + (x - \hat{x}) \Bigl( \Psi(\hat{x}) - \Psi(n + \hat{x}) \Bigr) \\ &= \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) + (\hat{x} - x) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \end{align}$

途中式の途中式(クリックで展開)

1: 対数の性質 $\log \frac{x}{y} = \log x - \log y$ より、分数を分割する。
2: $f(x) = \log \Gamma(x) - \log \Gamma(x + x)$ として、2次までテイラー展開(4)する。
3: 和の微分 $(f(x) + g(x))' = f'(x) + g'(x)$ より、項ごとの微分の和に分割する。
4: ディガンマ関数の定義(1)より、対数ガンマ関数の微分をディガンマ関数に置き替える。
5: 式(5)の後の項に関する式(9)に対応させるため、最後の項に $(-1) (-1) = 1$ を掛けて(それぞれの括弧から $-1$ を括り出して)、括弧内の差を入れ替える。

　近似式を不等式に置き換えて、両辺で指数をとる。

$\displaystyle \begin{aligned} && \log \left( \frac{\Gamma(x)}{\Gamma(n + x)} \right) &\geq \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) + (\hat{x} - x) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \\ \Rightarrow && \exp \left( \log \left( \frac{\Gamma(x)}{\Gamma(n + x)} \right) \right) &\geq \exp \Biggl( \log \Gamma(\hat{x}) - \log \Gamma(n + \hat{x}) + (\hat{x} - x) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \Biggr) \\ && &= \exp \left( \log \left( \frac{\Gamma(\hat{x})}{\log \Gamma(n + \hat{x})} \right) \right) \exp \Biggl( (\hat{x} - x) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \Biggr) \\ \Rightarrow && \frac{\Gamma(x)}{\Gamma(n + x)} &\geq \frac{\Gamma(\hat{x})}{\Gamma(n + \hat{x})} \exp \Biggl( (\hat{x} - x) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \Biggr) \end{aligned}$

途中式の途中式(クリックで展開)

1: (近似を下限に置き換えられる理由が分かりません。教えてください…)
2: 両辺それぞれで全体をネイピア数 $e$ の指数 $e^x = \exp(x)$ にする。
3: 指数の性質 $e^{n+m} = e^n e^m$ より、和が積になる。
3: 対数の性質 $\log \frac{x}{y} = \log x - \log y$ より、差が商になる。
4: 指数と対数の関係 $x = \exp(\log x)$ より、 $\log$ を外す。

　右辺について

$\displaystyle b = \Psi(n + \hat{x}) - \Psi(\hat{x}) \tag{6}$

とおく。

$\displaystyle \frac{\Gamma(x)}{\Gamma(n + x)} \geq \frac{ \Gamma(\hat{x}) \exp \Bigl( (\hat{x} - x) b \Bigr) }{ \Gamma(n + \hat{x}) } \tag{7}$

　周辺尤度(5)の前の項の下限が得られた。

　同様に、式(5)の後の項の対数に関して、 $\hat{x}$ の回りで1次までテイラー展開する。

$\displaystyle \begin{aligned} \log \left( \frac{\Gamma(n + x)}{\Gamma(x)} \right) &= \log \Gamma(n + x) - \log \Gamma(x) \\ &\approx \Bigl( \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) \Bigr) \\ &\qquad + (x - \hat{x}) \frac{\mathrm{d}}{\mathrm{d} x} \Bigl\{ \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) \Bigr\} \\ &= \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) \\ &\qquad + (x - \hat{x}) \left( \frac{\mathrm{d} \log \Gamma(n + \hat{x})}{\mathrm{d} x} - \frac{\mathrm{d} \log \Gamma(\hat{x})}{\mathrm{d} x} \right) \\ &= \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) + (x - \hat{x}) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \\ &= \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) + \frac{x - \hat{x}}{\hat{x}} \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \\ &\approx \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) + (\log x - \log \hat{x}) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \end{aligned}$

途中式の途中式(クリックで展開)

1-4: 式(5)の前の項のときと同様にして変形する。
5: 対数変化率の形にするために、最後の項に $\frac{\hat{x}}{\hat{x}} = 1$ を分割して掛ける。
6: 対数変化率の性質 $\log \frac{Y}{X} \approx \frac{Y - X}{X}$ より、分数の項を対数の差に置き換える(近似する)。(意図が分からない。微分した後に $x, \hat{x}$ を残すため？)

　近似式を不等式に置き換えて、両辺で指数をとる。

$\displaystyle \begin{aligned} && \log \left( \frac{\Gamma(n + x)}{\Gamma(x)} \right) &\geq \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) + (\log x - \log \hat{x}) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \\ \Rightarrow && \exp \Bigl( \log \left( \frac{\Gamma(n + x)}{\Gamma(x)} \right) \Bigr) &\geq \exp \Biggl( \log \Gamma(n + \hat{x}) - \log \Gamma(\hat{x}) + (\log x - \log \hat{x}) \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \Biggr) \\ && &= \exp \left( \log \left( \frac{\Gamma(n + \hat{x})}{\Gamma(\hat{x})} \right) \right) \exp \left( \log \left( \frac{x}{\hat{x}} \right) \right)^{ (\Psi(n + \hat{x}) - \Psi(\hat{x})) \hat{x} } \\ \Rightarrow && \frac{\Gamma(n + x)}{\Gamma(x)} &\geq \frac{\Gamma(n + \hat{x})}{\Gamma(\hat{x})} \left( \frac{x}{\hat{x}} \right)^{ (\Psi(n + \hat{x}) - \Psi(\hat{x})) \hat{x} } \end{aligned}$

途中式の途中式(クリックで展開)

1: (近似を下限に置き換えられる理由が分かりません。教えてください…)
3-4: 式(5)の前の項のときと同様にして変形する。
3: 指数の性質 $e^{n m} = (e^n)^m$ より、積がべき乗になる。

　右辺について

$\displaystyle \begin{aligned} a &= \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \\ c &= \frac{\Gamma(n + \hat{x})}{\Gamma(\hat{x})} \hat{x}^{-a} \end{aligned} \tag{8}$

とおいて、式を整理する。

$\displaystyle \begin{align} \frac{\Gamma(n + x)}{\Gamma(x)} &\geq \frac{\Gamma(n + \hat{x})}{\Gamma(\hat{x})} \left(\frac{x}{\hat{x}} \right)^a \\ &= \frac{\Gamma(n + \hat{x})}{\Gamma(\hat{x})} {\hat{x}}^{-a} x^a \\ &= c x^a \tag{9} \end{align}$

途中式の途中式(クリックで展開)

2: $(\frac{x}{x})^a = \frac{x^a}{x^a}$ 、 $\frac{1}{x^a} = x^{-a}$ より、分数のべき乗の項を分割する。

　周辺尤度(5)の後の項の下限が得られた。

　カウント( $n$ に対応する変数)は0以上の値、ハイパーパラメータ(ディリクレ分布のパラメータで $x, \hat{x}$ に対応する変数)は非負の値なので、2つの不等式のそれぞれの辺は常に正の値である。
　よって、それぞれの辺の積から、次の関係が成り立つ。

$\displaystyle \begin{aligned} \frac{\Gamma(x)}{\Gamma(n + x)} \prod_{i} \frac{\Gamma(n_i +x)}{\Gamma(x)} &\geq \frac{ \Gamma(\hat{x}) \exp \Bigl( (\hat{x} - x) b \Bigr) }{ \Gamma(n + \hat{x}) } \prod_{i} \frac{\Gamma(n_i + \hat{x})}{\Gamma(\hat{x})} {\hat{x}}^{-a} x^a \\ a &= \Bigl( \Psi(n_i + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \\ b &= \Psi(n + \hat{x}) - \Psi(\hat{x}) \end{aligned}$

　周辺尤度に関する $\hat{x}$ における不等式(下限の計算式)が得られた。

不動点反復法のための不等式

　周辺尤度関数を最大化するハイパーパラメータを求めるための不動点反復法に用いる式をまとめる。

　ガンマ関数 $\Gamma(x)$ とディガンマ関数 $\Psi(x)$ を用いて、次の関係が成り立つ。

$\displaystyle \begin{align} \frac{\Gamma(x)}{\Gamma(n + x)} &\geq \frac{\Gamma(\hat{x})}{\Gamma(n + \hat{x})} \exp \Bigl( (\hat{x} - x) b \Bigr) &&\quad (\hat{x} \geq 0, x \gt 0, n \geq 0) \tag{7}\\ b &= \Psi(n + \hat{x}) - \Psi(\hat{x}) \tag{6} \end{align}$

　 $\hat{x} = x$ のときに、 $e^0 = 1$ なので、等号が成り立つ。

　また、次の関係も成り立つ。

$\displaystyle \begin{align} \frac{\Gamma(n + x)}{\Gamma(x)} &\geq \frac{\Gamma(n + \hat{x})}{\Gamma(\hat{x})} \hat{x}^{-a} x^a &&\quad (\hat{x} \geq 0, x \gt 0, n \geq 1) \tag{9}\\ a &= \Bigl( \Psi(n + \hat{x}) - \Psi(\hat{x}) \Bigr) \hat{x} \tag{8} \end{align}$

　 $\hat{x} = 0$ のときに、 $x^0 = 1, 0^0 = 1$ なので、等号が成り立つ。

　 $\hat{x}$ を現在値、 $x$ を更新値として、周辺尤度を式(6-9)の関係に対応させて変形する。変形した式を周辺尤度の下限として、不動点反復法によりハイパーパラメータを繰り返し更新する。
　つまり、周辺尤度を現在値 $\hat{x}$ の周りで(1次まで)テイラー展開して、近似した周辺尤度を最大化するようにパラメータを更新する。

　この記事では、トピックモデルにおいて不動点反復法を行いハイパーパラメータするための対数尤度の下限の式を求めた。各種推論アルゴリズムを導出する際に利用する。

参考書籍

佐藤一誠(2015)『トピックモデルによる統計的潜在意味解析』(自然言語処理シリーズ 8),奥村学監修,コロナ社

おわりに

2024.05.07：加筆修正の際に「一様なハイパーパラメータの場合の経験ベイズ推定の導出」から記事を分割しました。

　これまで怪しいことを書いていました。いや最終的な式は合ってるんだから一周回って正しいんだろうけど理由を説明できません。今回の(あくまで構成を整えることが主目的だった)加筆修正で間違いに気付きました。
　じゃあどうすりゃ正しいんだとアレコレ式変形しても分からず投げる寸前でしたが、ふと思いついたテイラー展開で一発でした。この記事の内容が冗長なのは、思い付くまでの試行錯誤で作った図を落とさず載せたからです。折角なので回り道的な内容の方を膨らませて別記事に格上げしたいですが、またいずれ。
　初見でとは言わないにしてももう少し早く式の形からテイラー展開気付けてもおかしくないんだろうけど、いやーこういうとき独学の辛さを感じます。でもアレコレ苦しんだ末にパッと閃く感覚を知ってしまったらもう止めらんねぇです。

　とまぁキレイに締めたいのですが、近似式から不等式にするところが分かりませんでした。分かる方がいらっしゃいましたら教えてください。他の記事もですが、私がまだ気付いていない間違いがありましてたらそれも教えていただけるととても嬉しいです。お手数ですがお願いします。

　あとどうでもいい話ですが、この記事は青トピシリーズとして書いたのですが、青本では丸々飛ばされていて白本に載ってる内容なんですよね。白本の修正作業に移れたら、この記事の所属を鞍替えするかもしれません。

【次節の内容】

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

対数ガンマ関数とディガンマ関数の不等式の導出【青トピックモデルのノート】

はじめに

対数ガンマ関数とディガンマ関数の不等式の導出

ガンマ関数とディガンマ関数の関係

対数ガンマ関数のテイラー展開

トピックモデルにおける不等式の導出

不動点反復法のための不等式

参考書籍

おわりに