はじめに

　黄金比の定義や性質、黄金比を利用した図形やアルゴリズムについて、数式やプログラム、図を用いて理解を目指すシリーズです。

　この記事では、三分探索について図を使って解説します。

【他の内容】

www.anarchive-beta.com

【今回の内容】

はじめに
三分探索の可視化
参考文献
おわりに

三分探索の可視化

　三分割探索(ternary search)のアルゴリズムを図で確認します。
　効率的な三分探索である黄金分割探索については「【Python】黄金分割探索の可視化 - からっぽのしょこ」を参照してください。

　利用するライブラリを読み込みます。

# ライブラリを読込
import numpy as np
import matplotlib.pyplot as plt

関数の設定

　まずは、最小値(または最大値)の探索対象とする関数を設定します。この記事では、最小値の探索のみを扱います。

　自作関数を作成します。

# 関数を作成
def eval_fnc(x):

    # 計算式を指定
    y = 0.5 * x**2 - 4.0 * x + 12
    return y

　下に凸の関数(計算式)を指定します。上に凸の関数の場合は、-y を出力すると(簡易的に)扱えます。
　この例では、 $f(x) = \frac{1}{2} x^2 - 4 x + 12$ とします。

　変数の範囲を指定して、曲線の座標を作成します。

# 変数の範囲を指定
x_min = -5.0
x_max = 15.0

# 曲線用の変数を作成
x_vec = np.linspace(start=x_min, stop=x_max, num=1001)

# 関数曲線を計算
f_x_vec = eval_fnc(x_vec)

　変数 $x$ の範囲を指定して、関数 $f(x)$ を計算します。

　関数のグラフを作成します。

# ラベル用の文字列を作成
fnc_label = '$f(x) = 0.5 x^2 - 4 x + 12$'

# 関数曲線を作図
fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white', 
                       constrained_layout=True)
ax.plot(x_vec, f_x_vec, color='black', label=fnc_label) # 関数
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x)$')
fig.suptitle('convex function', fontsize=20)
ax.grid()
ax.legend()
plt.show()

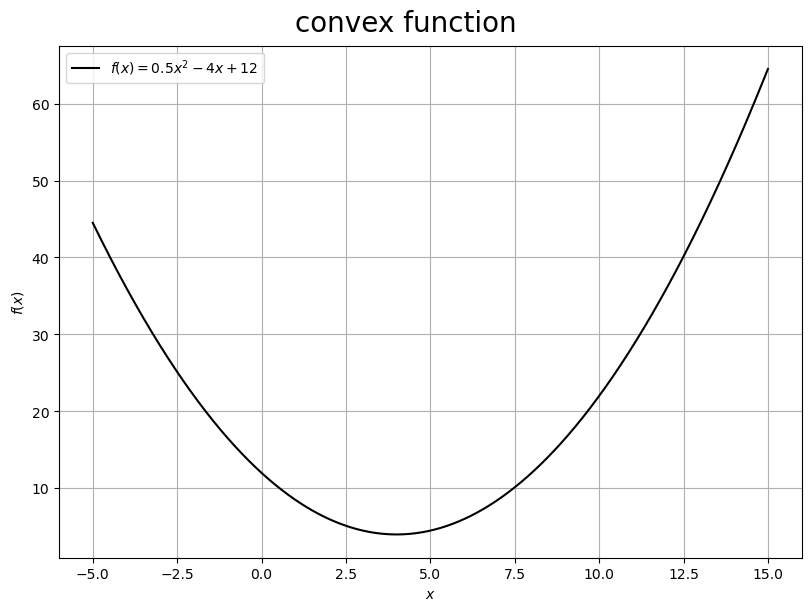
　この関数(曲線) $f(x)$ の最小値となる変数 $x$ を求めます。

　ちなみにこの例の関数の場合は、平方完成により解析的に求まります。

式変形(クリックで展開)

$\displaystyle \begin{aligned} f(x) &= \frac{1}{2} x^2 - 4 x + 12 \\ &= \frac{1}{2} ( x^2 - 8 x ) + 12 \\ &= \frac{1}{2} ( x^2 - 2 \cdot 4 x + 4^2 - 4^2 ) + 12 \\ &= \frac{1}{2} ( x^2 - 2 \cdot 4 x + 4^2 ) - 8 + 12 \\ &= \frac{1}{2} (x - 4)^2 + 4 \end{aligned}$

　 $x = 4$ のとき最小値 $f(x) = 4$ になります。

三分割の図

　次は、三分割の操作を図で示します。

　分割比率を設定します。

# 分割比を指定
r = 1.0 / 3.0
print(r)

0.3333333333333333

　三分探索では、三等分する2つの分割比 $r = \frac{1}{3}$ を用います。

　1回目の試行における分割点を作成します。

# 探索範囲を設定
x_lower = x_min
x_upper = x_max

# 探索範囲を計算
x_size = x_upper - x_lower
print(x_size)

# 分割点を計算
x1 = x_lower + r * x_size
x2 = x_lower + (1.0 - r) * x_size
print(x1)
print(x2)

20.0
1.666666666666666
8.333333333333336

　変数 $x$ の下限を $x_{\mathrm{lower}}$ 、上限を $x_{\mathrm{upper}}$ としたとき、探索範囲のサイズは $x_{\mathrm{upper}} - x_{\mathrm{lower}}$ です。
　探索範囲全体(上限と下限の差)を $1$ として、下限からのサイズ比が $r, (1 - r)$ になるような2点で3分割します。2点は次の式で計算できます。

$\displaystyle \begin{aligned} x_1 &= x_{\mathrm{lower}} + r (x_{\mathrm{upper}} - x_{\mathrm{lower}}) \\ x_2 &= x_{\mathrm{lower}} + (1 - r) (x_{\mathrm{upper}} - x_{\mathrm{lower}}) \end{aligned}$

　分割比が $r \lt 1 - r$ であれば2点は $x_1 \lt x_2$ の関係(図で言うと $x_1$ の点が左側)です。

　1回目の試行における三分割をグラフで確認します。

作図コード(クリックで展開)

# グラフサイズを設定
u = 10
y_max = np.ceil(f_x_vec.max() /u)*u # u単位で切り上げ
y_min = -0.1 * y_max

# 線分の表示位置の調整値を指定
d = 2.0

# ラベル用の文字列を作成
fml_label = f'$r = {r:.3f}, 1-r = {1.0-r:.3f}$'

# 三分割を作図
fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white', 
                       constrained_layout=True)
ax.plot(x_vec, f_x_vec, color='black') # 関数
ax.vlines(x=[x_lower, x_upper], ymin=y_min, ymax=y_max, 
          color='black', linestyle='dashed') # 探索範囲
ax.vlines(x=[x1, x2], ymin=y_min, ymax=y_max, 
          color=['red', 'purple'], linestyle='dashed') # 分割値
ax.hlines(y=0.0, xmin=x_lower, xmax=x_upper, 
          color='black', label='$1$') # 線分 1
ax.hlines(y=[-d, -d*2], xmin=[x_lower, x2], xmax=[x1, x_upper], 
          color='red', label='$r$') # 線分 r
ax.hlines(y=[-d*2, -d], xmin=[x_lower, x1], xmax=[x2, x_upper], 
          color='purple', label='$1-r$') # 線分 1-r
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x)$')
ax.set_title(fml_label, loc='left')
fig.suptitle('ternary section', fontsize=20)
ax.grid()
ax.legend(loc='upper left')
ax.set_ylim(ymin=y_min, ymax=y_max)
plt.show()

　探索範囲における変数 $x$ の下限 $x_{\mathrm{lower}}$ と上限 $x_{\mathrm{upper}}$ を黒色の破線、2つの分割点 $x_1, x_2$ を赤色と紫色の破線で示します。

　探索範囲全体のサイズ( $x_{\mathrm{lower}}$ から $x_{\mathrm{upper}}$ までのサイズ・黒色の実線)を $1$ とすると、 $r \lt (1 - r)$ のとき、下限または上限から小さい(近い)方の分割サイズ( $x_{\mathrm{lower}}$ から $x_1$ までのサイズと $x_{\mathrm{upper}}$ から $x_2$ までのサイズ・赤色の実線)との比が $1 : r$ 、大きい(遠い)方の分割サイズ( $x_{\mathrm{lower}}$ から $x_2$ までのサイズと $x_{\mathrm{upper}}$ から $x_1$ までのサイズ・紫色の実線)との比が $1 : (1 - r)$ になります。
　よって、 $r = \frac{1}{3}$ のとき、各点間のサイズ( $x_{\mathrm{lower}}$ から $x_1$ まで、 $x_1$ から $x_2$ まで、 $x_2$ から $x_{\mathrm{upper}}$ までのサイズ)が等しくなり、探索範囲が三等分されます。

　2回目の試行における分割点を作成します。

# 探索範囲の上限を更新
#x_lower = x1
x_upper = x2

# 探索範囲を計算
x_size = x_upper - x_lower
print(x_size)

# 分割点を計算
x3 = x_lower + r * x_size
x4 = x_lower + (1.0 - r) * x_size
print(x3)
print(x4)

13.333333333333336
-0.5555555555555554
3.888888888888891

　 $x_1 \lt x_2, f(x_1) \gt f(x_2)$ の場合は、下限を $x_1$ に更新 $x_{\mathrm{lower}} \leftarrow x_1$ します。
　 $x_1 \lt x_2, f(x_1) \lt f(x_2)$ の場合は、上限を $x_2$ に更新 $x_{\mathrm{upper}} \leftarrow x_2$ します。この例だと、こちらの操作を行います。
　1試行目と同様に、更新した探索範囲全体を $1$ として、下限からのサイズ比が $r, (1 - r)$ になるような2点で3分割します。2点は先ほどの式で計算できます。

$\displaystyle \begin{aligned} x_3 &= x_{\mathrm{lower}} + r (x_{\mathrm{upper}} - x_{\mathrm{lower}}) \\ x_4 &= x_{\mathrm{lower}} + (1 - r) (x_{\mathrm{upper}} - x_{\mathrm{lower}}) \end{aligned}$

　分割比が $r \lt 1 - r$ であれば2点は $x_3 \lt x_4$ の関係(図で言うと $x_3$ の点が左側)です。

　2回目の試行における黄金分割をグラフで確認します。

作図コード(クリックで展開)

# 線分の表示位置の調整値を指定
d = 2.0

# 三分割を作図
fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white', 
                       constrained_layout=True)
ax.plot(x_vec, f_x_vec, color='black') # 関数
ax.vlines(x=[x_lower, x_upper], ymin=y_min, ymax=y_max, 
          color='black', linestyle='dashed') # 探索範囲
ax.vlines(x=[x3, x4], ymin=y_min, ymax=y_max, 
          color=['blue', 'gold'], linestyle='dashed') # 分割値
ax.hlines(y=0.0, xmin=x_min, xmax=x_max, 
          color='black', label='$1$') # 線分 1
ax.hlines(y=0.0-d, xmin=x_lower, xmax=x_upper, 
          color='purple', label='$1-r$') # 線分 1-r
ax.hlines(y=[-d*2, -d*3], xmin=[x_lower, x4], xmax=[x3, x_upper], 
          color='blue', label='$r (1-r)$') # 線分 r (1-r)
ax.hlines(y=[-d*3, -d*2], xmin=[x_lower, x3], xmax=[x4, x_upper], 
          color='gold', label='$(1-r)^2$') # 線分 (1-r)^2
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x)$')
ax.set_title(fml_label, loc='left')
fig.suptitle('ternary section', fontsize=20)
ax.set_ylim(ymin=y_min, ymax=y_max)
ax.grid()
ax.legend(loc='upper left')
plt.show()

　この試行の探索範囲における変数 $x$ の下限 $x_{\mathrm{lower}}$ と上限 $x_{\mathrm{upper}} = x_2$ を黒色の破線、2つの分割点 $x_3, x_4$ を青色と黄色の破線で示します。

　探索範囲全体のサイズ( $x_{\mathrm{lower}}$ から $x_{\mathrm{upper}}$ までのサイズ・紫色の実線)を $1$ とすると、 $r \lt (1 - r)$ のとき、下限または上限から小さい(近い)方の分割サイズ( $x_{\mathrm{lower}}$ から $x_3$ までのサイズと $x_{\mathrm{upper}}$ から $x_4$ までのサイズ・青色の実線)との比が $1 : r$ 、大きい(遠い)方の分割サイズ( $x_{\mathrm{lower}}$ から $x_4$ までのサイズと $x_{\mathrm{upper}}$ から $x_3$ までのサイズ・黄色の実線)との比が $1 : (1 - r)$ になります。
　よって、 $r = \frac{1}{3}$ のとき、各点間のサイズ( $x_{\mathrm{lower}}$ から $x_3$ まで、 $x_3$ から $x_4$ まで、 $x_4$ から $x_{\mathrm{upper}}$ までのサイズ)が等しくなり、探索範囲が三等分されます。

　元の探索範囲のサイズ(黒色の実線)を $1$ とすると、探索範囲全体のサイズ( $x_{\mathrm{lower}}$ から $x_{\mathrm{upper}}$ までのサイズ・紫色の実線)との比が $1 : (1 - r)$ なので、小さい方の分割サイズとの比が $1 : r (1 - r)$ 、大きい方の分割サイズとの比は $1 : (1 - r)^2$ になります。

　三等分に分割を行いながら探索を行います。

三分探索の図

　続いて、三分探索の操作を図で示します。

　1回目の試行における曲線上の点の座標を作成します。

# 関数値を計算
f_x1 = eval_fnc(x1)
f_x2 = eval_fnc(x2)
print(f_x1)
print(f_x2)

6.722222222222223
13.3888888888889

　2つの分割点 $x_1, x_2$ の関数の値 $f(x_1), f(x_2)$ を計算します。

　1回目の試行における三分探索をグラフで確認します。

作図コード(クリックで展開)

# グラフサイズを設定
u = 10
y_min = 0.0
y_max = np.ceil(f_x_vec.max() /u)*u # u単位で切り上げ

# ラベル用の文字列を作成
fnc_label = f'$f(x_1) = {f_x1:.5f}, f(x_2) = {f_x2:.5f}$'

# 三分探索を作図
fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white', 
                       constrained_layout=True)
ax.plot(x_vec, f_x_vec, color='black') # 関数
ax.vlines(x=[x_min, x_max], ymin=y_min, ymax=y_max, 
          color='black', linestyle='dashed') # 探索範囲
ax.vlines(x=[x1, x2], ymin=y_min, ymax=y_max, 
          color=['red', 'purple'], linestyle='dashed') # 分割値
ax.scatter(x=x1, y=f_x1, 
           s=100, color='red', label='$(x_1, f(x_1))$') # 分割点 1
ax.scatter(x=x2, y=f_x2, 
           s=100, color='purple', label='$(x_2, f(x_2))$') # 分割点 2
ax.hlines(y=[f_x1, f_x2], xmin=x_min, xmax=[x1, x2], 
          color=['red', 'purple'], linestyle='dotted') # 分割点の値
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x)$')
ax.set_title(fnc_label, loc='left')
fig.suptitle('ternary search', fontsize=20)
ax.set_xlim(xmin=x_min, xmax=x_max)
ax.set_ylim(ymin=y_min, ymax=y_max)
ax.grid()
ax.legend(loc='upper left')
plt.show()

　2つの分割点 $x_1, x_2$ に対応する曲線上の点 $(x_1, f(x_1)), (x_2, f(x_2))$ を比較して、小さい方の点を残し、大きい方の点を次の試行の下限または上限(この例だと $x_2$ を上限)とします。

　2回目の試行における曲線上の点の座標を作成します。

# 関数値を計算
f_x3 = eval_fnc(x3)
f_x4 = eval_fnc(x4)
print(f_x3)
print(f_x4)

14.376543209876543
4.006172839506172

　新たな分割点 $x_3, x_4$ の関数の値 $f(x_3), f(x_4)$ を計算します。

　2回目の試行における黄金分割探索をグラフで確認します。

作図コード(クリックで展開)

# ラベル用の文字列を作成
fnc_label = f'$f(x_3) = {f_x3:.5f}, f(x_4) = {f_x4:.5f}$'

# 三分探索を作図
fig, ax = plt.subplots(figsize=(8, 6), dpi=100, facecolor='white', 
                       constrained_layout=True)
ax.plot(x_vec, f_x_vec, color='black') # 関数
ax.vlines(x=[x_lower, x_upper], ymin=y_min, ymax=y_max, 
          color='black', linestyle='dashed') # 探索範囲
ax.vlines(x=[x3, x4], ymin=y_min, ymax=y_max, 
          color=['blue', 'gold'], linestyle='dashed') # 分割値
ax.scatter(x=x3, y=f_x3, 
           s=100, color='blue', label='$(x_3, f(x_3))$') # 分割点 3
ax.scatter(x=x4, y=f_x4, 
           s=100, color='gold', label='$(x_4, f(x_4))$') # 分割点 4
ax.hlines(y=[f_x3, f_x4], xmin=x_min, xmax=[x3, x4], 
          color=['blue', 'gold'], linestyle='dotted') # 分割点の値
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x)$')
ax.set_title(fnc_label, loc='left')
fig.suptitle('ternary search', fontsize=20)
ax.set_xlim(xmin=x_min, xmax=x_max)
ax.set_ylim(ymin=y_min, ymax=y_max)
ax.grid()
ax.legend(loc='upper left')
plt.show()

　1試行目と同様に、2つの分割点 $x_3, x_4$ に対応する曲線上の点 $(x_3, f(x_3)), (x_4, f(x_4))$ を比較して、小さい方の点を残し、大きい方の点を次の試行の下限または上限(この例だと $x_3$ を下限)とします。

　三等分による分割と更新の操作を繰り返すことで、下に凸な関数の最小値を探索します。

探索の推移

　アニメーションの作図コードは「Mathematics/golden_ratio/code/ternary_search.py at main · anemptyarchive/Mathematics · GitHub」を参照してください。

　三分探索の推移をアニメーションで確認します。

　各試行における変数 $x$ の探索範囲の下限 $x_{\mathrm{lower}}$ と上限 $x_{\mathrm{upper}}$ を黒色の破線、分割点 $x_i, x_{i+1}$ をそれぞれ色付きの点と破線で示します。

　試行ごとに、探索範囲を三等分し、 $f(x_i), f(x_{i+1})$ の大きい方の点(変数の値)で下限または上限を更新します。
　この操作を繰り返すことで、変数の範囲を狭めながら最小値の探索を行えます。

　この記事では、三分探索を確認しました。次の記事では、黄金分割探索を確認します。

参考文献

Pythonで学ぶ空間データサイエンス入門: 地域の特徴を発見する方法

作者:植杉　大
Independently published

Amazon

(この本に三分探索は載っていません。この記事を書くきっかけになった黄金分割探索の関連でリンクしています。)

おわりに

　三分割を図で説明する必要があるかというとないのですが、目的の黄金分割探索の記事と同じ構成にして比較するために、こちらの記事でもやっておきました。想定して書き始めたわけではないですが、三等分以外も作図できる(ように対応した)ので、作った甲斐が後から生まれた思われます。
　派生記事の補足記事的に生まれた記事なので、既存カテゴリに該当せず、新たに「アルゴリズム」内の「探索」としたのですが今後このカテゴリの記事は生えるのでしょうか。

【次の内容】

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

【Python】三分探索の可視化

はじめに

三分探索の可視化

関数の設定

三分割の図

三分探索の図

探索の推移

参考文献

おわりに