はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は3.4節「角度」の内容です。
相関係数のグラフを作成します。
【前の内容】
【他の内容】
【今回の内容】
相関係数の可視化
相関係数(correlation coefficient)をグラフで確認します。
相関係数については「3.4:相関係数の計算式【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
要素数を指定して、2つのベクトルを作成します。
# 要素数(次元数)を指定 N = 10 # 混合係数を指定:(-1から1の値) gamma = -0.5 # N個の値(N次元ベクトル)を生成 a = np.random.uniform(low=-10.0, high=10.0, size=N) b_rand = np.random.uniform(low=-10.0, high=10.0, size=N) # 依存関係を設定 b = gamma * a + (1.0 - abs(gamma)) * b_rand print(a[:5].round(2)) print(b[:5].round(2))
[-7.38 2.9 -4.37 4.47 -9.88]
[ 8.54 -0.3 6.06 -0.56 4.28]
次元数を指定して、
次元ベクトル
を
a、を
bとして生成します。ただし、Pythonでは0からインデックスが割り当てられるので、の値は
a[0]に対応します。
np.random.uniform()で一様乱数を生成します。乱数の下限をlow引数、上限をhigh引数、サンプルサイズをsize引数に指定します。
に関する値を
b_randとしておきます。
に依存関係を持たせるために、混合係数
を用いて、
と
を混合します。
のとき負の相関
、
のとき無相関
、
のとき正の相関
になります。
生成したデータを散布図で確認します。
# a,bの散布図を作成 fig, ax = plt.subplots(figsize=(6, 6), facecolor='white') ax.scatter(a, b) # 元データ ax.set_xlabel('$a_i$') ax.set_ylabel('$b_i$') ax.set_title('N=' + str(N), loc='left') fig.suptitle('data a, b', fontsize=20) ax.grid() ax.set_aspect('equal') plt.show()
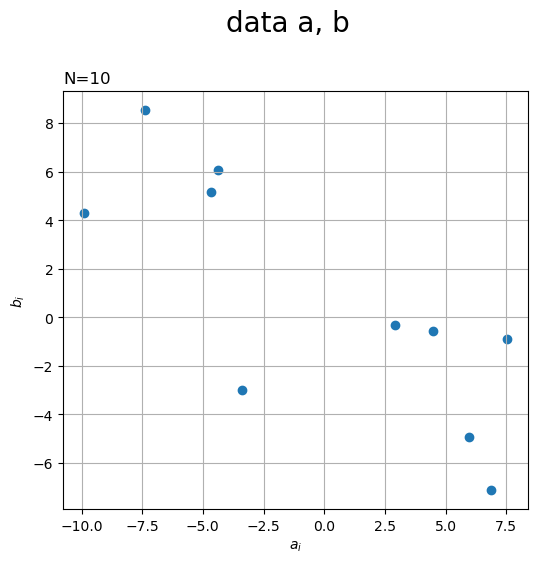
x軸を、y軸を
として、
axes.scatter()で散布図を描画します。
標本平均と標本標準偏差を計算します。
# 平均を計算 avg_a = np.sum(a) / N avg_b = np.sum(b) / N print(avg_a) print(avg_b) # 標準偏差を計算 std_a = np.sqrt(np.sum((a - avg_a)**2) / N) std_b = np.sqrt(np.sum((b - avg_b)**2) / N) print(std_a) print(std_b)
-0.19235475617966546
0.7282306475710945
6.097809201169108
4.845160105918841
それぞれ次の式で計算します。
データを標準化します。
# 標準化 u = (a - avg_a) / std_a v = (b - avg_b) / std_b print(u[:5].round(2)) print(v[:5].round(2))
[-1.18 0.51 -0.69 0.76 -1.59]
[ 1.61 -0.21 1.1 -0.27 0.73]
平均と標準偏差を使って、次の式で標準化します。
標準化したデータを散布図で確認します。
# カラーマップを指定 cm = plt.get_cmap('gist_ncar') # 標準化a,bの散布図を作成 fig, ax = plt.subplots(figsize=(6, 6), facecolor='white') for n in range(N): if n == 0: # 初回のみラベル付け ax.scatter(a[n], b[n], ec=cm(n/N), fc='none', label='$(a_i, b_i)$') # 元データ ax.scatter(u[n], v[n], color=cm(n/N), label='$(u_i, v_i)$') # 標準化データ else: ax.scatter(a[n], b[n], ec=cm(n/N), fc='none') # 元データ ax.scatter(u[n], v[n], color=cm(n/N)) # 標準化データ ax.quiver(a[n], b[n], u[n]-a[n], v[n]-b[n], ec=cm(n/N), fc='none', linewidth=0.5, linestyle=':', scale_units='xy', scale=1, units='dots', width=0.1, headwidth=0.1) # 対応線 ax.set_xlabel('$u_i = \\frac{a_i - avg(a)}{std(a)}$') ax.set_ylabel('$v_i = \\frac{b_i - avg(b)}{std(b)}$') ax.set_title('avg(a)=' + str(avg_a.round(2)) + ', ' + 'std(a)=' + str(std_a.round(2)) + '\n' + 'avg(b)=' + str(avg_b.round(2)) + ', ' + 'std(b)=' + str(std_b.round(2)), loc='left') fig.suptitle('standardization a, b', fontsize=20) ax.grid() ax.legend() ax.set_aspect('equal') plt.show()
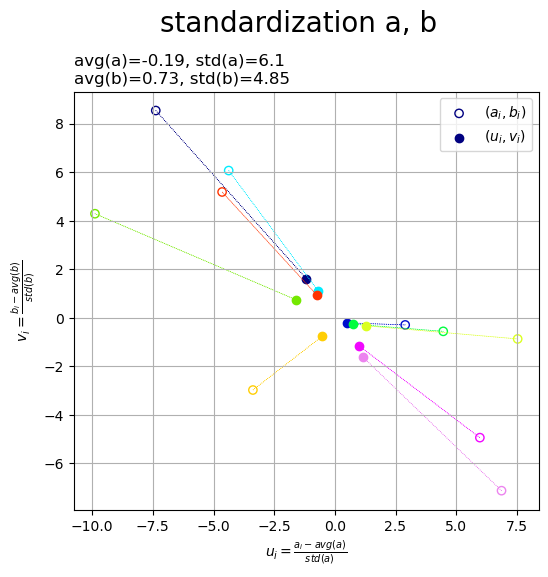
点を白抜きの点、点
を塗りつぶしの点として、散布図を描画します。
標準化によって、各データが原点に近付き、散らばり具合が小さくなるのが分かります。
標本相関係数を計算します。
# 相関係数を計算 dot_ab = np.dot(a-avg_a, b-avg_b) norm_a = np.linalg.norm(a-avg_a) norm_b = np.linalg.norm(b-avg_b) rho = dot_ab / norm_a / norm_b print(rho) # 相関係数を計算 rho = np.dot(u, v) / N print(rho)
-0.7882256538460062
-0.7882256538460058
平均除去ベクトルを用いて、次の式で計算できます。
または、標準化ベクトルを用いて、次の式で計算できます。
値が一致するのを確認できます。
標準化データの散布図に、相関係数の直線を重ねたグラフを作成します。
# グラフサイズ用の値を設定 axis_size = np.max([*abs(u), *abs(v)]) + 1 # 相関係数の直線を作成 x_line = np.linspace(start=-axis_size, stop=axis_size, num=100) y_line = rho * x_line # 相関係数を作図 fig, ax = plt.subplots(figsize=(8, 6), facecolor='white') ax.scatter(u, v) # 標準化a,b ax.plot(x_line, y_line, color='black', label='$y = \\rho x$') # 相関係数 ax.set_xlabel('$\\frac{a_i - avg(a)}{std(a)}$') ax.set_ylabel('$\\frac{b_i - avg(b)}{std(b)}$') ax.set_title('$\\rho=' + str(rho.round(2)) + '$', loc='left') fig.suptitle('correlation coefficient', fontsize=20) ax.grid() ax.legend() ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_aspect('equal') plt.show()
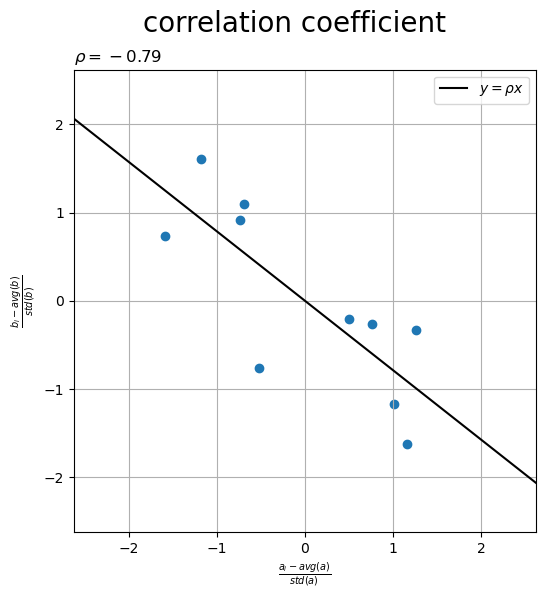
の直線を描画して、相関係数を可視化します。直線が左上がりだと負の相関、水平だと無相関、右上がりだと正の相関を表します。
混合係数の値(相関の強さ)を変化させたアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を設定 frame_num = 101 # 混合係数として利用する値を指定:(-1から1) gamma_vals = np.linspace(start=-1.0, stop=1.0, num=frame_num) # 要素数(次元数)を指定 N = 100 # N個の値(N次元ベクトル)を生成 a = np.random.uniform(low=-10.0, high=10.0, size=N) b_rand = np.random.uniform(low=-10.0, high=10.0, size=N) # 作図用の値を設定 a_max = np.ceil((abs(a).max() - np.mean(a)) / np.std(a)) b_max = np.ceil((abs(b).max() - np.mean(b)) / np.std(b)) axis_size = np.max([a_max, b_max]) + 1 # 作図用のオブジェクトを初期化 fig, ax = plt.subplots(figsize=(8, 8), facecolor='white') fig.suptitle('correlation coefficient', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の混合係数を取得 gamma = gamma_vals[i] # 依存関係を設定 b = gamma * a + (1.0 - abs(gamma)) * b_rand # 平均を計算 avg_a = np.sum(a) / N avg_b = np.sum(b) / N # 標準偏差を計算 std_a = np.sqrt(np.sum((a - avg_a)**2) / N) std_b = np.sqrt(np.sum((b - avg_b)**2) / N) # 標準化 u = (a - avg_a) / std_a v = (b - avg_b) / std_b # 相関係数を計算 rho = np.dot(u, v) / N # 相関係数の直線を作成 x_line = np.linspace(start=-axis_size, stop=axis_size, num=100) y_line = rho * x_line # 相関係数を作図 ax.scatter(u, v) # 標準化a,b ax.plot(x_line, y_line, color='black', label='$y = \\rho x$') # 相関係数 ax.set_xlabel('$\\frac{a_i - avg(a)}{std(a)}$') ax.set_ylabel('$\\frac{b_i - avg(b)}{std(b)}$') ax.set_title('$\\rho=' + str(rho.round(2)) + '$', loc='left') ax.grid() ax.legend(loc='upper left') ax.set_xlim(left=-axis_size, right=axis_size) ax.set_ylim(bottom=-axis_size, top=axis_size) ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('corrd_nd.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。
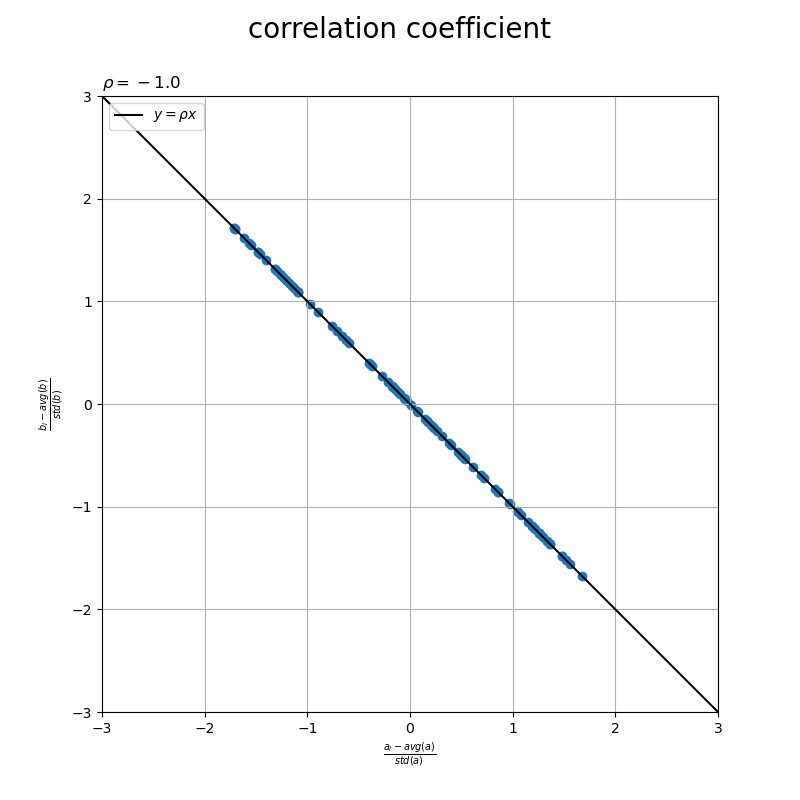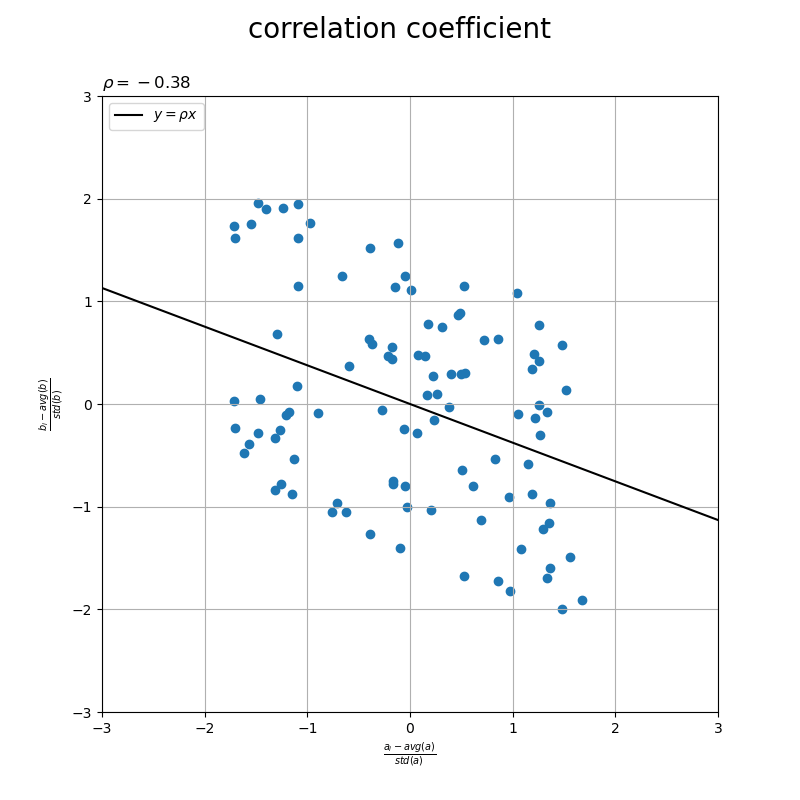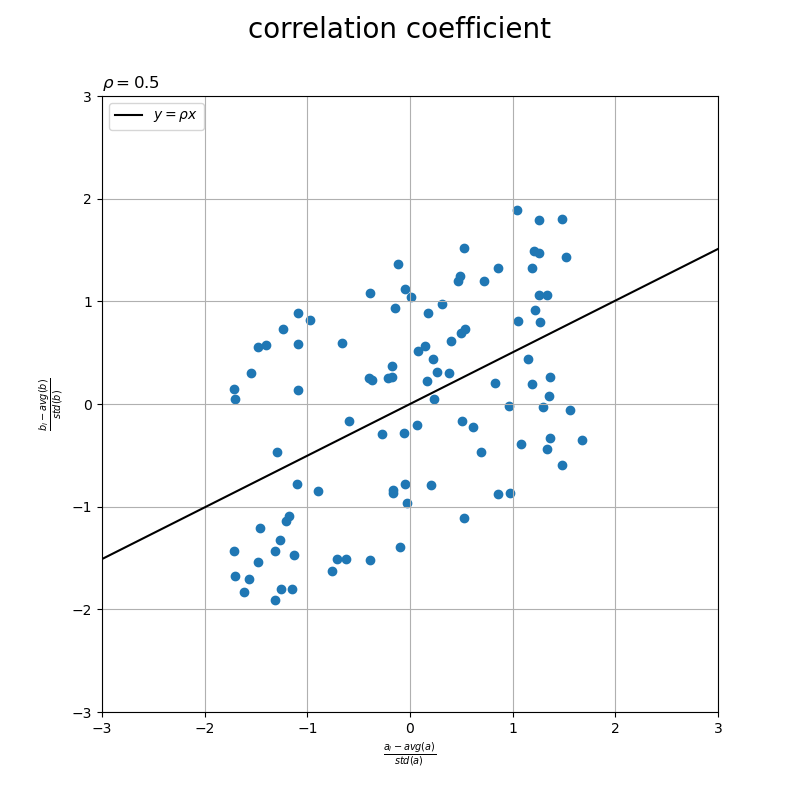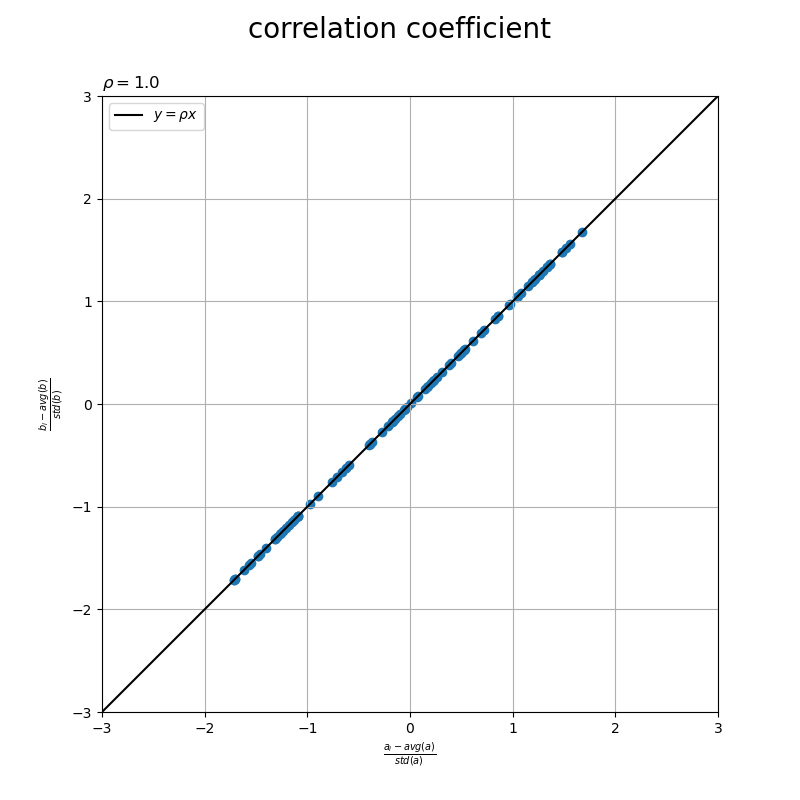
この記事では、相関係数を可視化しました。次の記事では、ベクトルのなす角と相関係数の関係を可視化します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
あれ?相関のあるトイデータってどうやって作るんだと少し悩んだのですが、何とか思い付きました。
【次の内容】