はじめに
『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本の内容を1つずつ確認しながらゆっくりと組んでいきます。
この記事は、8.1.4項「Decoderの改良②」の内容です。Encoderの隠れ状態から必要な情報を抽出するための重みを生成するAttention Weightレイヤの処理を解説して、Pythonで実装します。
【前節の内容】
【他の節の内容】
【この節の内容】
8.1.4 Decoderの改良2
この項では、Attention Weightレイヤを実装します。Attention Weightレイヤは、Encoderの隠れ状態から必要な情報を抽出するための重みを生成します。
# 利用するライブラリ import numpy as np
Attention Weightレイヤの実装には、Softmaxレイヤを利用します。このクラス定義は実装していなかったようなので、次の方法で実装済みのクラスを読み込む必要があります。Softmaxレイヤのクラスは、「common」フォルダ内の「layers.py」ファイルに実装されています。Softmaxレイヤについては、1.3.1項、1巻の3.5節の記事を参照してください。
# 実読み込み用の設定 import sys #sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master') # 実装済みクラスを読み込み from common.layers import Softmax
「deep-learning-from-scratch-2-master」フォルダにパスを設定しておく必要があります。
・処理の確認
図8-15を参考にして、処理を確認していきます。
・内積の確認
まずは、Attention Weightレイヤで利用する内積について確認しておきましょう。内積の計算は、np.dot()で行えます。
# ベクトルを指定 x = np.array([1.0, 1.5, 2.0]) y = np.array([1.4, 1.5, 1.6]) z = np.array([2.0, 3.0, 4.0]) # 内積を計算 print(np.dot(x, y)) print(np.dot(y, z)) print(np.dot(z, x))
6.85
13.7
14.5
ベクトルと内積の関係をグラフで確認しましょう。2次元のグラフにするためベクトルは2次元に設定します。
# 追加ライブラリ import matplotlib.pyplot as plt # ベクトルを指定 a = np.array([1.0, 1.0]) b = np.array([1.0, -1.0]) # 作図 plt.figure(figsize=(9, 9)) # 画像サイズ plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1, color='c', label='a') # 有効グラフ plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1, color='orange', label='b') # 有効グラフ plt.xlim(min(0, a[0], b[0]) - 1, max(0, a[0], b[0]) + 1) plt.ylim(min(0, a[1], b[1]) - 1, max(0, a[1], b[1]) + 1) plt.legend() # 凡例 plt.grid() # 補助線 plt.gca().set_aspect('equal') # アスペクト比 plt.title('a=' + str(a) + ', b=' + str(b) + '$, a \cdot b=$' + str(np.dot(a, b)), fontsize=20, loc='left') plt.show()

ベクトルの向きと内積の関係をアニメーションで確認しましょう。基準となるベクトルをaに、比較するベクトルのサイズをvalに指定します。
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation # 値を指定 val = 2.0 # x軸の値を生成 x_vec = np.linspace(-val, val, num=100, endpoint=False) # ベクトルの座標を計算 point_list = [] for x in x_vec: # x = -val...val, y = val y = np.sqrt(val**2 - x**2) point_list.append([x, y]) for x in reversed(x_vec): #x = val...-val, y = -val y = np.sqrt(val**2 - x**2) point_list.append([x, -y]) # 作図用の関数を定義 def update(i): # 基準となるベクトルを指定 a = [1.0, 1.0] # i番目の座標を取得 b = point_list[i] # 前フレームのグラフを初期化 plt.cla() # 作図 plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1, color='c', label='a') # 有効グラフ plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1, color='orange', label='b') # 有効グラフ plt.xlim(-val - 1.0, val + 1.0) plt.ylim(-val - 1.0, val + 1.0) plt.legend() # 凡例 plt.grid() # グリッド線 plt.gca().set_aspect('equal') # アスペクト比 plt.title('a=' + str(a) + ', b=' + str(list(np.round(b, 2))) + '$, a \cdot b=$' + str(np.round(np.dot(a, b), 3)), fontsize=20, loc='left') # 画像サイズを指定 fig = plt.figure(figsize=(9, 9)) # gif画像を作成 graph = animation.FuncAnimation(fig, update, frames=len(point_list), interval=100) # gif画像を保存 graph.save("dot_graph.gif")
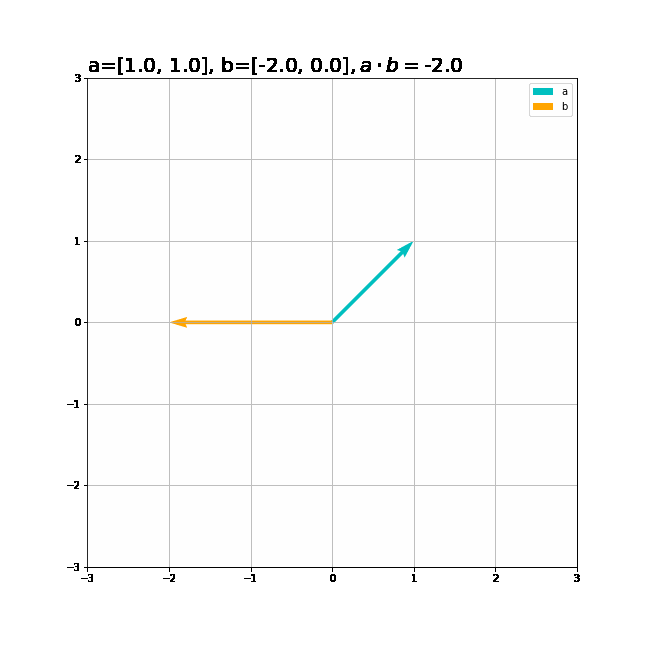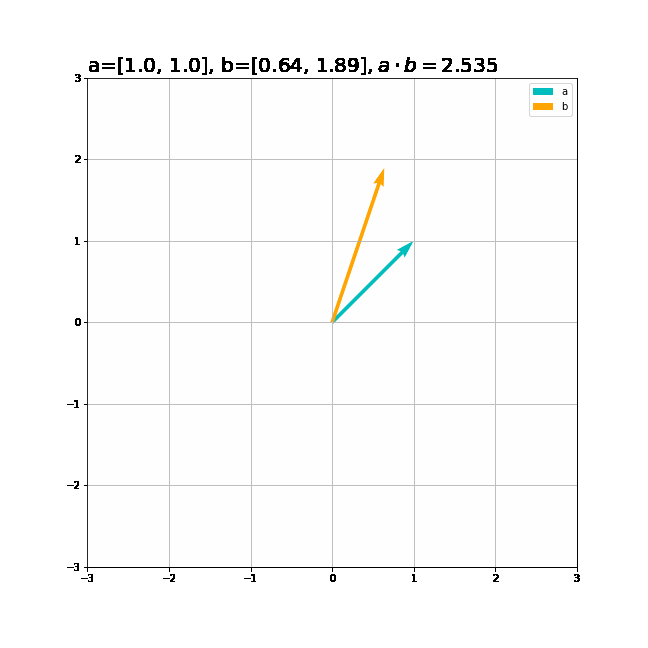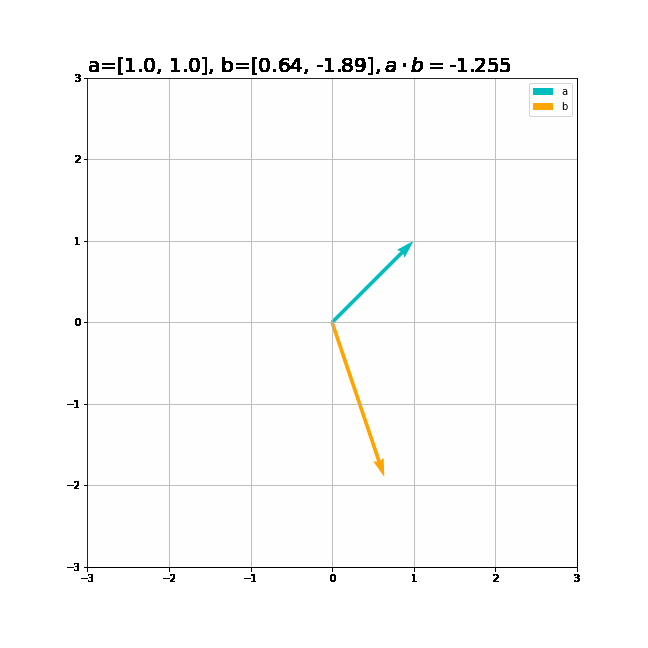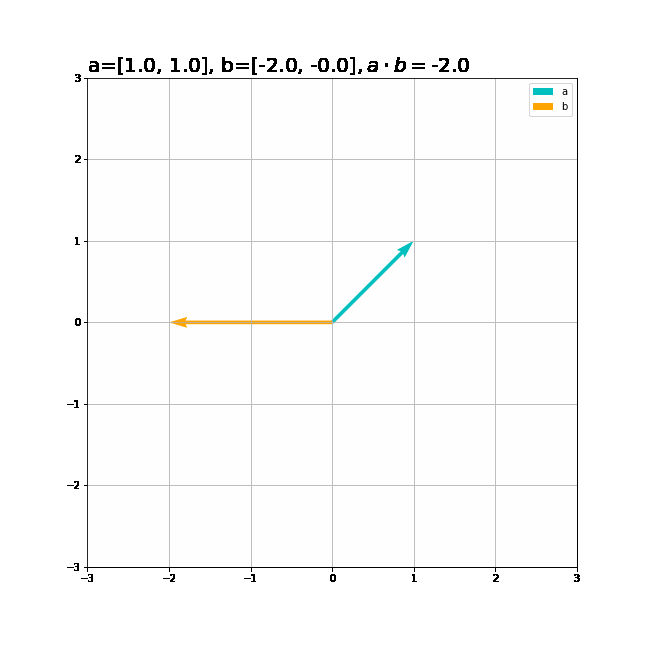
2つのベクトルが同じ方向の内積が最大、逆向きのとき最小、垂直に交わるとき0になるのを確認できます。
では、この内積の性質を利用したDecoderの処理を確認しましょう。
・順伝播の計算
Attention Weightレイヤには、Encoderから隠れ状態$\mathbf{hs}^{(\mathrm{Enc})} = (\mathbf{h}_0^{(\mathrm{Enc})}, \cdots, \mathbf{h}_{T-1}^{(\mathrm{Enc})})$とDecoderの$t$番目のLSTMレイヤから$\mathbf{h}_t^{(\mathrm{Dec})}$が入力します。$\mathbf{hs}^{(\mathrm{Enc})}$の$T$は、Encoder側の時系列サイズです。
データとパラメータの形状に関する値を設定して、$\mathbf{hs}^{(\mathrm{Enc})}$と$\mathbf{h}_t^{(\mathrm{Dec})}$を処理結果が分かりやすくなるように作成しておきます。また、正規化用にSoftmaxレイヤのインスタンスも作成します。
# データとパラメータの形状に関する値を指定 N = 3 # バッチサイズ(入力する文章数) T = 4 # Encoderの時系列サイズ(入力する単語数) H = 5 # 隠れ状態のサイズ(LSTMレイヤの中間層のニューロン数) # (簡易的に)EncoderのT個の隠れ状態を作成 hs = np.arange(N * T * H).reshape((N, T, H)) + 1 print(hs) print(hs.shape) # (簡易的に)Decoderのt番目の隠れ状態を作成 h = np.arange(N * H).reshape((N, H)) + 1 print(h) print(h.shape) # Softmaxレイヤのインスタンスを作成 softmax_layer = Softmax()
[[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]
[16 17 18 19 20]]
[[21 22 23 24 25]
[26 27 28 29 30]
[31 32 33 34 35]
[36 37 38 39 40]]
[[41 42 43 44 45]
[46 47 48 49 50]
[51 52 53 54 55]
[56 57 58 59 60]]]
(3, 4, 5)
[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]]
(3, 5)
この章では、NumPy配列の表示形式に合わせて配列を表記することにします。$\mathbf{hs}^{(\mathrm{Enc})}$は、$(N \times T \times H)$の3次元配列
です。各列(2次元方向に並ぶ$H$個の要素)は隠れ状態ベクトルの次元を、各行(1次元方向に並ぶ$T$個の要素)は時刻を表します。また、$T$行$H$列のまとまりで横(NumPy配列の出力としては縦)に並ぶ要素が、0次元方向に並ぶ$N$個の要素で、何番目のバッチデータなのかを表します。例えば、$(h_{0,0,0}, \cdots, h_{0,0,H-1})$は0番目のバッチデータにおける時刻0の隠れ状態ベクトルです。
$\mathbf{h}_t^{(\mathrm{Dec})}$は、$N \times H$の2次元配列
です。
(各要素にまで${(\mathrm{Enc})}$や${(\mathrm{Dec})}$を付けるとごちゃごちゃするので極力省略します。)
ブロードキャスト等の機能を使わず明示的に計算を行うために、$\mathbf{hs}^{(\mathrm{Enc})}$と$\mathbf{h}_t^{(\mathrm{Dec})}$の形状を一致させます。$\mathbf{h}_t^{(\mathrm{Dec})}$を要素数はそのまま3次元配列に変換します。
# 3次元配列に変換 tmp_h = h.reshape((N, 1, H)) print(tmp_h) print(tmp_h.shape)
[[[ 1 2 3 4 5]]
[[ 6 7 8 9 10]]
[[11 12 13 14 15]]]
(3, 1, 5)
$(N \times 1 \times H)$の3次元配列
となりました。
$\mathbf{h}_t^{(\mathrm{Dec})}$を時系列方向(0から数えて1次元方向)に$T$個複製して、$\mathbf{hr}^{(\mathrm{Dec})} = (\underbrace{ \mathbf{h}_t^{(\mathrm{Dec})}, \cdots, \mathbf{h}_t^{(\mathrm{Dec})} }_{T})$とします(リシェイプのrかも?)。
# Decoderのt番目の隠れ状態を複製 hr = tmp_h.repeat(T, axis=1) print(hr) print(hr.shape)
[[[ 1 2 3 4 5]
[ 1 2 3 4 5]
[ 1 2 3 4 5]
[ 1 2 3 4 5]]
[[ 6 7 8 9 10]
[ 6 7 8 9 10]
[ 6 7 8 9 10]
[ 6 7 8 9 10]]
[[11 12 13 14 15]
[11 12 13 14 15]
[11 12 13 14 15]
[11 12 13 14 15]]]
(3, 4, 5)
$\mathbf{hr}^{(\mathrm{Dec})}$は、$(N \times T \times H)$の3次元配列
です。$\mathbf{hs}^{(\mathrm{Enc})}$と同じ形状になりました。
「Encoderの隠れ状態$\mathbf{hs}^{(\mathrm{Enc})}$」と「複製したDecoderの隠れ状態$\mathbf{hr}^{(\mathrm{Dec})}$」を要素ごとに掛けます。計算結果を$\mathbf{t}$とします(何由来のtか分からない、tmp?時間インデックスの$t$とは別物です)。
# 乗算ノードの順伝播を計算 t = hs * hr print(t) print(t.shape)
[[[ 1 4 9 16 25]
[ 6 14 24 36 50]
[ 11 24 39 56 75]
[ 16 34 54 76 100]]
[[126 154 184 216 250]
[156 189 224 261 300]
[186 224 264 306 350]
[216 259 304 351 400]]
[[451 504 559 616 675]
[506 564 624 686 750]
[561 624 689 756 825]
[616 684 754 826 900]]]
(3, 4, 5)
要素ごとの積はアダマール積と呼び、$\odot$を使って(行列の積と区別できるように)表します。同じ形状の配列を要素ごとに掛けただけなので、形状は変わらず$(N \times T \times H)$の3次元配列
です。以降の計算を分かりやすくするために、$\mathbf{t}$の要素を$t_{n,t,h} = h_{n,t,h}^{(\mathrm{Enc})} h_{n,t',h}^{(\mathrm{Dec})}$で表すことにします。ただし、$t$はEncoderの時刻インデックスであり0から$T-1$の値をとり、$t'$はDecoderの時刻インデックスであり固定された値です。
$\mathbf{t}$について(0から数えて)2次元方向に和をとって、スコア$\mathbf{s}$とします(スコアのsですね)。
# スコアを計算 s = np.sum(t, axis=2) print(s) print(s.shape)
[[ 55 130 205 280]
[ 930 1130 1330 1530]
[2805 3130 3455 3780]]
(3, 4)
$\mathbf{s}$は、$(N \times T)$の2次元配列
です。また、$s_{n,t} = \sum_{h=0}^{H-1} t_{n,t,h} = \sum_{h=0}^{H-1} h_{n,t,h}^{(\mathrm{Enc})} h_{n,t',h}^{(\mathrm{Dec})}$です。
Softmax関数により時系列方向(行方向)の和が1になるように正規化して、Attentionの重み$\mathbf{a}$とします(Attentionのaですかね、NNで出てくるアクティベーションのaとは別物だと思います)。
# 重みに変換(正規化) a = softmax_layer.forward(s) print(np.round(a, 2)) print(np.sum(a, axis=1)) print(a.shape)
[[0. 0. 0. 1.]
[0. 0. 0. 1.]
[0. 0. 0. 1.]]
[1. 1. 1.]
(3, 4)
正規化しただけなので形状は変わらず、$(N \times T)$の2次元配列
です。文章ごとの和が1になります。
$\mathbf{a}$は、同じ時刻の前項で実装したWeight Sumレイヤに入力します。
以上が順伝播の処理です。続いて、逆伝播の処理を確認します。
・逆伝播の計算
Weight SumレイヤからAttentionの重みの勾配$\frac{\partial L}{\partial \mathbf{a}}$が入力します。ここではこれを簡易的に作成します。
# (簡易的に)逆伝播の入力を作成 da = np.random.randn(N, T) print(da) print(da.shape)
[[-0.98521478 -0.86732955 0.84286631 -0.93588282]
[ 0.66773016 0.23237067 1.89309376 -0.26321849]
[ 0.48920449 1.17508848 0.54026007 -0.66672641]]
(3, 4)
$\frac{\partial L}{\partial \mathbf{a}}$は、$(N \times T)$の2次元配列
で、$\mathbf{a}$と同じ形状です。
Softmaxレイヤの逆伝播を計算して、スコアの勾配を$\frac{\partial L}{\partial \mathbf{s}}$求めます。
# Softmaxレイヤの逆伝播(スコアの勾配)を計算 ds = softmax_layer.backward(da) print(ds) print(ds.shape)
[[-9.48134503e-100 4.91876329e-067 4.76462316e-033 0.00000000e+000]
[ 2.46738307e-261 9.49137294e-175 2.98411303e-087 0.00000000e+000]
[ 0.00000000e+000 9.41526921e-283 8.62970175e-142 0.00000000e+000]]
(3, 4)
$\frac{\partial L}{\partial \mathbf{s}}$は、$(N \times T)$の2次元配列
で、$\mathbf{s}$と同じ形状です。Softmax関数の逆伝播については、1巻の5.6.3項を参照してください。
$\mathbf{t}$から$\mathbf{s}$への順伝播の計算では、(0から数えて)2次元方向に和をとりました。和の計算はSumノードです。Sumノードの逆伝播では、(要素数は同じまま3次元配列に変換した上で)時系列方向に要素を$H$個複製します(1.3.4.4項「Sumノード」)。
ここからの処理がややこしいので、スコアの勾配dsを処理結果が分かりやすいように作り直しましょう。
# (簡易的に)スコアの勾配を作成 ds = np.arange(N * T).reshape(N, T) print(ds) print(ds.shape) # Sumノードの逆伝播を計算 dt = ds.reshape((N, T, 1)).repeat(H, axis=2) print(dt) print(dt.shape)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
(3, 4)
[[[ 0 0 0 0 0]
[ 1 1 1 1 1]
[ 2 2 2 2 2]
[ 3 3 3 3 3]]
[[ 4 4 4 4 4]
[ 5 5 5 5 5]
[ 6 6 6 6 6]
[ 7 7 7 7 7]]
[[ 8 8 8 8 8]
[ 9 9 9 9 9]
[10 10 10 10 10]
[11 11 11 11 11]]]
(3, 4, 5)
計算結果は、$\mathbf{t}$の勾配$\frac{\partial L}{\partial \mathbf{t}}$です。$\frac{\partial L}{\partial \mathbf{t}}$は、$(N \times T \times H)$の3次元配列
で、$\mathbf{t}$と同じ形状です。また、$\frac{\partial L}{\partial t_{n,t,h}} = \frac{\partial L}{\partial s_{n,t}}$です。
$\mathbf{t}$(の各要素)を求める順伝播の計算は乗算ノードです。乗算ノードの逆伝播を計算します(1.3.4.1項「乗算ノード」)。
# 乗算ノードの逆伝播を計算 dhs = dt * hr # EncoderのT個の隠れ状態の勾配 print(dhs) print(dhs.shape)
[[[ 0 0 0 0 0]
[ 1 2 3 4 5]
[ 2 4 6 8 10]
[ 3 6 9 12 15]]
[[ 24 28 32 36 40]
[ 30 35 40 45 50]
[ 36 42 48 54 60]
[ 42 49 56 63 70]]
[[ 88 96 104 112 120]
[ 99 108 117 126 135]
[110 120 130 140 150]
[121 132 143 154 165]]]
(3, 4, 5)
計算結果は、Encoderの隠れ状態の勾配$\frac{\partial L}{\partial \mathbf{hs}^{(\mathrm{Enc})}}$です。$\frac{\partial L}{\partial \mathbf{hs}^{(\mathrm{Enc})}}$は、$(N \times T \times H)$の3次元配列
で、$\mathbf{hs}^{(\mathrm{Enc})}$と同じ形状です。また、$\frac{\partial L}{\partial h_{n,t,h}^{(\mathrm{Enc})}} = \frac{\partial L}{\partial t_{n,t,h}} h_{n,t',h}^{(\mathrm{Dec})}$です。ただし、$t$はEncoderの時刻インデックスであり0から$T-1$の値をとり、$t'$はDecoderの時刻インデックスであり固定された値です。
同様に、もう1つの変数も計算します。
# 乗算ノードの逆伝播を計算 dhr = dt * hs print(dhr) print(dhr.shape)
[[[ 0 0 0 0 0]
[ 6 7 8 9 10]
[ 22 24 26 28 30]
[ 48 51 54 57 60]]
[[ 84 88 92 96 100]
[130 135 140 145 150]
[186 192 198 204 210]
[252 259 266 273 280]]
[[328 336 344 352 360]
[414 423 432 441 450]
[510 520 530 540 550]
[616 627 638 649 660]]]
(3, 4, 5)
計算結果は、複製したDecoderの隠れ状態の勾配$\frac{\partial L}{\partial \mathbf{hr}^{(\mathrm{Dec})}}$です。$\frac{\partial L}{\partial \mathbf{hr}^{(\mathrm{Dec})}}$は、$(N \times T \times H)$の3次元配列
で、$\mathbf{hr}^{(\mathrm{Dec})}$と同じ形状です。また、$\frac{\partial L}{\partial h_{n,t',h}^{(\mathrm{Dec})}} = \frac{\partial L}{\partial t_{n,t,h}} h_{n,t,h}^{(\mathrm{Enc})}$です。
$\mathbf{h}_t^{(\mathrm{Dec})}$から$\mathbf{hr}^{(\mathrm{Dec})}$への順伝播では、時系列方向に要素を$T$個複製しました。これはRepeatノードです。Repeatノードの逆伝播では、分岐した$T$個の要素の和をとります。
# Repeatノードの逆伝播を計算 dh = np.sum(dhr, axis=1) # Decoderのt番目の隠れ状態の勾配 print(dh) print(dh.shape)
[[ 76 82 88 94 100]
[ 652 674 696 718 740]
[1868 1906 1944 1982 2020]]
(3, 5)
計算結果は、Decoderの$t$番目の隠れ状態の勾配$\frac{\partial L}{\partial \mathbf{h}_t^{(\mathrm{Dec})}}$です。$\frac{\partial L}{\partial \mathbf{h}_t^{(\mathrm{Dec})}}$は、$(N \times H)$の2次元配列
で、$\mathbf{h}_t^{(\mathrm{Dec})}$と同じ形状です。また、$ \frac{\partial L}{\partial h_{n,h}^{(t)}} = \sum_t \frac{\partial L}{\partial h_{n,t,h}^{(\mathrm{Dec})}}$です。
$\frac{\partial L}{\partial \mathbf{h}_t^{(\mathrm{Dec})}}$は、Decoderの$t$番目のLSTMレイヤに入力します。
以上がAttention Weightレイヤで行う処理です。
・実装
処理の確認ができたので、Attention Weightレイヤをクラスとして実装します。
# Attention Weightレイヤの実装 class AttentionWeight: # 初期化メソッド def __init__(self): # 他のレイヤと対応させるための空のリストを作成 self.params = [] # パラメータ self.grads = [] # 勾配 # Softmaxレイヤのインスタンスを作成 self.softmax = Softmax() # 中間変数の受け皿を初期化 self.cache = None # 順伝播メソッド def forward(self, hs, h): # 変数の形状に関する値を取得 N, T, H = hs.shape # Encoderの隠れ状態同じ形状に複製 hr = h.reshape((N, 1, H)).repeat(T, axis=1) # スコア(内積)を計算 t = hs * hr s = np.sum(t, axis=2) # Attentionの重みに変換(正規化) a = self.softmax.forward(s) # 逆伝播の計算用に変数を保存 self.cache = (hs, hr) return a # 逆伝播メソッド def backward(self, da): # 変数を取得 hs, hr = self.cache # 形状に関する値を取得 N, T, H = hs.shape # Softmaxレイヤの逆伝播(スコアの勾配)を計算 ds = self.softmax.backward(da) # Sumノードの逆伝播を計算 dt = ds.reshape((N, T, 1)).repeat(H, axis=2) # 乗算ノードの逆伝播を計算 dhs = dt * hr # EncoderのT個の隠れ状態の勾配 dhr = dt * hs # Repeatノードの逆伝播を計算 dh = np.sum(dhr, axis=1) # Decoderのt番目の隠れ状態の勾配 return dhs, dh
実装したクラスを試してみましょう。
Encoderの隠れ状態$\mathbf{hs}$とDecoderの隠れ状態$\mathbf{h}_t$を簡易的に作成して、Attention Weightレイヤのインスタンスを作成します。
# (簡易的に)EncoderのT個の隠れ状態を作成 hs = np.random.randn(N, T, H) print(hs.shape) # (簡易的に)Decoderの隠れ状態を作成 h = np.random.randn(N, H) print(h.shape) # インスタンスを作成 attention_weight_layer = AttentionWeight()
(3, 4, 5)
(3, 5)
順伝播を計算します。
# 順伝播を計算 a = attention_weight_layer.forward(hs, h) print(np.round(a, 2)) print(np.sum(a, axis=1)) print(a.shape)
[[0.47 0. 0.53 0. ]
[0.16 0. 0.81 0.03]
[0. 0.94 0.03 0.02]]
[1. 1. 1.]
(3, 4)
aの各行の和をとると1になるのを確認できました。aを前項で実装したWeight Sumレイヤに入力します。
Attentionの重みの勾配(Weight Sumレイヤの出力)$\frac{\partial L}{\partial \mathbf{a}}$を簡易的に作成して、逆伝播を計算します。
# (簡易的に)逆伝播の入力を作成 da = np.random.randn(N, T) print(da.shape) # 逆伝播を計算 dhs, dh = attention_weight_layer.backward(da) print(np.round(dhs, 3)) print(dhs.shape) print(np.round(dh, 3)) print(dh.shape)
(3, 4)
[[[ 6.900e-02 1.542e+00 3.880e-01 -6.280e-01 2.230e-01]
[ 0.000e+00 1.000e-03 0.000e+00 -0.000e+00 0.000e+00]
[-6.900e-02 -1.543e+00 -3.880e-01 6.280e-01 -2.230e-01]
[ 0.000e+00 0.000e+00 0.000e+00 -0.000e+00 0.000e+00]]
[[ 2.240e-01 1.730e-01 -1.500e-01 5.600e-02 -3.230e-01]
[ 5.000e-03 4.000e-03 -3.000e-03 1.000e-03 -7.000e-03]
[-1.670e-01 -1.290e-01 1.120e-01 -4.200e-02 2.410e-01]
[-6.200e-02 -4.800e-02 4.100e-02 -1.600e-02 8.900e-02]]
[[ 1.000e-03 -0.000e+00 -2.000e-03 2.000e-03 -0.000e+00]
[-1.700e-02 3.000e-03 5.400e-02 -6.500e-02 7.000e-03]
[ 1.000e-03 -0.000e+00 -4.000e-03 5.000e-03 -1.000e-03]
[ 1.500e-02 -2.000e-03 -4.800e-02 5.800e-02 -6.000e-03]]]
(3, 4, 5)
[[-1.191 -0.152 -0.155 -0.276 0.675]
[-0.082 -0.04 0.089 -0.061 0.07 ]
[-0.131 0.02 -0.003 -0.046 -0.021]]
(3, 5)
dhsはEncoderのTime LSTMレイヤに、dhはDecoderの同じ時刻のLSTMレイヤに入力します。
以上でAttentioレイヤで用いるAttention WeightレイヤとWeight Sumレイヤを実装できました。次項では、Attentionレイヤを実装します。
参考文献
おわりに
前項とこの項はえらくごちゃごちゃして読みにくいですね。書くのも大変でした。悩みながら書いた文章って読みにくいんだと最近分かりました。悩み自体は解決して私はスッキリしてるんですが。それとは別に、数式が多くなるとJupyterLabが重くなるのが厄介です。
【次節の内容】
