1.1.11：ラグランジュの未定乗数法【『トピックモデル』の勉強ノート】

はじめに

　機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に自分の理解の助けになったことや勉強会資料のまとめです。トピックモデルの各種アルゴリズムを「数式」と「プログラム」から理解することを目指します。

　この記事は、1.1.10項「ラグランジュの未定乗数法」の内容です。ラグランジュの未定乗数法を定義と簡単な例題で説明します。

【前節の内容】

www.anarchive-beta.com

【他の節一覧】

www.anarchive-beta.com

【この節の内容】

はじめに
1.1.11 ラグランジュの未定乗数法
- ・例題
参考書籍
おわりに

1.1.11 ラグランジュの未定乗数法

　ラグランジュの未定乗数法を用いると、ある関数の最大値・最小値を制約条件の下で求めることができる。(よく分からない(未定の)値$\lambda$を制約条件の式に掛ける(乗数とする)ことで、制約付きの最適化問題を簡単に解くことができる、というラグランジュさんが考えた方法)

　$f(\boldsymbol{\phi})$を最大化する$\boldsymbol{\phi}$を求める。ただし、$I$個の制約$g_i(\boldsymbol{\phi}) = 0,\ i = 1, 2, \cdots, I$があるとする。このような問題を等式制約付き最適化問題といい、ラグランジュの未定乗数法を用いて解くことができる。(要は$g$の式を満たす範囲で$f$の式が最大化する値を求めるということ。そして、ラグランジュの未定乗数法を使うと簡単に解けてしまう。)

$$ \max_{\boldsymbol{\phi}} f(\boldsymbol{\phi}),\ \boldsymbol{\phi} = (\phi_1, \phi_2, \cdots, \phi_v),\ \quad \text{ただし} \quad g_i(\boldsymbol{\phi}) = 0,\ i = 1, 2, \cdots, I $$

　未定の$\boldsymbol{\lambda} = (\lambda_1, \cdots, \lambda_I$)を制約関数$g_i(\boldsymbol{\phi})$の乗数として$L(\boldsymbol{\phi}, \boldsymbol{\lambda})$を作る。(かなりざっくりいうと$f(\boldsymbol{\phi})$と制約曲線$g_i(\boldsymbol{\phi})$との接点(等しい点)を見付ける感じの操作。つまり$f(\boldsymbol{\phi})=\lambda_i g_i(\phi)$となるような関数$F(\boldsymbol{\phi}, \boldsymbol{\lambda})$を新たに作る(ラグランジュなのでL)。ちなみに交点も等しい点なのだが、極値ではない)
　条件が複数ある場合には、全ての条件の和をとる。

$$ L(\boldsymbol{\phi}, \boldsymbol{\lambda}) = f(\boldsymbol{\phi}) + \sum_{i=1}^I \lambda_i g_i(\boldsymbol{\phi}) $$

　この式を偏微分して0となる$\boldsymbol{\phi}$のとき、制約を満たす範囲内で$f(\boldsymbol{\phi})$は最大となる。

$$ \frac{ \partial L(\boldsymbol{\phi}) }{ \partial \boldsymbol{\phi} } = 0, \ \frac{ \partial L(\boldsymbol{\lambda}) }{ \partial \boldsymbol{\lambda} } = 0 $$

・例題

　簡単な例として、長方形の面積の最大化について考える。長方形の2辺$x,\ y$の合計が10としたとき、長方形の面積が最大となる$x, y$を求めるとする。つまり、制約$g(x, y) = 10$の下で面積$f(x, y)$を最大化する2辺$x,\ y$を、ラグランジュの未定乗数法を用いて求める。

　それぞれの関数は

$$ f(x, y) = xy,\ g(x, y) = x + y = 10 $$

である。これに未定乗数$\lambda$を使って、$L(x, y, \lambda)$を立てる。

$$ L(x, y, \lambda) = x y + \lambda(x + y - 10) \\ $$

　この式を各変数について偏微分して0になる値を求める。偏微分とは、複数の変数を持つ関数を微分する際に、他の変数は定数として扱い1つの変数のみを微分すること。

　まずは、$x$の項に関して式を整理し

$$ \begin{aligned} L(x, y, \lambda) &= x y + \lambda(x + y - 10) \\ &= (y + \lambda) x + (\lambda y - 10 \lambda) \\ \end{aligned} $$

　この式を$x$で微分して0とおく。

$$ \frac{\partial L}{\partial x} = y + \lambda = 0 \tag{1} $$

　次に、$y$についても同様に式を整理して

$$ \begin{aligned} L(x, y, \lambda) &= x y + \lambda(x + y - 10) \\ &= (x + \lambda) y + (\lambda x - 10 \lambda) \\ \end{aligned} $$

この式を$y$に関して微分して0とおく。

$$ \frac{\partial L}{\partial y} = x + \lambda = 0 \tag{2} $$

　最後に、$\lambda$の項は既にまとまっているので、そのまま微分して0とおく。

$$ \frac{\partial L}{\partial \lambda} = x + y - 10 = 0 \tag{3} $$

　(1)、(2)、(3)の連立方程式を解くと

$$ x = 5,\ y = 5,\ \lambda = -5 $$

が求まる。

　$g(x, y) = x + y = 10$の制約を満たす面積の最大値は$f(x, y) = x y = 25$であり、またそのときの2辺は$x = y = 5$であることが分かった。

　続いて、ラグランジュの未定乗数法をグラフでも確認していく。まずは、2辺の値と面積の関係をみる。

# 利用パッケージ
library(tidyverse)

# 面積のデータフレームを作成
f_xy <- tibble(
  x = rep(seq(0, 10, 0.1), 101), 
  y = rep(seq(0, 10, 0.1), each = 101), 
  z = x * y
)

# 辺と面積の関係を可視化(ヒートマップ)
ggplot(data = f_xy, mapping = aes(x = x, y = y, fill = z)) + # データ
  geom_tile() + # ヒートマップ
  scale_fill_gradientn(colors = c("blue", "green", "yellow", "orange")) + # タイルの色
  coord_fixed(ratio = 1) # 縦横比

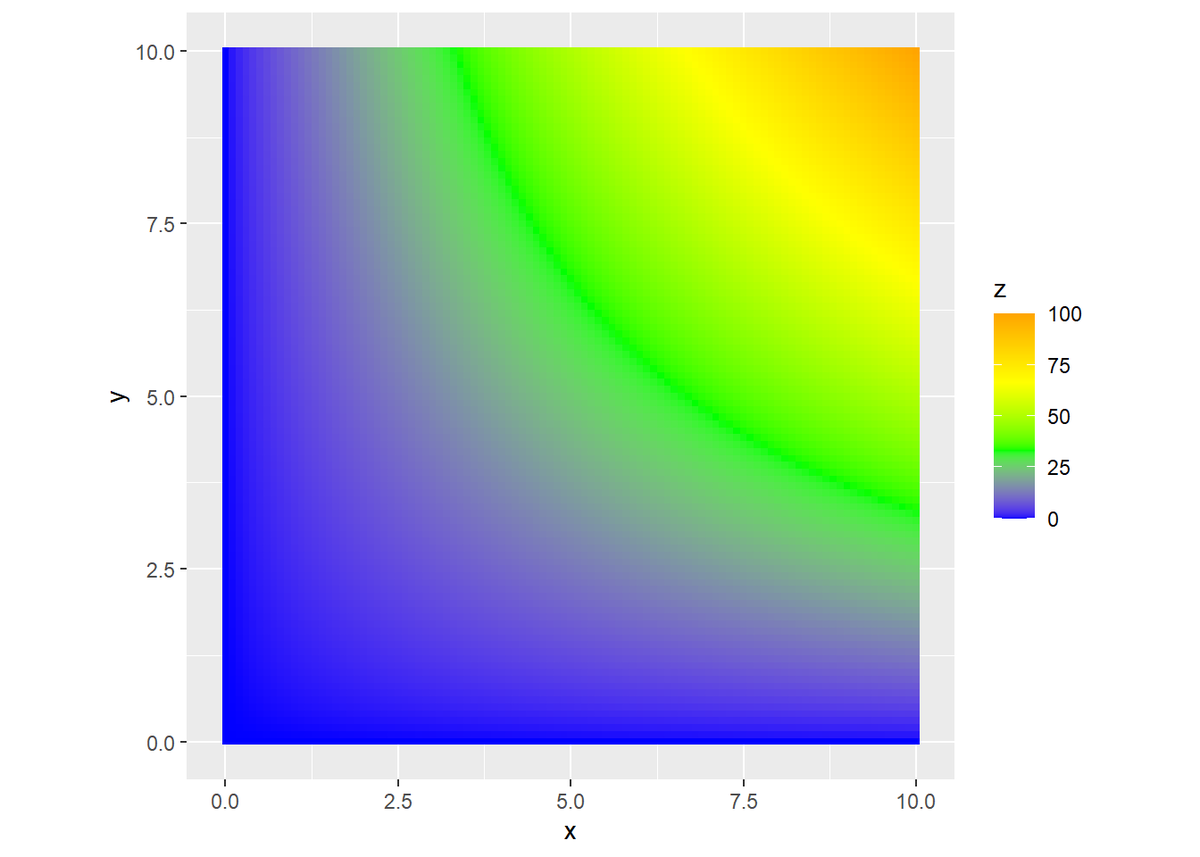
　長方形の2辺をx軸、y軸とし、面積をzとしている。面積zの値が大きくなるほど、色が青からオレンジになる(各辺を縦横、面積を高さとした三次元のグラフの代用)。

　このままでは制約との関係が分かりにくいため、面積$f(x, y) = z$が等しい2辺の組み合わせを結ぶ曲線を5刻みで引く。

# 辺と面積の関係を可視化(等高線)
ggplot(data = f_xy, mapping = aes(x = x, y = y, z = z)) + # データ
  geom_tile(aes(fill = z), alpha = 0.5) + # ヒートマップ
  scale_fill_gradientn(colors = c("blue", "green", "yellow", "orange")) + # タイルの色
  geom_contour(aes(color = stat(level)), binwidth = 5, size = 1) + # 等高線
  scale_color_gradientn(colors = c("blue", "green", "yellow", "orange")) + # 線の色
  guides(color = FALSE) + # 凡例
  coord_fixed(ratio = 1) # 縦横比

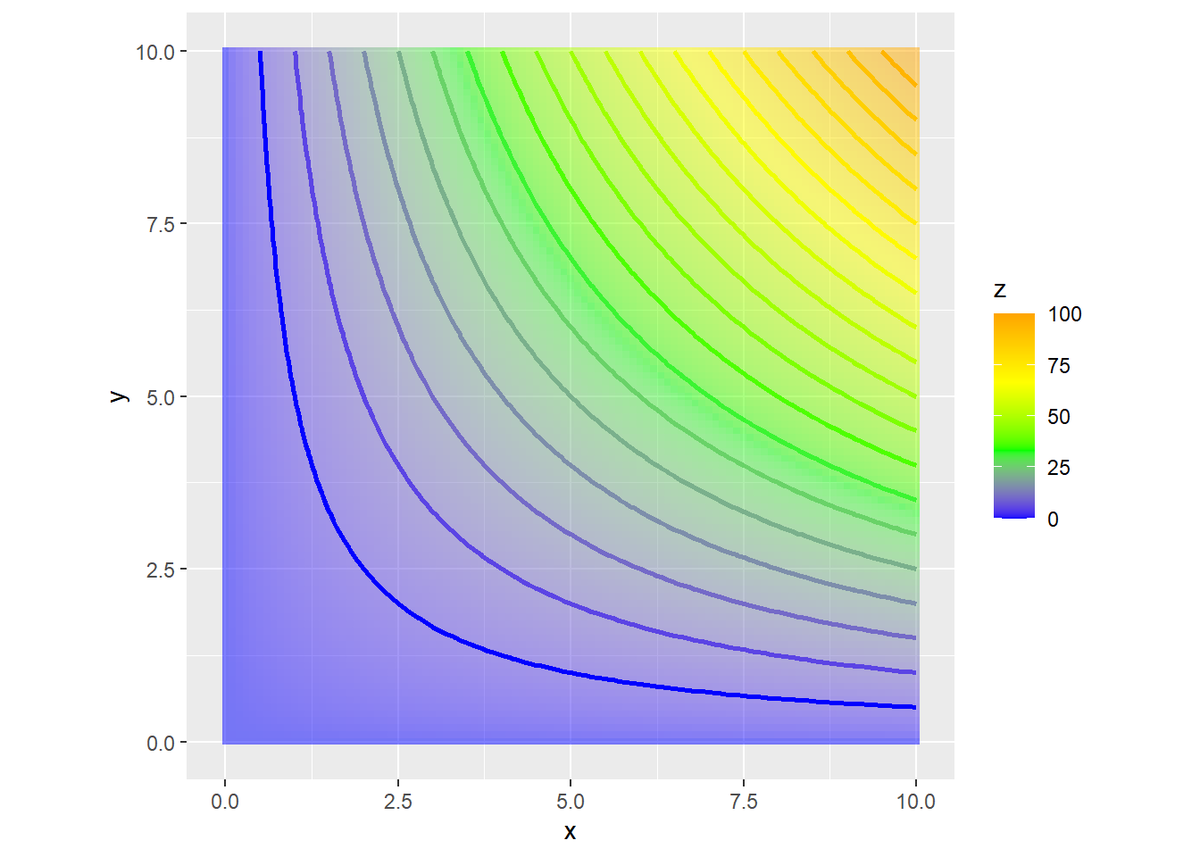
　一番左側の青色の曲線が$f(x, y) = 5$となる2辺の組み合わせを表す。

　ここに、制約曲線$g(x, y)$を加える(この例だと直線になる)。

# 制約のデータフレームを作成
g_xy <- tibble(
  x = seq(0, 10, 0.1), 
  y = 10 - x
)

# 面積と制約の関係を可視化
ggplot() + 
  geom_tile(data = f_xy, mapping = aes(x = x, y = y, fill = z), alpha = 0.5) + # ヒートマップ
  scale_fill_gradientn(colors = c("blue", "green", "yellow", "orange")) + # タイルの色
  geom_contour(data = f_xy, aes(x = x, y = y, z = z, color = stat(level)), 
               binwidth = 5, size = 1) + # 等高線
  scale_color_gradientn(colors = c("blue", "green", "yellow", "orange")) + # 線の色
  geom_line(data = g_xy, mapping = aes(x = x, y = y), size = 1) + # 折れ線グラフ
  guides(color = FALSE) + # 凡例
  coord_fixed(ratio = 1) # 縦横比

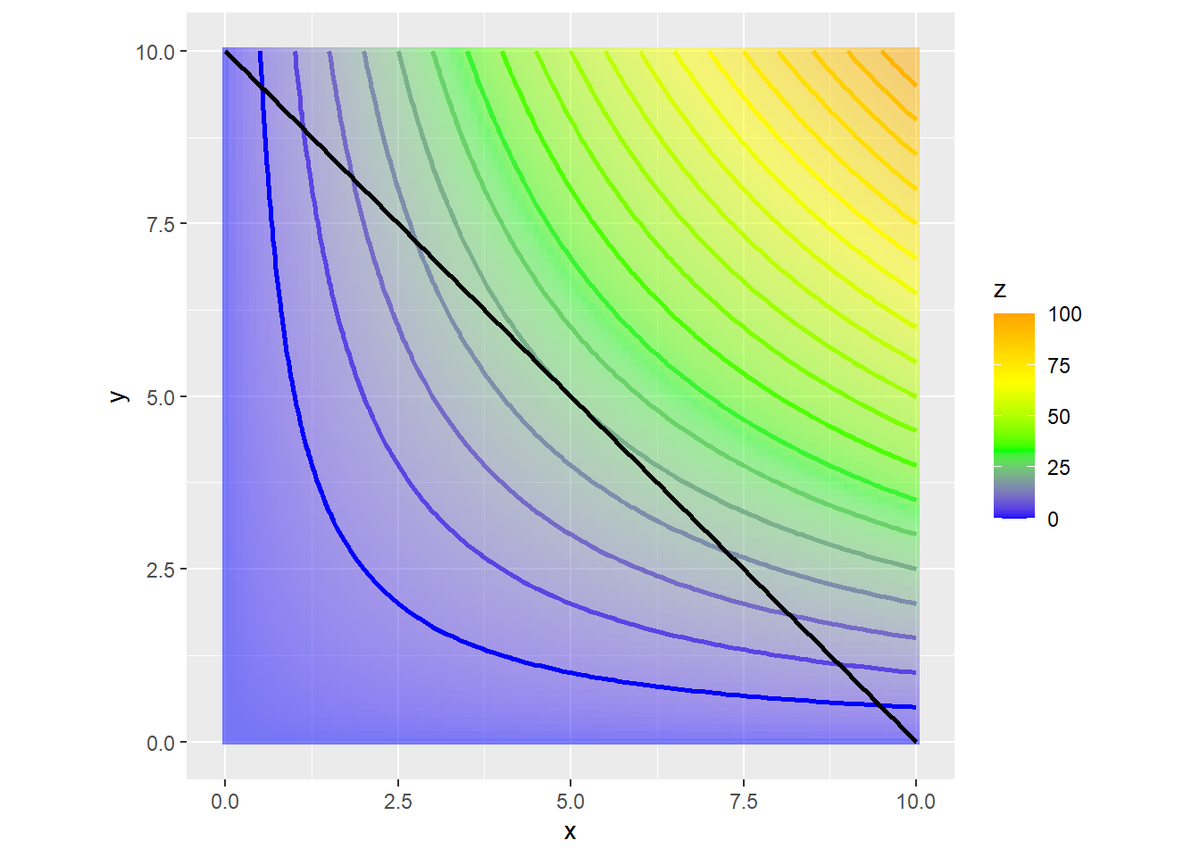
　制約曲線$g(x, y)$上の点が、制約$x + y = 10$を満たす2辺の組み合わせである。この中で面積$f(x, y)$を最大化する点は、$f(x, y) = 25$の曲線との接点$(x = 5, y = 5)$であることが分かる。

　本(トピックモデル)では、(変分)下限を最大化するパラメータ(分布)を求める際に、確率分布の定義(総和や積分すると1になる)に従う必要がある。そこでラグランジュの未定乗数法を用いて、制約付き最適化問題として解く。

参考書籍

岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社

おわりに

2019/08/23：加筆修正しました。

2020/06/11：加筆修正しました。

　その際に、記事の一部を1つ前の記事に移しました。

【次節の内容】

からっぽのしょこ

読んだら書く！書いたら読む！同じ事は二度調べ(たく)ない

1.1.11：ラグランジュの未定乗数法【『トピックモデル』の勉強ノート】

はじめに

1.1.11 ラグランジュの未定乗数法

・例題

参考書籍

おわりに