はじめに
『スタンフォード ベクトル・行列からはじめる最適化数学』の学習ノートです。
「数式の行間埋め」や「Pythonを使っての再現」によって理解を目指します。本と一緒に読んでください。
この記事は1.3節「ベクトルスカラー積」の内容です。
任意の係数によるベクトルの線形結合を可視化します。
【前の内容】
【他の内容】
【今回の内容】
ベクトルの線形結合の可視化
ベクトルの線形結合(linear combination)をグラフで確認します。
ベクトルの和については「【Python】ベクトルの和の例【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」、ベクトルの定数倍については「【Python】1.3:ベクトルのスカラー積の例【『スタンフォード線形代数入門』のノート】 - からっぽのしょこ」を参照してください。
利用するライブラリを読み込みます。
# 利用ライブラリ import numpy as np import matplotlib.pyplot as plt from matplotlib.animation import FuncAnimation
2次元の場合
まずは、2次元空間(平面)上でベクトルの線形結合を可視化します。
2次元ベクトルと係数(スカラー値)を指定します。
# ベクトルを指定 a1 = np.array([4.0, 0.0]) a2 = np.array([2.0, 2.0]) # 係数を指定 beta1 = 0.75 beta2 = 1.5
を
a1, a2、係数を
beta1, beta2として値を指定します。ただし、Pythonでは0からインデックスが割り当てられるので、の値は
a1[0]に対応します。
2次元空間上に2つのベクトルを描画します。
# 作図用の値を設定 x_min = np.floor(np.min([0.0, a1[0], a2[0]])) - 1 x_max = np.ceil(np.max([0.0, a1[0], a2[0]])) + 1 y_min = np.floor(np.min([0.0, a1[1], a2[1]])) - 1 y_max = np.ceil(np.max([0.0, a1[1], a2[1]])) + 1 # (原点からの)2Dベクトルを作図 fig, ax = plt.subplots(figsize=(6, 4.5), facecolor='white') ax.quiver(0, 0, *a1, color='red', angles='xy', scale_units='xy', scale=1) # ベクトルa1 ax.quiver(0, 0, *a2, color='blue', angles='xy', scale_units='xy', scale=1) # ベクトルa2 ax.annotate(xy=0.5*a1, text='$a_1$', size=15, ha='center', va='top') # ベクトルa1ラベル ax.annotate(xy=0.5*a2, text='$a_2$', size=15, ha='right', va='bottom') # ベクトルa2ラベル ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.grid() ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('$a_1=('+', '.join(map(str, a1))+'), ' + 'a_2=('+', '.join(map(str, a2))+')$', loc='left') fig.suptitle('$a_1, a_2$', fontsize=20) ax.set_aspect('equal') plt.show()
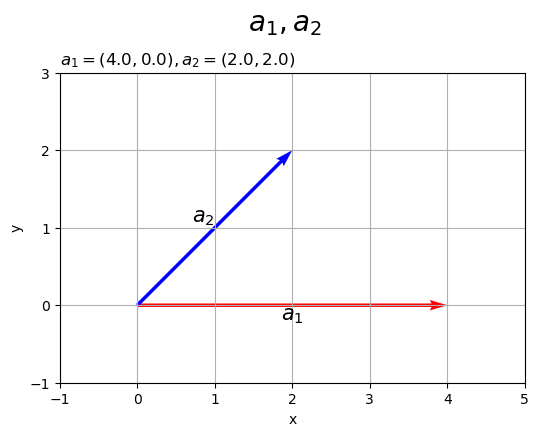
ベクトルのグラフを
axes.quiver()で描画します。第1・2引数に始点の座標、第3・4引数にベクトルのサイズ(変化量)を指定します。この例では、原点を始点とします。
配列a1, a2の前に*を付けてアンパック(展開)して指定しています。
のベクトルを描画します。
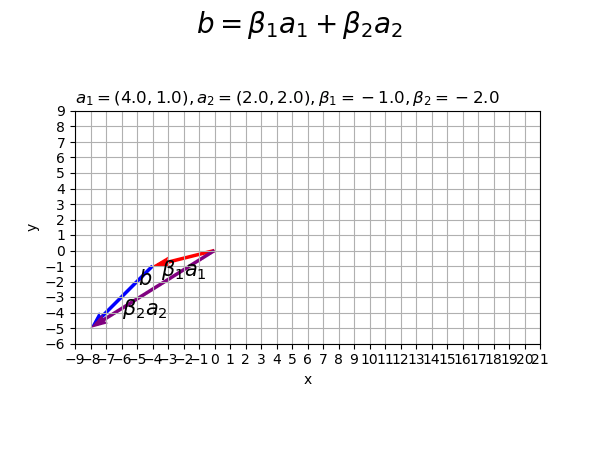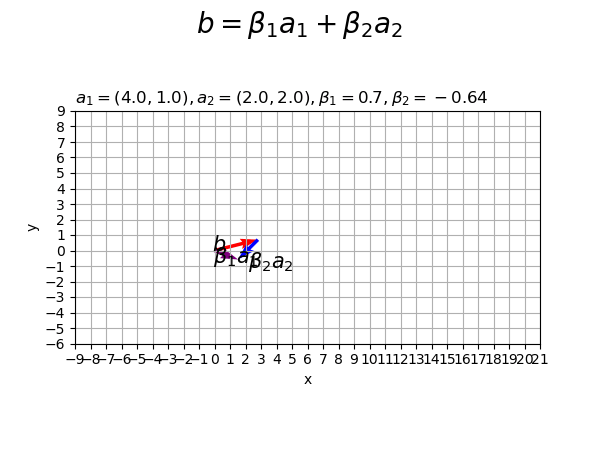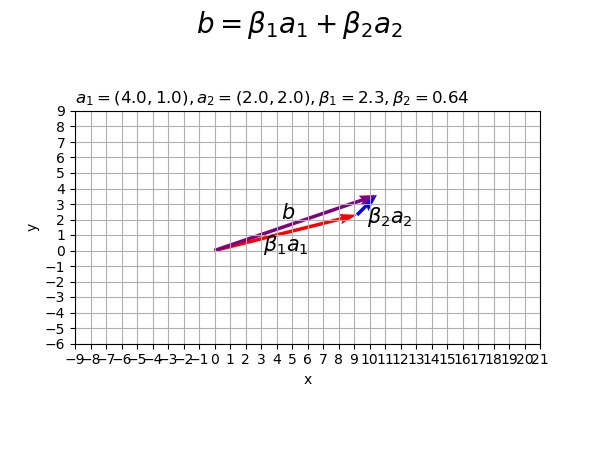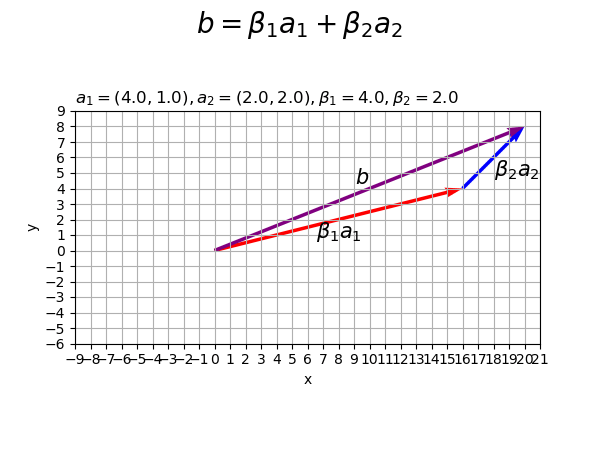
# 作図用の値を設定 x_min = np.floor(np.min([0.0, beta1*a1[0], beta1*a1[0]+beta2*a2[0]])) - 1 x_max = np.ceil(np.max([0.0, beta1*a1[0], beta1*a1[0]+beta2*a2[0]])) + 1 y_min = np.floor(np.min([0.0, beta1*a1[1], beta1*a1[1]+beta2*a2[1]])) - 1 y_max = np.ceil(np.max([0.0, beta1*a1[1], beta1*a1[1]+beta2*a2[1]])) + 1 # 2Dベクトルの線形結合を作図 fig, ax = plt.subplots(figsize=(6, 4.5), facecolor='white') ax.quiver(0, 0, *beta1*a1, color='red', angles='xy', scale_units='xy', scale=1) # ベクトルβ1a1 ax.quiver(*beta1*a1, *beta2*a2, color='blue', angles='xy', scale_units='xy', scale=1) # ベクトルβ2a2 ax.quiver(0, 0, *beta1*a1+beta2*a2, color='purple', angles='xy', scale_units='xy', scale=1) # ベクトルb ax.annotate(xy=0.5*beta1*a1, text='$\\beta_1 a_1$', size=15, ha='center', va='top') # ベクトルβ1a1ラベル ax.annotate(xy=beta1*a1+0.5*beta2*a2, text='$\\beta_2 a_2$', size=15, ha='left', va='top') # ベクトルβ2a2ラベル ax.annotate(xy=0.5*(beta1*a1+beta2*a2), text='$b$', size=15, ha='right', va='bottom') # ベクトルbラベル ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.grid() ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('$a_1=('+', '.join(map(str, a1))+'), ' + 'a_2=('+', '.join(map(str, a2))+'), ' + '\\beta_1='+str(beta1)+', ' + '\\beta_2='+str(beta2)+'$', loc='left') fig.suptitle('$b = \\beta_1 a_1 + \\beta_2 a_2$', fontsize=20) ax.set_aspect('equal') plt.show()
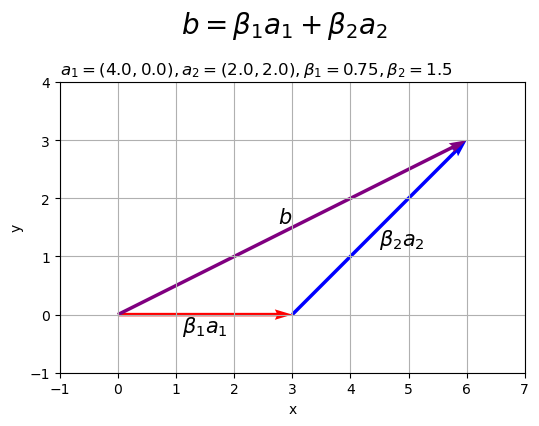
ベクトルとスカラーの積和(線形結合)を
とします。
係数の値を変化させたアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を設定 frame_num = 51 # ベクトルを指定 a1 = np.array([4.0, 1.0]) a2 = np.array([2.0, 2.0]) # 係数として利用する値を指定 beta1_vals = np.linspace(start=-1.0, stop=4.0, num=frame_num) beta2_vals = np.linspace(start=-2.0, stop=2.0, num=frame_num) # 作図用の値を設定 x_min = np.floor(np.min([0.0, *beta1_vals*a1[0], *beta1_vals*a1[0]+beta2_vals*a2[0]])) - 1 x_max = np.ceil(np.max([0.0, *beta1_vals*a1[0], *beta1_vals*a1[0]+beta2_vals*a2[0]])) + 1 y_min = np.floor(np.min([0.0, *beta1_vals*a1[1], *beta1_vals*a1[1]+beta2_vals*a2[1]])) - 1 y_max = np.ceil(np.max([0.0, *beta1_vals*a1[1], *beta1_vals*a1[1]+beta2_vals*a2[1]])) + 1 # 作図用のオブジェクトを初期化 fig, ax = plt.subplots(figsize=(6, 4.5), facecolor='white') fig.suptitle('$b = \\beta_1 a_1 + \\beta_2 a_2$', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の係数を作成 beta1 = beta1_vals[i] beta2 = beta2_vals[i] # 2Dベクトルの線形結合を作図 ax.quiver(0, 0, *beta1*a1, color='red', angles='xy', scale_units='xy', scale=1) # ベクトルa1 ax.quiver(*beta1*a1, *beta2*a2, color='blue', angles='xy', scale_units='xy', scale=1) # ベクトルa2 ax.quiver(0, 0, *beta1*a1+beta2*a2, color='purple', angles='xy', scale_units='xy', scale=1) # ベクトルb ax.annotate(xy=0.5*beta1*a1, text='$\\beta_1 a_1$', size=15, ha='center', va='top') # ベクトルa1ラベル ax.annotate(xy=beta1*a1+0.5*beta2*a2, text='$\\beta_2 a_2$', size=15, ha='left', va='top') # ベクトルa2ラベル ax.annotate(xy=0.5*(beta1*a1+beta2*a2), text='$b$', size=15, ha='right', va='bottom') # ベクトルbラベル ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.grid() ax.set_xlabel('x') ax.set_ylabel('y') ax.set_title('$a_1=('+', '.join(map(str, a1))+'), ' + 'a_2=('+', '.join(map(str, a2))+'), ' + '\\beta_1='+str(beta1.round(2))+', ' + '\\beta_2='+str(beta2.round(2))+'$', loc='left') ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('linearcomb_2d.gif')
作図処理をupdate()として定義して、FuncAnimation()でgif画像を作成します。
3次元の場合
続いて、3次元空間上での線形結合を可視化します。
3次元ベクトルと係数を指定します。
# ベクトルを指定 a1 = np.array([4.0, 0.0, -1.0]) a2 = np.array([2.0, 2.0, 2.0]) # 係数を指定 beta1 = 0.75 beta2 = 1.5
を
a1, a2、係数を
beta1, beta2として値を指定します。
3次元空間上に2つのベクトルを描画します。
# 作図用の値を設定 x_min = np.floor(np.min([0.0, a1[0], a2[0]])) - 1 x_max = np.ceil(np.max([0.0, a1[0], a2[0]])) + 1 y_min = np.floor(np.min([0.0, a1[1], a2[1]])) - 1 y_max = np.ceil(np.max([0.0, a1[1], a2[1]])) + 1 z_min = np.floor(np.min([0.0, a1[2], a2[2]])) - 1 z_max = np.ceil(np.max([0.0, a1[2], a2[2]])) + 1 # (原点からの)3Dベクトルを作図 fig, ax = plt.subplots(subplot_kw={'projection': '3d'}, figsize=(7, 7), facecolor='white') ax.quiver(0, 0, 0, *a1, arrow_length_ratio=0.05, color='red') # ベクトルa1 ax.quiver(0, 0, 0, *a2, arrow_length_ratio=0.05, color='blue') # ベクトルa2 ax.text(*0.5*a1, s='$a_1$', size=15, ha='center', va='top') # ベクトルa1ラベル ax.text(*0.5*a2, s='$a_2$', size=15, ha='right', va='bottom') # ベクトルa2ラベル ax.quiver([0, a1[0], a2[0]], [0, a1[1], a2[1]], [z_min, z_min, z_min], [0, 0, 0], [0, 0, 0], [-z_min, a1[2]-z_min, a2[2]-z_min], color='gray', arrow_length_ratio=0, linestyle=':') # 補助線 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$a_1=('+', '.join(map(str, a1))+'), ' + 'a_2=('+', '.join(map(str, a2))+')$', loc='left') fig.suptitle('$a_1, a_2$', fontsize=20) ax.set_aspect('equal') plt.show()
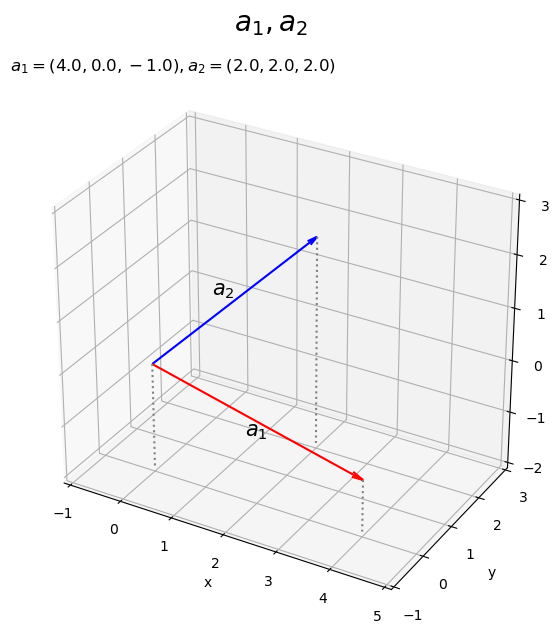
axes.quiver()の第1・2・3引数に始点の座標、第4・5・6引数にベクトルのサイズを指定します。この例では、原点を始点とします。
のベクトルを描画します。
# 作図用の値を設定 x_min = np.floor(np.min([0.0, beta1*a1[0], beta1*a1[0]+beta2*a2[0]])) - 1 x_max = np.ceil(np.max([0.0, beta1*a1[0], beta1*a1[0]+beta2*a2[0]])) + 1 y_min = np.floor(np.min([0.0, beta1*a1[1], beta1*a1[1]+beta2*a2[1]])) - 1 y_max = np.ceil(np.max([0.0, beta1*a1[1], beta1*a1[1]+beta2*a2[1]])) + 1 z_min = np.floor(np.min([0.0, beta1*a1[2], beta1*a1[2]+beta2*a2[2]])) - 1 z_max = np.ceil(np.max([0.0, beta1*a1[2], beta1*a1[2]+beta2*a2[2]])) + 1 # 3Dベクトルの線形結合を作図 fig, ax = plt.subplots(subplot_kw={'projection': '3d'}, figsize=(7, 7), facecolor='white') ax.quiver(0, 0, 0, *beta1*a1, arrow_length_ratio=0.05, color='red') # ベクトルβ1a1 ax.quiver(*beta1*a1, *beta2*a2, arrow_length_ratio=0.05, color='blue') # ベクトルβ2a2 ax.quiver(0, 0, 0, *beta1*a1+beta2*a2, arrow_length_ratio=0.05, color='purple') # ベクトルb ax.text(*0.5*beta1*a1, s='$\\beta_1 a_1$', size=15, ha='center', va='top') # ベクトルβ1a1ラベル ax.text(*beta1*a1+0.5*beta2*a2, s='$\\beta_2 a_2$', size=15, ha='left', va='top') # ベクトルβ2a2ラベル ax.text(*0.5*(beta1*a1+beta2*a2), s='$b$', size=15, ha='right', va='bottom') # ベクトルbラベル ax.quiver([0, beta1*a1[0], beta1*a1[0]+beta2*a2[0]], [0, beta1*a1[1], beta1*a1[1]+beta2*a2[1]], [z_min, z_min, z_min], [0, 0, 0], [0, 0, 0], [-z_min, beta1*a1[2]-z_min, beta1*a1[2]+beta2*a2[2]-z_min], color='gray', arrow_length_ratio=0, linestyle=':') # 補助線 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$a_1=('+', '.join(map(str, a1))+'), ' + 'a_2=('+', '.join(map(str, a2))+'), ' + '\\beta_1='+str(beta1)+', ' + '\\beta_2='+str(beta2)+'$', loc='left') fig.suptitle('$b = \\beta_1 a_1 + \\beta_2 a_2$', fontsize=20) ax.set_aspect('equal') plt.show()
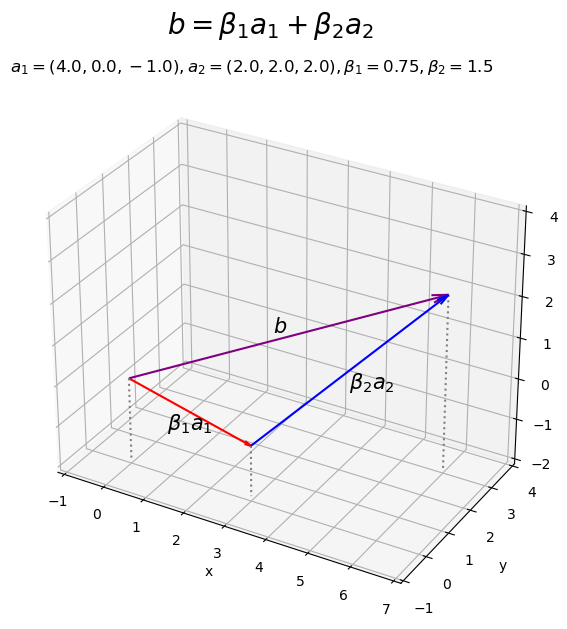
線形結合したベクトルをとします。
係数の値を変化させたアニメーションを作成します。
・作図コード(クリックで展開)
# フレーム数を設定 frame_num = 51 # ベクトルを指定 a1 = np.array([4.0, 0.0, -1.0]) a2 = np.array([2.0, 2.0, 2.0]) # 係数として利用する値を指定 beta1_vals = np.linspace(start=-1.5, stop=3.5, num=frame_num) beta2_vals = np.linspace(start=-3.0, stop=3.0, num=frame_num) # 作図用の値を設定 x_min = np.floor(np.min([0.0, *beta1_vals*a1[0], *beta1_vals*a1[0]+beta2_vals*a2[0]])) - 1 x_max = np.ceil(np.max([0.0, *beta1_vals*a1[0], *beta1_vals*a1[0]+beta2_vals*a2[0]])) + 1 y_min = np.floor(np.min([0.0, *beta1_vals*a1[1], *beta1_vals*a1[1]+beta2_vals*a2[1]])) - 1 y_max = np.ceil(np.max([0.0, *beta1_vals*a1[1], *beta1_vals*a1[1]+beta2_vals*a2[1]])) + 1 z_min = np.floor(np.min([0.0, *beta1_vals*a1[2], *beta1_vals*a1[2]+beta2_vals*a2[2]])) - 1 z_max = np.ceil(np.max([0.0, *beta1_vals*a1[2], *beta1_vals*a1[2]+beta2_vals*a2[2]])) + 1 # 作図用のオブジェクトを初期化 fig, ax = plt.subplots(subplot_kw={'projection': '3d'}, figsize=(7, 7), facecolor='white') fig.suptitle('$b = \\beta_1 a_1 + \\beta_2 a_2$', fontsize=20) # 作図処理を関数として定義 def update(i): # 前フレームのグラフを初期化 plt.cla() # i番目の係数を作成 beta1 = beta1_vals[i] beta2 = beta2_vals[i] # 3Dベクトルの線形結合を作図 ax.quiver(0, 0, 0, *beta1*a1, arrow_length_ratio=0.05, color='red') # ベクトルβ1a1 ax.quiver(*beta1*a1, *beta2*a2, arrow_length_ratio=0.05, color='blue') # ベクトルβ2a2 ax.quiver(0, 0, 0, *beta1*a1+beta2*a2, arrow_length_ratio=0.05, color='purple') # ベクトルb ax.text(*0.5*beta1*a1, s='$\\beta_1 a_1$', size=15, ha='center', va='top') # ベクトルβ1a1ラベル ax.text(*beta1*a1+0.5*beta2*a2, s='$\\beta_2 a_2$', size=15, ha='left', va='top') # ベクトルβ2a2ラベル ax.text(*0.5*(beta1*a1+beta2*a2), s='$b$', size=15, ha='right', va='bottom') # ベクトルbラベル ax.quiver([0, beta1*a1[0], beta1*a1[0]+beta2*a2[0]], [0, beta1*a1[1], beta1*a1[1]+beta2*a2[1]], [z_min, z_min, z_min], [0, 0, 0], [0, 0, 0], [-z_min, beta1*a1[2]-z_min, beta1*a1[2]+beta2*a2[2]-z_min], color='gray', arrow_length_ratio=0, linestyle=':') # 補助線 ax.set_xticks(ticks=np.arange(x_min, x_max+1)) ax.set_yticks(ticks=np.arange(y_min, y_max+1)) ax.set_zticks(ticks=np.arange(z_min, z_max+1)) ax.set_zlim(z_min, z_max) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') ax.set_title('$a_1=('+', '.join(map(str, a1))+'), ' + 'a_2=('+', '.join(map(str, a2))+'), ' + '\\beta_1='+str(beta1.round(2))+', ' + '\\beta_2='+str(beta2.round(2))+'$', loc='left') ax.set_aspect('equal') # gif画像を作成 ani = FuncAnimation(fig=fig, func=update, frames=frame_num, interval=100) # gif画像を保存 ani.save('linearcomb_3d.gif')
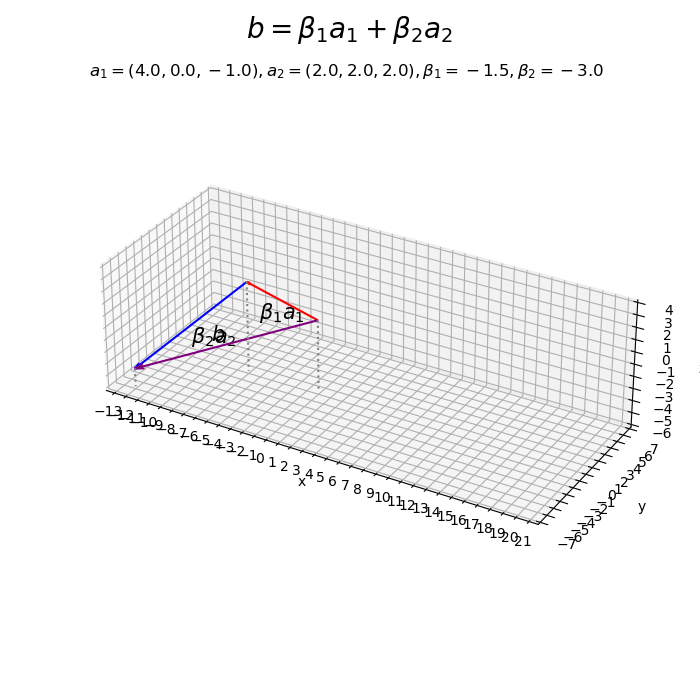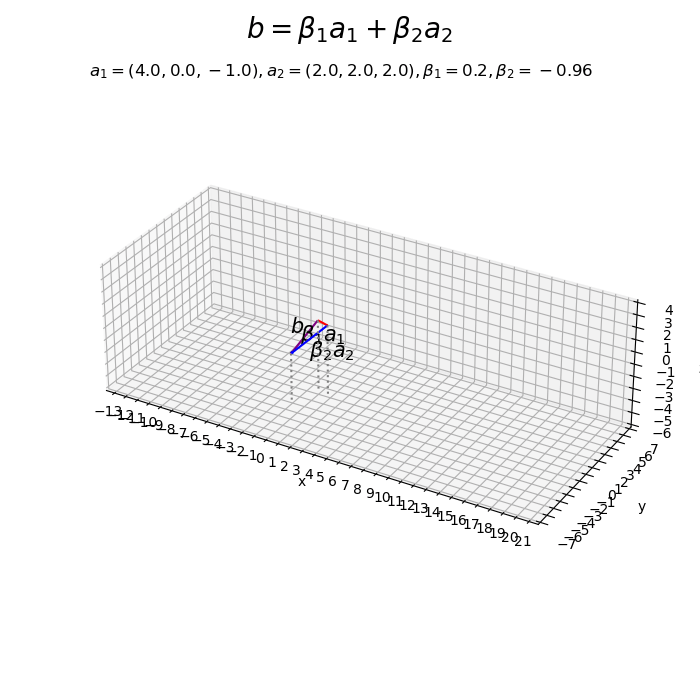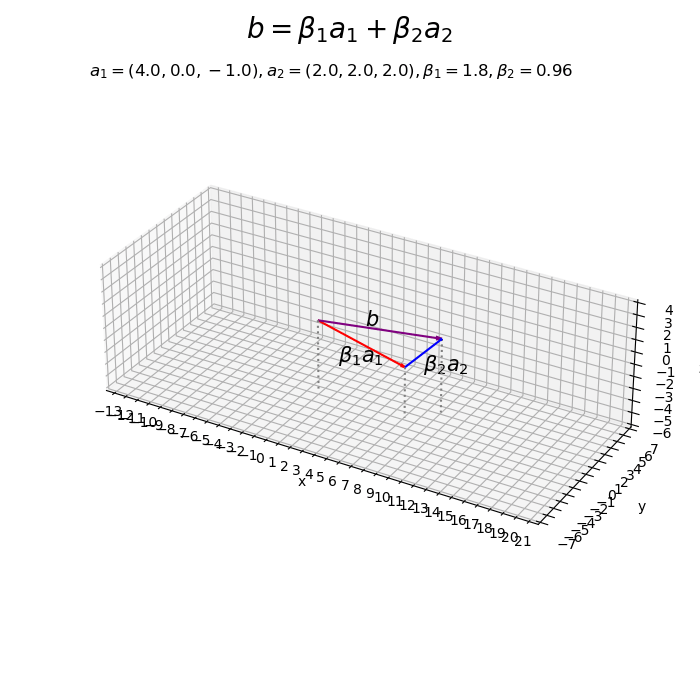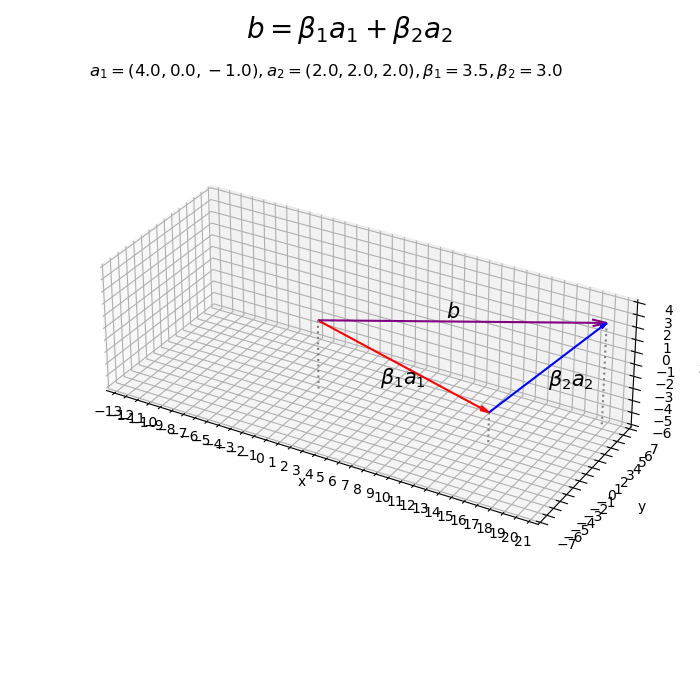
この記事では、任意の係数によるベクトルの線形結合を可視化しました。次の記事では、標準単位ベクトルの線形結合を可視化します。
参考書籍
- Stephen Boyd・Lieven Vandenberghe(著),玉木 徹(訳)『スタンフォード ベクトル・行列からはじめる最適化数学』講談社サイエンティク,2021年.
おわりに
スカラー積とベクトル和が組み合わさったのが線形結合ですね。伏線回収的に話が回り出すと面白さが上がってきますよね。
【次の内容】