はじめに
機械学習で登場する確率分布について色々な角度から理解したいシリーズです。
この記事では、R言語でウィシャート分布の乱数を生成します。ただし、グラフ化については試作です。
【前の内容】
【他の記事一覧】
【この記事の内容】
ウィシャート分布の乱数生成
ウィシャート分布(Wishart Distribution)の乱数を生成します。ウィシャート分布については「ウィシャート分布の定義式 - からっぽのしょこ」を参照してください。
利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はありません。ただし、作図コードがごちゃごちゃしないようにパッケージ名を省略しているため、ggplot2は読み込む必要があります。
magrittrパッケージのパイプ演算子%>%ではなく、ベースパイプ(ネイティブパイプ)演算子|>を使っています。%>%に置き換えても処理できます。
分布の変化をアニメーション(gif画像)で確認するのにgganimateパッケージを利用します。不要であれば省略してください。
サンプリング
まずは、ウィシャート分布の乱数を生成します。
ウィシャート分布のパラメータ$\nu, \mathbf{W}$とデータ数$N$を設定します。
# 次元数を指定 D <- 4 # 自由度を指定 nu <- D + 2 # 逆スケール行列を指定 w_dd <- c( 6, 0, 1, 4, 0, 2.4, -1, 0, 1, -1, 3.6, -1.7, 4, 0, -1.7, 4.8 ) |> # 値を指定 matrix(nrow = D, ncol = D) # マトリクスに変換 # 逆スケール行列をランダムに設定 #w_dd <- rWishart(n = 1, df = D, Sigma = diag(D))[, , 1] # データ数(サンプルサイズ)を指定 N <- 5000
次元数$D$と自由度$\nu$、逆スケール行列$\mathbf{W}$、またデータ数(サンプルサイズ)$N$を指定します。
自由度は$\nu > D - 1$、逆スケール行列は$D \times D$の正定値行列を満たす必要があります。設定した値に従う確率密度を計算します。
ウィシャート分布に従う乱数を生成します。
# ウィシャート分布に従う乱数を生成 lambda_ddn <- rWishart(n = N, df = nu, Sigma = w_dd) lambda_ddn[, , 1:3]
## , , 1 ## ## [,1] [,2] [,3] [,4] ## [1,] 46.141658 1.765864 12.680217 25.646221 ## [2,] 1.765864 6.434935 -3.131931 1.759187 ## [3,] 12.680217 -3.131931 15.142235 -1.192385 ## [4,] 25.646221 1.759187 -1.192385 21.497283 ## ## , , 2 ## ## [,1] [,2] [,3] [,4] ## [1,] 39.949803 8.9792027 5.2688935 25.197446 ## [2,] 8.979203 11.5618130 -0.5882512 3.401382 ## [3,] 5.268894 -0.5882512 9.2844535 -3.278399 ## [4,] 25.197446 3.4013822 -3.2783990 23.343710 ## ## , , 3 ## ## [,1] [,2] [,3] [,4] ## [1,] 43.126648 -8.058262 6.216177 29.238000 ## [2,] -8.058262 20.367665 -0.686613 -11.680628 ## [3,] 6.216177 -0.686613 13.407265 -2.287181 ## [4,] 29.238000 -11.680628 -2.287181 25.910024
ウィシャート分布の乱数は、rWishart()で生成できます。データ数の引数nにN、自由度の引数dfにnu、逆スケール行列の引数Sigmaにw_ddを指定します。
生成した値をサンプル$\boldsymbol{\Lambda}_n = (\lambda_{1,1,n}, \cdots, \lambda_{D,D, n})$とします。
N個のサンプルをデータフレームに格納します。
# サンプルを格納 data_df <- tidyr::expand_grid( n = 1:N, # データ番号 i = 1:D, # 行インデックス j = 1:D # 列インデックス ) |> # サンプルごとに成分番号を複製 #dplyr::filter(i <= j) |> # 重複を削除 dplyr::group_by(n, i, j) |> # 値の抽出用にグループ化 dplyr::mutate( lambda = lambda_ddn[i, j, n] ) |> # 次元ごとに値を抽出 dplyr::ungroup() # グループ化を解除 data_df
## # A tibble: 80,000 × 4 ## n i j lambda ## <int> <int> <int> <dbl> ## 1 1 1 1 46.1 ## 2 1 1 2 1.77 ## 3 1 1 3 12.7 ## 4 1 1 4 25.6 ## 5 1 2 1 1.77 ## 6 1 2 2 6.43 ## 7 1 2 3 -3.13 ## 8 1 2 4 1.76 ## 9 1 3 1 12.7 ## 10 1 3 2 -3.13 ## # … with 79,990 more rows
データ番号(1からNの整数)と行番号と列番号(それぞれ1からDの整数)の全ての組み合わせをexpand_grid()で作成します。これにより、サンプルごとに全ての要素のインデックス(成分番号)を複製できます。
作成したインデックスを使って、lambda_ddnから各要素(成分)の値を抽出します。
乱数の可視化
続いて、生成した乱数のグラフを作成します。
ウィシャート分布の確率変数$\boldsymbol{\Lambda}$の各成分$\lambda_{i,j}$の期待値と最頻値を計算します。
# 統計量を計算 stat_df <- tidyr::expand_grid( i = 1:D, # 行インデックス j = 1:D # 列インデックス ) |> # 成分番号を作成 #dplyr::filter(i <= j) |> # 重複を削除 dplyr::group_by(i, j) |> # 値の抽出用にグループ化 dplyr::mutate( mean = nu * w_dd[i, j], # 期待値 mode = dplyr::if_else( condition = nu > D + 1, true = (nu - D - 1) * w_dd[i, j], false = as.numeric(NA) ) # 最頻値 ) |> # 次元ごとに統計量を計算 dplyr::ungroup() |> # グループ化を解除 tidyr::pivot_longer( cols = c(mean, mode), names_to = "type", values_to = "statistic" ) stat_df
## # A tibble: 32 × 4 ## i j type statistic ## <int> <int> <chr> <dbl> ## 1 1 1 mean 36 ## 2 1 1 mode 6 ## 3 1 2 mean 0 ## 4 1 2 mode 0 ## 5 1 3 mean 6 ## 6 1 3 mode 1 ## 7 1 4 mean 24 ## 8 1 4 mode 4 ## 9 2 1 mean 0 ## 10 2 1 mode 0 ## # … with 22 more rows
要素番号(行番号と列番号の全ての組み合わせ)を作成して、要素ごとに期待値$\mathbb{E}[\lambda_{i,j}] = \nu w_{i,j}$と最頻値$\mathrm{mode}[\lambda_{i,j}] = (\nu - D - 1) w_{i,j}$を計算します。ただし、最頻値は$\nu > D + 1$の場合に定義されます。
期待値の列と最頻値の列をpivot_longer()でまとめます。
逆スケール行列の各成分$w_{i,j}$の値を表示するためのデータフレームを作成します。
# 逆スケール行列ラベルを作成 label_df <- tidyr::expand_grid( i = 1:D, # 行インデックス j = 1:D # 列インデックス ) |> # 成分番号を作成 #dplyr::filter(i <= j) |> # 重複を削除 dplyr::group_by(i, j) |> # 値の抽出用にグループ化 dplyr::mutate( label = paste0("w[", i, j, "]==", round(w_dd[i, j], 2)) ) |> # 次元ごとにラベルを作成 dplyr::ungroup() # グループ化を解除 label_df
## # A tibble: 16 × 3 ## i j label ## <int> <int> <chr> ## 1 1 1 w[11]==6 ## 2 1 2 w[12]==0 ## 3 1 3 w[13]==1 ## (省略) ## 15 4 3 w[43]==-1.7 ## 16 4 4 w[44]==4.8
要素番号(成分番号)を作成して、w_ddの各要素の値を抽出し、expression()の記法の文字列を作成します。
パラメータの値を数式で表示するための文字列を作成します。
# 凡例用の設定を作成:(数式表示用) color_vec <- c(mean = "blue", mode = "chocolate") label_vec <- c(mean = expression(E(lambda[ij])), mode = expression(mode(lambda[ij])))
ギリシャ文字などの記号を使った数式を表示する場合は、expression()の記法を使います。等号は"=="、複数の(数式上の)変数を並べるには"list(変数1, 変数2)"とします。(プログラム上の)変数の値を使う場合は、parse()のtext引数に指定します。
サンプルの成分ごとのヒストグラムを作成します。
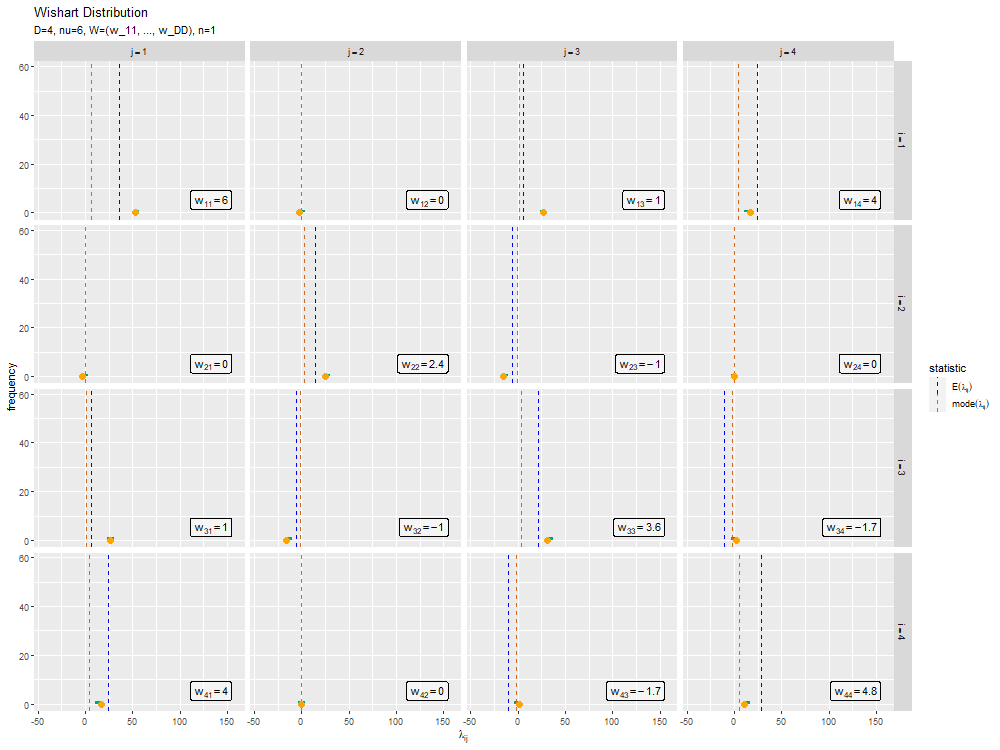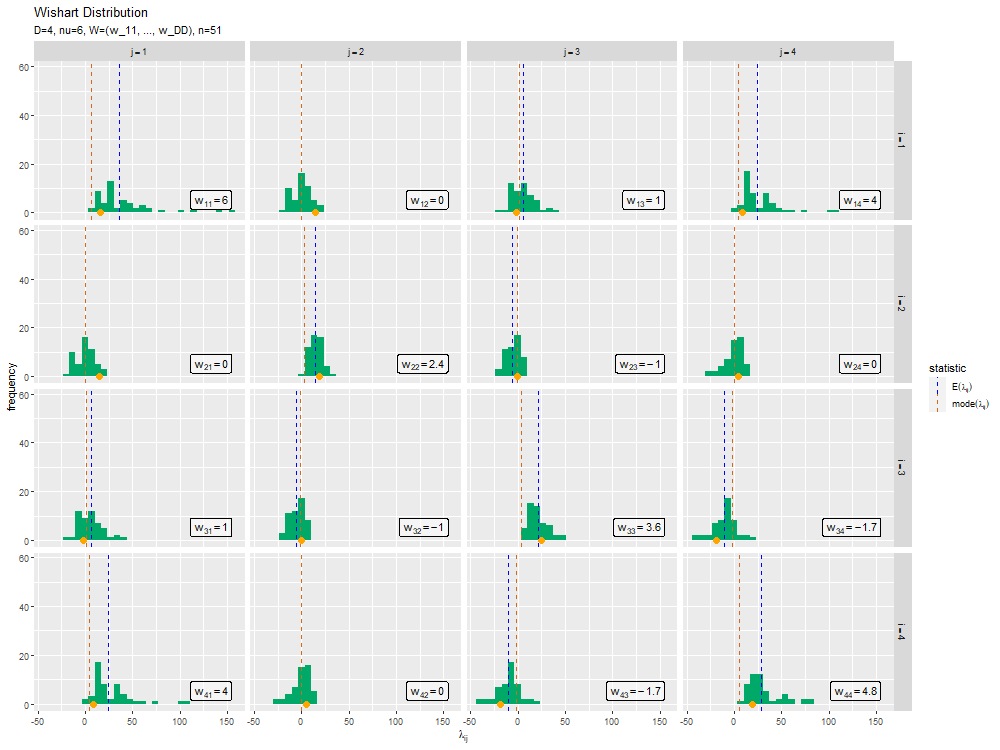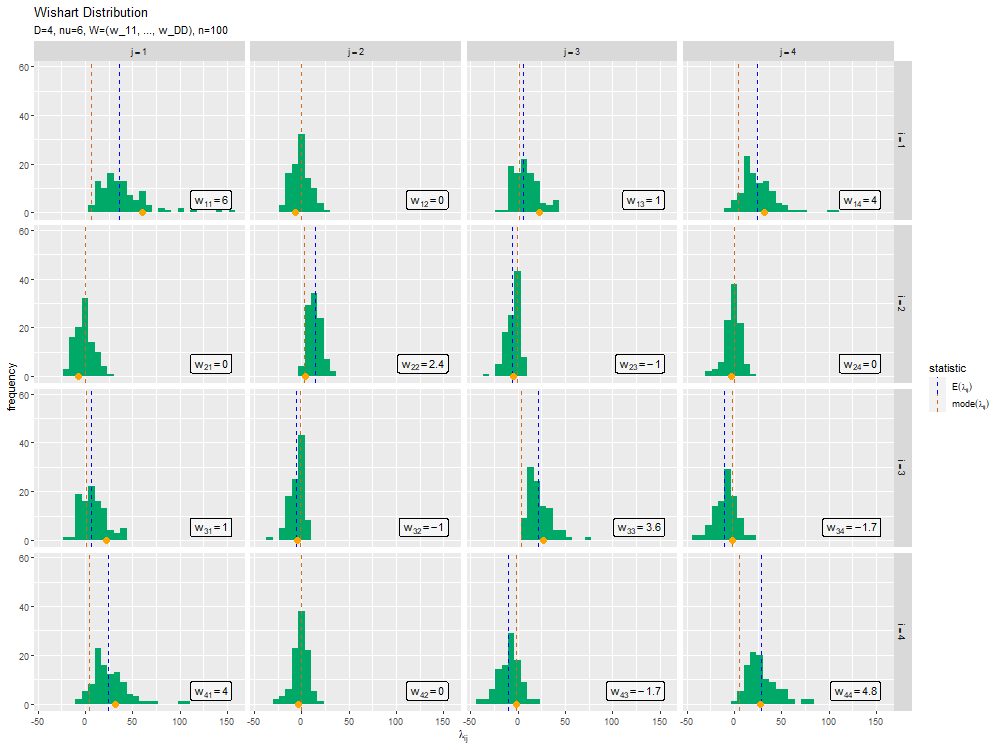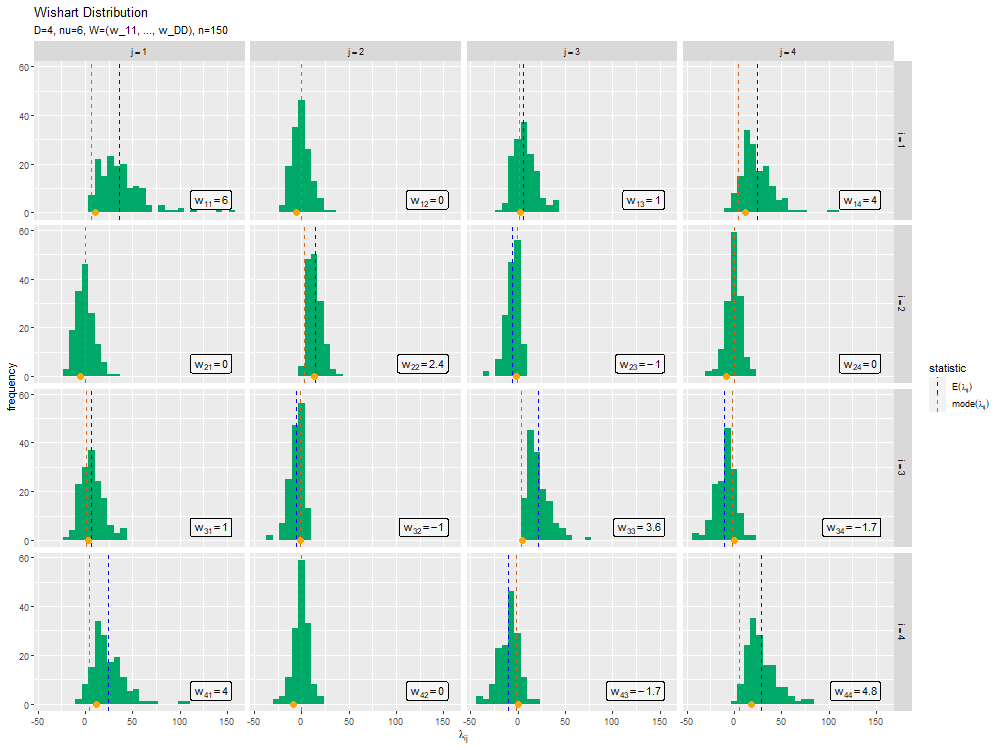
# サンプルのヒストグラムを作成 ggplot() + geom_histogram(data = data_df, mapping = aes(x = lambda, y = ..count..), bins = 50, fill = "#00A968") + # サンプル geom_vline(data = stat_df, mapping = aes(xintercept = statistic, color = type), linetype = "dashed") + # 統計量 geom_label(data = label_df, mapping = aes(x = max(lambda_ddn), y = N*0.01, label = label), parse = TRUE, hjust = "inward", vjust = "inward", alpha = 0.5) + # パラメータラベル facet_grid(i ~ j, labeller = label_bquote(rows = i==.(i), cols = j==.(j))) + # グラフの分割 scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(数式表示用) theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Wishart Distribution", subtitle = parse(text = paste0("list(D==", D, ", nu==", nu, ", W==(list(w[11], ..., w[DD])), N==", N, ")")), x = expression(lambda[ij]), y = "frequency")
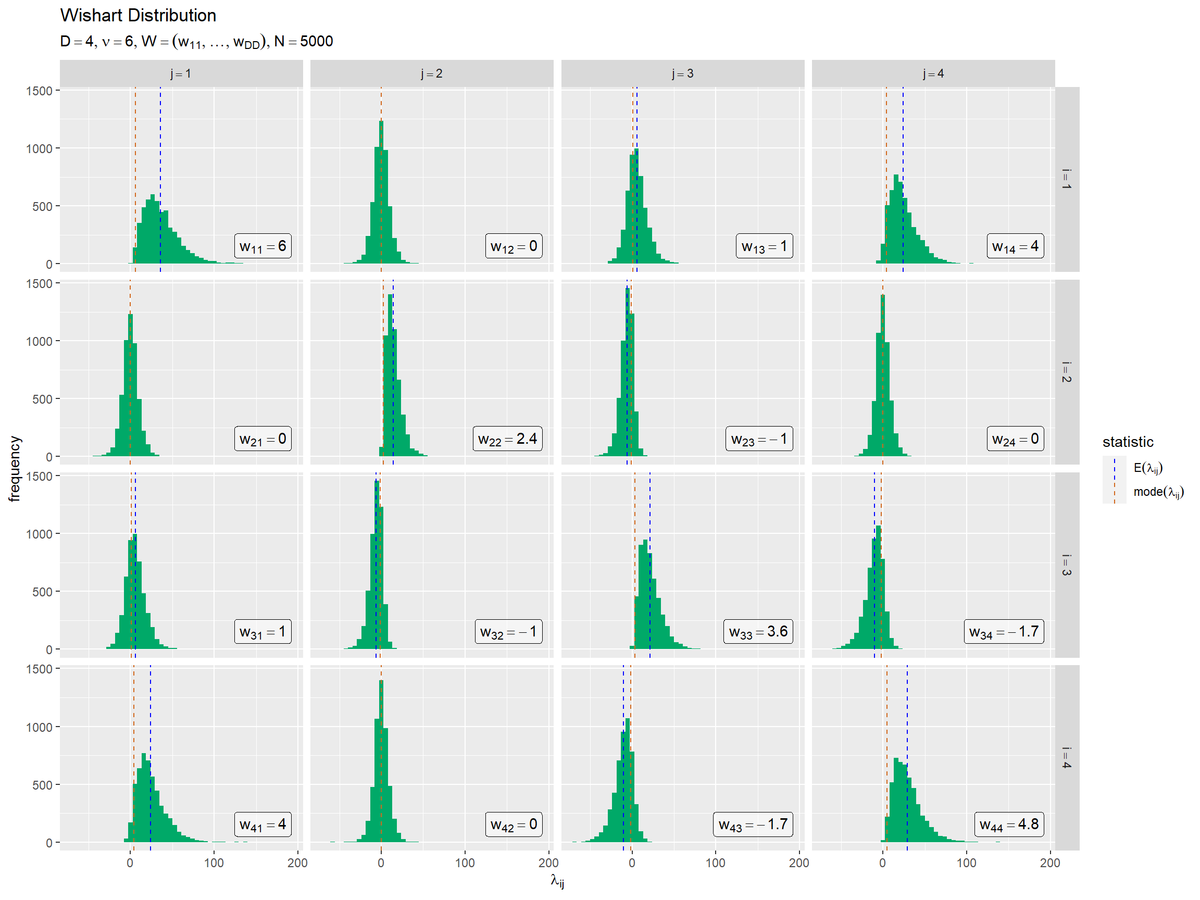
ヒストグラムはgeom_histgram()でを描画できます。デフォルト(y = ..count..)では、度数のヒストグラムを作成します。集計の範囲については、バーの数の引数binsまたはバーのサイズの引数binwidthを指定します。
facet_grid()に列1 ~ 列2を指定すると、列1の値に応じて縦方向に、列2の値に応じて横方向にグラフを分割して描画します。
($w_{i,j}$が0以外だと最頻値とヒストグラムにズレがあるのですが理由が分かりません。それと、各成分のヒストグラムの形が特徴的ですが、何かの分布だったりするのでしょうか。ガンマ分布っぽい気もしますが、負の値もあるのでそのものではないですね。)
乱数と分布の関係をアニメーションで可視化
次は、サンプルサイズとヒストグラムの形状の関係をアニメーションで確認します。
・作図コード(クリックで展開)
データ数を指定して、サンプルを生成します。
# データ数(フレーム数)を指定 N <- 250 # ウィシャート分布に従う乱数を生成 lambda_ddn <- rWishart(n = N, df = nu, Sigma = w_dd) lambda_ddn[, , 1:3]
## , , 1 ## ## [,1] [,2] [,3] [,4] ## [1,] 52.642332 -2.944715 26.707765 16.717801 ## [2,] -2.944715 25.194941 -15.769866 -0.314801 ## [3,] 26.707765 -15.769866 31.157433 1.934688 ## [4,] 16.717801 -0.314801 1.934688 11.120445 ## ## , , 2 ## ## [,1] [,2] [,3] [,4] ## [1,] 45.484783 4.676411 4.361609 34.416384 ## [2,] 4.676411 22.728539 -16.809952 8.537836 ## [3,] 4.361609 -16.809952 25.625261 -9.667811 ## [4,] 34.416384 8.537836 -9.667811 35.366842 ## ## , , 3 ## ## [,1] [,2] [,3] [,4] ## [1,] 17.939729 1.644608 -6.975887 19.007934 ## [2,] 1.644608 11.954917 -7.517959 5.369903 ## [3,] -6.975887 -7.517959 12.858186 -15.430808 ## [4,] 19.007934 5.369903 -15.430808 28.082545
lambda_ddnのn番目のマトリクスを、n番目のデータ(n回目にサンプリングされた値)とみなします。アニメーションのn番目のフレームでは、n個のサンプルlambda_ddn[, , 1:n]のグラフを描画します。
サンプルをデータフレームに格納します。
# サンプルを格納 anime_data_df <- tidyr::expand_grid( n = 1:N, # データ番号 i = 1:D, # 行インデックス j = 1:D # 列インデックス ) |> # サンプルごとに成分番号を複製 dplyr::group_by(n, i, j) |> # 値の抽出用にグループ化 dplyr::mutate( frame = n, # フレーム番号 lambda = lambda_ddn[i, j, n], # サンプルの値 parameter = paste0("D=", D, ", nu=", nu, ", W=(w_11, ..., w_DD)", ", n=", n) |> factor(levels = paste0("D=", D, ", nu=", nu, ", W=(w_11, ..., w_DD)", ", n=", 1:N)) # フレーム切替用ラベル ) |> # 次元ごとに値を抽出 dplyr::ungroup() # グループ化を解除 anime_data_df
## # A tibble: 2,400 × 6 ## n i j frame lambda parameter ## <int> <int> <int> <int> <dbl> <fct> ## 1 1 1 1 1 52.6 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 2 1 1 2 1 -2.94 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 3 1 1 3 1 26.7 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 4 1 1 4 1 16.7 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 5 1 2 1 1 -2.94 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 6 1 2 2 1 25.2 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 7 1 2 3 1 -15.8 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 8 1 2 4 1 -0.315 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 9 1 3 1 1 26.7 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 10 1 3 2 1 -15.8 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## # … with 2,390 more rows
サンプルlambda_ddnの各要素をデータフレームに格納して、フレーム切替用のラベルを作成します。ラベルが文字列型だと文字列の基準で順序が決まるので、因子型にしてサンプリング回数に応じたレベル(順序)を設定します。
このデータフレームは、各試行におけるサンプルを描画するのに使います。
サンプリング回数ごとに、それまでのサンプルを持つデータフレームを作成します。
# サンプルを複製して格納 anime_freq_df <- tidyr::expand_grid( frame = 1:N, # フレーム番号 n = 1:N, # データ番号 i = 1:D, # 行インデックス j = 1:D # 列インデックス ) |> # フレームとサンプルごとに成分番号を複製 dplyr::filter(n <= frame) |> # 各試行までのサンプルを抽出 dplyr::group_by(frame, n, i, j) |> # 値の抽出用にグループ化 dplyr::mutate( lambda = lambda_ddn[i, j, n], # サンプルの値 parameter = paste0("D=", D, ", nu=", nu, ", W=(w_11, ..., w_DD)", ", n=", frame) |> factor(levels = paste0("D=", D, ", nu=", nu, ", W=(w_11, ..., w_DD)", ", n=", 1:N)) # フレーム切替用ラベル ) |> # 次元ごとに値を抽出 dplyr::ungroup() # グループ化を解除 anime_freq_df
## # A tibble: 181,200 × 6 ## frame n i j lambda parameter ## <int> <int> <int> <int> <dbl> <fct> ## 1 1 1 1 1 52.6 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 2 1 1 1 2 -2.94 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 3 1 1 1 3 26.7 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 4 1 1 1 4 16.7 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 5 1 1 2 1 -2.94 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 6 1 1 2 2 25.2 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 7 1 1 2 3 -15.8 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 8 1 1 2 4 -0.315 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 9 1 1 3 1 26.7 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## 10 1 1 3 2 -15.8 D=4, nu=6, W=(w_11, ..., w_DD), n=1 ## # … with 181,190 more rows
フレーム番号とデータ番号(それぞれ1からNの整数)また行番号と列番号(それぞれ1からDの整数)の全ての組み合わせをexpand_grid()で作成して、フレーム番号以下のデータ番号を抽出します。
データ番号と成分番号をインデックスとして使って、lambda_ddnから対応するサンプルの要素を抽出します。
フレーム番号をデータ番号として、フレーム切替用のラベルを作成します。
このデータフレームは、ヒストグラムを描画するのに使います。
サンプルの散布図のアニメーション(gif画像)を作成します。
# ヒストグラムのアニメーションを作図 anime_freq_graph <- ggplot() + geom_label(data = label_df, mapping = aes(x = max(lambda_ddn), y = N*0.01, label = label), parse = TRUE, hjust = "inward", vjust = "inward", alpha = 0.5) + # 逆スケール行列ラベル geom_histogram(data = anime_freq_df, mapping = aes(x = lambda, y = ..count..), bins = 30, fill = "#00A968") + # n個のサンプル geom_vline(data = stat_df, mapping = aes(xintercept = statistic, color = type), linetype = "dashed") + # 統計量 geom_point(data = anime_data_df, mapping = aes(x = lambda, y = 0), color = "orange", size = 3) + # n番目のサンプル gganimate::transition_manual(parameter) + # フレーム facet_grid(i ~ j, labeller = label_bquote(rows = i==.(i), cols = j==.(j))) + # グラフの分割 scale_color_manual(values = color_vec, labels = label_vec, name = "statistic") + # 線の色:(数式表示用) theme(legend.text.align = 0) + # 図の体裁:凡例 labs(title = "Wishart Distribution", subtitle = "{current_frame}", x = expression(lambda[ij]), y = "frequency") # gif画像を作成 gganimate::animate(anime_freq_graph, nframes = N+10, end_pause = 10, fps = 10, width = 1000, height = 750)
transition_manual()にフレームの順序を表す列を指定します。この例では、因子型のラベルのレベルの順に描画されます。
animate()のフレーム数の引数nframesにデータ数(サンプルサイズ)、フレームレートの引数fpsに1秒当たりのフレーム数を指定します。fps引数の値が大きいほどフレームが早く切り替わります。ただし、値が大きいと指定した通りに動作しません。
この記事では、ウィシャート分布の乱数を生成しました。次は、多次元ガウス分布を生成しました。
参考文献
- C.M.ビショップ著,元田 浩・他訳『パターン認識と機械学習 上』,丸善出版,2012年.
おわりに
ウィシャート分布のグラフ化は難しいということで、乱数のヒストグラムならできるのではと思いやってみました。が、理論上の統計量とヒストグラムがズレるので、色々あるのでしょう。深い入りするのは今は止めときます。
【次の内容】