はじめに
『ベイズ推論による機械学習入門』の学習時のノートです。基本的な内容は「数式の行間を読んでみた」とそれを「RとPythonで組んでみた」になります。「数式」と「プログラム」から理解するのが目標です。
この記事は、3.3.3項の内容です。「尤度関数を平均と精度が未知の1次元ガウス分布(正規分布)」、「事前分布をガウス・ガンマ分布」とした場合の「パラメータの事後分布」と「未観測値の予測分布」の計算をPythonで実装します。
省略してある内容等ありますので、本とあわせて読んでください。初学者な自分が理解できるレベルまで落として書き下していますので、分かる人にはかなりくどくなっています。同じような立場の人のお役に立てれば幸いです。
【数式読解編】
【他の節の内容】
【この節の内容】
・Pythonでやってみよう
人工的に生成したデータを用いて、ベイズ推論を行ってみましょう。
利用するライブラリを読み込みます。
# 3.3.3項で利用するライブラリ import numpy as np import math # 対数ガンマ関数:lgamma() from scipy.stats import norm, gamma, t # 1次元ガウス分布, ガンマ分布, 1次元スチューデントのt分布 import matplotlib.pyplot as plt
この例では、ガンマ分布・1次元スチューデントのt分布の確率密度を求めるのにガンマ関数$\Gamma(\cdot)$の計算を行います。ガンマ関数の計算には、mathライブラリの対数をとったガンマ関数lgamma()を使います。
または、SciPyライブラリのnorm.pdf()・gamma.pdf()・t.pdf()で1次元ガウス分布・ガンマ分布・1次元スチューデントのt分布の確率密度を直接計算することもできます。
・モデルの構築
まずは、モデルを設定します。
尤度(ガウス分布)のパラメータを設定します。
# 真のパラメータを指定 mu_truth = 25 lambda_truth = 0.01
平均パラメータ$\mu$をmu_truth、精度パラメータ$\lambda$をlambda_truthとして値を指定します。精度は分散の逆数なので、値が大きいほど散らばり具合が小さくなり、逆数の平方根が標準偏差$\sigma = \sqrt{\lambda^{-1}}$になります。この2つが真のパラメータであり、この値を求めるのがここでの目的です。
尤度の確率密度を計算します。
# 作図用のxの値を設定 x_line = np.linspace( mu_truth - 4 * np.sqrt(1 / lambda_truth), mu_truth + 4 * np.sqrt(1 / lambda_truth), num=1000 ) # 尤度を計算:式(2.64) ln_C_N = - 0.5 *(np.log(2 * np.pi) - np.log(lambda_truth)) # 正規化項(対数) true_model = np.exp(ln_C_N - 0.5 * lambda_truth * (x_line - mu_truth)**2) # 確率密度 # 尤度を計算:SciPy ver #true_model = norm.pdf(x=x_line, loc=mu_truth, scale=np.sqrt(1 / lambda_truth)) # 確率密度
作図用に、ガウス分布に従う変数$x_n$がとり得る値をnp.linspace()で作成してx_lineとします。この例では、平均値を中心に標準偏差の4倍を範囲とします。np.linspace()を使うと指定した要素数で等間隔に切り分けます。np.arange()を使うと切り分ける間隔を指定できます。処理が重い場合は、この値を調整してください。
x_lineの値ごとに確率密度を計算します。1次元ガウス分布の確率密度は、対数をとった定義式
で計算して、最後にnp.exp()をします。scipy.statsのガウス分布の確率密度関数norm.pdf()でも計算できます。
計算結果を確認しましょう。
# 確認 print(x_line[:10]) print(true_model[:10])
[-15. -14.91991992 -14.83983984 -14.75975976 -14.67967968
-14.5995996 -14.51951952 -14.43943944 -14.35935936 -14.27927928]
[1.33830226e-05 1.38182046e-05 1.42666228e-05 1.47286482e-05
1.52046611e-05 1.56950518e-05 1.62002199e-05 1.67205753e-05
1.72565380e-05 1.78085384e-05]
これを使って作図します。
尤度を作図します。
# 尤度を作図 plt.figure(figsize=(12, 9)) plt.plot(x_line, true_model, color='purple') # 尤度 plt.xlabel('x') plt.ylabel('density') plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('$\mu=' + str(mu_truth) + ', \lambda=' + str(lambda_truth) + '$', loc='left') plt.show()
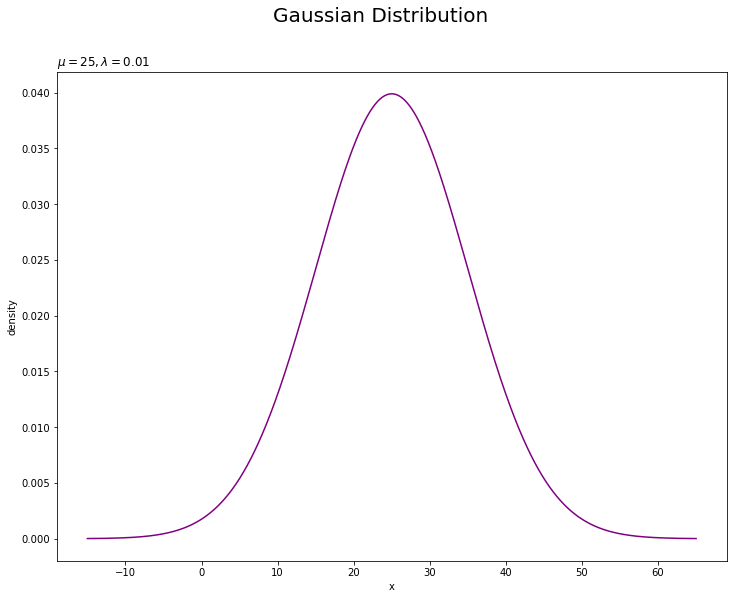
真のパラメータを求めることは、この真の分布を求めることを意味します。
・データの生成
続いて、構築したモデルに従って観測データ$\mathbf{X} = \{x_1, x_2, \cdots, x_N\}$を生成します。
ガウス分布に従う$N$個のデータをランダムに生成します。
# (観測)データ数を指定 N = 50 # ガウス分布に従うデータを生成 x_n = np.random.normal(loc=mu_truth, scale=np.sqrt(1 / lambda_truth), size=N)
生成するデータ数$N$をNとして値を指定します。
ガウス分布に従う乱数は、np.random.normal()で生成できます。平均の引数locにmu_truth、標準偏差の引数scaleにnp.sqrt(1 / lambda_truth)、試行回数の引数sizeにNを指定します。生成したN個のデータをx_nとします。
観測したデータを確認しましょう。
# 観測データを確認 print(x_n[:5])
[ 8.41432049 31.20767259 23.97417915 27.46498765 32.89933337]
観測データをヒストグラムでも確認します。
# 観測データのヒストグラムを作図 plt.figure(figsize=(12, 9)) plt.hist(x=x_n, bins=50) # 観測データ plt.xlabel('x') plt.ylabel('count') plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('$N=' + str(N) + ', \mu=' + str(mu_truth) + ', \sigma=' + str(np.sqrt(1 / lambda_truth)) + '$', loc='left') plt.show()
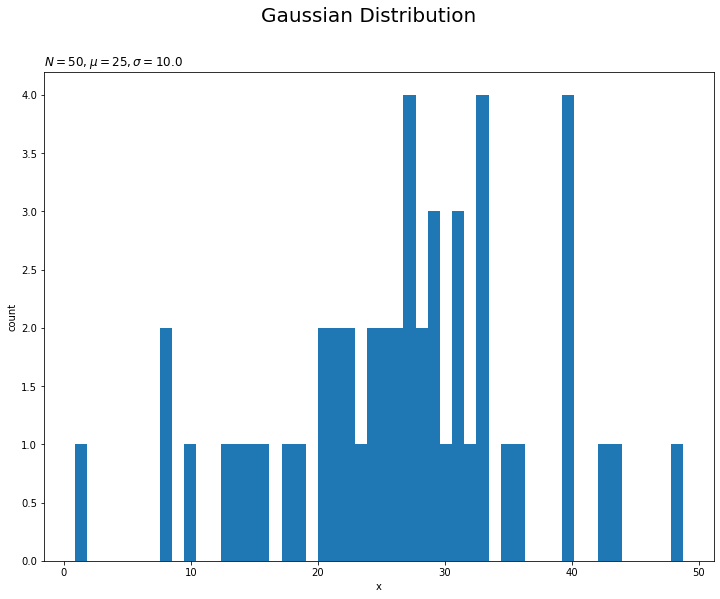
データ数が十分に大きいと、分布の形状が真の分布に近づきます。
・事前分布の設定
次に、尤度に対する共役事前分布を設定します。
$\mu$の事前分布(ガウス分布)のパラメータ(超パラメータ)を設定します。
# muの事前分布のパラメータを指定 m = 0 beta = 1
ガウス分布の平均パラメータ$m$と精度パラメータの係数$\beta$をそれぞれm, betaとして値を指定します。
また、$\lambda$の事前分布(ガンマ分布)のパラメータ(超パラメータ)を設定します。
# lambdaの事前分布のパラメータを指定 a = 1 b = 1
ガンマ分布のパラメータ$a,\ b$をそれぞれa, bとして正の実数値を指定します。
$\mu$の事前分布の計算用に、$\lambda$の事前分布から$\lambda$の期待値を求めます。
# lambdaの期待値を計算:式(2.59)
E_lambda = a / b
ガンマ分布の期待値は
で計算します。
設定したパラメータを使って、$\mu$の事前分布の確率密度を計算します。
# 作図用のmuの値を設定 mu_line = np.linspace(mu_truth - 50, mu_truth + 50, num=1000) # muの事前分布を計算:式(2.64) ln_C_N = - 0.5 * (np.log(2 * np.pi) - np.log(beta * E_lambda)) # 正規化項(対数) prior_mu = np.exp(ln_C_N - 0.5 * beta * E_lambda * (mu_line - m)**2) # 確率密度 # muの事前分布を計算:SciPy ver #prior_mu = norm.pdf(x=mu_line, loc=m, scale=np.sqrt(1 / beta / E_lambda)) # 確率密度
作図用に、ガウス分布に従う変数$\mu$がとり得る値をnp.linspace()で作成してmu_lineとします。この例では、真の値を中心に指定した範囲とします(本当は自動で良い感じの範囲になるようにしたかった)。
尤度のときと同様にして、確率密度を計算します。
計算結果は次のようになります。
# 確認 print(prior_mu[:10])
[7.65392974e-137 9.30104353e-136 1.11899266e-134 1.33281895e-133
1.57167749e-132 1.83486477e-131 2.12076746e-130 2.42677992e-129
2.74926177e-128 3.08354399e-127]
$\mu$の事前分布を作図します。
# muの事前分布を作図 plt.figure(figsize=(12, 9)) plt.plot(mu_line, prior_mu, label='$\mu$ prior', color='purple') # muの事前分布 plt.xlabel('$\mu$') plt.ylabel('density') plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('$m=' + str(m) + ', \\beta=' + str(beta) + ', E[\lambda]=' + str(np.round(E_lambda, 3)) + '$', loc='left') plt.show()
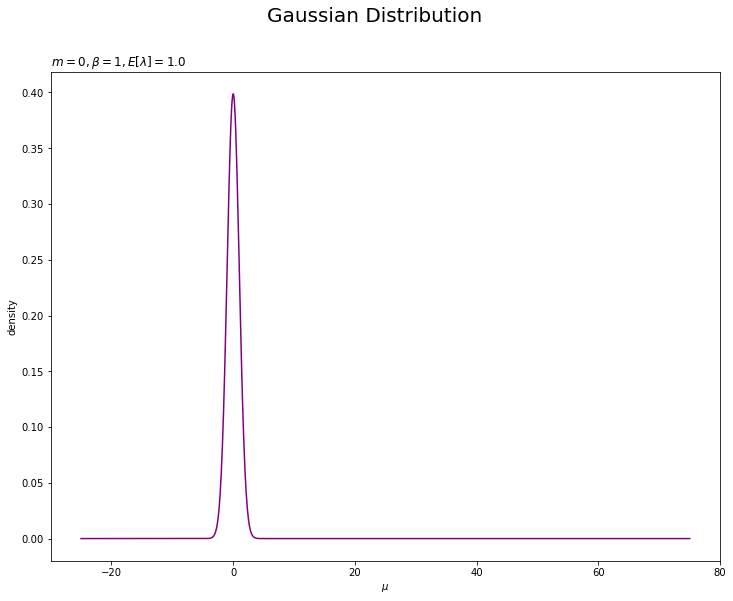
m, betaやa, bの値を変更することで、ガウス分布におけるパラメータと形状の関係を確認できます。
続いて、$\lambda$の事前分布の確率密度も計算します。
# 作図用のlambdaの値を設定 lambda_line = np.linspace(0, 4 * lambda_truth, num=1000) # lambdaの事前分布を計算:式(2.56) ln_C_Gam = a * np.log(b) - math.lgamma(a) # 正規化項(対数) prior_lambda = np.exp(ln_C_Gam + (a - 1) * np.log(lambda_line) - b * lambda_line) # 確率密度 # lambdaの事前分布を計算:SciPy ver #prior_lambda = gamma.pdf(x=lambda_line, a=a, scale=1 / b) # 確率密度
作図用に、ガンマ分布に従う変数$\lambda$がとり得る値をnp.linspace()で作成してlambda_lineとします。この例では、0から真の値の4倍までを範囲とします。
lambda_lineの値ごとに確率密度を計算します。ガンマ分布の確率密度は、対数をとった定義式
で計算して、最後にnp.exp()をします。ここで、$\Gamma(\cdot)$はガンマ関数です。
ガンマ関数の計算はmath.gamma()で行えますが、値が大きくなると発散してしまします。そこで、対数をとったガンマ関数math.lgamma()で計算した後にnp.exp()で戻します。
ガンマ分布の確率密度は、scipy.statsのgamma.pdf()でも計算できます。
計算結果は次のようになります。
# 確認 print(lambda_line[:10]) print(prior_lambda[:10])
[0.00000000e+00 4.00400400e-05 8.00800801e-05 1.20120120e-04
1.60160160e-04 2.00200200e-04 2.40240240e-04 2.80280280e-04
3.20320320e-04 3.60360360e-04]
[ nan 0.99995996 0.99991992 0.99987989 0.99983985 0.99979982
0.99975979 0.99971976 0.99967973 0.9996397 ]
np.log(0)が-Infになります。
$\lambda$の事前分布を作図します。
# lambdaの事前分布を作図 plt.figure(figsize=(12, 9)) plt.plot(lambda_line, prior_lambda, label='$\lambda$ prior', color='purple') # lambdaの事前分布 plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution', fontsize=20) plt.title('$a=' + str(a) + ', b=' + str(b) + '$', loc='left') plt.show()

(lambda_lineの範囲をもっと広くして)a, bの値を変更することで、ガウス分布におけるパラメータと形状の関係を確認できます。
・事後分布の計算
観測データ$\mathbf{X}$からパラメータ$\lambda$の事後分布を求めます(パラメータ$\lambda$を分布推定します)。
観測データx_nを用いて、$\mu$の事後分布(ガウス分布)のパラメータを計算します。
# muの事後分布のパラメータを計算:式(3.83)
beta_hat = N + beta
m_hat = (np.sum(x_n) + beta * m) / beta_hat
$\mu$の事後分布のパラメータは
で計算して、結果をbeta_hat, m_hatとします。
# 確認 print(beta_hat) print(m_hat)
51
26.05737173276807
続いて、$\lambda$の事後分布(ガンマ分布)のパラメータも計算します。
# lambdaの事後分布のパラメータを計算:式(3.88) a_hat = 0.5 * N + a b_hat = 0.5 * (np.sum(x_n**2) + beta * m**2 - beta_hat * m_hat**2) + b
$\lambda$の事後分布のパラメータは
で計算して、結果をa_hat, b_hatとします。
# 確認 print(a_hat) print(b_hat)
26.0
2724.0277386702037
$\mu$の事後分布の計算用に、$\lambda$の事後分布から$\hat{\lambda}$の期待値を求めます。
# lambdaの期待値を計算:式(2.59) E_lambda_hat = a_hat / b_hat # 確認 print(E_lambda_hat)
0.009544689883625229
求めたパラメータを使って、$\mu$の事後分布の確率密度を計算します。
# muの事後分布を計算:式(2.64) ln_C_N = - 0.5 * (np.log(2 * np.pi) - np.log(beta_hat * E_lambda_hat)) # 正規化項(対数) posterior_mu = np.exp(ln_C_N - 0.5 * beta_hat * E_lambda_hat * (mu_line - m_hat)**2) # 確率密度 # muの事前分布を計算:SciPy ver #posterior_mu = norm.pdf(x=mu_line, loc=m_hat, scale=np.sqrt(1 / beta_hat / E_lambda_hat)) # 確率密度
更新した超パラメータm_hat, lambda_mu_hatを用いて、事前分布のときと同様にして計算します。
計算結果は次のようになります。
# 確認 print(posterior_mu[:10])
[7.81257223e-277 9.37985990e-276 1.12067676e-274 1.33243519e-273
1.57649839e-272 1.85619107e-271 2.17487117e-270 2.53586485e-269
2.94239100e-268 3.39747580e-267]
$\mu$の事後分布を作図します。
# muの事後分布を作図 plt.figure(figsize=(12, 9)) plt.plot(mu_line, posterior_mu, label='$\mu$ posterior', color='purple') # muの事後分布 plt.vlines(x=mu_truth, ymin=0, ymax=max(posterior_mu), label='$\mu$ truth', color='red', linestyle='--') # 真のmu plt.xlabel('$\mu$') plt.ylabel('density') plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('$N=' + str(N) + ', \hat{m}=' + str(np.round(m_hat, 1)) + ', \hat{\\beta}=' + str(beta_hat) + ', E[\hat{\lambda}]=' + str(np.round(E_lambda_hat, 3)) + '$', loc='left') plt.legend() plt.show()
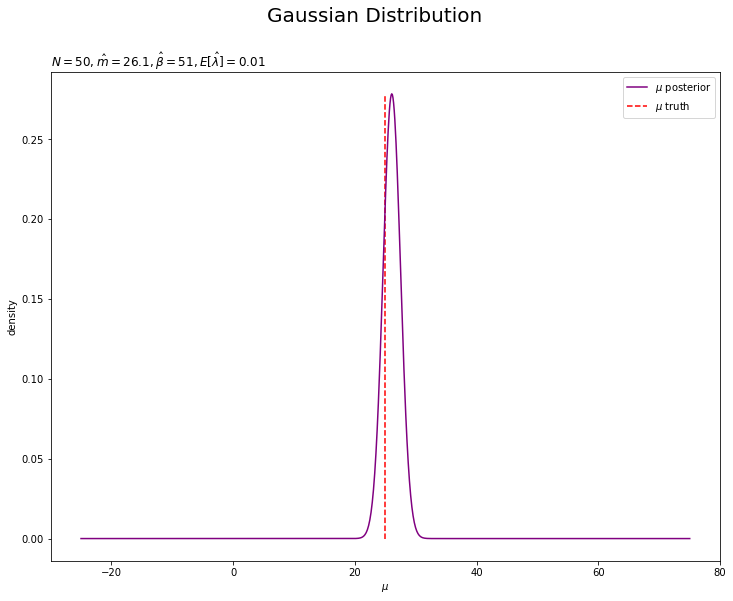
パラメータ$\mu$の真の値付近をピークとする分布を推定できています。
続いて、$\lambda$の事後分布の確率密度も計算します。
# lambdaの事後分布の計算:式(2.56) ln_C_Gam = a_hat * np.log(b_hat) - math.lgamma(a_hat) # 正規化項(対数) posterior_lambda = np.exp(ln_C_Gam + (a_hat - 1) * np.log(lambda_line) - b_hat * lambda_line) # 確率密度 # lambdaの事前分布を計算:SciPy ver #posterior_lambda = gamma.pdf(x=lambda_line, a=a_hat, scale=1 / b_hat) # 確率密度
更新した超パラメータa_hat, b_hatを用いて、事前分布のときと同様にして計算します。
計算結果は次のようになります。
# 確認 print(posterior_lambda[:10])
[0.00000000e+00 1.37990119e-46 4.15173192e-39 9.40031058e-35
1.12006194e-31 2.65842118e-29 2.27397854e-27 9.61806098e-26
2.42950403e-24 4.13963554e-23]
$\lambda$の事後分布を作図します。
# lambdaの事後分布を作図 plt.figure(figsize=(12, 9)) plt.plot(lambda_line, posterior_lambda, label='$\lambda$ posterior', color='purple') # lambdaの事後分布 plt.vlines(x=lambda_truth, ymin=0, ymax=max(posterior_lambda), label='$\lambda$ truth', color='red', linestyle='--') # 真のlambda plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution', fontsize=20) plt.title('$N=' + str(N) + ', a=' + str(a_hat) + ', b=' + str(np.round(b_hat, 1)) + '$', loc='left') plt.legend() plt.show()
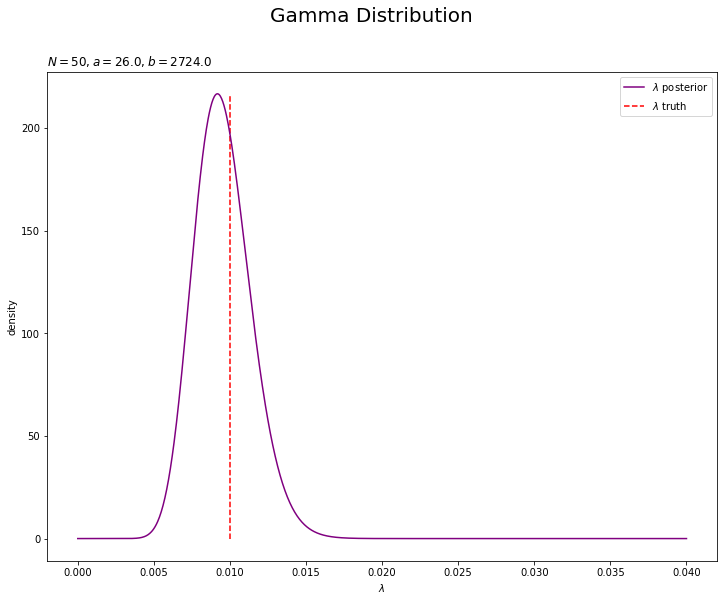
パラメータ$\lambda$の真の値付近をピークとする分布を推定できています。
・予測分布の計算
最後に、観測データ$\mathbf{X}$から未観測のデータ$x_{*}$の予測分布を求めます。
$\mu$の事後分布のパラメータm_hat, beta_hatと$\lambda$の事後分布のパラメータa_hat, b_hat、または観測データx_nと$\mu$の事前分布のパラメータm, beta、$\lambda$の事前分布のパラメータa, bを用いて、予測分布(スチューデントのt分布)のパラメータを計算します。
# 予測分布のパラメータを計算:式(3.95') mu_s_hat = m_hat lambda_s_hat = beta_hat * a_hat / (1 + beta_hat) / b_hat nu_s_hat = 2 * a_hat mu_s_hat = (np.sum(x_n) + beta_hat * m) / (N + beta) # 予測分布のパラメータを計算:式(3.95') #numer_lambda = (N + beta) * (0.5 * N + a) #denom_lambda = (N + 1 + beta) * (0.5 * (np.sum(x_n**2) + beta + m**2 - beta_hat * m_hat**2) + beta) #lambda_s_hat = numer_lambda / denom_lambda #nu_s_hat = N + 2 * a
予測分布のパラメータは
で計算して、結果をmu_s_hat, lambda_s_hat, nu_s_hatとします。$\mu_s$は平均、$\lambda_s$は何?、$\nu_s$は自由度です。
それぞれ上の式だと、事後分布のパラメータmu_hat, beta_hat、a_hat, b_hatを使って計算できます。下の式だと、観測データx_nと事前分布のパラメータmu, beta、a, bを使って計算できます(嘘ですね$\hat{\beta}$と$\hat{m}$が残ってますねでもめんどいよう…)。
# 確認 print(mu_s_hat) print(lambda_s_hat) print(nu_s_hat)
26.05737173276807
0.009361138155093974
52.0
$\mathbf{X}$から$\hat{\mu}_s,\ \hat{\lambda}_s,\ \hat{\nu}_s$を学習しているのが式からも分かります。
求めたパラメータを使って、予測分布を計算します。
# 予測分布を計算:式(3.76) ln_C_St = math.lgamma(0.5 * (nu_s_hat + 1)) - math.lgamma(0.5 * nu_s_hat) # 正規化項(対数) ln_term1 = 0.5 * np.log(lambda_s_hat / np.pi / nu_s_hat) ln_term2 = - 0.5 * (nu_s_hat + 1) * np.log(1 + lambda_s_hat / nu_s_hat * (x_line - mu_s_hat)**2) predict = np.exp(ln_C_St + ln_term1 + ln_term2) # 確率密度 # 予測分布を計算:SciPy ver predict = t.pdf(x=x_line, df=nu_s_hat, loc=mu_s_hat, scale=np.sqrt(1 / lambda_s_hat))
x_lineの値ごとに確率密度を計算します。1次元スチューデントのt分布の確率密度は、対数をとった定義式
で計算して、最後にnp.exp()をします。この$\pi$は円周率です。
ガンマ分布の確率密度は、scipy.statsのt.pdf()でも計算できます。
計算結果は次のようになります。
# 確認 print(predict[:10])
[3.42262543e-05 3.50595213e-05 3.59121709e-05 3.67846278e-05
3.76773252e-05 3.85907051e-05 3.95252184e-05 4.04813249e-05
4.14594937e-05 4.24602034e-05]
予測分布を尤度と重ねて作図します。
# 予測分布を作図 plt.figure(figsize=(12, 9)) plt.plot(x_line, predict, label='predict', color='purple') # 予測分布 plt.plot(x_line, true_model, label='true', color='red', linestyle='--') # 真の分布 plt.xlabel('x') plt.ylabel('density') plt.suptitle("Student's t Distribution", fontsize=20) plt.title('$N=' + str(N) + ', \hat{\mu}_s=' + str(np.round(mu_s_hat, 1)) + ', \hat{\lambda}_s=' + str(np.round(lambda_s_hat, 3)) + ', \hat{\\nu}_s=' + str(nu_s_hat) + '$', loc='left') plt.legend() plt.show()
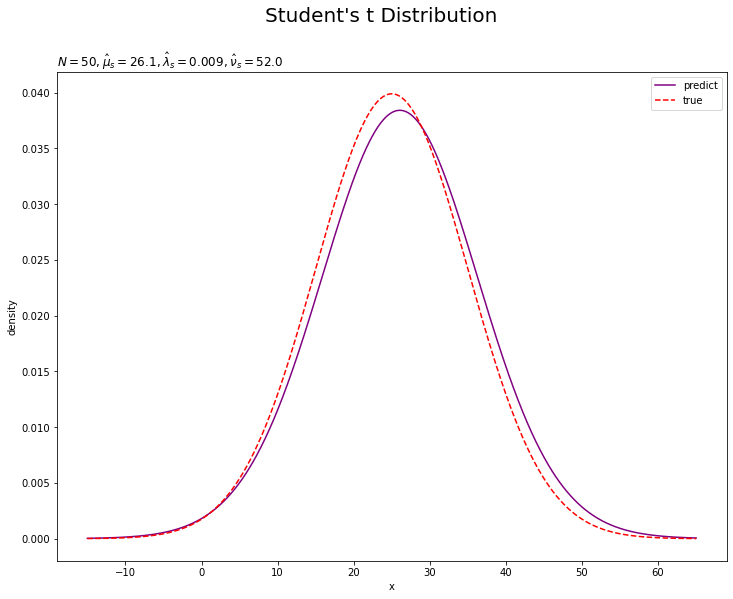
観測データが増えると、予測分布が真の分布に近づきます。
・おまけ:アニメーションで推移の確認
animationモジュールを利用して、事後分布と予測分布の推移をアニメーション(gif画像)で確認するためのコードです。
・コード(クリックで展開)
異なる点のみを簡単に解説します。
# 利用するライブラリ import numpy as np from scipy.stats import norm, gamma, t # 1次元ガウス分布, ガンマ分布, 1次元スチューデントのt分布 import matplotlib.pyplot as plt import matplotlib.animation as animation
・モデルの設定
# 真のパラメータを指定 mu_truth = 25 lambda_truth = 0.01 # muの事前分布のパラメータを指定 m = 0 beta = 1 # lambdaの事前分布のパラメータを指定 a = 1 b = 1 # lambdaの期待値を計算:式(2.59) E_lambda = a / b # 初期値による予測分布のパラメータを計算:式(3.95) mu_s = m lambda_s = beta * a / (1 + beta) / b nu_s = 2 * a # 作図用のxの値を設定 x_line = np.linspace( mu_truth - 4 * np.sqrt(1 / lambda_truth), mu_truth + 4 * np.sqrt(1 / lambda_truth), num=1000 ) # 作図用のmuの値を設定 mu_line = np.linspace(mu_truth - 50, mu_truth + 50, num=1000) # 作図用のlambdaの値を設定 lambda_line = np.linspace(0, 4 * lambda_truth, num=1000)
・推論処理
各試行の結果をリストに格納していく必要があります。$\mu$の事後分布をtrace_posterior_mu、$\lambda$の事後分布をtrace_posterior_lambda、予測分布をtrace_predict、パラメータについてもそれぞれtrace_***として、初期値の結果を持つように作成しておきます。
# データ数(試行回数)を指定 N = 100 # 推移の記録用の受け皿を初期化 x_n = np.empty(N) trace_m = [m] trace_beta = [beta] trace_posterior_mu = [norm.pdf(x=mu_line, loc=m, scale=np.sqrt(1 / beta / E_lambda))] trace_a = [a] trace_b = [b] trace_posterior_lambda = [gamma.pdf(x=lambda_line, a=a, scale=1 / b)] trace_mu_s = [mu_s] trace_lambda_s = [lambda_s] trace_nu_s = [nu_s] trace_predict = [t.pdf(x=x_line, df=nu_s, loc=mu_s, scale=np.sqrt(1 / lambda_s))] # ベイズ推論 for n in range(N): # ガウス分布に従うデータを生成 x_n[n] = np.random.normal(loc=mu_truth, scale=np.sqrt(1 / lambda_truth), size=1) # muの事後分布のパラメータを更新:式(3.83) old_beta = beta old_m = m beta += 1 m = (x_n[n] + old_beta * m) / beta # lambdaの事後分布のパラメータを更新:式(3.88) a += 0.5 b += 0.5 * (x_n[n]**2 + old_beta * old_m**2 - beta * m**2) # lambdaの期待値を計算:式(2.59) E_lambda = a / b # muの事前分布を計算:式(2.64) trace_posterior_mu.append( norm.pdf(x=mu_line, loc=m, scale=np.sqrt(1 / beta / E_lambda)) ) # lambdaの事前分布を計算:式(2.56) trace_posterior_lambda.append(gamma.pdf(x=lambda_line, a=a, scale=1 / b)) # 予測分布のパラメータを更新:式(3.95) mu_s = m lambda_s = beta * a / (1 + beta) / b nu_s = 2 * a # 予測分布を計算:式(3.76) trace_predict.append(t.pdf(x=x_line, df=nu_s, loc=mu_s, scale=np.sqrt(1 / lambda_s))) # 超パラメータを記録 trace_m.append(m) trace_beta.append(beta) trace_a.append(a) trace_b.append(b) trace_mu_s.append(mu_s) trace_lambda_s.append(lambda_s) trace_nu_s.append(nu_s)
観測された各データによってどのように学習する(分布が変化する)のかを確認するため、for文で1データずつ処理します。よって、データ数Nがイタレーション数になります。
超パラメータに関して、$\hat{m},\ \hat{\beta}$に対応するm_hat, beta_hatや$\hat{a},\ \hat{b}$に対応するa_hat, b_hatを新たに作るのではなく、m_hat, beta_hatとa, bをイタレーションごとに更新(上書き)していきます。
それに伴い、事後分布のパラメータの計算式(3.83)(3.88)の$\sum_{n=1}^N x_n$や$N$といった計算は、ループ処理によってN回繰り返しx_n[n]や1を加えることで行います。n回目のループ処理のときには、n-1回分のx_n[n]や1が既に各パラメータに加えられているわけです。
・$\mu$の事後分布の推移
# 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_posterior_mu(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目のmuの事後分布を作図 plt.plot(mu_line, trace_posterior_mu[n], label='$\mu$ posterior', color='purple') # muの事後分布 plt.vlines(x=mu_truth, ymin=0, ymax=np.nanmax(trace_posterior_mu), label='$\mu$ trurh', color='red', linestyle='--') # 真のmu plt.xlabel('$\mu$') plt.ylabel('density') plt.suptitle('Gaussian Distribution', fontsize=20) plt.title('$N=' + str(n) + ', \hat{m}=' + str(np.round(trace_m[n], 1)) + ', \hat{\\beta}=' + str(trace_beta[n]) + '$', loc='left') plt.legend() # gif画像を作成 posterior_anime = animation.FuncAnimation(fig, update_posterior_mu, frames=N + 1, interval=100) posterior_anime.save("ch3_3_3_Posterior_mu.gif")
初期値(事前分布)を含むため、フレーム数の引数framesはN + 1です。
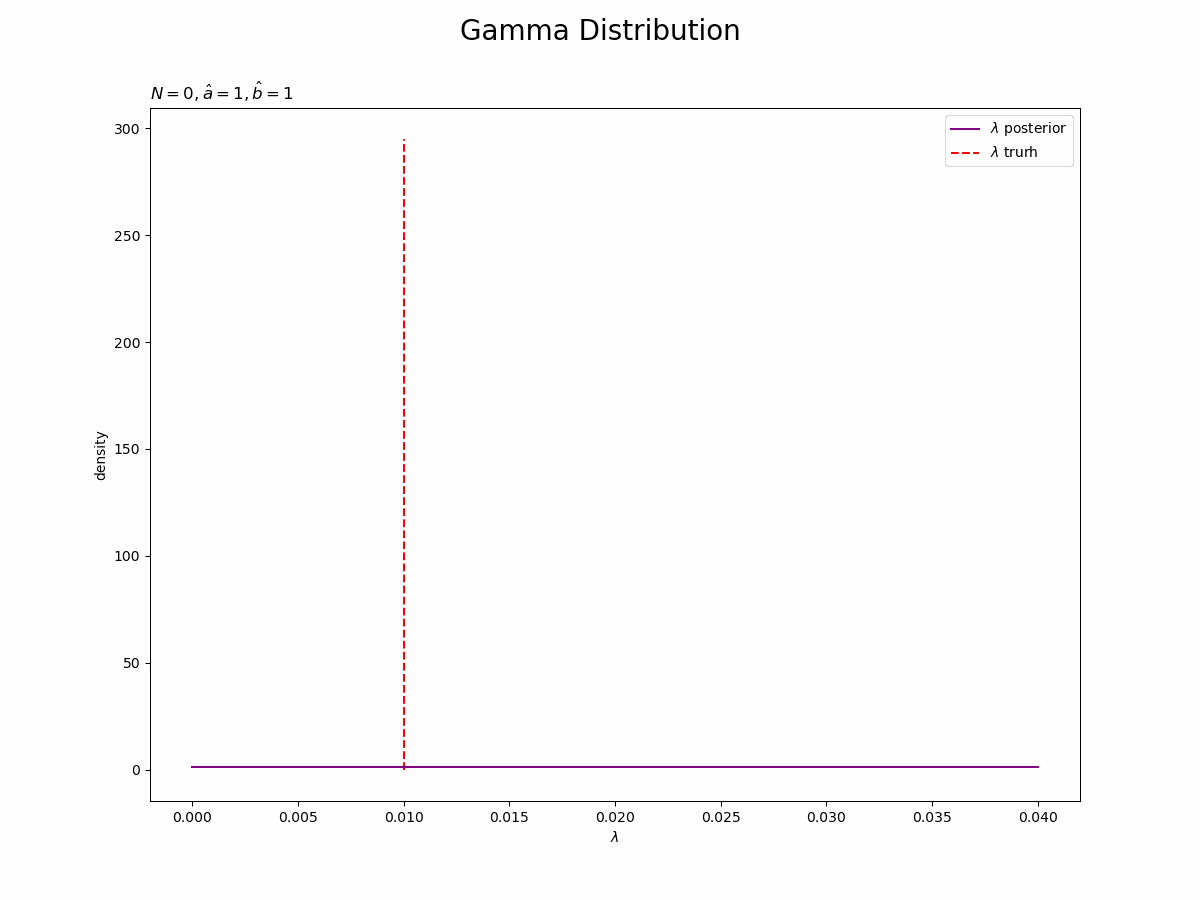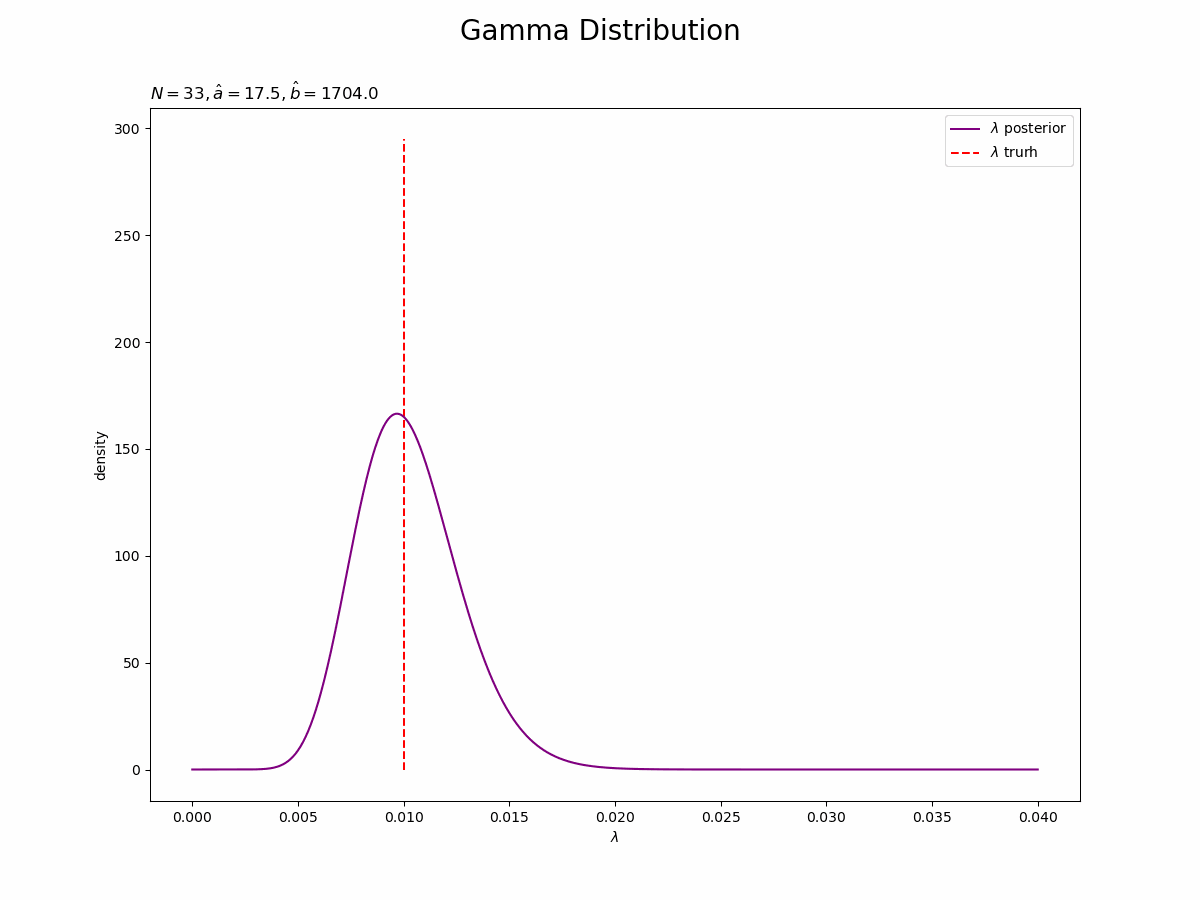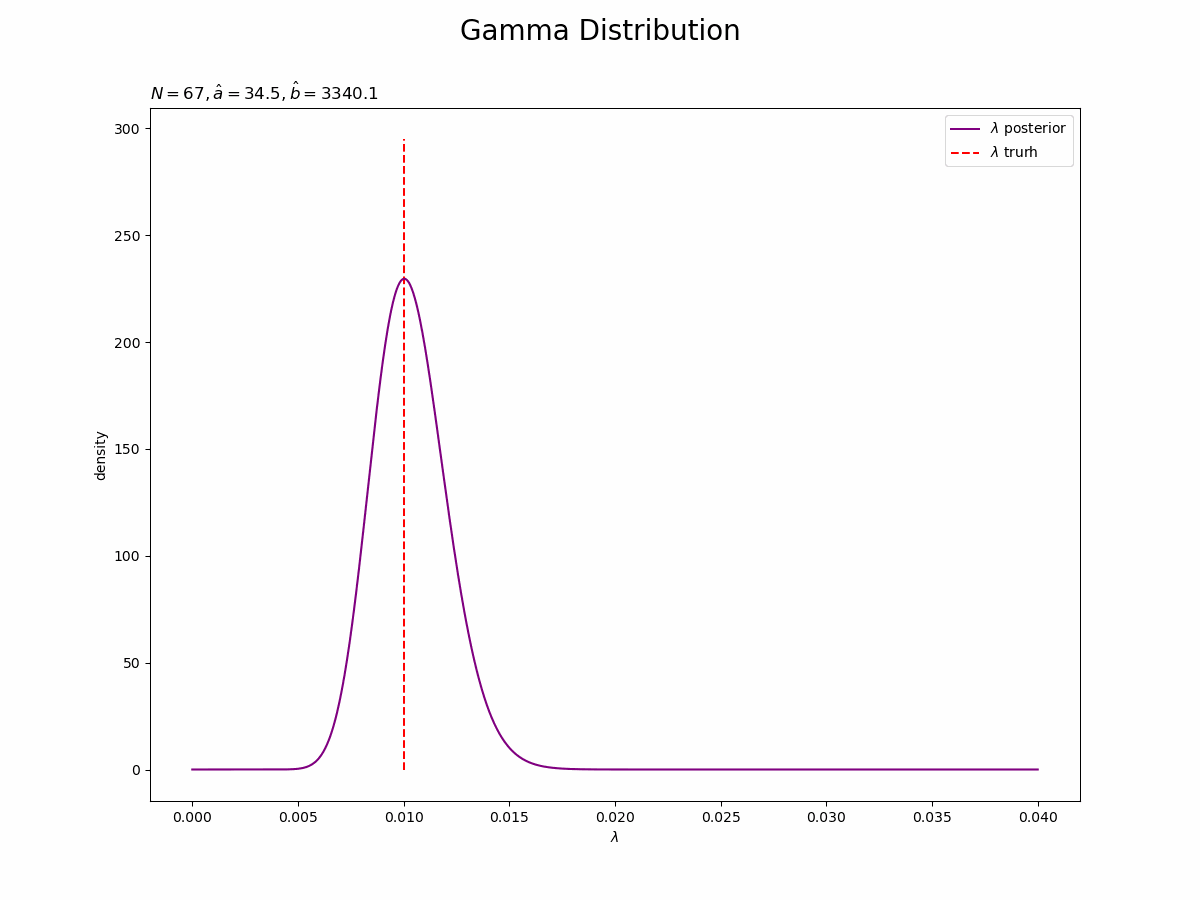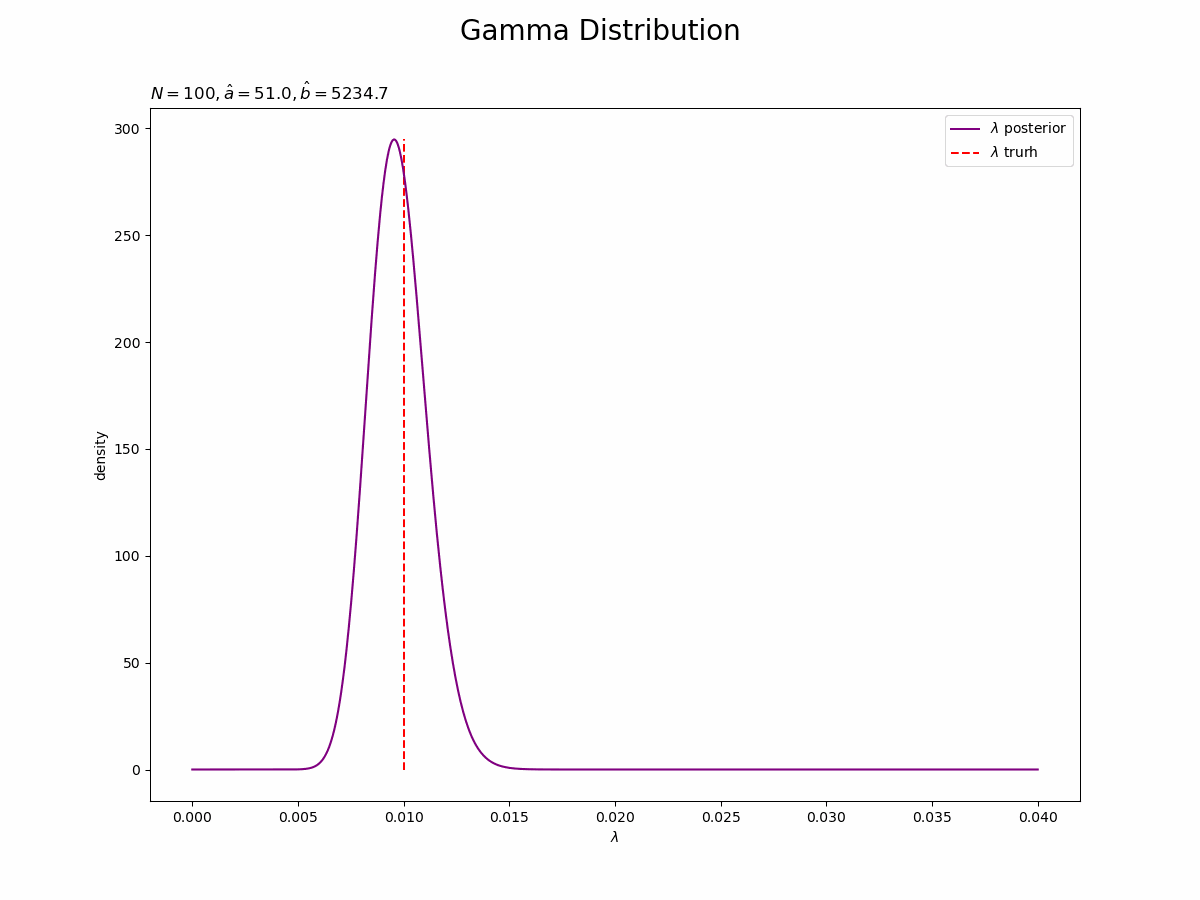
・$\lambda$の事後分布の推移
## lambdaの事後分布の推移をgif画像化 # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_posterior_lambda(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目のlambdaの事後分布を作図 plt.plot(lambda_line, trace_posterior_lambda[n], label='$\lambda$ posterior', color='purple') # lambdaの事後分布 plt.vlines(x=lambda_truth, ymin=0, ymax=np.nanmax(trace_posterior_lambda), label='$\lambda$ trurh', color='red', linestyle='--') # 真のlambda plt.xlabel('$\lambda$') plt.ylabel('density') plt.suptitle('Gamma Distribution', fontsize=20) plt.title('$N=' + str(n) + ', \hat{a}=' + str(trace_a[n]) + ', \hat{b}=' + str(np.round(trace_b[n], 1)) + '$', loc='left') plt.legend() # gif画像を作成 posterior_anime = animation.FuncAnimation(fig, update_posterior_lambda, frames=N + 1, interval=100) posterior_anime.save("ch3_3_3_Posterior_lambda.gif")
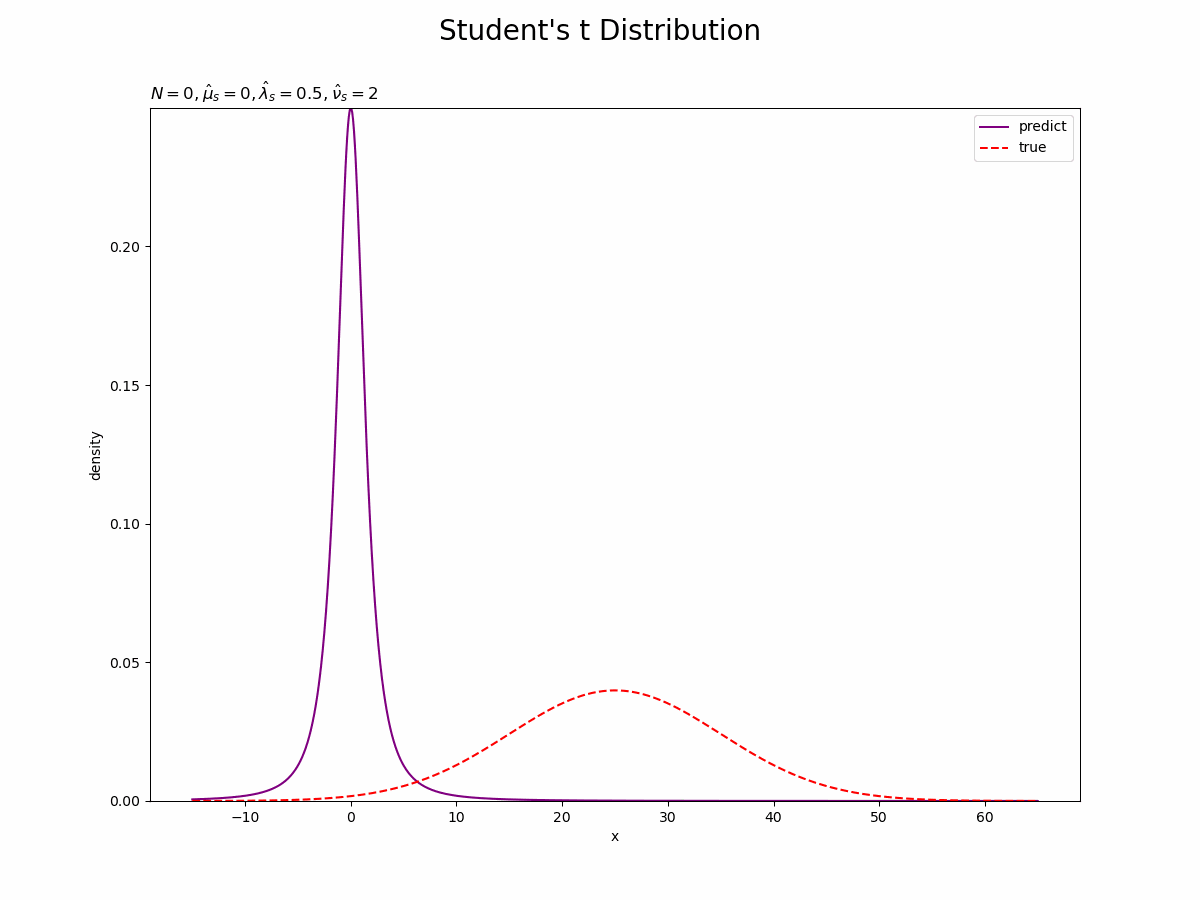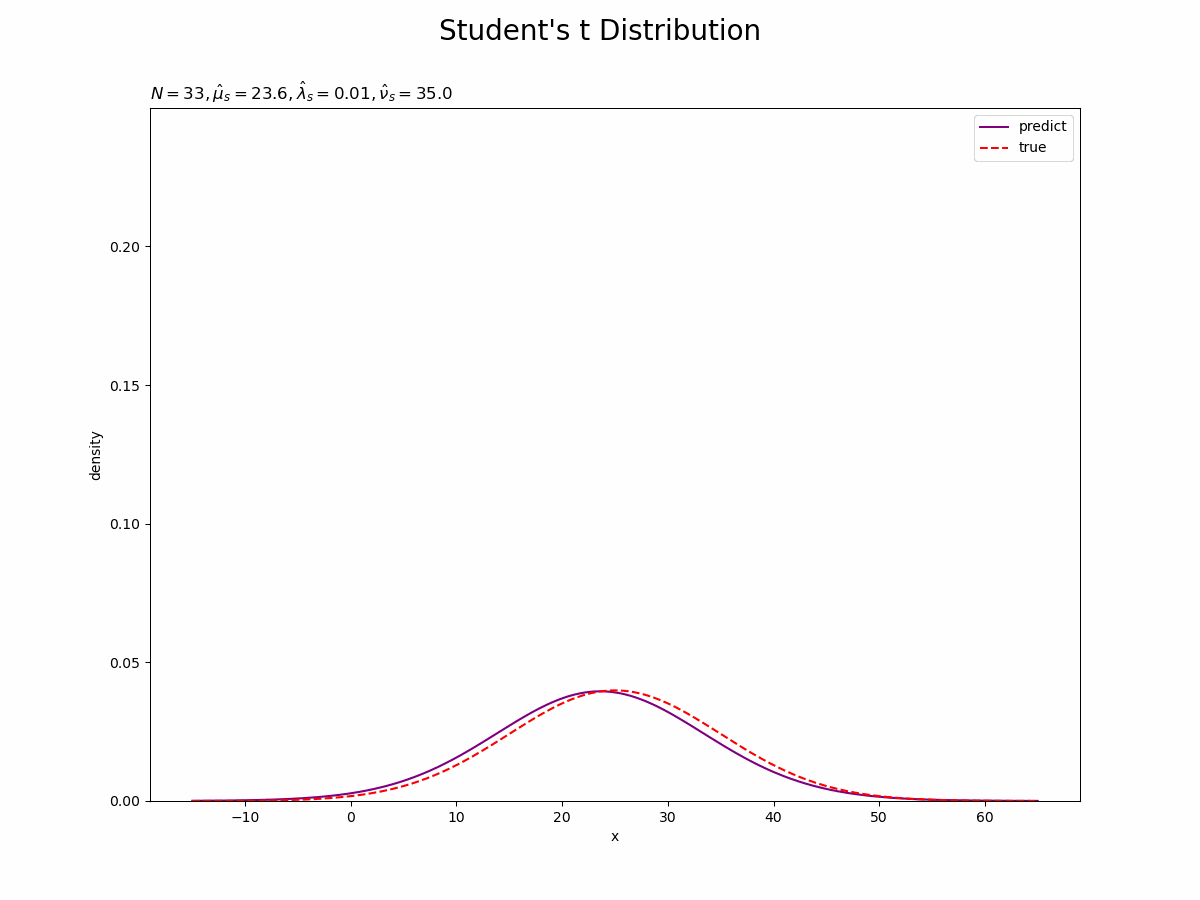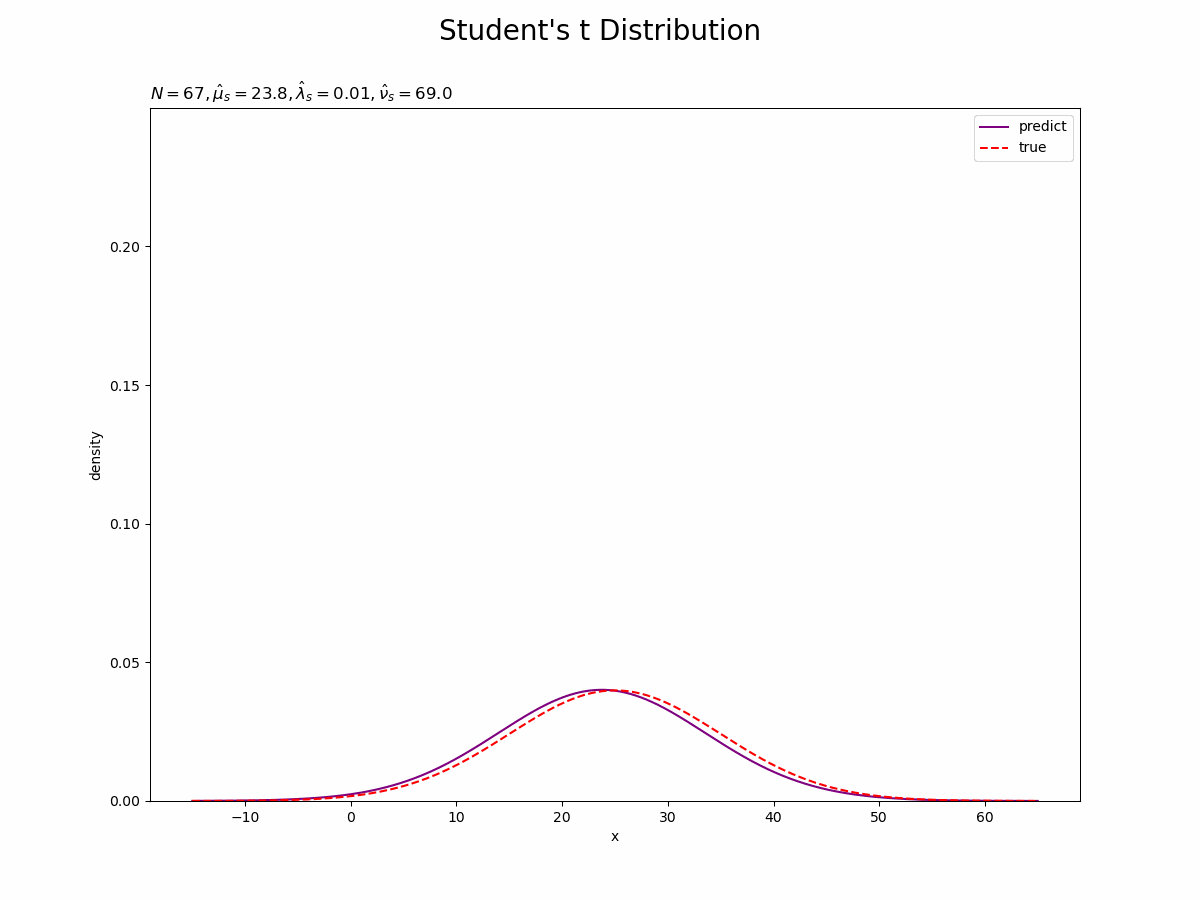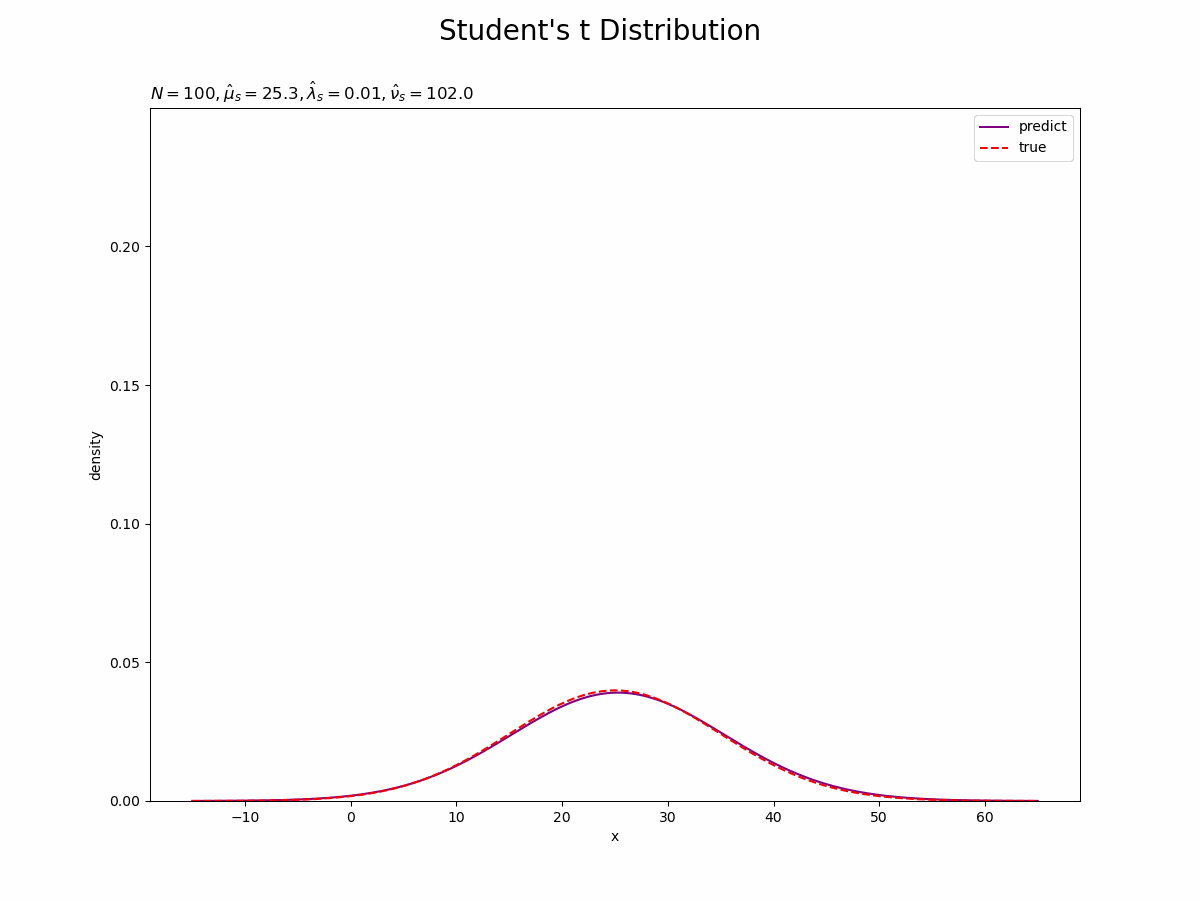
・予測分布の推移
# 尤度を計算:式(2.64) true_model = norm.pdf(x=x_line, loc=mu_truth, scale=np.sqrt(1 / lambda_truth)) # 確率密度 # 画像サイズを指定 fig = plt.figure(figsize=(12, 9)) # 作図処理を関数として定義 def update_predict(n): # 前フレームのグラフを初期化 plt.cla() # nフレーム目の予測分布を作図 plt.plot(x_line, trace_predict[n], label='predict', color='purple') # 予測分布 plt.plot(x_line, true_model, label='true', color='red', linestyle='--') # 真の分布 plt.xlabel('x') plt.ylabel('density') plt.suptitle("Student's t Distribution", fontsize=20) plt.title('$N=' + str(n) + ', \hat{\mu}_s=' + str(np.round(trace_mu_s[n], 1)) + ', \hat{\lambda}_s=' + str(np.round(trace_lambda_s[n], 3)) + ', \hat{\\nu}_s=' + str(trace_nu_s[n]) + '$', loc='left') plt.ylim(0, np.nanmax(trace_predict)) plt.legend() # gif画像を作成 predict_anime = animation.FuncAnimation(fig, update_predict, frames=N + 1, interval=100) predict_anime.save("ch3_3_3_Predict.gif")
(よく理解していないので、animationの解説は省略…とりあえずこれで動きます……)

参考文献
- 須山敦志『ベイズ推論による機械学習入門』(機械学習スタートアップシリーズ)杉山将監修,講談社,2017年.
おわりに
3章の実装編はこれで完了です!私はこれから3章の数式読解編の復習・修正作業に入ります。
【次節の内容】