はじめに
『ゼロからできるMCMC』の図とサンプルコードをR言語で再現します。本と一緒に読んでください。
この記事は、4章の内容です。マルコフ連鎖モンテカルロ法の1つであるメトロポリス法を行います。
【前の章の内容】
【他の章の内容】
【この章の内容】
この章で利用するパッケージを読み込みます。
# 利用パッケージ library(tidyverse) library(gganimate)
gganimateパッケージは、gif画像を作成するパッケージです。推移をアニメーションで確認するのに使います。
4.1 メトロポリス法
次のような式の形状の確率分布を考えます。
これまで扱ってきた(平均$\mu = 0$、標準偏差$\sigma = 1$の)ガウス分布もこの形状の確率分布です。
式(4.1)の$S(x)$を作用または負の対数尤度と呼び、$\exp(\cdot)$の部分の対数をとり符号を反転させたものです(本当は$- \log P(x)$のことだったりしない?)。$\log [\exp(x)] = x$という性質から、式(1)の場合は
となります。
$Z$を規格化因子や正規化項と呼び、3章でも少し触れましたが、$\exp(\cdot)$の部分を積分したものです。
$\frac{1}{Z}$には、確率分布を積分したときに1になるようにする働きがあります。
・指数関数
続いて、指数関数$\exp(x)$の性質を確認しておきましょう。この資料では、$e^x$を$\exp(x)$と表記することにします。$e$はネイピア数です。
# 指数関数のグラフをプロット tibble( x = seq(-2, 2, 0.01), exp_x = exp(x) ) %>% ggplot(aes(x = x, y = exp_x)) + geom_line() + labs(title = expression(y == exp(x)), y = "y")
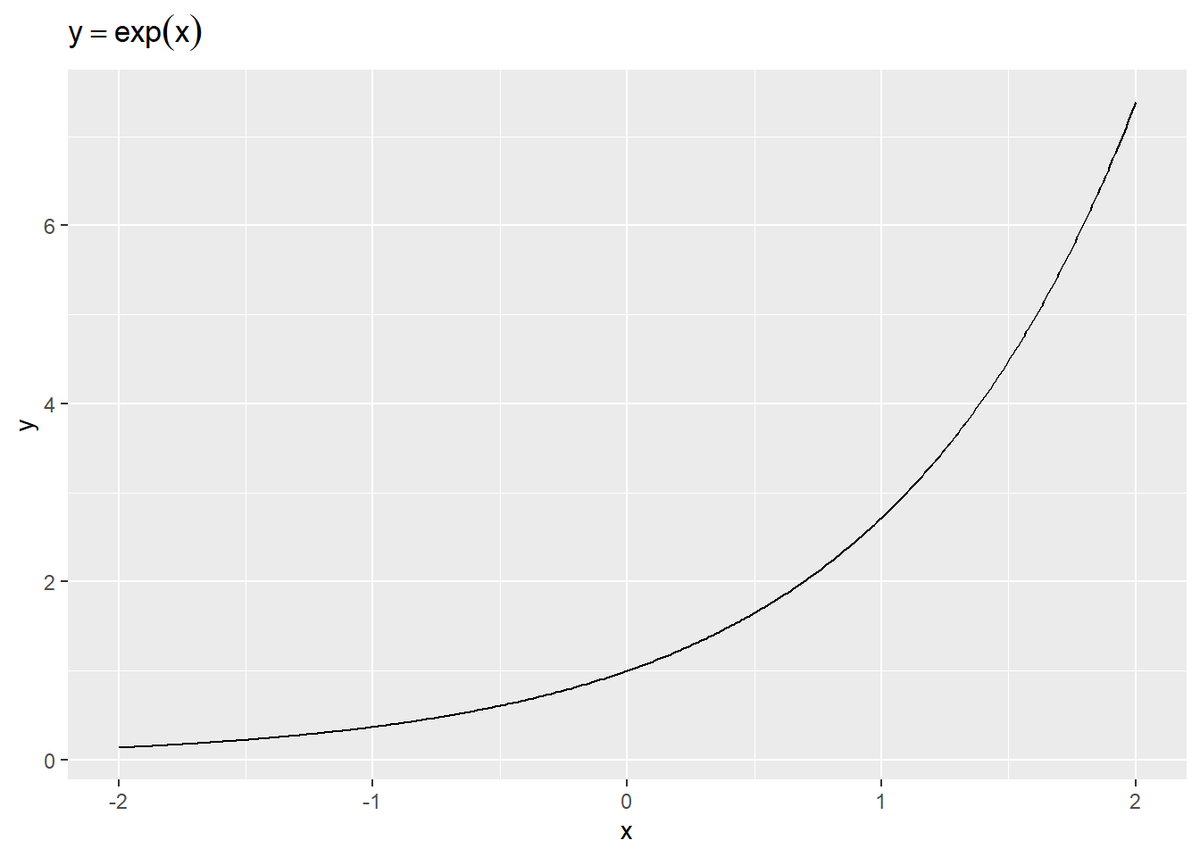
$\exp(x)$は、$x < 0$のとき0から1の値、$x = 0$のとき1、$x > 0$のとき1より大きな値をとります。
$\exp(x)$は、常に正の値になります。
この性質から$\min[1, \exp(S(x) - S(x'))]$を考えます。$\exp(S(x) - S(x'))$は、$S(x) < S(x')$のとき0から1の値(負の対数尤度って常に正だよね確か?)、$S(x) = S(x')$のとき0、$S(x) > S(x')$のとき1より大きくなります。
つまり、「現在の状態$x^{(k)}$の作用$S(x^{(k)})$」より「更新候補$x'$の作用$S(x')$」の方が大きいとき確率1で更新(必ず更新)し、小さいとき確率$\exp(S(x) - S(x'))$で更新します。
・メトロポリステスト
メトロポリス法では、0から1の一様乱数$r$を生成して、$\exp(S(x) - S(x'))$との大小関係から更新を決めます。これをメトロポリステストと呼びます。
ランダムに生成した$r$よりも$\exp(S(x) - S(x'))$が、大きければ$x'$を受理し、そうでなければ$x'$を棄却して$x^{(t)}$のままとします。
確率$\exp(S(x) - S(x')))$をpとして値を指定して、試してみましょう。受理を1、棄却を0として、確率と受理率の推移を見ましょう。
# 試行回数を指定 N <- 1000 # 確率を指定 p <- 0.7 # シミュレーション tibble( x = 1:N, bin = sample(c(0, 1), size = N, prob = c(1 - p, p), replace = TRUE), # 二項分布 met = runif(n = N, min = 0, max = 1) <= p, # メトロポリステスト rate_bin = cumsum(bin) / x, rate_met = cumsum(met) / x ) %>% ggplot(aes(x = x)) + geom_line(aes(y = rate_bin), color = "blue", alpha = 1) + # 確率に従い更新 geom_line(aes(y = rate_met), color = "#00A968", alpha = 1) + # 一様乱数rを使い更新 geom_hline(aes(yintercept = p), color = "purple", linetype = "dashed") + # 真の確率値 ylim(c(0, 1)) + labs(title = expression(r < exp(S(x) - S(x^{new}))), y = "rate")
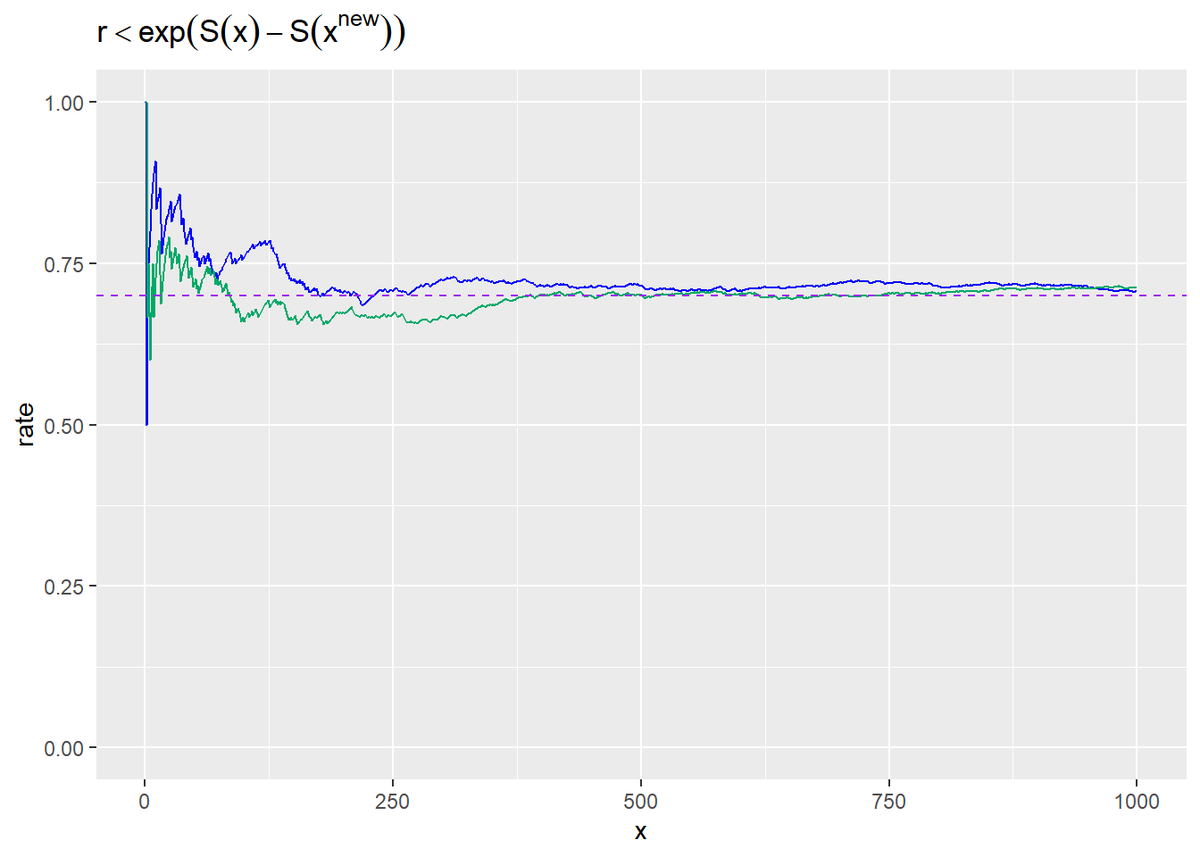
青線は、確率1-pで0、確率pで1とした場合です。緑線は、pがr以下のとき0、pがrより大きいとき1とした場合です。紫の破線が真の値です。どちらも指定した値pに収束しています。
ところで、このように一様乱数を使わなくても実装できるわけですが、なぜ一様乱数と比較する方法をとるのでしょうか?if(p > 1)の条件分岐が不要になるという良さがありそうですが、何か実装上の嬉しさや歴史的な都合があったりするのでしょうか。
メトロポリス法のキーとなる部分を確認したので、次節でメトロポリス法を行います。
4.2 期待値計算の具体例
メトロポリス法を用いて、式(1)のガウス分布による期待値を求めます。
まずは、メトロポリス法により$x$を更新していきます(サンプリングします)。初期値は$x^{(0)} = 0$とします。
# 繰り返し回数を指定 K <- 100000 # 一様乱数の範囲(ステップ幅)を指定 c <- 4 # 初期値を指定 x <- 0 # 更新推移の記録用の受け皿を作成 trace_x <- rep(0, K) n_accept <- 0 # Main loop for(k in 1:K) { # S(x)を計算 S_x <- 0.5 * x^2 # xの変化量を生成 delta_x <- runif(n = 1, min = -c, max = c) # xの更新候補を計算 dash_x <- x + delta_x # S(x')を計算 S_dash_x <- 0.5 * dash_x^2 # テスト値を生成 r <- runif(n = 1, min = 0, max = 1) # xを更新 if(r < exp(S_x - S_dash_x)) { # メトロポリステスト x <- dash_x n_accept <- n_accept + 1 } # 更新値を記録 trace_x[k] <- x } # 更新値のデータフレームを作成 update_df <- tibble( k = 1:K, x = trace_x ) # 確認 head(update_df)
## # A tibble: 6 x 2 ## k x ## <int> <dbl> ## 1 1 0 ## 2 2 0 ## 3 3 0 ## 4 4 0 ## 5 5 1.17 ## 6 6 1.50
メトロポリステスト(メトロポリス判定)r < exp(S_x - S_dash_x)がTRUEのとき、前ステップのxを候補dash_xで上書きします。
次に、得られた$x^{(1)}, \cdots, x^{(K)}$をヒストグラムで確認します。
# 真の分布を計算 true_df <- tibble( x = seq(-c, c, 0.01), # 描画範囲 P_x = exp(-x^2 / 2) / sqrt(2 * pi) # 確率密度 #P_x = dnorm(x = x, mean = 0, sd = 1) # 確率密度 ) # ヒストグラムを作成 ggplot() + geom_histogram(data = update_df, aes(x = x, y = ..density..), binwidth = 0.05) + # xのヒストグラム geom_line(data = true_df, aes(x = x, y = P_x), linetype = "dashed", color = "red") + # 真の確率密度 labs(title = "Gaussian Distribution", subtitle = paste0("K=", K, ", mu=", 0, ", sigma=", 1))
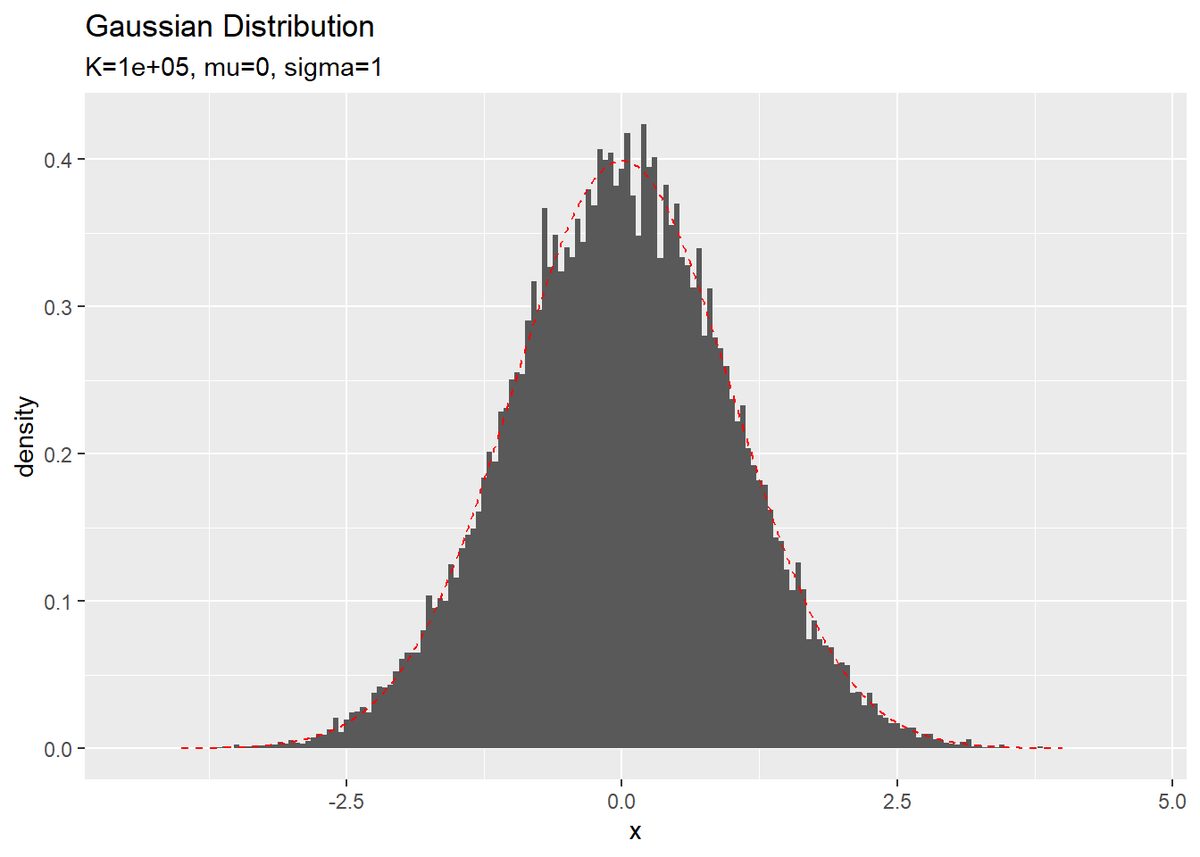
更新回数$K$が大きくなると、真の分布$P(x) = \mathcal{N}(x | \mu = 0, \sigma = 1)$に近づくのを確認できます。
更新値の推移も確認しましょう。
# 更新値の推移をグラフ化 update_df %>% filter(k >= 1, k <= 2000) %>% # 表示範囲を指定 ggplot(aes(x = k, y = x)) + geom_line() + labs(title = "Metropolis Method")
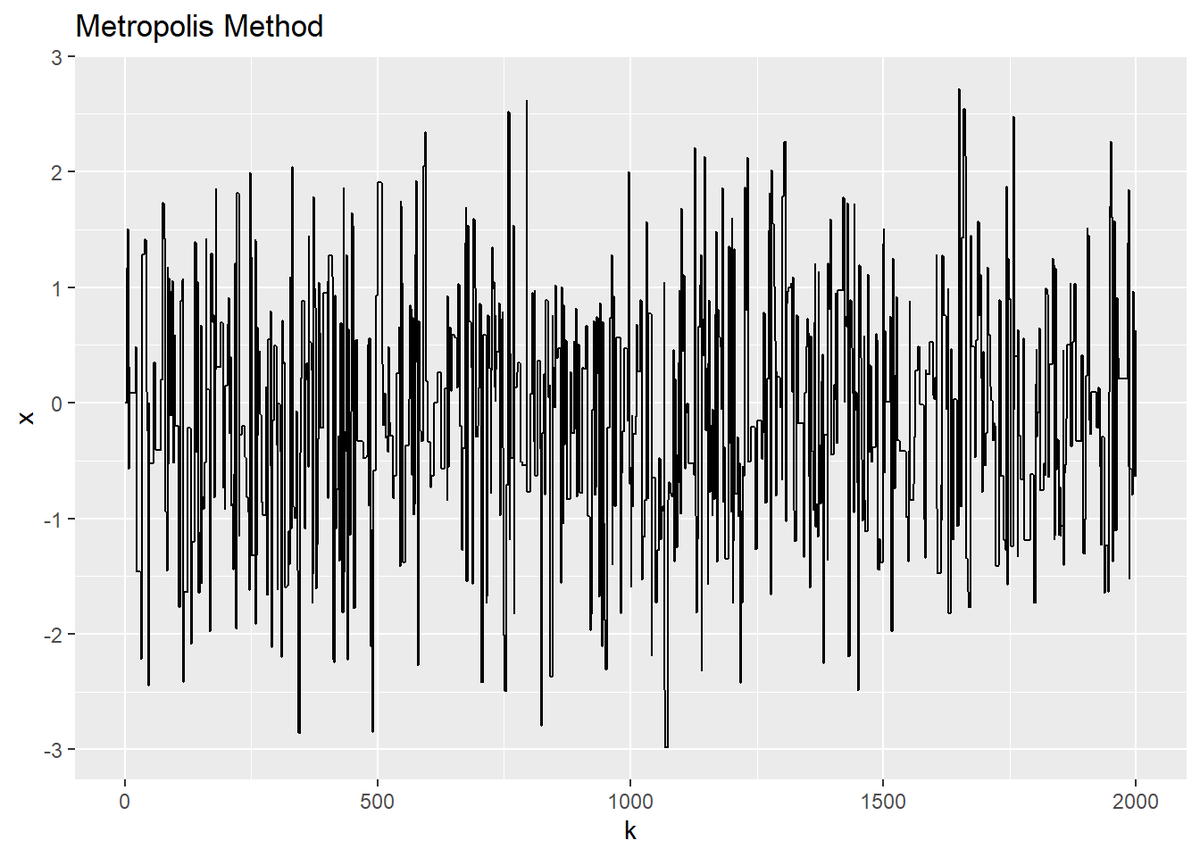
平均値0を中心に、標準偏差の2倍の範囲を行き来しているのが分かります。当然ですが、ヒストグラムで見ても、0付近が一番多く、また左右標準偏差の2倍の間に集中して分布しているのと一致しています。
最後に、$x^{(1)}, \cdots, x^{(K)}$から、$x$の期待値$\mathbb{E}[x] = \mu = 0$と、2乗の期待値$\mathbb{E}[x^2] = \mu^2 + \sigma^2 = 1$をそれぞれ
で近似計算します。
# 期待値を計算 expected_df <- tibble( k = 1:K, x = trace_x, E_x = cumsum(x) / k, E_x2 = cumsum(x^2) / k ) # 期待値の推移をプロット ggplot(expected_df, aes(x = k)) + geom_line(aes(y = E_x), color = "purple") + # xの期待値 geom_hline(aes(yintercept = 0), linetype = "dashed", color = "purple") + # 真のxの期待値 geom_line(aes(y = E_x2), color = "blue") + # x^2の期待値 geom_hline(aes(yintercept = 1), linetype = "dashed", color = "blue") + # 真のx^2の期待値 labs(title = "Metropolis Method", y = "E[f(x)]")
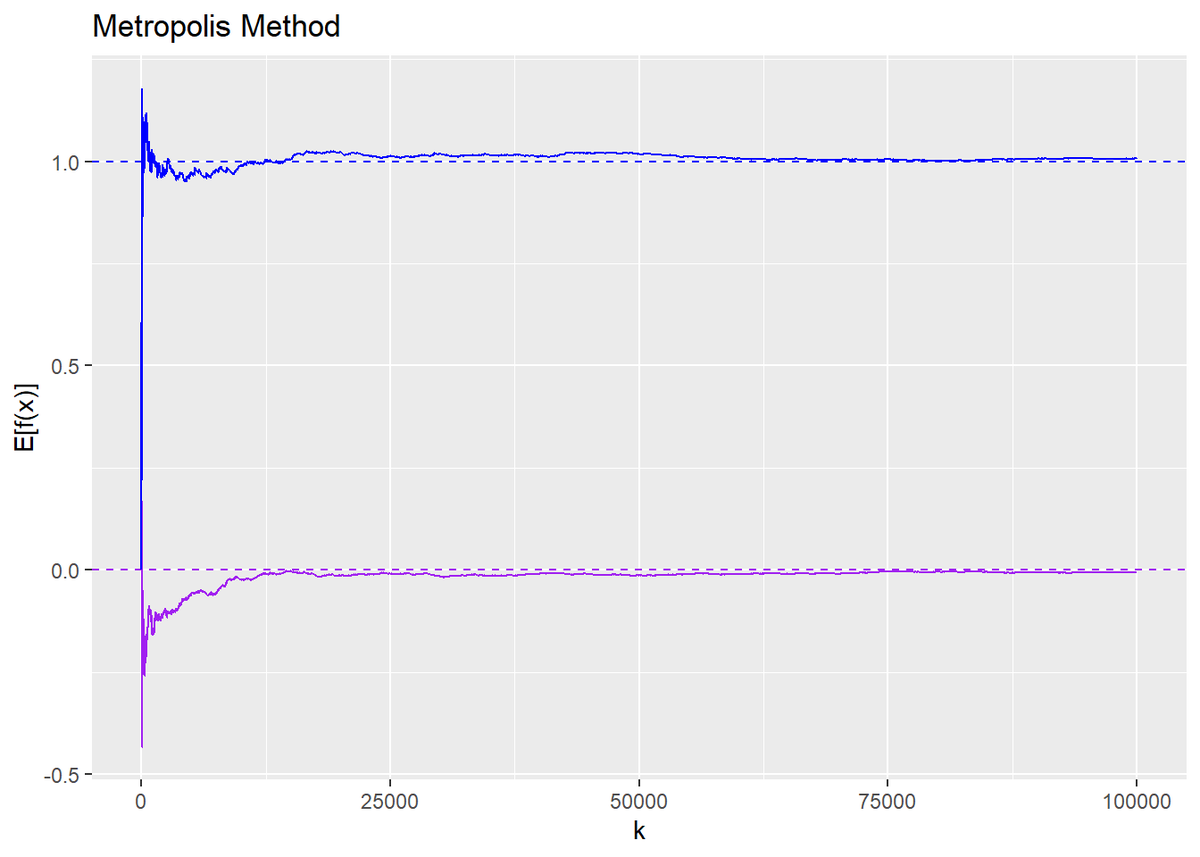
$K$が大きくなるのに従って、それぞれ真の値に近づくのを確認できます。
$K$の変化と分布の変化をアニメーション(gif 画像)で確認するためのコードです。
・コード(クリックで展開)
# 繰り返し回数を指定 K <- 100000 # 一様乱数の範囲(ステップ幅)を指定 c <- 4 # xの初期値を指定 x <- 0 # (重いので)表示する間隔を指定 n_interval <- 50 # フレーム数を計算:(割り切れるように要設定) n_frame <- K / n_interval n_frame # Main loop trace_x <- rep(0, n_frame) anime_df <- tibble() for(k in 1:K) { # xの更新候補を計算 dash_x <- x + runif(n = 1, min = -c, max = c) # テスト値を生成 r <- runif(n = 1, min = 0, max = 1) # メトロポリステストによりxを更新 if(r < exp((0.5 * x^2) - (0.5 * dash_x^2))) { x <- dash_x } # 更新値を記録 trace_x[k] <- x # 結果を記録 if(k %% n_interval == 0) { # k番目までの更新値を格納 tmp_df <- tibble( k = k, x = trace_x ) # 更新結果を結合 anime_df <- rbind(anime_df, tmp_df) # 途中経過を表示 print(paste0(k, " (", round(k / K * 100, 1), "%)")) } } # アニメーション用のヒストグラムを作図 hist_anime <- ggplot() + geom_histogram(data = anime_df, aes(x = x, y = ..density..), binwidth = 0.05, fill = "purple", color = "purple") + # ヒストグラム geom_line(data = true_df, aes(x = x, y = P_x), linetype = "dashed", color = "red") + # 真の確率密度 gganimate::transition_manual(k) + # フレーム ylim(c(0, 1)) + # y軸の範囲 labs(title = "Metropolis Method", subtitle = "k={current_frame}", x = "x", y = "P(x)") # gif画像を作成 gganimate::animate(hist_anime, nframes = n_frame, fps = 25)
更新回数$k$ごとにgif画像のフレームを切り替えます。なので、フレームごとにそれまでの結果のヒストグラムを作図するためのデータフレームを用意する必要があります。処理が重くなるため、作図する間隔をn_intervalとして、n_interval回ごとにそれまでの結果をデータフレームに格納していきます。つまり、10回更新する($K = 10$)場合、anime_dfは$10 + 9 + \cdots + 2 + 1$行のデータフレームになります。
この節では、初期値$x^{(0)}$を適切に決められる場合でした。次節では、初期値がよくない場合を考えます。
4.3 自己相関
4.3.1 初期値との相関とシミュレーションの熱化
初期値と結果との関係を見ます。
その前に、メトロポリス法のコードを汎用的に利用できるように、確率分布$P(x)$と作用$S(x)$の計算を行う関数を作っておくことにします。この関数定義を書き換えることで、利用する確率分布を簡単に切り替えることができます。
# 確率分布を指定 fn_P <- function(x) { exp(-x^2 / 2) / sqrt(2 * pi) #dnorm(x = x, mean = 0, sd = 1) } # 一様分布の範囲(ステップ幅)を指定 c <- 4 # 真の分布を計算 true_df <- tibble( x = seq(-c, c, 0.01), P_x = fn_P(x) ) # 真の分布をプロット ggplot(true_df, aes(x = x, y = P_x)) + geom_line()
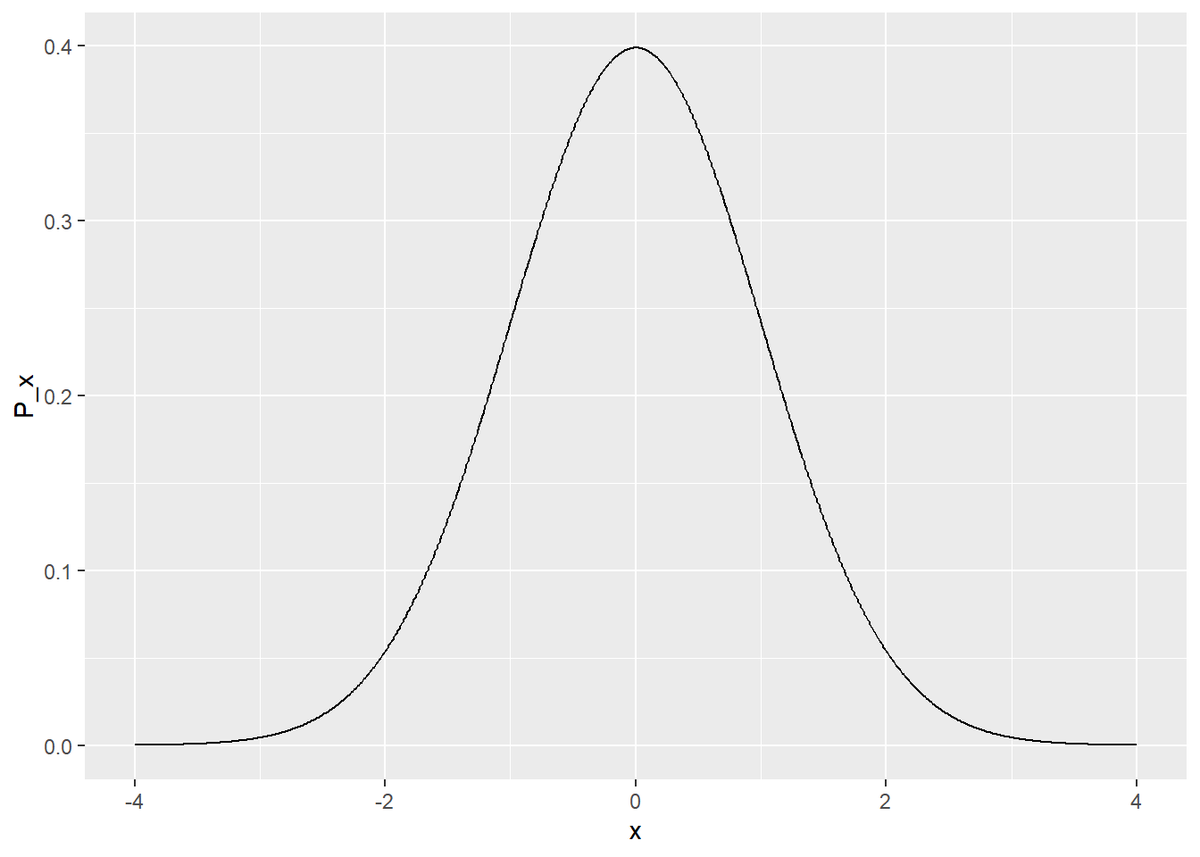
4.3節と同じ分布です。
$P(x)$と$S(x)$を重ねて表示しましょう。
# 作用(負の対数尤度)を指定 fn_S <- function(x) { 0.5 * x^2 } # 確率分布と負の対数尤度をプロット tibble( x = seq(-c, c, 0.01), P_x = fn_P(x), S_x = fn_S(x) ) %>% ggplot(aes(x)) + geom_line(aes(y = P_x)) + geom_line(aes(y = S_x), linetype = "dashed") + labs(y = "f(x)")
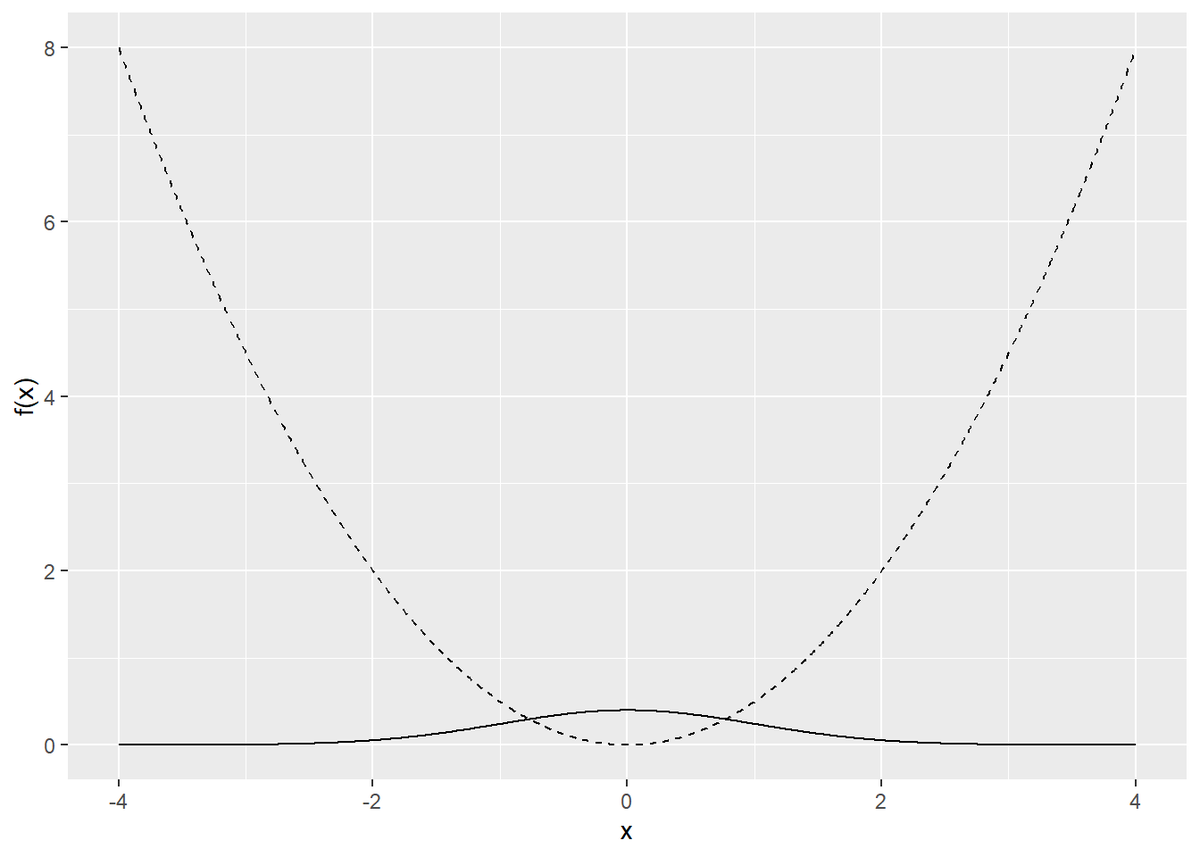
では、初期値を$x^{(0)} = 20$としてメトロポリス法を実行します。
# 繰り返し回数を指定 K <- 100000 # 初期値を指定 x <- 20 # Main loop trace_x <- rep(0, K) for(k in 1:K) { # xの更新候補を計算 dash_x <- x + runif(n = 1, min = -c, max = c) # テスト値を生成 r <- runif(n = 1, min = 0, max = 1) # メトロポリステストによりxを更新 if(r < exp(fn_S(x) - fn_S(dash_x))) { x <- dash_x } # 更新値を記録 trace_x[k] <- x } # 更新値のデータフレームを作成 update_df <- tibble( k = 1:K, x = trace_x ) # 確認 head(update_df)
## # A tibble: 6 x 2 ## k x ## <int> <dbl> ## 1 1 17.7 ## 2 2 17.7 ## 3 3 17.7 ## 4 4 17.7 ## 5 5 17.7 ## 6 6 17.0
メトロポリステストの際に、定義したfn_S()を使って計算しています。
ヒストグラムを見ましょう。コードはさっきと同じです。
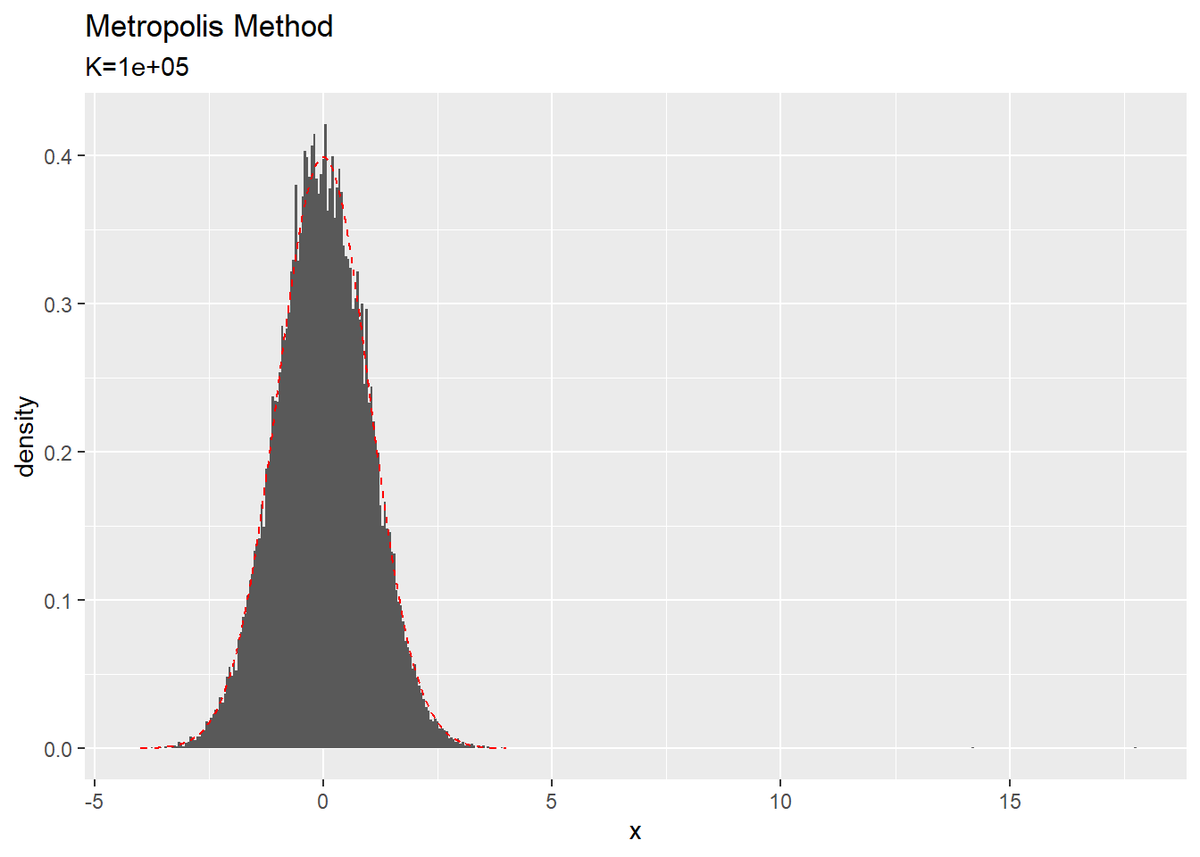
右にポツポツと微かにあるバーが初期値に依存した状態でサンプリングされたものです。また真の分布との近似が悪くなっているのも分かります。
$x^{(k)}$の推移も見ましょう。
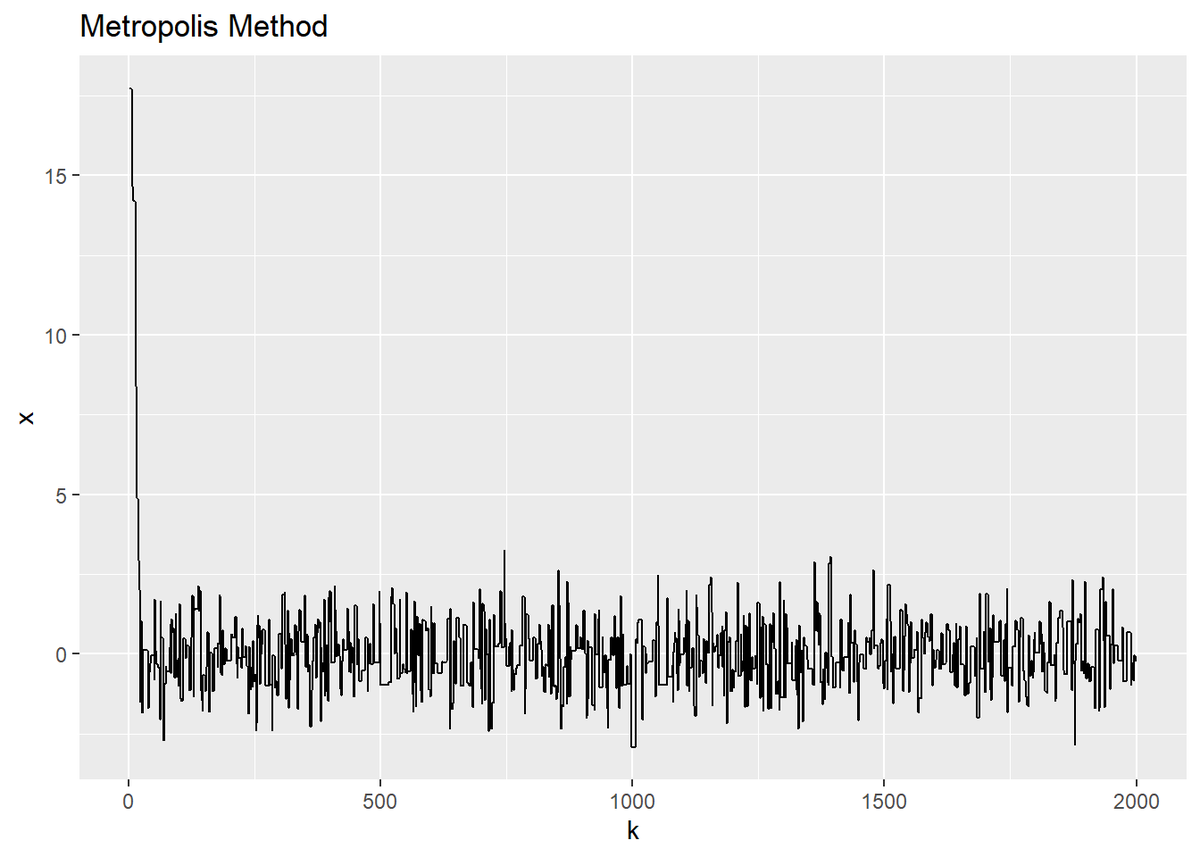
始めの頃は、初期値の影響を受けているのが分かります。
最後に、$x$期待値の近似計算に与える影響を見ます。
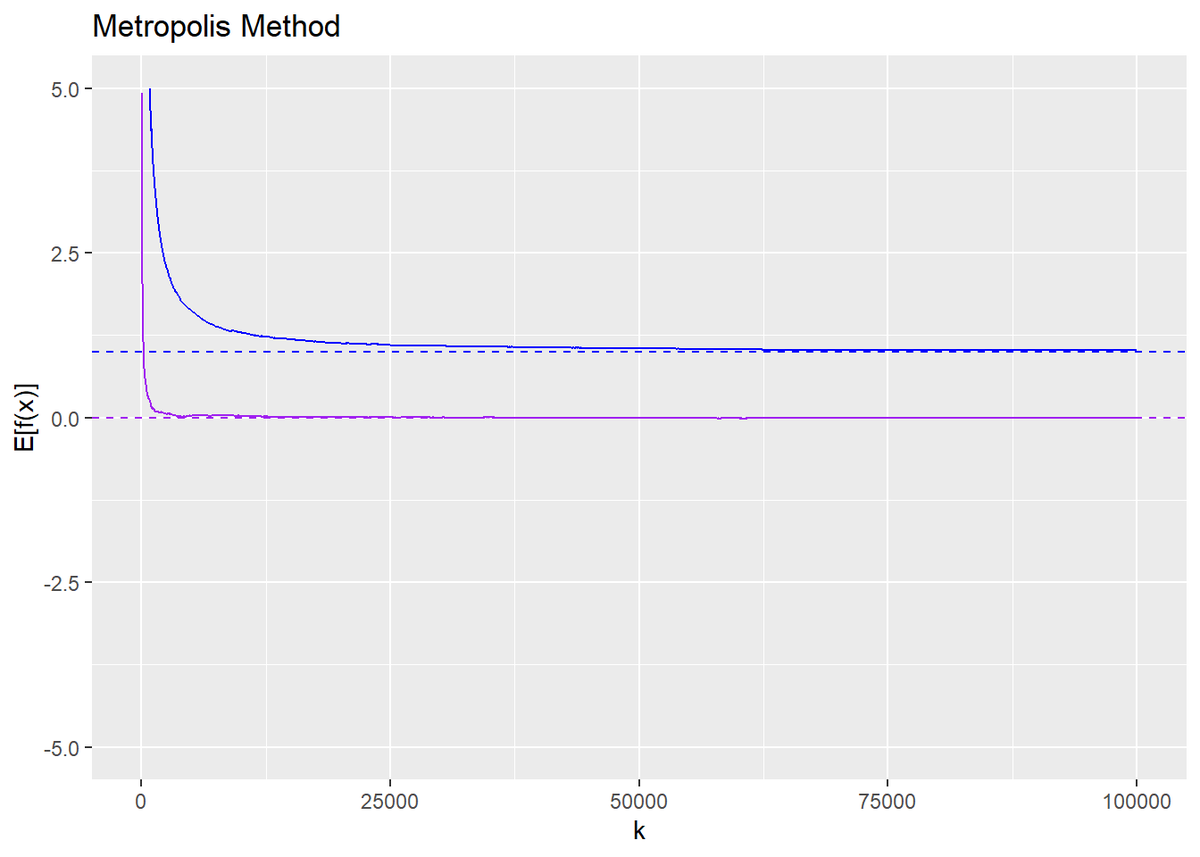
近似できるのに時間がかかっている、あるいは近似できていません。初期値の影響を受けている期間のサンプルを破棄することで上手く近似できると考えられます。
gif作成用のコードも同様に変更します。
・コード(クリックで展開)
# 繰り返し回数を指定 K <- 100000 # 一様分布の範囲(ステップ幅)を指定 c <- 4 # 初期値を指定 x <- 10 # アニメーション表示間隔を指定 n_interval <- 50 # フレーム数を計算:(割り切れるように設定) n_frame <- K / n_interval n_frame # Main loop trace_x <- rep(0, K) anime_df <- tibble() for(k in 1:K) { # xの更新候補を計算 dash_x <- x + runif(n = 1, min = -c, max = c) # テスト値を生成 r <- runif(n = 1, min = 0, max = 1) # メトロポリステストによりxを更新 if(r < exp(fn_S(x) - fn_S(dash_x))) { x <- dash_x } # 更新値を記録 trace_x[k] <- x if(k %% n_interval == 0) { # k番目までの更新値を格納 tmp_df <- tibble( k = k, x = trace_x ) # 結合 anime_df <- rbind(anime_df, tmp_df) # 途中経過を表示 print(paste0(k, " (", round(k / K * 100, 1), "%)")) } } # アニメーション用のヒストグラムを作図 anime_graph <- ggplot() + geom_histogram(data = anime_df, aes(x = x, y = ..density..), binwidth = 0.05, fill = "purple", color = "purple") + # xのヒストグラム geom_line(data = true_df, aes(x = x, y = P_x), linetype = "dashed", color = "red") + # 真の確率密度 ylim(c(0, 1)) + # y軸の表示範囲 gganimate::transition_manual(k) + # フレーム labs(title = "Metropolis Method", subtitle = "k={current_frame}") # gif画像を作成 gganimate::animate(anime_graph, nframes = n_frame, fps = 25)
ここまでは、単純なガウス分布を使用しました。次節では、複雑な分布を使用します。
4.4 ガウス分布以外の例
・混合ガウス分布
2つのガウス分布を合わせた混合ガウス分布
に対して、メトロポリス法を用いましょう。
式(4.14)の計算を行う関数を定義します。
# 確率分布を指定 fn_P <- function(x) { (exp(-0.5 * (x - 3)^2) + exp(-0.5 * (x + 3)^2)) * 0.5 / sqrt(2 * pi) } # 一様分布の範囲(ステップ幅)を指定 c <- 7 # 真の分布を計算 true_df <- tibble( x = seq(-c, c, 0.01), P_x = fn_P(x) ) # 真の分布をプロット ggplot(true_df, aes(x = x, y = P_x)) + geom_line()
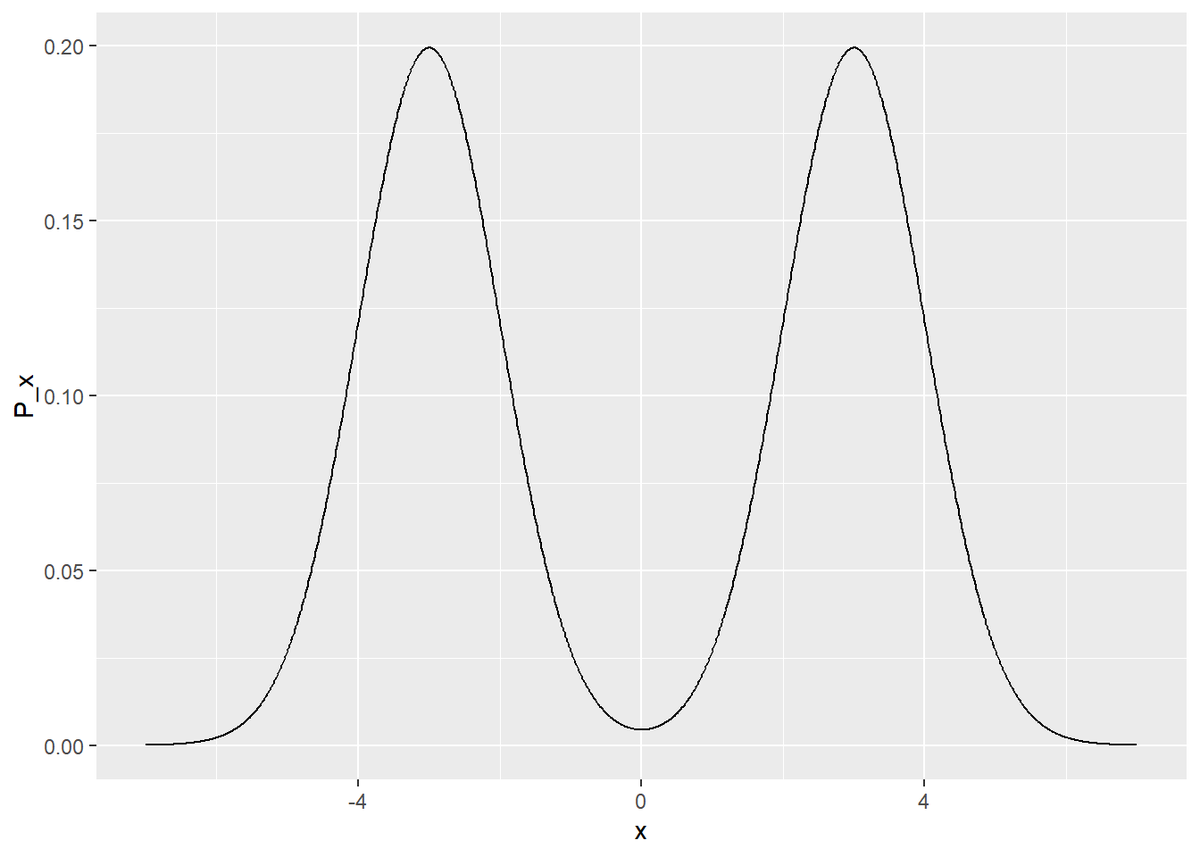
この分布の作用
も作成します。
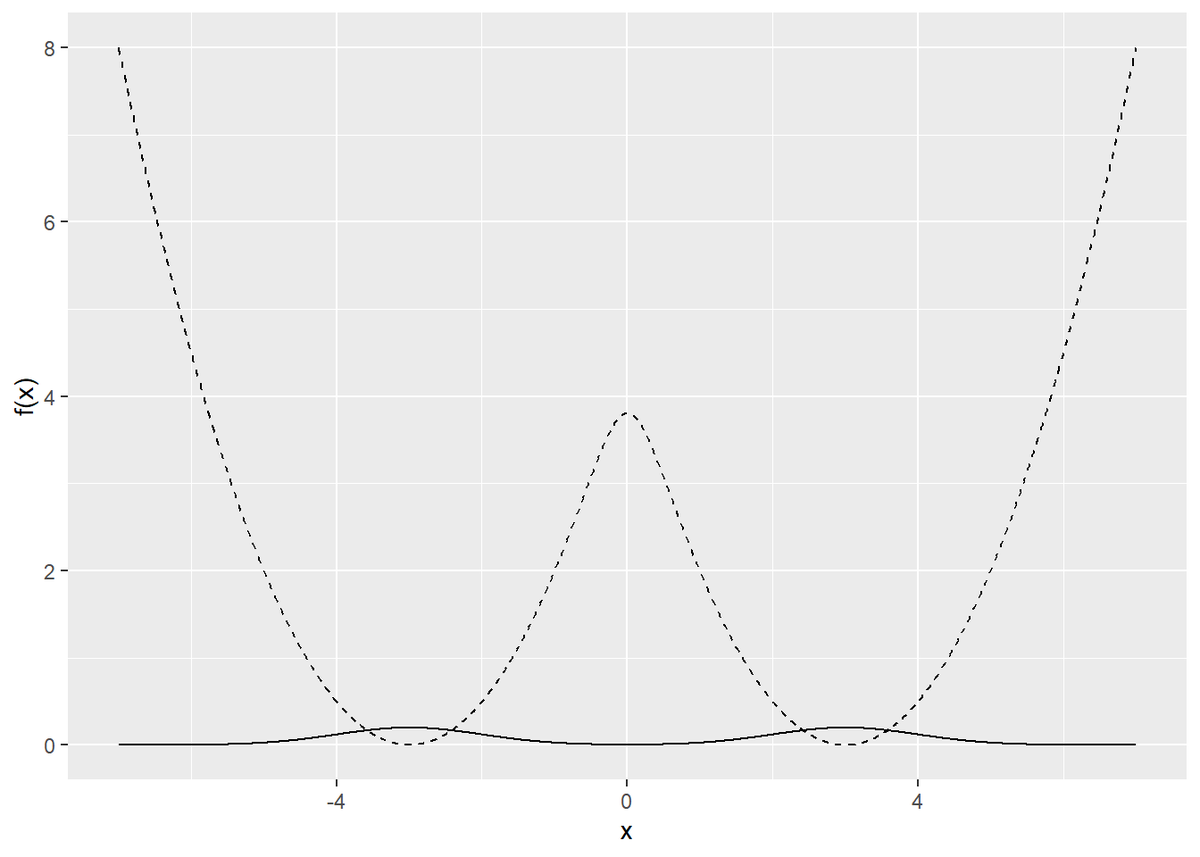
# 作用(負の対数尤度)を指定 fn_S <- function(x) { -log(exp(-0.5 * (x - 3)^2) + exp(-0.5 * (x + 3)^2)) } # 確率分布と負の対数尤度をプロット tibble( x = seq(-c, c, 0.01), P_x = fn_P(x), S_x = fn_S(x) ) %>% ggplot(aes(x)) + geom_line(aes(y = P_x)) + geom_line(aes(y = S_x), linetype = "dashed") + labs(y = "f(x)")
前節のメトロポリス法のコードのままで実行できます。$K = 10000$、初期値$x^{(0)} = 0$とします。
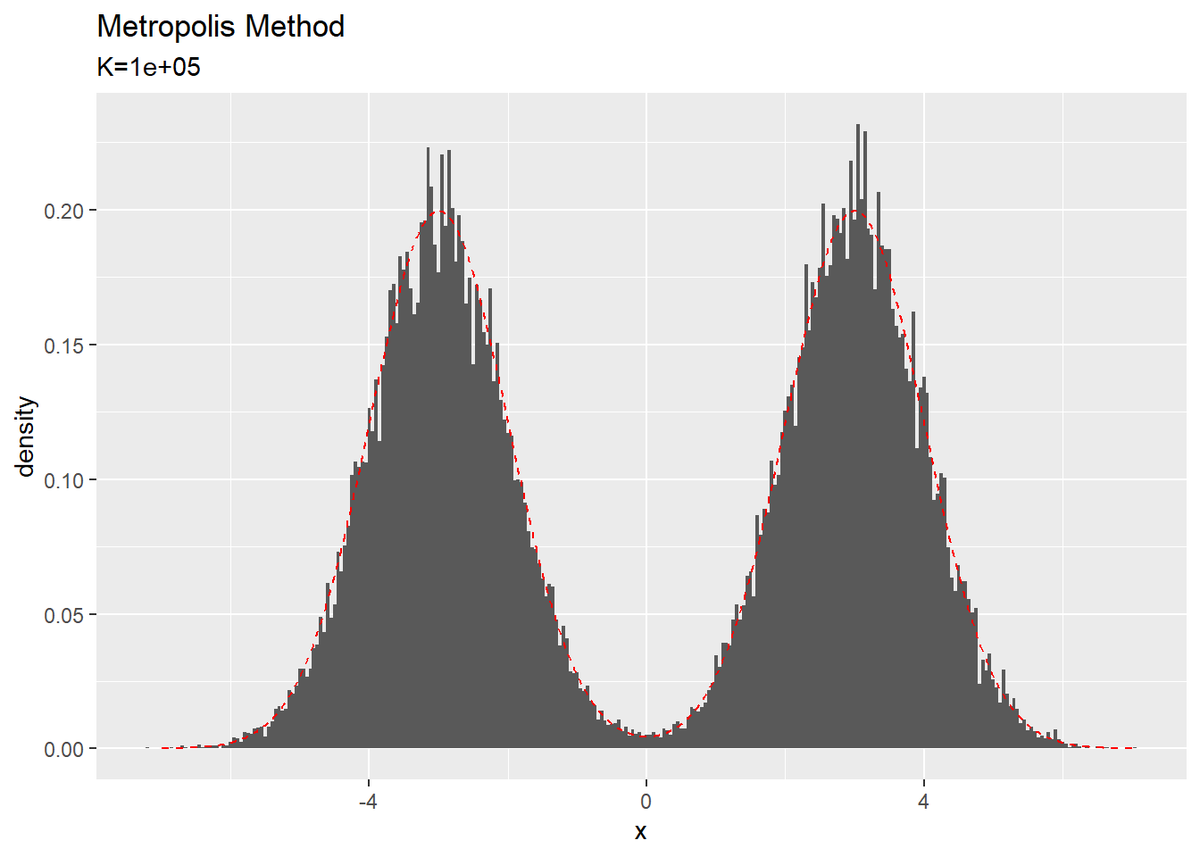
2つのガウス分布を組み合わせた分布に対しても近似できました。$c$の設定を変えて試してみましょう($x$も変えたけど影響が薄かった)。
上に比べて下は、ステップ幅を小さくしたことで2つの山を行き来しにくくなっている(片方の山に留まっている期間が長い)のが分かります。(ylim()の影響でx軸の0の所のバーがおかしな挙動をしています。)
・混合分布
続いて、$x$の値によって確率密度の計算式が変わる確率分布
に対して行います。(混合分布って呼び方でいいのかしら?あとこれって積分して1になるのかな?)
# 確率分布を指定 fn_P <- function(x) { # データ数を取得 n <- length(x) # 受け皿を初期化 P_x <- rep(0, n) # 確率密度を計算 for(i in 1:n) { x_i <- x[i] if(x_i >= 0) { P_x_i <- exp(-0.5 * x_i^2) / sqrt(2 * pi)#dnorm(x = x_i, mean = 0, sd = 1) } else if(x_i >= -1) { P_x_i <- 2 / pi * sqrt(1 - x_i^2) } else if(x_i < -1) { P_x_i <- 0 } P_x[i] <- P_x_i } # 出力 P_x } # 一様分布の範囲(ステップ幅)を指定 c <- 3 # 真の分布を計算 true_df <- tibble( x = seq(-c, c, 0.01), P_x = fn_P(x) ) # 真の分布をプロット ggplot(true_df, aes(x = x, y = P_x)) + geom_line()
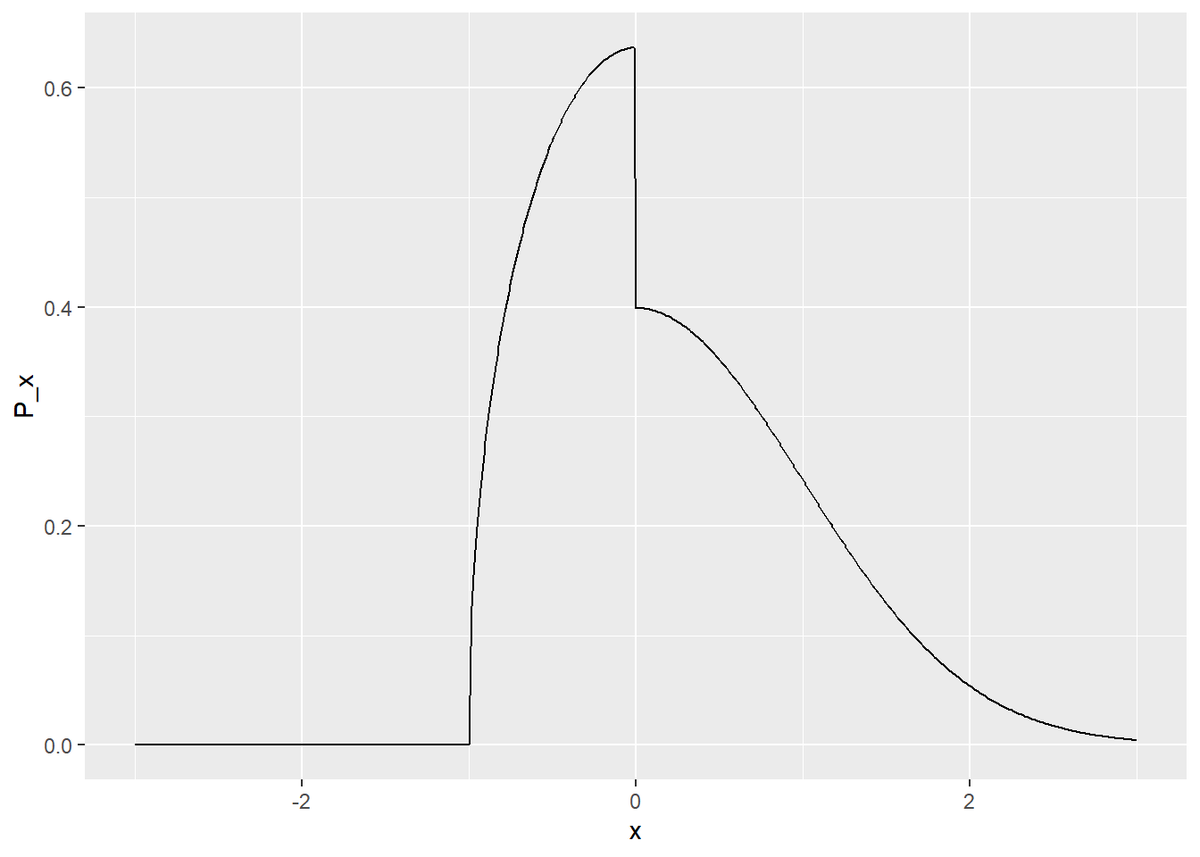
この分布の作用は
となります。自然対数の性質$\log \frac{A}{B} = \log A - \log B$から、1つ目の式は
と整理しています。(この例だと、正規化項も作用に含めないとうまくいかなかった。)
# 作用(負の対数尤度)を指定 fn_S <- function(x) { # データ数を取得 n <- length(x) # 受け皿を初期化 S_x <- rep(0, n) # 確率密度を計算 for(i in 1:n) { x_i <- x[i] if(x_i >= 0) { S_x_i <- 0.5 * x_i^2 + log(sqrt(2 * pi)) } else if(x_i >= -1) { S_x_i <- -log(2 / pi * sqrt(1 - x_i^2)) } else if(x_i < -1) { S_x_i <- -log(0) } S_x[i] <- S_x_i } # 出力 S_x } # 確率分布と負の対数尤度をプロット tibble( x = seq(-c, c, 0.01), P_x = fn_P(x), S_x = fn_S(x) ) %>% ggplot(aes(x)) + geom_line(aes(y = P_x)) + geom_line(aes(y = S_x), linetype = "dashed") + labs(y = "f(x)")
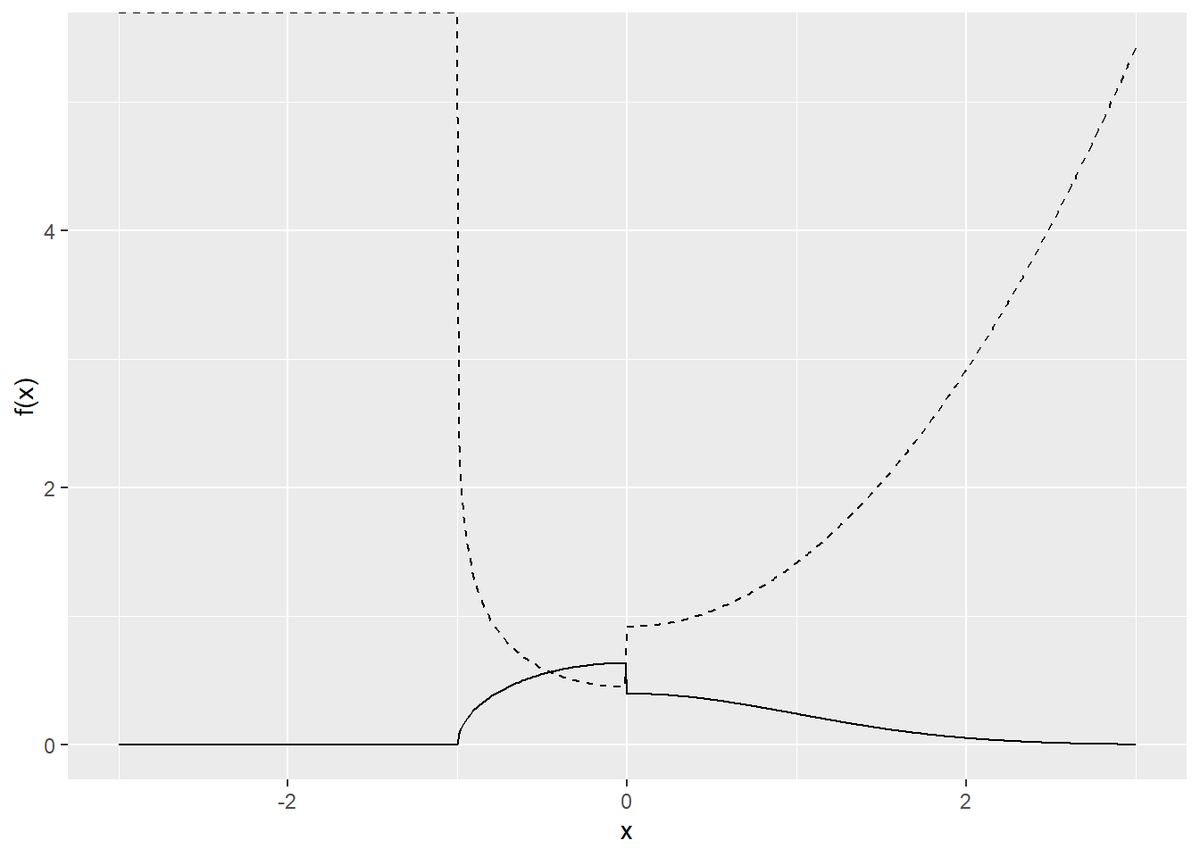
(ところで、for()を使わずに要素ごとに条件分岐して別の計算するのを実装できなかった…)
では、この分布も初期値を0としてメトロポリス法により近似します。

複雑な分布に対しても近似できました。
4章では、1つの変数(1次元)の分布を扱いました。次章では、2つの変数(2次元)の分布に対してメトロポリス法を行います。
参考文献
- 花田政範・松浦壮『ゼロからできるMCMC』講談社,2020年.
おわりに
ジャックナイフ法がよく分からなかった。調べて出てくるのはサンプリングするとかでなんか違った。新しく登場する記号はもう少し説明してほしいです、、、4.5節についても同様にパスです。
【次の章の内容】