4.3：改良版word2vecの学習【ゼロつく2のノート(実装)】

はじめに

　『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。

　本の内容を1つずつ確認しながらゆっくりと組んでいきます。

　この記事は、4.3節「改良版word2vecの学習」の内容です。改良版のCBOWモデルをPythonで実装して、PTBデータセットを用いて学習を行います。

【前節の内容】

www.anarchive-beta.com

【他の節の内容】

www.anarchive-beta.com

【この節の内容】

4.3.1 CBOWモデルの実装

　これまで実装したレイヤを用いて効率よく処理を行うCBOWモデルを実装します。

　この項では、これまでに実装した関数preprocess()(2.3.1項)とcreate_contexts_target()(3.3.1項)を利用します。そのため関数定義を再実行するか、次の方法で読み込む必要があります。

# 読み込み用の設定
import sys
sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master')

# 実装済みの関数をインポート
from common.util import preprocess
from common.util import create_contexts_target

# 利用するライブラリ
import numpy as np

・処理の確認

　まずは3章で行ったテキストの前処理を行います。

# テキストを設定
text = 'You say goodbye and I say hello.'

# 単語と単語IDに変換
corpus, word_to_id, id_to_word = preprocess(text)
print(corpus)

# 語彙数(単語の種類数)を取得
vocab_size = len(word_to_id)

# ウィンドウサイズを指定
window_size = 1

# コンテキストとターゲットを作成
contexts, target = create_contexts_target(corpus, window_size=window_size)
print(target)
print(contexts)

[0, 1, 2, 3, 4, 1, 5, 6]
[1 2 3 4 1 5]
[[0 2]
 [1 3]
 [2 4]
 [3 1]
 [4 5]
 [1 6]]

　ウィンドウサイズはターゲットの前後何語をコンテキストとするかを表す範囲でした。つまりウィンドウサイズの2倍の値がコンテキストの単語数になります。このコンテキストの単語ごとに入力層(Embeddingレイヤ)が必要になります。
　必要な数のEmbeddingレイヤ(4.1.2項)のインスタンスをfor文で作成して、リストin_layersに格納します。

# 中間層のニューロン数を指定
hidden_size = 3

# 入力層の重みを初期化
W_in = 0.01 * np.random.randn(vocab_size, hidden_size)

# 入力層のインスタンスを作成
in_layers = []
for i in range(2 * window_size):
    layer = Embedding(W_in)
    in_layers.append(layer)

　出力層と損失層を合わせたNegative Sampling Lossレイヤ(4.2.7項)のインスタンスを作成します。

# 出力層の重みを初期化
W_out = 0.01 * np.random.randn(vocab_size, hidden_size)

# 出力層のインスタンスを作成
ns_loss_layer = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)

　入力層と出力層(全てのレイヤ)のインスタンスを1つのリストにまとめておきます。

　また各レイヤのインスタンスが保持している重みと勾配もそれぞれリストにまとめておきます。

# レイヤをまとめる
layers = in_layers + [ns_loss_layer]

# 重みと勾配をまとめる
params = [] # 重み
grads = []  # 勾配
for layer in layers:
    params += layer.params
    grads += layer.grads

　リストに格納されているレイヤのクラスは、type()で確認できます。

# 格納されているレイヤを確認
for layer in layers:
    print(type(layer))

<class '__main__.Embedding'>
<class '__main__.Embedding'>
<class '__main__.NegativeSamplingLoss'>

　この例ではウィンドウサイズを1としたので、Embeddingレイヤのインスタンスが2つ格納されています。

　レイヤの準備が整ったので、順伝播の処理を行い損失を計算します。

　全ての入力層の計算結果の平均が出力層に伝播します(図3-11)。

# 中間層のニューロンを計算
h = 0 # 初期化
for i, layer in enumerate(in_layers):
    h += layer.forward(contexts[:, i])
    h *= 1 / len(in_layers)

# 損失を計算
loss = ns_loss_layer.forward(h, target)
print(loss)

4.158855591743863

　続いて逆伝播の処理を行い各入力層の重みに関する勾配を計算します。

　順伝播において入力層から出力層に伝播する際に、平均をとる計算をしました。このとき、コンテキストの数(入力層の数)分の1を掛ける計算をしています。よって逆伝播においても、入力層の数で割る(入力層の数分の1を掛ける)必要があります(1.3.4.1項)。

# 逆伝播の入力
dout = 1

# 出力層の勾配を計算
dout = ns_loss_layer.backward(dout)

# 入力層の勾配を計算
dout *= 1 / len(in_layers)
for layer in in_layers:
    layer.backward(dout)
    print(np.round(layer.grads, 3))

[[[ 0.    -0.001 -0.001]
  [-0.004  0.002  0.   ]
  [-0.001  0.001  0.001]
  [-0.001  0.     0.   ]
  [ 0.    -0.001 -0.001]
  [ 0.     0.     0.   ]
  [ 0.     0.     0.   ]]]
[[[ 0.     0.     0.   ]
  [-0.001  0.     0.   ]
  [ 0.    -0.001 -0.001]
  [-0.002  0.001  0.   ]
  [-0.001  0.001  0.001]
  [ 0.    -0.001 -0.001]
  [-0.002  0.001 -0.   ]]]

　入力層ごとに勾配を持ちます。

・実装

　処理の確認ができたので、CBOWモデルをクラスとして実装します。

# 改良版CBOWの実装
class CBOW:
    # 初期化メソッドの定義
    def __init__(self, vocab_size, hidden_size, window_size, corpus):
        V, H = vocab_size, hidden_size
        
        # 重みを初期化
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(V, H).astype('f')
        
        # 入力層を作成
        self.in_layers = []
        for i in range(2 * window_size):
            layer = Embedding(W_in)
            self.in_layers.append(layer)
        
        # 出力・損失層を作成
        self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)
        
        # レイヤをまとめる
        layers = self.in_layers + [self.ns_loss]
        
        # 重みと勾配をまとめる
        self.params = [] # 重み
        self.grads = []  # 勾配
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads
        
        # 分散表現を保存
        self.word_vecs = W_in
    
    # 順伝播メソッドの定義
    def forward(self, contexts, target):
        # 中間層のニューロンを計算
        h = 0
        for i, layer in enumerate(self.in_layers):
            h += layer.forward(contexts[:, i])
        h *= 1 / len(self.in_layers)
        
        # 損失を計算
        loss = self.ns_loss.forward(h, target)
        return loss
    
    # 逆伝播メソッドの定義
    def backward(self, dout=1):
        # 出力層の勾配を計算
        dout = self.ns_loss.backward(dout)
        
        # 入力層の勾配を計算
        dout *= 1 / len(self.in_layers)
        for layer in self.in_layers:
            layer.backward(dout)
        
        return None

　CBOWモデルのインスタンスを作成して、順伝播メソッドを実行します。

# CBOWのインスタンスを作成
model = CBOW(vocab_size, hidden_size, window_size, corpus)

# 順伝播の処理
loss = model.forward(contexts, target)
print(loss)

4.15881363550822

　損失が出力されました。

　続いて逆伝播メソッドを実行します。

# 逆伝播の処理
model.backward()

# 結果を確認
for grad in model.grads:
    print(np.round(grad, 3))

・省略(クリックで展開)

[[-0.    -0.002  0.002]
 [ 0.001 -0.002  0.002]
 [ 0.001  0.     0.001]
 [ 0.     0.001  0.002]
 [ 0.    -0.002  0.001]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]]
[[ 0.     0.     0.   ]
 [ 0.     0.001  0.002]
 [-0.    -0.002  0.002]
 [ 0.001 -0.001 -0.001]
 [ 0.001  0.     0.001]
 [ 0.    -0.002  0.001]
 [ 0.    -0.001  0.002]]
[[ 0.     0.     0.   ]
 [ 0.    -0.001  0.002]
 [-0.     0.001 -0.   ]
 [-0.    -0.     0.001]
 [-0.     0.001 -0.   ]
 [-0.     0.    -0.   ]
 [ 0.     0.     0.   ]]
[[ 0.    -0.001  0.   ]
 [ 0.    -0.001  0.   ]
 [ 0.    -0.     0.   ]
 [ 0.     0.     0.   ]
 [ 0.     0.    -0.001]
 [-0.     0.001 -0.002]
 [ 0.     0.     0.   ]]
[[ 0.    -0.    -0.002]
 [ 0.001  0.    -0.001]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]
 [ 0.    -0.001  0.   ]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]]
[[ 0.001  0.    -0.001]
 [ 0.     0.     0.   ]
 [ 0.    -0.001  0.   ]
 [ 0.    -0.001  0.   ]
 [ 0.     0.     0.   ]
 [ 0.     0.     0.   ]
 [-0.     0.001 -0.002]]
[[ 0.     0.     0.   ]
 [ 0.     0.     0.   ]
 [-0.     0.001 -0.003]
 [ 0.     0.    -0.001]
 [ 0.    -0.     0.   ]
 [ 0.    -0.001  0.   ]
 [ 0.    -0.001  0.   ]]
[[ 0.     0.     0.   ]
 [ 0.     0.     0.   ]
 [ 0.     0.    -0.001]
 [ 0.    -0.     0.   ]
 [-0.     0.    -0.001]
 [ 0.    -0.001  0.   ]
 [ 0.001 -0.    -0.001]]

　勾配の数は、入力層の数(コンテキストの単語数=ウィンドウサイズの2倍)、出力層の正例(1)、出力層の負例のサンプルサイズ(実装時に指定した5)の合計になります。

　最後に単語の分散表現を出力します。

# 単語の分散表現を確認
print(model.word_vecs)

[[ 0.00133948  0.00092787 -0.00568738]
 [ 0.00659573 -0.01095479  0.01300096]
 [ 0.00233152  0.0050649  -0.01953738]
 [ 0.00174303 -0.00476704 -0.01157386]
 [ 0.00156722  0.002556   -0.01181583]
 [-0.0101499   0.00479364 -0.01834535]
 [ 0.00229933  0.00421572 -0.0035261 ]]

　各行が各語彙に対応しているのでした。この例では各単語を3次元(中間層のニューロン数)のベクトルで表現するように学習を行っています。

　以上で処理を効率化したCBOWモデルを実装できました！次項では、このモデルとPTBコーパスを用いて学習を行います。

4.3.2 CBOWモデルの学習コード

　前項で実装したCBOWモデルとPTBデータセットを用いて学習を行います。PTBデータセットについては2.4.4項でも利用しました。

　この項では、3.3.1項で実装したコーパスからターゲットとコンテキストを抽出する関数create_contexts_target()と、1.4.4項で実装した学習処理用のクラスTrainerを利用します。そぞれの定義を再実行するか、次の方法で実装済みのものを読み込む必要があります。

# 読み込み用の設定
import sys
sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master')

# 実装済みの関数をインポート
from dataset import ptb
#from common.util import create_contexts_target
#from common.trainer import Trainer
from common.optimizer import Adam

# 利用するライブラリ
import numpy as np
import matplotlib.pyplot as plt

　まずはハイパーパラメータを設定します。

# ウィンドウサイズ
window_size = 5

# 中間層のニューロン数
hidden_size = 100

# バッチデータ数
batch_size = 100

# 試行回数
max_epoch = 10

　テキストデータ(コーパス)を読み込んで前処理を行います(2.3.4項)。

# データを読み込む
corpus, word_to_id, id_to_word = ptb.load_data('train')
print(corpus.shape)

# 語彙数を取得
vocab_size = len(word_to_id)
print(vocab_size)

# コンテキストとターゲットを抽出する
contexts, target = create_contexts_target(corpus, window_size)
print(contexts.shape)
print(target.shape)

(929589,)
10000
(929579, 10)
(929579,)

　contextsの列数は、window_sizeの2倍になるのでした。

　各種インスタンスを作成します。

# モデルのインスタンスを作成
model = CBOW(vocab_size, hidden_size, window_size, corpus)

# 最適化手法のインスタンスを作成
optimizer = Adam()

# 学習用クラスのインスタンスを作成
trainer = Trainer(model, optimizer)

　Trainerクラスのfit()メソッドによって学習を行います。

# 学習
trainer.fit(contexts, target, max_epoch, batch_size)

| epoch 1 | iter 20 / 9295 | time 1[s] | loss 4.16
| epoch 1 | iter 40 / 9295 | time 2[s] | loss 4.15
| epoch 1 | iter 60 / 9295 | time 4[s] | loss 4.13
(省略)
| epoch 10 | iter 9260 / 9295 | time 6893[s] | loss 1.47
| epoch 10 | iter 9280 / 9295 | time 6895[s] | loss 1.47

　lossの推移を確認しましょう。plot()メソッドでグラフを出力します。

# 推移を確認
trainer.plot()

lossの推移

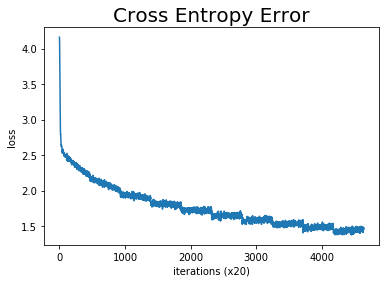
　次項で用いるために学習済みの単語の分散表現を取得します。

# 単語の分散表現を取得
word_vecs = model.word_vecs
print(word_vecs.shape)

(10000, 100)

　vocab_size行hidden_size列の行列が出力されました。各行が各語彙の単語ベクトルに対応しています。

　以上で学習を行えました！次項では、単語の分散表現を評価します。

4.3.3 CBOWモデルの評価

　CBOWモデルの学習によって得られた単語の分散表現を用いて、モデルの評価をします。
　まずは2.3.5項で行った類似度の高い単語を検索します。次に類推問題を解くための関数を実装します。

　単語ベクトルの類似度を測るのに、2.3.5-6項で実装した関数cos_similarity()とmost_similar()を使います。関数定義を再実行するか以下の方法で読み込みます。

# 実装済みの関数をインポート
from common.util import cos_similarity
from common.util import most_similar

・類似問題

　単語を指定し、各単語とのコサイン類似度が高い単語を出力します。

# 対象とする単語を指定
querys = ['you', 'year', 'car', 'toyota']

# 1語ずつコサイン類似度の高い単語を検索
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

[query] you
 we: 0.7386575937271118
 i: 0.6925641298294067
 your: 0.6210212111473083
 they: 0.6107571125030518
 anybody: 0.5998017191886902

[query] year
 month: 0.8663298487663269
 summer: 0.7875156998634338
 week: 0.7833577394485474
 spring: 0.7631788849830627
 decade: 0.7040307521820068

[query] car
 window: 0.6317394971847534
 luxury: 0.6315163373947144
 truck: 0.6308699250221252
 cars: 0.6225758790969849
 auto: 0.5799184441566467

[query] toyota
 honda: 0.6261252760887146
 nissan: 0.6184272170066833
 mazda: 0.6161534190177917
 seita: 0.6070237159729004
 engines: 0.5912835597991943

　同じカテゴリに属するような単語が上位になっていることから、各単語をベクトルで上手く表現できているといえるでしょう。

・類推問題

　続いて類推問題を解きます。類推問題とは$\mathrm{king} - \mathrm{man} + \mathrm{woman} = \mathrm{query}$のような問題のことで、つまり「男の王」(という概念) から「男」を引き「女」を足すと「女の王」になるということです。この計算をword2vecの単語ベクトルを用いて求めることができることが分かっています。

　まずは単語を指定して、単語の分散表現word_vecsから各単語のベクトルを抽出します。

# 単語を指定
man, king, woman = 'man', 'king', 'woman'

# 単語IDを取得
man_id, king_id, woman_id = word_to_id[man], word_to_id[king], word_to_id[woman]
print(man_id, king_id, woman_id)

# 単語ベクトルを取得
man_vec, king_vec, woman_vec = word_vecs[man_id], word_vecs[king_id], word_vecs[woman_id]
print(man_vec)

2079 7103 2397
[ 8.07224929e-01  9.96359289e-02 -1.15002024e+00  4.34431821e-01
  1.14492512e+00  3.92022729e-01 -6.20227993e-01 -9.61108327e-01
  6.04005754e-01 -4.17391062e-02 -1.17249143e+00  8.64485025e-01
  1.07163274e+00  4.62227583e-01  1.02499045e-01 -8.10952425e-01
  1.96018413e-01  6.29905283e-01 -1.83377326e-01  1.19254529e+00
 -5.53887844e-01  5.63787401e-01  1.26814616e+00 -8.38608146e-01
 -4.54323858e-01  1.15431428e+00  1.43760860e-01  6.31318688e-01
  1.28088221e-01 -1.86529601e+00 -4.23999177e-03  5.83172858e-01
 -8.08478832e-01  1.43853831e+00 -1.22658741e+00  1.42141855e+00
 -1.59885836e+00 -1.26853955e+00 -1.84733853e-01  1.01103079e+00
 -2.66343981e-01 -4.13716018e-01  1.49563527e+00  1.97554171e-01
 -4.14673385e-04 -5.11094451e-01 -9.99373436e-01  4.28700417e-01
 -2.51687188e-02 -1.49246752e-01  5.87706327e-01 -5.87987125e-01
 -4.86038685e-01 -8.54517937e-01 -4.97008353e-01 -7.70755053e-01
 -5.07067628e-02  1.33506620e+00  8.46744180e-01 -3.22390437e-01
 -1.36871409e+00  1.04872227e+00  2.02080345e+00  1.03962231e+00
  5.64554930e-01  1.04901052e+00  7.82609805e-02 -5.37388921e-01
  9.30938780e-01  4.19442713e-01 -6.69946790e-01  5.81679344e-01
 -1.63660258e-01  7.73129880e-01 -1.01378727e+00  6.09823227e-01
  3.17693740e-01 -6.27007723e-01  9.39426959e-01  1.04290342e+00
  5.86498559e-01 -1.07246053e+00  2.46321499e-01  9.02571142e-01
  5.08101732e-02 -6.70872808e-01 -1.10096145e+00 -1.85683858e+00
 -8.01580429e-01  4.67679799e-02 -1.46497202e+00  2.06840396e+00
  4.73787993e-01  4.44362551e-01 -9.60365117e-01 -1.26562762e+00
  1.80228025e-01 -4.02877897e-01  2.07294434e-01  1.61894679e-01]

　$\mathrm{king} - \mathrm{man} + \mathrm{woman} = \mathrm{query}$の式に従い、単語ベクトル間の計算を行います。

　更に、コサイン類似度の計算(2.3.5項)にて行う

$$ \left( \frac{x_1}{\sqrt{\sum_{i=1}^n x_i}}, \frac{x_2}{\sqrt{\sum_{i=1}^n x_i}}, \cdots, \frac{x_n}{\sqrt{\sum_{i=1}^n x_i}} \right) \tag{2.1'} $$

の計算によって、求めたクエリの単語ベクトルを正規化します。この式の分母である2乗和の平方根をノルム$|\mathbf{x}|$と呼ぶのでした。

# 求めたい単語のベクトルを計算
query_vec = king_vec - man_vec + woman_vec
print(np.round(query_vec, 2))

# ノルム(2乗和の平方根)を計算
s = np.sqrt((query_vec * query_vec).sum())

# 正規化
query_vec /= s
print(np.round(query_vec, 2))

[-0.2  -0.66 -0.83  0.48  0.44  0.09 -0.84 -0.73 -0.32 -0.4   1.27  0.22
  0.26  0.56  0.33  0.12 -1.34 -0.3  -0.28  0.21  0.38  1.48 -0.18 -0.2
  0.63  1.94  0.33  1.06 -0.46  1.67  1.67 -0.21  0.59 -0.73 -1.38  0.7
 -0.34 -1.15 -0.34  0.12  0.39  0.66 -0.39  0.67  1.71  1.59  1.01  0.35
 -0.49 -0.23 -0.37 -0.24 -0.67 -0.62  0.37 -0.29  0.93  0.22  0.1   1.3
 -1.11 -0.19  0.21  1.32  0.53  0.72 -0.96 -0.42 -0.17 -0.75  0.16  0.21
  1.1  -1.29  0.81  1.25 -0.29 -0.2   0.49  0.48 -0.45 -1.19 -0.65  1.65
  0.76 -0.86 -0.24 -0.03  0.47 -0.19  0.39  1.36 -0.94 -0.29 -0.8  -0.74
  0.19 -1.16  1.24  0.04]
[-0.03 -0.08 -0.1   0.06  0.06  0.01 -0.11 -0.09 -0.04 -0.05  0.16  0.03
  0.03  0.07  0.04  0.02 -0.17 -0.04 -0.04  0.03  0.05  0.19 -0.02 -0.03
  0.08  0.25  0.04  0.13 -0.06  0.21  0.21 -0.03  0.07 -0.09 -0.18  0.09
 -0.04 -0.15 -0.04  0.02  0.05  0.08 -0.05  0.08  0.22  0.2   0.13  0.04
 -0.06 -0.03 -0.05 -0.03 -0.09 -0.08  0.05 -0.04  0.12  0.03  0.01  0.16
 -0.14 -0.02  0.03  0.17  0.07  0.09 -0.12 -0.05 -0.02 -0.09  0.02  0.03
  0.14 -0.16  0.1   0.16 -0.04 -0.02  0.06  0.06 -0.06 -0.15 -0.08  0.21
  0.1  -0.11 -0.03 -0.    0.06 -0.02  0.05  0.17 -0.12 -0.04 -0.1  -0.09
  0.02 -0.15  0.16  0.  ]

　この2乗和の平方根で割る計算を正規化関数normalize()として定義しておきます。

# コサイン類似度における正規化関数の実装
def normalize(x):
    if x.ndim == 2: # 2次元配列のとき
        # 行ごとにノルムを計算
        s = np.sqrt((x * x).sum(1))
        
        # 正規化:式(2.1')
        x /= s.reshape((s.shape[0], 1))
    elif x.ndim == 1: # 1次元配列のとき
        # 正規化:式(2.1')
        s = np.sqrt((x * x).sum())
        x /= s
    return x

　2次元配列(複数の単語ベクトル)の場合には行(単語ベクトル)ごとに正規化する必要があるため、この実装ではif文で場合分けして次のような処理を行います。

# 2次元配列を作成
X = np.array([[1.0, 2.0, 3.0, 4.0, 5.0], [1.0, 2.0, 3.0, 4.0, 5.0], [1.0, 2.0, 3.0, 4.0, 5.0]])
print(X)

# 行ごとに和をとる
S = np.sqrt((X * X).sum(1))
print(S)

# 縦ベクトルに変換
S = S.reshape((S.shape[0], 1))
print(S)

# 列ごとに割る
X /= S
print(X)

[[1. 2. 3. 4. 5.]
 [1. 2. 3. 4. 5.]
 [1. 2. 3. 4. 5.]]
[7.41619849 7.41619849 7.41619849]
[[7.41619849]
 [7.41619849]
 [7.41619849]]
[[0.13483997 0.26967994 0.40451992 0.53935989 0.67419986]
 [0.13483997 0.26967994 0.40451992 0.53935989 0.67419986]
 [0.13483997 0.26967994 0.40451992 0.53935989 0.67419986]]

　全ての単語ベクトルword_vecsとクエリの単語ベクトルとの内積を計算します。

# 全ての単語とのコサイン類似度を計算:式(2.1)
similarity = np.dot(word_vecs, query_vec)
print(np.round(similarity, 2))

[0.05 0.11 0.19 ... 1.08 2.38 0.52]

　計算結果の各要素は、各単語とのコサイン類似度です。

　argsort()メソッドは、リストの要素を値が低い順に並べ替えたインデックスを出力します。-1を掛けて符号を反転させることで大小関係を反転っせてからargsort()を使うことで、値が高い順にインデックスを出力できます。

# クエリとの類似度が低い順に単語のインデックスを抽出
similarity_idx_desc = similarity.argsort()
print(similarity_idx_desc)

# クエリとの類似度が高い順に単語のインデックスを抽出
similarity_idx_asc = (-1 * similarity).argsort()
print(similarity_idx_asc)

[5788  596 1404 ... 7546 7103 2397]
[2397 7103 7546 ... 1404  596 5788]

　処理結果の各要素は、単語IDに対応します。

　リストの要素を順番に取り出して、対応する単語と類似度の値を表示します。指定した単語数まで繰り返し行います。

# 表示する上位単語数を指定
top = 10

# クエリとの類似度の高い単語を表示
count = 0 # カウントを初期化
for word_id in similarity_idx_asc:
    # 単語を取得
    top_word = id_to_word[word_id]
    
    # クエリとの類似度を取得
    top_similarity = similarity[word_id]
    
    # 表示
    print(top_word + ': ' + str(top_similarity))
    
    # 表示した単語数をカウント
    count += 1
    
    # 指定した回数に達するとストップ
    if count >= top:
        break

woman: 5.5012217
king: 4.143792
horse: 3.8625212
hat: 3.8558233
artist: 3.8515666
pages: 3.8278775
mile: 3.730414
bike: 3.6934948
lexington: 3.6756523
duck: 3.6472259

　以上で類推問題の答えの可能性の高い単語が出力できました。これが基本的な処理になります。ただしこのままでは問題として指定した単語も表示されてしまう可能性があるため、実装時にはそれを飛ばす処理などを加えます。

・実装

　処理の確認ができたので、類推問題を関数として実装します。

# 類推問題の実装
def analogy(a, b, c, word_to_id, id_to_word, word_matrix, top=5, answer=None):
    # 単語ベクトルが存在するか検索
    for word in (a, b, c):
        if word not in word_to_id:
            print('%s is not found' % word)
            return
    
    # 類推問題を表示
    print('\n[analogy] ' + a + ':' + b + ' = ' + c + ':?')
    
    # 単語ベクトルを取得
    a_vec, b_vec, c_vec = word_matrix[word_to_id[a]], word_matrix[word_to_id[b]], word_matrix[word_to_id[c]]
    
    # 求めたい単語のベクトルを計算
    query_vec = b_vec - a_vec + c_vec
    query_vec = normalize(query_vec) #正規化:式(2.1')
    
    # 全ての単語とのコサイン類似度を計算:式(2.1)
    similarity = np.dot(word_matrix, query_vec)
    
    # (想定される)答の単語のベクトルを表示
    if answer is not None:
        print("==>" + answer + ":" + str(np.dot(word_matrix[word_to_id[answer]], query_vec)))
    
    # 類似度の上位単語を表示
    count = 0
    for i in (-1 * similarity).argsort():
        # NaNまたは問題の単語の場合はパス
        if np.isnan(similarity[i]):
            continue
        if id_to_word[i] in (a, b, c):
            continue
        
        # 単語とコサイン類似度を表示
        print(' {0}: {1}'.format(id_to_word[i], similarity[i]))

        # 表示した単語の数が指定を超えたらストップ
        count += 1
        if count >= top:
            return

　実装した関数を試してみましょう。

# 類推
analogy('man', 'king', 'woman', word_to_id, id_to_word, word_matrix=word_vecs, top=5, answer='queen')

[analogy] man:king = woman:?
==>queen:2.004106
 horse: 3.862521171569824
 hat: 3.855823278427124
 artist: 3.8515665531158447
 pages: 3.8278775215148926
 mile: 3.7304139137268066

# 類推
analogy('take', 'took', 'go', word_to_id, id_to_word, word_matrix=word_vecs, top=5, answer='went')

[analogy] take:took = go:?
==>went:4.205059
 eurodollars: 5.448766708374023
 was: 4.683789253234863
 were: 4.399063587188721
 're: 4.302835941314697
 went: 4.205059051513672

# 類推
analogy('car', 'cars', 'child', word_to_id, id_to_word, word_matrix=word_vecs, top=5, answer='children')

[analogy] car:cars = child:?
==>children:5.334798
 a.m: 6.520125865936279
 rape: 5.623735427856445
 children: 5.334797382354736
 women: 4.878530502319336
 males: 4.6318864822387695

# 類推
analogy('good', 'better', 'bat', word_to_id, id_to_word, word_matrix=word_vecs, top=5, answer='worse')

[analogy] good:better = bat:?
==>worse:2.4815502
 less: 5.265024185180664
 more: 4.368565082550049
 bit: 4.3663177490234375
 lot: 3.8593664169311523
 rather: 3.75911808013916

　word2vecを使って類推問題を解けたり解けなかったりしました！

　以上で4章の内容は終了です。3章と4章ではCBOWモデルを学びました。次章ではRNNを扱います。

参考文献

• 斎藤康毅『ゼロから作るDeep Learning 2――自然言語処理編』オライリー・ジャパン,2018年.

おわりに

　今月は他の本も並行して進めていたため更新が途切れ途切れになってしまいましたが、これで4章完了です。次章もぼちぼち進めるつもりです。

【次節の内容】

www.anarchive-beta.com