はじめに
『ゼロから作るDeep Learning 2――自然言語処理編』の初学者向け【実装】攻略ノートです。『ゼロつく2』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
本の内容を1つずつ確認しながらゆっくりと組んでいきます。
この記事は、1.4節「ニューラルネットワークで問題を解く」の内容です。2層のニューラルネットワークをPythonで実装して、学習と分類を行います。
【前節の内容】
【他の節の内容】
【この節の内容】
1.4.1 スパイラル・データセット
マスターデータからスパイラルデータセットを読み込みます。
「deep-learning-from-scratch-2-master」フォルダのファイルパスをsys.path.append()に指定して、「dataset」フォルダの「spiral.py」ファイルに実装されているデータ読み込み関数をインポートします。
# データ読み込み用の設定 import sys sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master') # スパイラル・データセット読み込み関数をインポート from dataset import spiral # その他この節で利用するライブラリ import numpy as np import matplotlib.pyplot as plt
スパイラルデータセットを読み込みます。
# スパイラル・データセットを読み込む x, t = spiral.load_data() print(x.shape) print(t.shape)
(300, 2)
(300, 3)
データの一部を確認しましょう。
print(x[96:105]) print(t[96:105])
[[-0.78313528 -0.55524691]
[-0.68338075 -0.68839723]
[-0.6793856 -0.70628267]
[-0.58700916 -0.79719524]
[-0. -0. ]
[-0.00837021 -0.00547171]
[-0.01839967 -0.00783914]
[-0.02386156 -0.01818313]
[-0.0271639 -0.02936192]]
[[1 0 0]
[1 0 0]
[1 0 0]
[1 0 0]
[0 1 0]
[0 1 0]
[0 1 0]
[0 1 0]
[0 1 0]]
教師データtを全て確認すると分かりますが、0から99までがクラス1のデータ、100から199がクラス2、200から299がクラス3となっています。
可視化してみましょう。
plt.scatter()で散布図を描きます。第1引数(x軸)にxの0列目、2引数(y軸)にxの1列目を指定します。
行インデックスとしてi*N:(i+1)*Nとすることで、スライスで各クラスのデータを(100ずつ3回に分けて)抽出できます。
# 各クラスのデータ数 N = 100 # クラス数 class_num = 3 # 各クラスのマーカーを指定 markers = ['o', 'x', '^'] # 作図 for i in range(class_num): plt.scatter(x[i*N:(i+1)*N, 0], x[i*N:(i+1)*N, 1], marker=markers[i]) # 散布図 plt.title('Spiral Data Set', fontsize=20) # タイトル plt.show() # 描画

クラスごとにまとまりがあることが分かります(図1-31)。なのでそれぞれまとまりの付近のデータを観測した場合、同じクラスであることが予想されます。ただし各クラスの領域は渦巻き状(非線形)であるため、直線で区分けすることができません。
この3つのクラスをニューラルネットワークを使って分類します。
1.4.2 ニューラルネットワークの実装
これまでに実装したクラスを用いて、順伝播メソッドと逆伝播メソッドを持つ2層のニューラルネットワークをクラスとして実装します。
基本的な構造は1.2.2項の実装と同じです。
各レイヤのインスタンスをリストに格納し、インスタンス変数layersとして保持します。ただし推論(クラス分類)では正規化(確率への変換)や損失の計算をする必要がありません。そののためSoftmax with Lossレイヤのインスタンスは、別のインスタンス変数los_layerとして保持します。
順伝播メソッドでは、推論メソッド.predict()でスコアを計算し、SoftmaxWithLossクラスの順伝播メソッドで交差エントロピー誤差を計算します。
逆伝播メソッドでは、まずSoftmaxWithLossクラスの逆伝播メソッドで勾配doutを計算し、更にreversed()でリストの後の要素(各レイヤのインスタンス)から逆順に処理し、繰り返し勾配doutを更新します。
# 2層ニューラルネットワークの実装 class TwoLayerNet: # 初期化メソッドの定義 def __init__(self, input_size, hidden_size, output_size): # 各レイヤのニューロン数 I, H, O = input_size, hidden_size, output_size # 各レイヤのパラメータの初期値を生成 W1 = 0.01 * np.random.randn(I, H) b1 = np.zeros(H) W2 = 0.01 * np.random.randn(H, O) b2 = np.zeros(O) # レイヤを生成しリストに格納 self.layers = [ Affine(W1, b1), Sigmoid(), Affine(W2, b2) ] # 最終層の活性化レイヤとLossレイヤ self.loss_layer = SoftmaxWithLoss() # レイヤごとにパラメータと勾配をリストに格納 self.params = [] # パラメータを初期化 self.grads = [] # 勾配を初期化 for layer in self.layers: self.params += layer.params self.grads += layer.grads # 推論メソッドの定義 def predict(self, x): # レイヤごとに順伝播メソッドを実行 for layer in self.layers: x = layer.forward(x) return x # 順伝播(lossの計算)メソッドの定義 def forward(self, x, t): # スコアを計算 score = self.predict(x) # 交差エントロピー誤差を計算 loss = self.loss_layer.forward(score, t) return loss # 逆伝播(勾配の計算)メソッドの定義 def backward(self, dout=1): # lossレイヤの勾配を計算 dout = self.loss_layer.backward(dout) # 後のレイヤから逆伝播メソッドを実行 for layer in reversed(self.layers): # リストの逆順に dout = layer.backward(dout) return dout
各レイヤの入力x($\mathbf{x}$)・勾配dout($\frac{\partial L}{\partial \mathbf{x}}$)が、次のレイヤの順伝播.forward()・逆伝播.backward()の引数に渡され(伝播し)、その計算結果がx・doutの値に反映され、更に次のレイヤに伝播していることがプログラムからも実感できますね。
次項では、実装したクラスを用いて学習を行います。
1.4.3 学習用のソースコード
データセットを読み込み、ニューラルネットワークを構築できたので、学習と推論(分類)を行います。
ハイパーパラメータを指定します。
# データセット当たりの試行回数を指定 max_epoch = 300 # バッチサイズを指定 batch_size = 30 # 中間層のニューロン数を指定 hidden_size = 10 # 学習率を指定 learning_rate = 1.0 # データ数を取得 data_size = len(x) print(data_size) # バッチデータ当たりの試行回数を計算 max_iters = data_size // batch_size print(max_iters)
300
10
2層のニューラルネットワークのクラスと最適化手法のクラスのインスタンスを作成します。この例ではSGDにより学習を行います。
# ニューラルネットワークのインスタンスを作成 model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3) # 最適化手法のインスタンスを作成 optimizer = SGD(lr=learning_rate)
学習したパラメータはmodelに保存されているため、学習をやり直す際はここから再実行して値を初期化する必要があります。
始めにデータセットをランダムに並べ変えます。そこからバッチサイズのデータを順番に取り出して、学習を行います。データを入れ替えることで勾配も変化し、効率的な学習を行えます。
学習の処理は、これまでに確認した通りです。
学習が進み具合を確認するために、損失lossを記録しておきます。ただし毎回記録するのではなく、10回ごとに損失の平均を記録することにします。total_lossにlossの値を加えます。またその度にloss_countに1を加えることで、加算した回数を記録します。指定した回数ごとにtotal_lossをtotal_lossで割ることで、平均損失avg_lossを求めます。求めた平均損失を.append()でリストに格納していきます。その後、total_lossにlossとloss_countを初期化する必要があります。
# 平均loss算出用変数を初期化 total_loss = 0 loss_count = 0 # lossの推移記録用のリストを初期化 loss_list = [] # エポックごとの処理 for epoch in range(max_epoch): # データセットをシャッフル idx = np.random.permutation(data_size) # ランダムにインデックスを生成 x = x[idx] t = t[idx] # ミニバッチデータごとに学習 for iters in range(max_iters): # バッチデータを抽出 batch_x = x[iters*batch_size:(iters+1)*batch_size] batch_t = t[iters*batch_size:(iters+1)*batch_size] # 交差エントロピー誤差を計算 loss = model.forward(batch_x, batch_t) # 勾配を計算 model.backward(dout=1) # パラメータを更新 optimizer.update(model.params, model.grads) # カウント total_loss += loss loss_count += 1 # 10回ごとに表示 if (iters + 1) % 10 == 0: # 平均lossを計算 avg_loss = total_loss / loss_count print( '| epoch %d | iter %d / %d | loss %.2f' % (epoch + 1, iters + 1, max_iters, avg_loss) ) loss_list.append(avg_loss) # 値を記録 total_loss, loss_count = 0, 0 # 初期化
| epoch 1 | iter 10 / 10 | loss 1.13
| epoch 2 | iter 10 / 10 | loss 1.13
| epoch 3 | iter 10 / 10 | loss 1.12
| epoch 4 | iter 10 / 10 | loss 1.12
| epoch 5 | iter 10 / 10 | loss 1.11
(省略)
| epoch 296 | iter 10 / 10 | loss 0.11
| epoch 297 | iter 10 / 10 | loss 0.12
| epoch 298 | iter 10 / 10 | loss 0.11
| epoch 299 | iter 10 / 10 | loss 0.11
| epoch 300 | iter 10 / 10 | loss 0.11
途中経過の表示については「%記法」や「%演算子」辺りでググってください。
loss_listに記録した損失の推移をグラフで確認しましょう。
# 作図 plt.plot(np.arange(len(loss_list)), loss_list, label='train') # 点の位置 plt.xlabel('iterations (x10)') # x軸ラベル plt.ylabel('loss') # y軸ラベル plt.title('Cross Entropy Loss', fontsize=20) # タイトル plt.show() # 表示
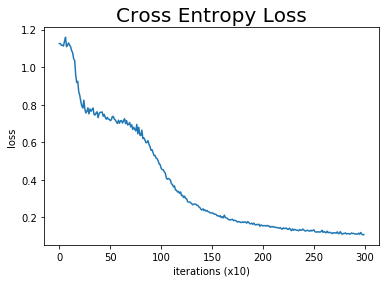
損失(交差エントロピー誤差)は、全てのデータを正しく分類できたとき値が0になります。この例ではほぼ0まで下がったことから、データセットに対して学習できたと言えます(図1-32)。
次は、正しくクラス分類ができていることを散布図(図1-31)を用いて確認しましょう。
まずは入力データに対応する、細かな格子状の点を生成します。
データセットの最小値-0.1、最大値+0.1をx軸とy軸それぞれの範囲とし、指定した間隔の数値列を生成します。それnp.meshgrid()の第1引数と第2引数に指定することで、格子状の点(直交する点)を生成します。列方向に値が変化する変数xxと行方向に値が変化する変数yyが生成されます。
この例のニューラルネットワークは、入力が要素数が2のデータである必要があるため、xxとyyを.ravel()で1列に並べ替え、np.c_[]で列方向に結合します。
# 点の間隔を指定 h = 0.001 # x軸の点を生成 x_min = x[:, 0].min() - 0.1 x_max = x[:, 0].max() + 0.1 x_vec = np.arange(x_min, x_max, h) # y軸の点を生成 y_min = x[:, 1].min() - 0.1 y_max = x[:, 1].max() + 0.1 y_vec = np.arange(y_min, y_max, h) # 格子状の点を生成 xx, yy = np.meshgrid(x_vec, y_vec) print(np.round(xx[0:5, 0:5], 3)) print(xx.shape) print(np.round(yy[0:5, 0:5], 3)) print(yy.shape) # リストを結合 X = np.c_[xx.ravel(), yy.ravel()] print(np.round(X[0:5, :], 3)) print(X.shape)
[[-1.022 -1.021 -1.02 -1.019 -1.018]
[-1.022 -1.021 -1.02 -1.019 -1.018]
[-1.022 -1.021 -1.02 -1.019 -1.018]
[-1.022 -1.021 -1.02 -1.019 -1.018]
[-1.022 -1.021 -1.02 -1.019 -1.018]]
(2047, 2112)
[[-0.989 -0.989 -0.989 -0.989 -0.989]
[-0.988 -0.988 -0.988 -0.988 -0.988]
[-0.987 -0.987 -0.987 -0.987 -0.987]
[-0.986 -0.986 -0.986 -0.986 -0.986]
[-0.985 -0.985 -0.985 -0.985 -0.985]]
(2047, 2112)
[[-1.022 -0.989]
[-1.021 -0.989]
[-1.02 -0.989]
[-1.019 -0.989]
[-1.018 -0.989]]
(4323264, 2)
Xは、図1-32の描画範囲をh間隔で満遍なく並べたデータ(点)です。つまり全ての位置のクラスを推論し、そのクラスごとに色分けすることで境界を可視化します。
学習済みのパラメータを用いて、生成した各データのクラスを推論します。各データのスコアの最大値のインデックスがクラスの値に対応します。
# スコアを計算 score = model.predict(X) print(score[0:5]) # 推論結果(各データのクラス)を抽出 predict_cls = np.argmax(score, axis=1) print(predict_cls[0:5]) # 形状を調整 Z = predict_cls.reshape(xx.shape) print(Z)
[[ 7.0750414 -6.07991423 -1.0589919 ]
[ 7.07900866 -6.07605854 -1.06679914]
[ 7.08296037 -6.07223889 -1.07455478]
[ 7.08689655 -6.06845546 -1.08225869]
[ 7.09081721 -6.0647084 -1.0899107 ]]
[0 0 0 0 0]
[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
...
[2 2 2 ... 1 1 1]
[2 2 2 ... 1 1 1]
[2 2 2 ... 1 1 1]]
ちなみに0から4番目のデータは図の左下の点です。つまり青丸(クラス0)の領域です。
スパイラルデータセットはシャッフルしたため、クラスごとにマーカ-を変えて描画するのが手間です。そこでデータセットを読み込み直します。
# データセットを再読み込み x, t = spiral.load_data() # 各クラスのデータ数 N = 100 # クラス数 CLS_NUM = 3
図1-32の散布図に、推定したクラスを塗りつぶし等高線として重ねて描画します。
xxはx軸の値、yyはy軸の値、Zはz軸の値に対応します。またZは、0か1か2の値をとります。このZの値に従って、plt.contourf()で塗りつぶし等高線を描きます。
# 等高線グラフ plt.contourf(xx, yy, Z) # 塗りつぶし等高線図 #plt.axis('off') # 軸の表示 # 各クラスのマーカーを指定 markers = ['o', 'x', '^'] for i in range(CLS_NUM): plt.scatter(x[i*N:(i+1)*N, 0], x[i*N:(i+1)*N, 1], marker=markers[i]) # 散布図 plt.title('Spiral Data Set', fontsize=20) # タイトル plt.show() # 描画

非線形な分類ができていることを確認できました!
今後もこのように学習を進めるため、次項では学習処理をクラスとして実装します。
1.4.4 Trainerクラス
1.4.3項で行った学習の処理をまとめてクラスとして実装しましょう。
現段階ではclip_grads()とremove_duplicate()については実装せずにインポートすることにします。
# クラスに利用するライブラリ import numpy as np import matplotlib.pyplot as plt import time # 処理時間計測用 # データ読み込み用の設定 import sys sys.path.append('C://Users//「ユーザー名」//Documents//・・・//deep-learning-from-scratch-2-master') from common.util import clip_grads # from common.trainer import remove_duplicate #
では学習処理をクラスとして実装します。
# 学習 class Trainer: # 初期化メソッドの定義 def __init__(self, model, optimizer): self.model = model # ニューラルネットワークのインスタンス self.optimizer = optimizer # 最適化手法のインスタンス self.loss_list = [] # 損失の記録用リスト self.eval_interval = None # 平均損失を求めるイタレーション数 self.current_epoch = 0 # 現在の試行回数 # 学習メソッドの定義 def fit(self, x, t, max_epoch=10, batch_size=32, max_grad=None, eval_interval=20): data_size = len(x) # データ数 max_iters = data_size // batch_size # 1データあたりの試行回数 self.eval_interval = eval_interval # 平均損失を求めるイタレーション数 model = self.model # ニューラルネットワークのインスタンス optimizer = self.optimizer # # 最適化手法のインスタンス total_loss = 0 # (平均損失計算用)損失の合計 loss_count = 0 # (平均損失計算用)損失を加算した回数 # エポックごとに処理 start_time = time.time() # 処理の開始時間を記録 for epoch in range(max_epoch): # データセットをシャッフル idx = np.random.permutation(np.arange(data_size)) # ランダムにインデックスを生成 x = x[idx] t = t[idx] # バッチデータごとに学習 for iters in range(max_iters): # バッチデータを取得 batch_x = x[iters*batch_size:(iters+1)*batch_size] batch_t = t[iters*batch_size:(iters+1)*batch_size] # 損失を計算(順伝播) loss = model.forward(batch_x, batch_t) # 勾配を計算(逆伝播) model.backward() # パラメータに関する何か params, grads = remove_duplicate(model.params, model.grads) # L2ノルムに関する何か if max_grad is not None: clip_grads(grads, max_grad) # パラメータを更新 optimizer.update(params, grads) # (一定期間の)平均損失の計算用に記録 total_loss += loss loss_count += 1 # if (eval_interval is not None) and ((iters + 1) % eval_interval) == 0: # 平均損失を計算 avg_loss = total_loss / loss_count # 処理時間を計算 elapsed_time = time.time() - start_time # 表示 print( '| epoch %d | iter %d / %d | time %d[s] | loss %.2f' % (self.current_epoch + 1, iters + 1, max_iters, elapsed_time, avg_loss) ) # 平均損失を記録 self.loss_list.append(float(avg_loss)) total_loss, loss_count = 0, 0 # 初期化 # 処理したエポック数をカウント self.current_epoch += 1 # 交差エントロピー誤差の推移のグラフ化メソッドの定義 def plot(self, ylim=None): # x軸の値を生成 x = np.arange(len(self.loss_list)) # 作図 if ylim is not None: # 引数に指定されたとき plt.ylim(*ylim) # y軸の範囲 plt.plot(x, self.loss_list, label='train') # 点の位置 plt.xlabel('iterations (x' + str(self.eval_interval) + ')') # x軸ラベル plt.ylabel('loss') # y軸ラベル plt.title('Cross Entropy Error', fontsize=20) # タイトル plt.show() # 描画
ではこのクラスを使って前項と同じことをしてみましょう。
まずはデータセットを読み込みます。
# スパイラル・データセット読み込み関数をインポート from dataset import spiral # スパイラル・データセットを読み込む x, t = spiral.load_data() print(x.shape) print(t.shape)
(300, 2)
(300, 3)
1.4.2項で作成した2層のニューラルネットワークのインスタンスを作成します。
# 中間層のニューロン数を指定 hidden_size = 10 # データ数を取得 data_size = len(x) print(data_size) # ニューラルネットワークのインスタンスを作成 model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
300
最適化手法のインスタンスを作成します。この例では、1.3.6項で実装した確率的勾配降下法SGDを用います。
# 学習率を指定 learning_rate = 1.0 # 最適化手法のインスタンスを作成 optimizer = SGD(lr=learning_rate)
Trainerのインスタンスを作成します。第1引数にニューラルネットワーク、第2引数に最適化手法のインスタンスを指定します。
# 学習処理のインスタンスを作成
trainer = Trainer(model, optimizer)
学習を行います。
# データセット当たりの試行回数を指定 max_epoch = 300 # バッチサイズを指定 batch_size = 30 # 学習 trainer.fit( x=x, # 入力データ t=t, # 教師データ max_epoch=max_epoch, batch_size=batch_size, eval_interval=10 # 推移の確認用のイタレーション数 )
| epoch 1 | iter 10 / 10 | time 0[s] | loss 1.13
| epoch 2 | iter 10 / 10 | time 0[s] | loss 1.13
| epoch 3 | iter 10 / 10 | time 0[s] | loss 1.12
| epoch 4 | iter 10 / 10 | time 0[s] | loss 1.12
| epoch 5 | iter 10 / 10 | time 0[s] | loss 1.11
(省略)
| epoch 296 | iter 10 / 10 | time 0[s] | loss 0.11
| epoch 297 | iter 10 / 10 | time 0[s] | loss 0.12
| epoch 298 | iter 10 / 10 | time 0[s] | loss 0.11
| epoch 299 | iter 10 / 10 | time 0[s] | loss 0.11
| epoch 300 | iter 10 / 10 | time 0[s] | loss 0.11
指定したイタレーション数の平均損失(交差エントロピー誤差)の推移をグラフ化します。
# 作図
trainer.plot()
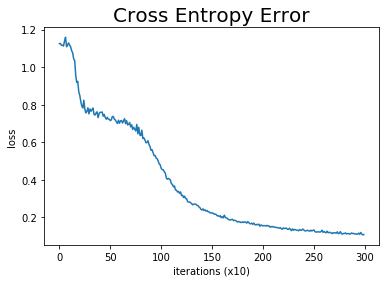
図1-32のグラフを再現できました。
学習の処理もクラスとしてまとめることで、コードがスッキリするとともに、無用なミスも回避できますね。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning 2――自然言語処理編』オライリー・ジャパン,2018年.
おわりに
1章終了!とりあえず順調です。しかしブログにまとめてると、理解は進みますが本編が進まないのでもどかしいです。
【次節の内容】