はじめに
「機械学習・深層学習」学習初手『ゼロから作るDeep Learning』民のための数学攻略ノートです。『ゼロつく1』学習の補助となるように適宜解説を加えています。本と一緒に読んでください。
NumPy関数を使って実装できてしまう計算について、数学的背景を1つずつ確認していきます。
この記事は、主に3.2.1項「シグモイド関数」を補足するための内容になります。指数関数のごく基礎的な定義をグラフを描くことで説明します。
【関連する記事】
【他の記事一覧】
【この記事の内容】
・指数関数(1):指数関数とは
# 利用するライブラリ import numpy as np import matplotlib.pyplot as plt
指数関数とは、定数$a$を$x$乗したものです。ただし$a > 0,\ a \neq 1$です(1を何乗しても1のままなので除きます)。$a$を底と言います。(早く$\exp(\cdot)$が知りたければネイピア数まで飛ばしてもいいです。)
実際に計算して、その結果をプロットしてみましょう。
# 底を指定 a = 2 # x軸の値を生成 x = np.arange(-5, 5, 0.1) # 指数関数の計算 y = a ** x print(np.round(y, 2))
[ 0.03 0.03 0.04 0.04 0.04 0.04 0.05 0.05 0.05 0.06 0.06 0.07
0.07 0.08 0.08 0.09 0.09 0.1 0.11 0.12 0.12 0.13 0.14 0.15
0.16 0.18 0.19 0.2 0.22 0.23 0.25 0.27 0.29 0.31 0.33 0.35
0.38 0.41 0.44 0.47 0.5 0.54 0.57 0.62 0.66 0.71 0.76 0.81
0.87 0.93 1. 1.07 1.15 1.23 1.32 1.41 1.52 1.62 1.74 1.87
2. 2.14 2.3 2.46 2.64 2.83 3.03 3.25 3.48 3.73 4. 4.29
4.59 4.92 5.28 5.66 6.06 6.5 6.96 7.46 8. 8.57 9.19 9.85
10.56 11.31 12.13 13. 13.93 14.93 16. 17.15 18.38 19.7 21.11 22.63
24.25 25.99 27.86 29.86]
# 作図 plt.plot(x, y) plt.title("Exponential Function", fontsize = 20) plt.show()

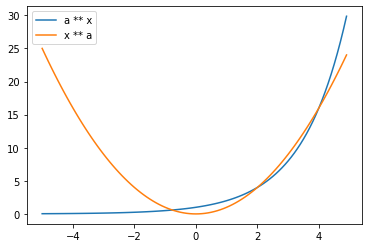
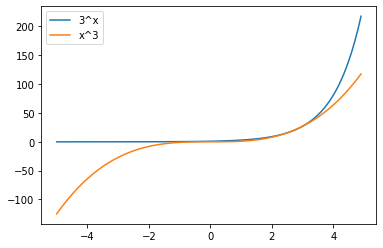
おまけで$y = x^a$のグラフと重ねてみましょうか。
# 作図 plt.plot(x, y, label = "a ** x") # 指数関数 plt.plot(x, x ** a, label = "x ** a") # n次関数 plt.legend() # 凡例 plt.show()
続いて、$a$にネイピア数を用いる場合を考えます。
・ネイピア数
ネイピア数とは特別な値で$e$を使って表します(円周率$\pi$のようなものと思ってください)。
$$ e = 2.7182\cdots $$
何が特別かは自然対数$\log x$までとっておきます(気になる方はシグモイド関数の前に読んでもいいです)。ネイピア数を使った指数関数は次のようになります。
しかしこれでは、注目したい$x$が右肩に小さく表記されていて分かりにくいですね。そこで次のようにも表記します。
式としてはどちらも同じものです。以降は本もノートもこちらの表記を用います。
では実際の計算結果とグラフでも確認しましょう。
# ネイピア数 e = 2.7182 # x軸の値を生成 x = np.arange(-5.0, 5.0, 0.1) # 指数関数の計算 y = e ** x print(y)
[6.73896125e-03 7.44768157e-03 8.23093631e-03 9.09656405e-03
1.00532278e-02 1.11105015e-02 1.22789662e-02 1.35703155e-02
1.49974729e-02 1.65747210e-02 1.83178445e-02 2.02442881e-02
2.23733311e-02 2.47262804e-02 2.73266837e-02 3.02005653e-02
3.33766859e-02 3.68868316e-02 4.07661308e-02 4.50534066e-02
4.97915649e-02 5.50280238e-02 6.08151885e-02 6.72109754e-02
7.42793918e-02 8.20911765e-02 9.07245077e-02 1.00265786e-01
1.10810497e-01 1.22464170e-01 1.35343432e-01 1.49577174e-01
1.65307845e-01 1.82692873e-01 2.01906243e-01 2.23140236e-01
2.46607357e-01 2.72542459e-01 3.01205092e-01 3.32882107e-01
3.67890516e-01 4.06580675e-01 4.49339785e-01 4.96595768e-01
5.48821549e-01 6.06539789e-01 6.70328118e-01 7.40824911e-01
8.18735682e-01 9.04840142e-01 1.00000000e+00 1.10516759e+00
1.22139540e+00 1.34984662e+00 1.49180673e+00 1.64869645e+00
1.82208589e+00 2.01371027e+00 2.22548733e+00 2.45953647e+00
2.71820000e+00 3.00406655e+00 3.31999699e+00 3.66915307e+00
4.05502906e+00 4.48148670e+00 4.95279386e+00 5.47366726e+00
6.04931967e+00 6.68551204e+00 7.38861124e+00 8.16565369e+00
9.02441581e+00 9.97349189e+00 1.10223800e+01 1.21815772e+01
1.34626843e+01 1.48785224e+01 1.64432607e+01 1.81725588e+01
2.00837231e+01 2.21958798e+01 2.45301671e+01 2.71099456e+01
2.99610333e+01 3.31119630e+01 3.65942684e+01 4.04427995e+01
4.46960713e+01 4.93966494e+01 5.45915761e+01 6.03328406e+01
6.66779001e+01 7.36902543e+01 8.14400808e+01 9.00049379e+01
9.94705404e+01 1.09931618e+02 1.21492861e+02 1.34269972e+02]
# 作図 plt.plot(x, y) plt.title("Exponential Function", fontsize = 20) plt.show()
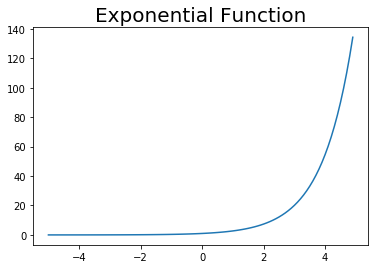
(y軸の値は違いますが)同じ形ですね。
ところで、便利で特別なものは関数として用意されているものです。
ネイピア数$e$はnp.e、ネイピア数を使った指数関数の計算はnp.exp()で行えます(どちらもNumPyライブラリのものです)。
# ネイピア数 print(np.e)
2.718281828459045
# xの値を生成 x = np.arange(-5.0, 5.0, 0.1) # 指数関数の計算 y = np.exp(x) # 作図 plt.plot(x, y) plt.title("Exponential Function", fontsize = 20) plt.show()
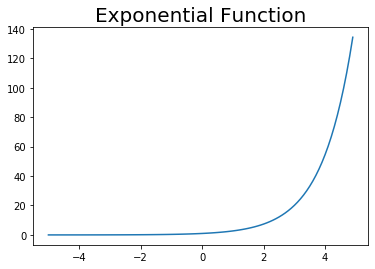
当然同じグラフになります。
指数関数の基礎のキは以上です。どんな性質なのかは(3.5節のソフトマックス関数のところで)自然対数$\log x$とセットで確認します。
参考文献
- 斎藤康毅『ゼロから作るDeep Learning』オライリー・ジャパン,2016年.
- 加藤公一『機械学習のエッセンス』SBクリエイティブ,2018年.
おわりに
何だか記事が短くて気になります。一応本を進めるのに必要な知識のみに留めるというコンセプトなのでこんなこともあります。
【元の記事】