はじめに
機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に自分の理解の助けになったことや勉強会資料のまとめです。トピックモデルの各種アルゴリズムを「数式」と「プログラム」から理解することを目指します。
この記事は、3.4節「変分ベイズ推定」の内容です。
変分ベイズ推定による混合ユニグラムモデルにおけるパラメータ推定を実装します。
【数式編】
【前節の内容】
【他の節一覧】
【この節の内容】
3.4 変分ベイズ推定
アルゴリズム3.2を参考にして、混合ユニグラムモデル(混合カテゴリ分布)に対する変分ベイズ推定を実装する。
この記事では、3重のループを使って実装する。「【R】3.4:混合ユニグラムモデルの変分ベイズ推定の実装:ループなし版【『トピックモデル』の勉強ノート】 - からっぽのしょこ」では、行列計算を使って、ループを使わずに実装する。簡潔に計算(処理)したい場合は「ループなし版」を参照のこと。
利用するパッケージを読み込む。
# 利用パッケージ library(tidyverse) library(gganimate) library(gtools)
この記事では、基本的にパッケージ名::関数名()の記法を使うので、パッケージを読み込む必要はない。ただし、作図コードに関してはパッケージ名を省略するので、ggplot2を読み込む必要がある。
また、magrittrパッケージのパイプ演算子%>%ではなく、ネイティブパイプ演算子|>を使う。%>%に置き換えても処理できるが、その場合はmagrittrを読み込む必要がある。
文書データの簡易生成
混合ユニグラムモデルでは、トピック分布(カテゴリ分布)に従い文書ごとにトピックが割り当てられ、さらにトピックに応じた単語分布(カテゴリ分布)に従い単語が出現していると仮定する。詳しくは「3.1-2:混合ユニグラムモデル【『トピックモデル』の勉強ノート】 - からっぽのしょこ」を参照のこと。
まずは、生成モデル(真のトピック分布と単語分布)を設定して、簡易的に文書データ(bag-of-words)を生成する。
真の分布の設定
文書データに関する値を設定する。
# 文書数を指定 D <- 20 # 語彙数を指定 V <- 26 # トピック数を指定 K <- 4
生成する文書数$D$、語彙(単語の種類)数$V$、トピック数$K$を指定する。
真のトピック分布を作成する。
・コード(クリックで展開)
# 真のトピック分布を生成 theta_true_k <- MCMCpack::rdirichlet(n = 1, alpha = rep(1, times = K)) |> as.vector() theta_true_k
## [1] 0.40817269 0.32534960 0.05573835 0.21073937
ディリクレ分布からカテゴリ分布(のパラメータ)を生成して、真のトピック分布$\boldsymbol{\theta}^{(\mathrm{true})} = (\theta_1^{(\mathrm{true})}, \cdots, \theta_K^{(\mathrm{true})})$、$0 \leq \theta_k^{(\mathrm{true})} \leq 1$、$\sum_{k=1}^K \theta_k^{(\mathrm{true})} = 1$とする。または、値を直接指定する。
ディリクレ分布の乱数は、MCMCpackパッケージのrdirichlet()で生成できる。各トピックの割り当て確率を生成するため、サンプルサイズの引数nに1、パラメータの引数alphaにK個の正の値(ハイパーパラメータ)を指定する。この例では、一様な確率で生成するため、全ての値を1とする。
作図用に、生成した値をデータフレームに格納する。
# 作図用のデータフレームを作成 true_topic_df <- tibble::tibble( topic = factor(1:K), # トピック番号 probability = theta_true_k # 割り当て確率 ) true_topic_df
## # A tibble: 4 × 2 ## topic probability ## <fct> <dbl> ## 1 1 0.408 ## 2 2 0.325 ## 3 3 0.0557 ## 4 4 0.211
因子型の1からKの整数をトピック番号列として、対応する確率とあわせて格納する。
真のトピック分布をグラフで確認する。
# 真のトピック分布を作図 ggplot() + geom_bar(data = true_topic_df, mapping = aes(x = topic, y = probability, fill = topic), stat = "identity", show.legend = FALSE) + # トピック分布 labs(title = "Topic Distribution", subtitle = "truth", x = "k", y = expression(theta[k]))
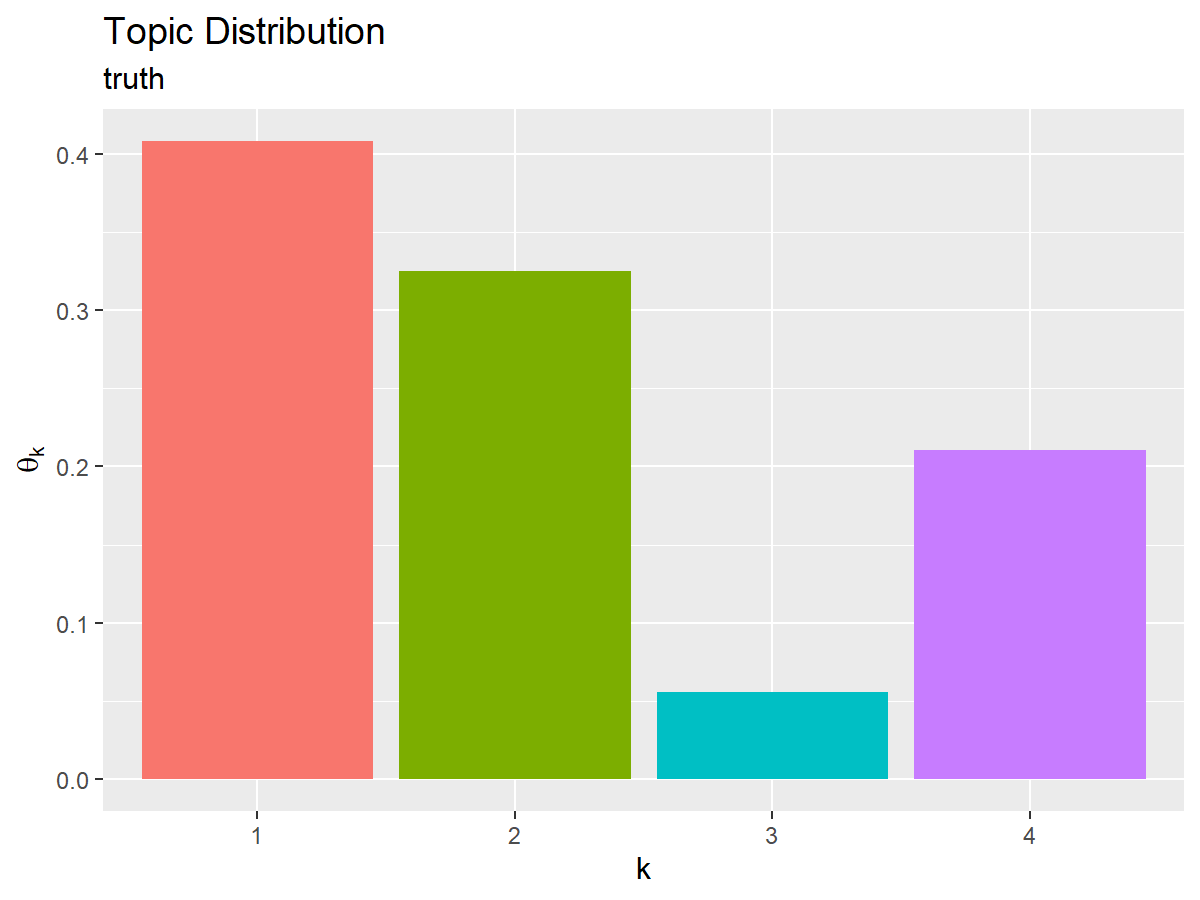
x軸をトピック番号、y軸を各トピックとなる確率として棒グラフを描画する。
同様に、真の単語分布を作成する。
・コード(クリックで展開)
# 真の単語分布を生成 phi_true_kv <- MCMCpack::rdirichlet(n = K, alpha = rep(1, times = V)) phi_true_kv[, 1:5]
phi_true_kv[, 1:5] ## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.09603286 0.00805338 0.036200025 0.05951296 0.078218102 ## [2,] 0.03690758 0.02095619 0.004163542 0.03560467 0.006469918 ## [3,] 0.06739647 0.03640396 0.007794004 0.07180130 0.040110454 ## [4,] 0.04631080 0.01328603 0.017530770 0.01008200 0.081071590
ディリクレ分布からカテゴリ分布(のパラメータ)を生成して、K個の真の単語分布$\boldsymbol{\Phi}^{(\mathrm{true})} = \{\boldsymbol{\phi}_1^{(\mathrm{true})}, \cdots, \boldsymbol{\phi}_K^{(\mathrm{true})}\}$、$\boldsymbol{\phi}_k^{(\mathrm{true})} = (\phi_{k1}^{(\mathrm{true})}, \cdots, \phi_{kV}^{(\mathrm{true})})$、$0 \leq \phi_{kv}^{(\mathrm{true})} \leq 1$、$\sum_{v=1}^V \phi_{kv}^{(\mathrm{true})} = 1$とする。または、値を直接指定する。
こちらは、トピックごとに各語彙の出現確率を生成するため、n引数にトピック数K、alpha引数にV個の正の値(ハイパーパラメータ)を指定する。
生成した値をデータフレームに格納する。
# 作図用のデータフレームを作成 true_word_df <- phi_true_kv |> tibble::as_tibble(.name_repair = ~as.character(1:V)) |> tibble::add_column( topic = factor(1:K) # トピック番号 ) |> tidyr::pivot_longer( cols = !topic, names_to = "vocabulary", # 列名を語彙番号に変換 names_ptypes = list(vocabulary = factor()), values_to = "probability" # 出現確率列をまとめる ) true_word_df
## # A tibble: 104 × 3 ## topic vocabulary probability ## <fct> <fct> <dbl> ## 1 1 1 0.0960 ## 2 1 2 0.00805 ## 3 1 3 0.0362 ## 4 1 4 0.0595 ## 5 1 5 0.0782 ## 6 1 6 0.00207 ## 7 1 7 0.0303 ## 8 1 8 0.0177 ## 9 1 9 0.0953 ## 10 1 10 0.000692 ## # … with 94 more rows
phi_true_kvはK行V列のマトリクスなので、as_tibble()でデータフレームに変換して、トピック番号列を追加する。列名を1からVの整数にしておく。
語彙ごと(V列)の出現確率列をpivot_longer()で1列にまとめる。names_ptypes引数で列名を因子型に変換して、語彙番号列とする。
トピックごとの真の単語分布をグラフで確認する。
# 真の単語分布を作図 ggplot() + geom_bar(data = true_word_df, mapping = aes(x = vocabulary, y = probability, fill = vocabulary), stat = "identity", show.legend = FALSE) + # 単語分布 facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic)), scales = "free_x") + # 分割 labs(title = "Word Distribution", subtitle = "truth", x = "v", y = expression(phi[kv]))
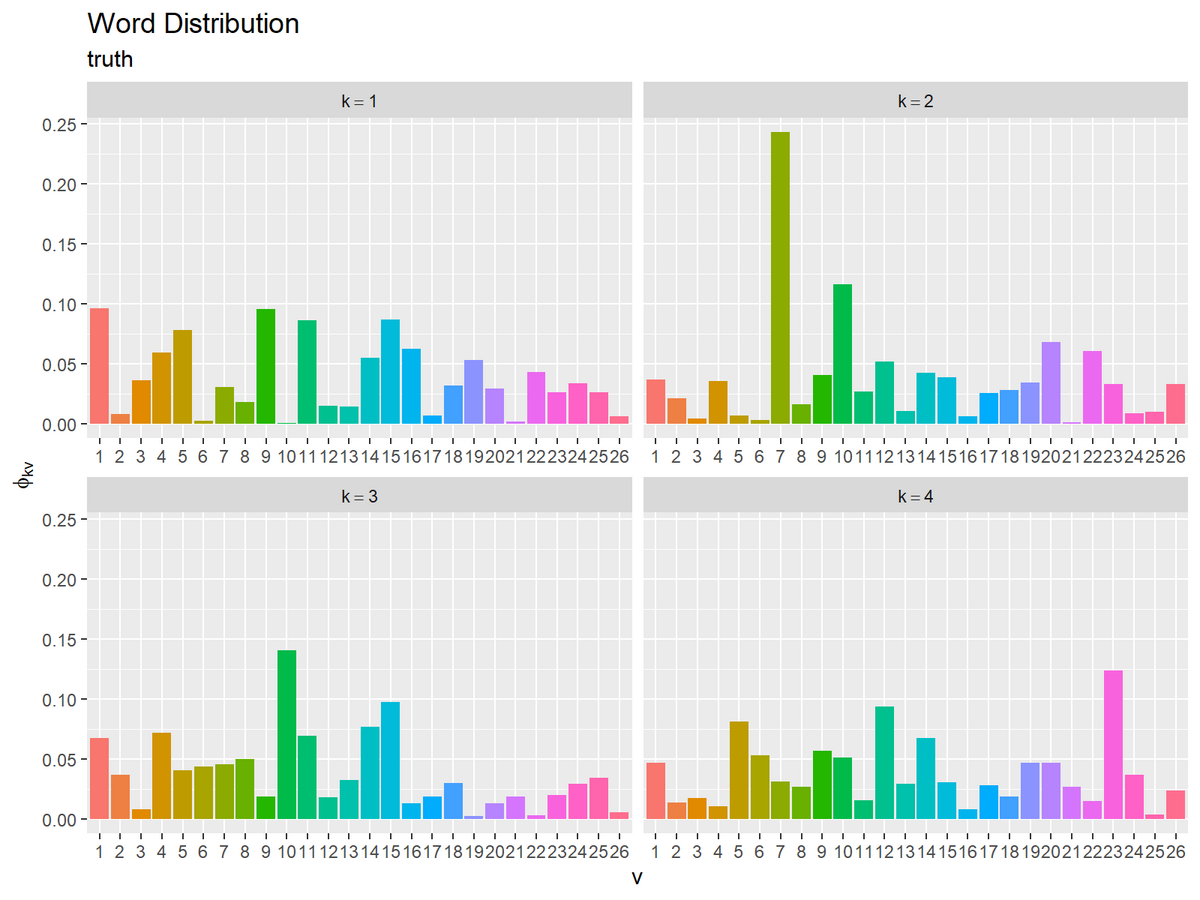
x軸を語彙番号、y軸を各語彙となる確率として棒グラフを描画する。
facet_wrap()にトピック番号列を指定して、トピックごとにグラフを分割して描画する。
文書の生成
設定した生成モデルに従って、文書を生成する。
・コード(クリックで展開)
# 文書を生成 z_d <- rep(NA, times = D) N_d <- rep(NA, times = D) N_dv <- matrix(NA, nrow = D, ncol = V) for(d in 1:D) { # 文書dのトピックを生成 one_hot_k <- rmultinom(n = 1, size = 1, prob = theta_true_k) |> as.vector() k <- which(one_hot_k == 1) # トピック番号を抽出 z_d[d] <- k # 単語数を決定 N_d[d] <- sample(100:200, size = 1) # 範囲を指定 # トピックkに従い単語を生成 N_dv[d, ] <- rmultinom(n = 1, size = N_d[d], prob = phi_true_kv[k, ]) |> as.vector() } z_d[1:5]; N_dv[1:5, 1:5]
## [1] 1 1 1 4 4 ## [,1] [,2] [,3] [,4] [,5] ## [1,] 10 1 5 6 12 ## [2,] 11 3 3 9 9 ## [3,] 14 2 10 10 7 ## [4,] 5 1 3 0 2 ## [5,] 9 2 5 5 21
for()を使って、文書ごとに処理する。
トピック分布(カテゴリ分布)に従いトピックを割り当てる。
カテゴリ分布の乱数は、多項分布の乱数生成関数rmultinom()の試行回数の引数sizeを1にすることで生成できる。サンプルサイズの引数nに1、パラメータの引数probにトピックの割り当て確率theta_true_kを指定する。
one-hotベクトルのトピック(割り当てられたトピック番号に対応する要素が1でそれ以外の要素が0のベクトル)が出力されるので、which()でトピック番号を抽出してkとする。
また確認用に、真のトピックとしてN_dに保存する。
単語数$N_d$をランダムに決めてN_dに保存する。全ての文書で同じ単語数を指定してもよい。
単語ごとに、単語分布(カテゴリ分布)に従い語彙を生成する。この例では、多項分布に従い$N_d$個の単語を1度に生成する。
rmultinom()のsize引数に文書dの単語数N_d[d]、prob引数にトピックkの単語分布phi_true_kv[k, ]を指定する。語彙ごとの出現度数$N_{dv}\ (v = 1,
dots, V)$(総和が$N_d$となるV個の値)が出力されるので、N_dvに保存する。
真のトピックを確認する。
# トピックごとの文書数を確認 table(z_d)
## z_d ## 1 2 3 4 ## 11 4 1 4
各トピックが割り当てられた文書数をtable()で確認できる。
作図用に、文書ごとの出現度数をデータフレームに格納する。
# 作図用のデータフレームを作成 freq_df <- N_dv |> tibble::as_tibble(.name_repair = ~as.character(1:V)) |> tibble::add_column( document = factor(1:D), # 文書番号 word_count = N_d, # 単語数 topic = factor(z_d) # 割り当てトピック ) |> tidyr::pivot_longer( cols = !c(document, word_count, topic), names_to = "vocabulary", # 列名を語彙番号に変換 names_ptypes = list(vocabulary = factor()), values_to = "frequency" # 出現度数列をまとめる ) |> dplyr::mutate( relative_frequency = frequency / N_d[d] # 相対度数 ) freq_df
## # A tibble: 520 × 6 ## document word_count topic vocabulary frequency relative_frequency ## <fct> <int> <fct> <fct> <int> <dbl> ## 1 1 103 1 1 10 0.0526 ## 2 1 103 1 2 1 0.00526 ## 3 1 103 1 3 5 0.0263 ## 4 1 103 1 4 6 0.0316 ## 5 1 103 1 5 12 0.0632 ## 6 1 103 1 6 0 0 ## 7 1 103 1 7 3 0.0158 ## 8 1 103 1 8 2 0.0105 ## 9 1 103 1 9 8 0.0421 ## 10 1 103 1 10 0 0 ## # … with 510 more rows
単語分布のときと同様にして、D行V列のN_dvをデータフレームに変換する。
因子型の1からDの整数を文書番号列、文書ごとの単語数列と真のトピック列を追加する。
pivot_longer()で語彙ごと(V列)の出現度数列を1列にまとめて、列名を語彙番号列に変換する。
文書ごとに、各語彙の度数を単語数で割って相対度数を求める。
各文書の語彙ごとの出現度数をグラフで確認する。
# 度数を作図 ggplot() + geom_bar(data = freq_df, mapping = aes(x = vocabulary, y = frequency, fill = vocabulary), stat = "identity", show.legend = FALSE) + # 出現度数 facet_wrap(document ~ ., labeller = label_bquote(list(d==.(document), N[d]==.(N_d[document]))), scales = "free_x") + # 分割 labs(title = "Word Frequency", x = "v", y = expression(N[dv]))
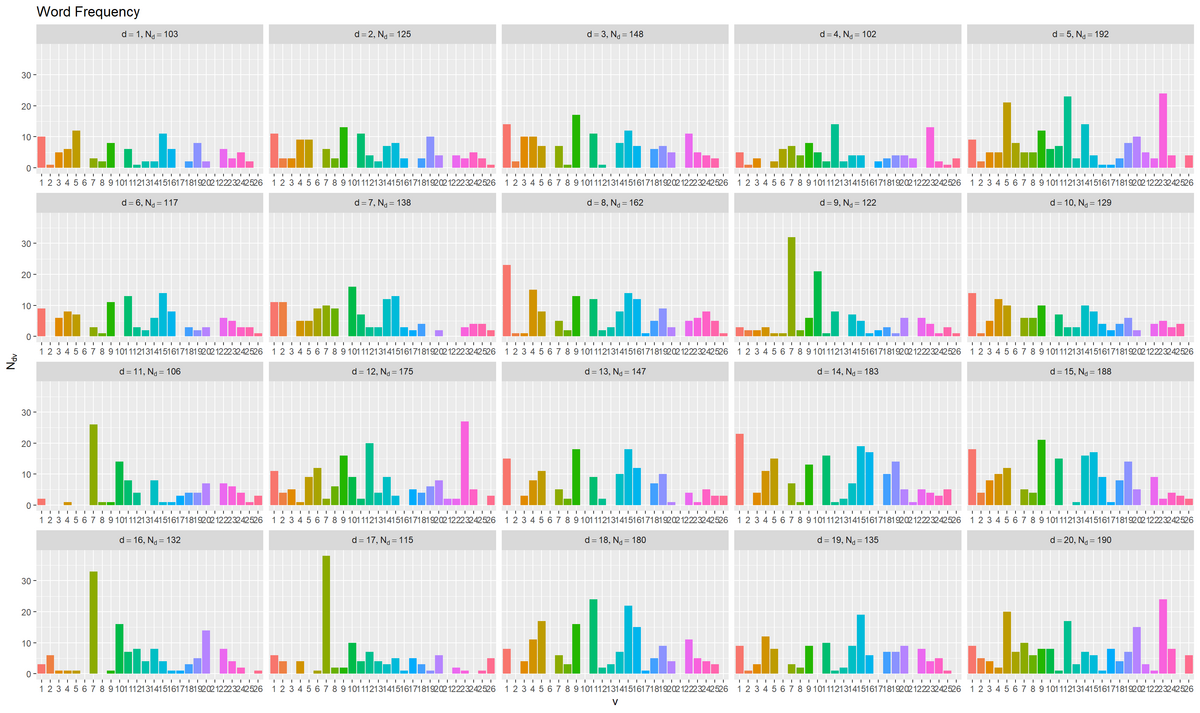
x軸を語彙番号、y軸を各語彙の度数として、文書ごとにグラフを分割して描画する。
・コード(クリックで展開)
確認用に、割り当てられた真のトピックに応じて、単語分布を複製する。
# 真のトピック分布を複製 tmp_word_df <- tidyr::expand_grid( document = factor(1:D), # 文書番号 true_word_df ) |> # 文書数分にトピック分布を複製 dplyr::filter(topic == z_d[document]) # 割り当てられたトピックを抽出 tmp_word_df
## # A tibble: 520 × 4 ## document topic vocabulary probability ## <fct> <fct> <fct> <dbl> ## 1 1 1 1 0.0960 ## 2 1 1 2 0.00805 ## 3 1 1 3 0.0362 ## 4 1 1 4 0.0595 ## 5 1 1 5 0.0782 ## 6 1 1 6 0.00207 ## 7 1 1 7 0.0303 ## 8 1 1 8 0.0177 ## 9 1 1 9 0.0953 ## 10 1 1 10 0.000692 ## # … with 510 more rows
文書番号と単語分布true_word_dfの行の全ての組み合わせをexpand_grid()で作成することで、true_word_dfをD個分に複製する。複製した単語分布(の行)から、真のトピックの単語分布(トピック番号topicが各文書の真のトピックz_d[document]と一致する行)のみを取り出す。
語彙ごとの相対度数を真の単語分布と重ねて描画する。
# 相対度数と真の単語分布を比較 ggplot() + geom_bar(data = freq_df, mapping = aes(x = vocabulary, y = relative_frequency, fill = vocabulary, linetype = "sample"), stat = "identity", alpha = 0.6) + # 出現度数 geom_bar(data = tmp_word_df, mapping = aes(x = vocabulary, y = probability, color = vocabulary, linetype = "truth"), stat = "identity", alpha = 0) + # 単語分布 facet_wrap(document ~ ., labeller = label_bquote(list(d==.(document), z[d]==.(z_d[document]))), scales = "free_x") + # 分割 scale_x_discrete(breaks = 1:V, labels = LETTERS[1:V]) + # x軸目盛:(雰囲気用の演出) scale_linetype_manual(breaks = c("sample", "truth"), values = c("solid", "dashed"), name = "distribution") + # 線の種類:(凡例表示用) guides(color = "none", fill = "none", linetype = guide_legend(override.aes = list(color = c("black", "black"), fill = c("white", "white")))) + # 凡例の体裁:(凡例表示用) labs(title = "Word Frequency", x = "v", y = expression(frac(N[dv], N[d])))
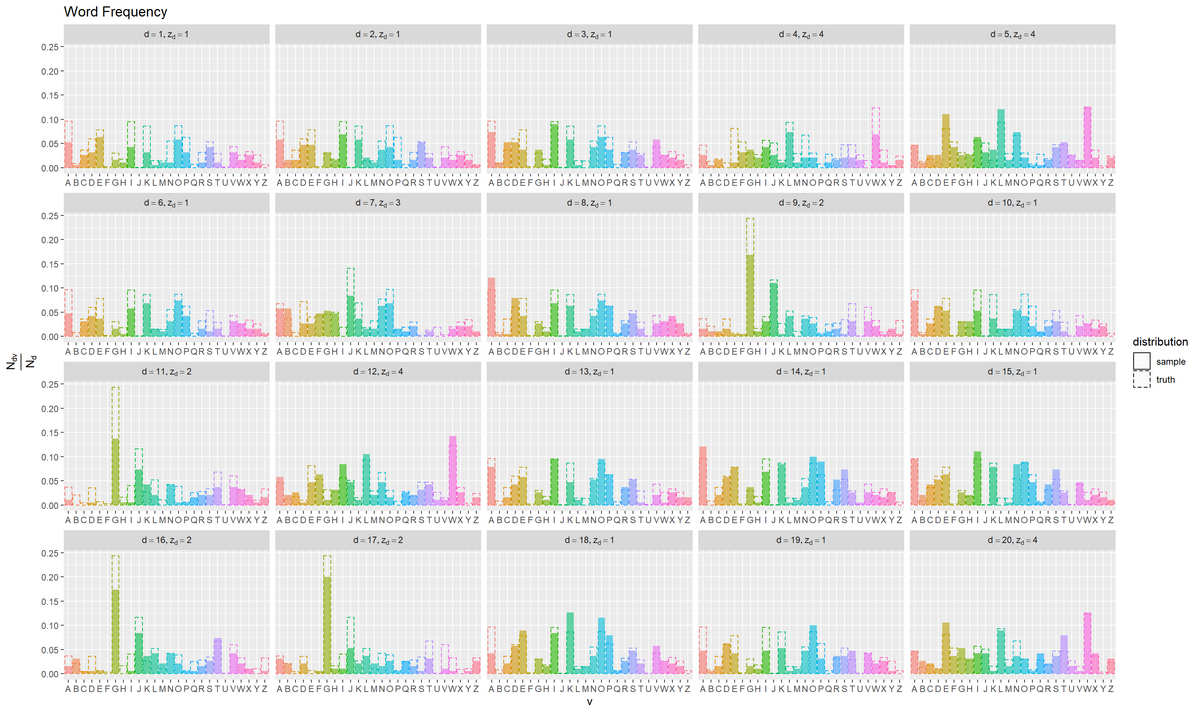
相対度数を塗りつぶし、真の出現確率を破線で示す。
x軸が語彙に対応しているのを表現するために、語彙番号ではなくアルファベットにした。
文書ごとにトピックが割り当てられており、それぞれに対応する単語分布に従って単語(語彙)が生成されているのを確認できる。
本来は、真のトピック分布と単語分布は分からないあるいは存在せず、割り当てられたトピックとトピック数も分からない。以降は、文書ごとの語彙の度数N_dvのみが手元にあるとして、トピック分布と単語分布を推定する。
推論処理
生成した文書データを用いて、トピック分布と単語分布を推定する。
パラメータの初期化
トピック数を指定して、文書数・語彙数を設定する。
# トピック数を指定 K <- 4 # 文書数と語彙数を取得 D <- nrow(N_dv) V <- ncol(N_dv) D; V
## [1] 20 ## [1] 26
トピック数$K$を指定する。
文書数$D$はN_dvの行数、語彙数$V$は列数に対応する。
各文書の単語数を作成する。
# 文書ごとの単語数を計算 N_d <- rowSums(N_dv) N_d[1:5]
## [1] 103 125 148 102 192
各文書の語彙ごとの出現回数$N_{dv}$の語彙$v$について(行ごと)の和を計算する。
負担率の受け皿を作成する。
# 負担率qの初期化 q_dk <- matrix(0, nrow = D, ncol = K) q_dk[1:5, ]
## [,1] [,2] [,3] [,4] ## [1,] 0 0 0 0 ## [2,] 0 0 0 0 ## [3,] 0 0 0 0 ## [4,] 0 0 0 0 ## [5,] 0 0 0 0
全ての値を0とするD行K列のマトリクスを$\mathbf{q} = \{\mathbf{q}_1, \cdots, \mathbf{q}_D\}$、$\mathbf{q}_d = (q_{d1}, \cdots, q_{dK})$の初期値とする。
事前分布のパラメータ(ハイパーパラメータの初期値)を指定する。
# トピック分布θの事前分布のパラメータαを指定 alpha <- 1 # 単語分布Φの事前分布のパラメータβを指定 beta <- 1
トピック分布$\boldsymbol{\theta}$の事前分布(ディリクレ分布)$p(\boldsymbol{\theta} | \alpha)$のパラメータ$\alpha > 0$と、単語分布$\boldsymbol{\Phi}$の事前分布(ディリクレ分布)$p(\boldsymbol{\phi}_k | \beta)$のパラメータ$\beta > 0$を指定する。それぞれ、次ステップの変分事後分布のパラメータの初期値として使用する。
トピック分布の変分事後分布のパラメータの初期値を作成する。
# トピック分布θの変分事後分布のパラメータαの初期化 alpha_k <- runif(n = K, min = 0.01, max = 2) # 範囲を指定 alpha_k
## [1] 0.4038141 1.9503820 1.5897569 0.3514464
K個の一様乱数をrunif()で生成し、$\boldsymbol{\theta}$の変分事後分布(ディリクレ分布)$q(\boldsymbol{\theta} | \boldsymbol{\alpha})$のパラメータ$\boldsymbol{\alpha} = (\alpha_1, \cdots, \alpha_K)$、$\alpha_k > 0$とする。
初期値によるトピック分布の期待値(変分事後分布の期待値)を計算する。
# トピック分布の期待値を計算:式(1.15) E_theta_k <- alpha_k / sum(alpha_k) E_theta_k
## [1] 0.09401084 0.45406302 0.37010688 0.08181926
ディリクレ分布の期待値は、次の式で計算できる。
$\alpha_k > 0$を総和で割っているので、$0 \leq \mathbb{E}[\theta_k] \leq 1$、$\sum_{k=1}^K \mathbb{E}[\theta_k] = 1$となり、カテゴリ分布のパラメータの条件を満たす。
「真の分布の設定」のときと同様にして、初期値によるトピック分布の期待値をグラフで確認する。
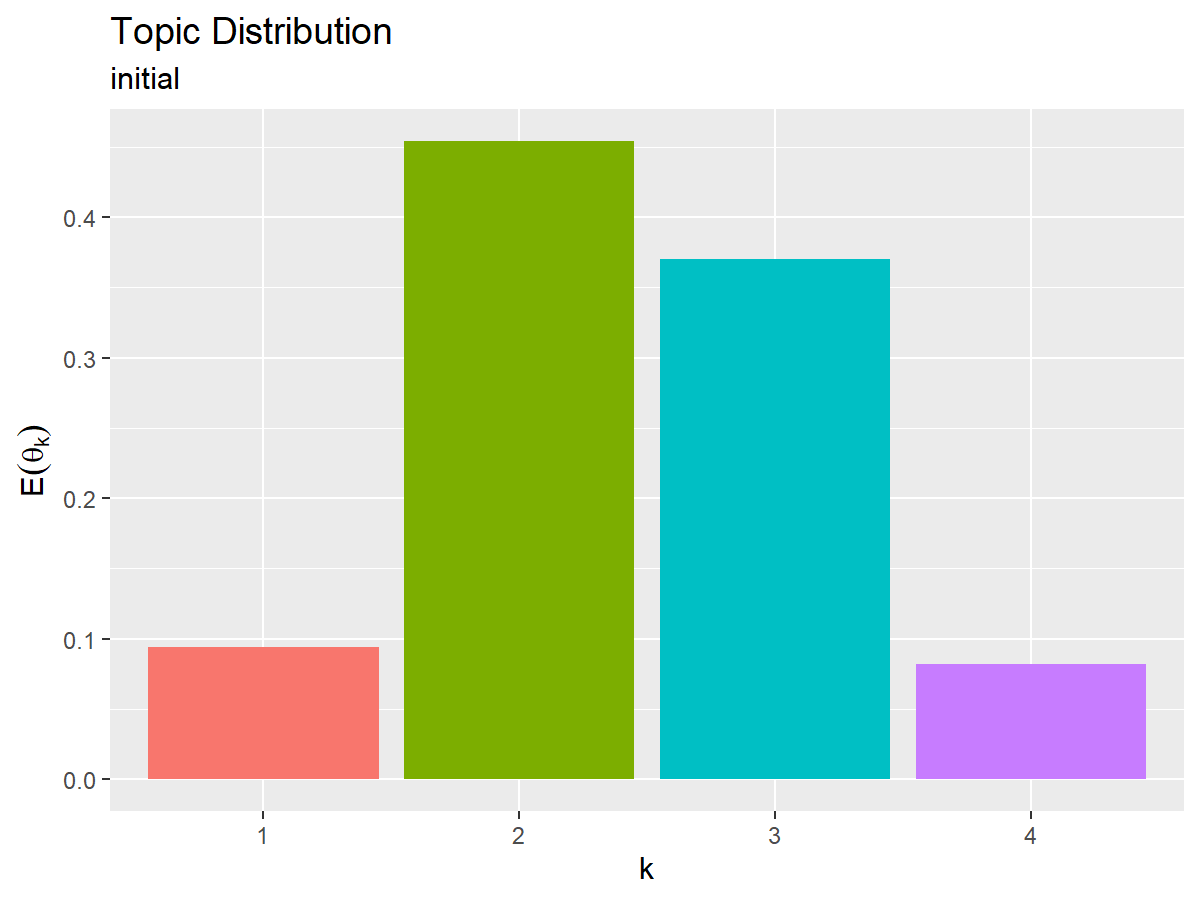
同様に、単語分布の変分事後分布のパラメータの初期値を作成する。
# 単語分布Φの変分事後分布のパラメータβの初期化 beta_kv <- runif(n = K*V, min = 0.01, max = 2) |> # 範囲を指定 matrix(nrow = K, ncol = V) beta_kv[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.3965553 1.2282330 1.841607 0.5621508 0.06196082 ## [2,] 1.2081830 1.6375765 1.053267 1.1189383 0.36672755 ## [3,] 0.3204410 0.5564344 1.812238 1.2283205 1.30676547 ## [4,] 1.0878896 1.2344523 1.877299 0.1252691 0.69281925
K×V個の一様乱数を生成してK行V列のマトリクスに整形し、K個の$\boldsymbol{\phi}_k$の変分事後分布(ディリクレ分布)$q(\boldsymbol{\phi}_k | \boldsymbol{\beta}_k)$のパラメータ$\boldsymbol{\beta} = \{\boldsymbol{\beta}_1, \cdots, \boldsymbol{\beta}_K\}$、$\boldsymbol{\beta}_k = (\beta_{k1}, \cdots, \beta_{kV})$、$\beta_{kv} > 0$とする。
初期値による単語分布の期待値(変分事後分布の期待値)を計算する。
# 単語分布の期待値を計算:式(1.15) E_phi_kv <- beta_kv / rowSums(beta_kv) E_phi_kv[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.01299578 0.04025124 0.06035252 0.018422616 0.002030559 ## [2,] 0.04438780 0.06016342 0.03869631 0.041109017 0.013473315 ## [3,] 0.01208100 0.02097823 0.06832352 0.046309124 0.049266594 ## [4,] 0.03361462 0.03814325 0.05800651 0.003870679 0.021407370
トピック分布のときと同様にして、トピック$k$(行)ごとに$\mathbb{E}[\phi_{kv}] = \frac{\beta_{kv}}{\sum_{v=1}^V \beta_{kv'}}$を計算する。
初期値による単語分布の期待値をグラフで確認する。
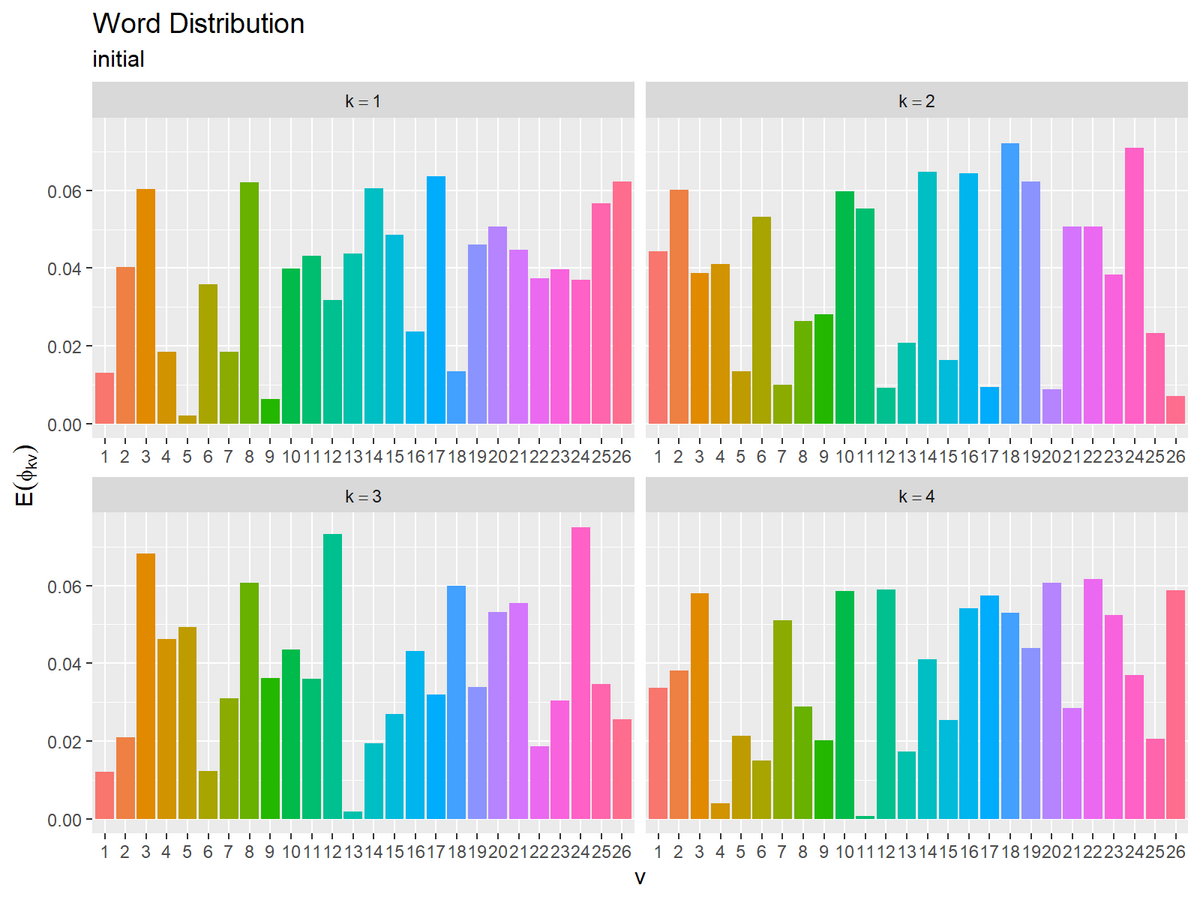
最尤推定では、トピック分布$\boldsymbol{\theta}$と単語分布$\boldsymbol{\Phi}$をそれぞれ点推定した。変分ベイズ推定では、ハイパーパラメータ$\boldsymbol{\alpha}, \boldsymbol{\beta}$を求めることで、$\boldsymbol{\theta}, \boldsymbol{\Phi}$を分布推定する。上の2つのグラフは、それぞれ推定した分布の期待値を可視化したものである。
ここまでで、推論処理の準備ができた。続いて、推論処理を行う。
コード全体
試行回数を指定して、トピック分布と単語分布の更新を繰り返す。
# 試行回数を指定 MaxIter <- 20 # 推移の確認用の受け皿を作成 trace_q_dki <- array(NA, dim = c(D, K, MaxIter)) trace_alpha_ki <- matrix(NA, nrow = K, ncol = MaxIter+1) trace_beta_kvi <- array(NA, dim = c(K, V, MaxIter+1)) # 初期値を保存 trace_alpha_ki[, 1] <- alpha_k trace_beta_kvi[, , 1] <- beta_kv # 変分ベイズ推定 for(i in 1:MaxIter) { # 次ステップのハイパーパラメータの初期化 new_alpha_k <- rep(alpha, times = K) new_beta_kv <- matrix(beta, nrow = K, ncol = V) for(d in 1:D){ ## (各文書) for(k in 1:K){ ## (各トピック) # 負担率qの計算:式(3.22) term_alpha_k <- digamma(alpha_k) - digamma(sum(alpha_k)) term_beta_k <- colSums(N_dv[d, ] * digamma(t(beta_kv))) - N_d[d] * digamma(rowSums(beta_kv)) log_q_k <- term_alpha_k + term_beta_k log_q_k <- log_q_k - min(log_q_k) # アンダーフロー対策 log_q_k <- log_q_k - max(log_q_k) # オーバーフロー対策 q_dk[d, k] <- exp(log_q_k[k]) / sum(exp(log_q_k)) # 正規化 # トピック分布θの変分事後分布のパラメータαの計算:式(3.19') new_alpha_k[k] <- new_alpha_k[k] + q_dk[d, k] for(v in 1:V){ ## (各語彙) # 単語分布Φの変分事後分布のパラメータβの計算:式(3.20') new_beta_kv[k, v] <- new_beta_kv[k, v] + q_dk[d, k] * N_dv[d, v] } ## (各語彙) } ## (各トピック) } ## (各文書) # ハイパーパラメータの更新 alpha_k <- new_alpha_k beta_kv <- new_beta_kv # i回目の更新値を保存 trace_q_dki[, , i] <- q_dk trace_alpha_ki[, i+1] <- alpha_k trace_beta_kvi[, , i+1] <- beta_kv # 動作確認 message("\r", i, "/", MaxIter, appendLF = FALSE) }
推移の確認用に、負担率とトピック分布、単語分布の初期値と更新値をそれぞれtrace_***に格納していく。
コードの解説
繰り返し行う更新処理をそれぞれ確認する。
負担率の計算
先に、前ステップで更新した(または初期値の)トピック分布$\boldsymbol{\theta}$のハイパーパラメータ$\boldsymbol{\alpha}$と単語分布$\boldsymbol{\Phi}$のハイパーパラメータ$\boldsymbol{\beta}$を用いて、負担率$\mathbf{q}$を更新する。
次の処理によって、負担率を更新(計算)する。
# 負担率qの初期化 q_dk <- matrix(0, nrow = D, ncol = K) for(d in 1:D){ for(k in 1:K){ # 負担率qの計算:式(3.22) term_alpha_k <- digamma(alpha_k) - digamma(sum(alpha_k)) term_beta_k <- colSums(N_dv[d, ] * digamma(t(beta_kv))) - N_d[d] * digamma(rowSums(beta_kv)) log_q_k <- term_alpha_k + term_beta_k log_q_k <- log_q_k - min(log_q_k) # アンダーフロー対策 log_q_k <- log_q_k - max(log_q_k) # オーバーフロー対策 q_dk[d, k] <- exp(log_q_k[k]) / sum(exp(log_q_k)) # 正規化 } } q_dk[1:5, ]
## [,1] [,2] [,3] [,4] ## [1,] 5.756575e-45 1.000000e+00 1.302662e-43 1.430820e-30 ## [2,] 1.079094e-37 1.000000e+00 3.699647e-44 7.029494e-27 ## [3,] 3.117792e-50 1.000000e+00 6.684733e-67 7.744497e-45 ## [4,] 2.519057e-24 1.494613e-47 1.043156e-32 1.000000e+00 ## [5,] 1.135299e-62 1.929898e-63 2.063251e-64 1.000000e+00
負担率の各要素の更新式は、次の式である。
ここで、$\Psi(x)$はディガンマ関数で、digamma()で計算できる。
正規化前の値を$q_{dk} \propto \tilde{q}_{dk}$とおき、対数をとった(指数をとっていない)$\log \tilde{q}_{dk}$を計算する。
$\log \tilde{q}_{dk}\ (k = 1, \dots, K)$をlog_q_kとする。
$\beta_{kv}$に関する2つの項(term_beta_k)の計算について、1つのトピックに関する次の計算を、K個同時に処理している。
# トピックkに関する計算 term_beta_k[k] <- sum(N_dv[d, ] * digamma(beta_kv[k, ])) - N_d[d] * digamma(sum(beta_kv[k, ]))
ベクトルはマトリクスの各列に対してブロードキャストして計算されるので、転置t()して要素を対応させる必要がある。また、マトリクスの形状に応じて、行ごとの和rowSums()や列ごとの和colSums()で$\sum_v$の計算を行う。
log_q_kの各要素から、最小値を引くことでアンダーフロー、最大値を引くことでオーバーフローを起きにくくする。アンダーフロー対策については「ソフトマックス関数のオーバーフロー対策【ゼロつく1のノート(数学)】 - からっぽのしょこ」を参照のこと。
K個(全てのトピック)についての和で割って正規化する。
文書番号dとトピック番号kに関するfor()によって、q_dkのD×K個の要素を1回ずつ更新する。
トピック分布と単語分布の計算
次に、更新した負担率$\mathbf{q}$を用いて、トピック分布$\boldsymbol{\theta}$のハイパーパラメータ$\boldsymbol{\alpha}$と単語分布$\boldsymbol{\Phi}$のハイパーパラメータ$\boldsymbol{\beta}$を更新する。
次の処理によって、トピック分布のハイパーパラメータを更新する。
# 次ステップのハイパーパラメータの初期化 new_alpha_k <- rep(alpha, times = K) for(d in 1:D) { for(k in 1:K) { # トピック分布θの変分事後分布のパラメータαの計算:式(3.19') new_alpha_k[k] <- new_alpha_k[k] + q_dk[d, k] } } # ハイパーパラメータの更新 res_alpha_k <- new_alpha_k res_alpha_k
## [1] 5 12 2 5
トピック分布の変分事後分布のパラメータの各要素の更新式は、次の式である。
$\alpha_k\ (k = 1, \dots, K)$をnew_alpha_kとして、ステップごとに全ての要素を事前分布のパラメータalphaに初期化しておく。トピック番号kに関するループにより、new_alpha_kのK個の要素を計算する。
また、文書番号dに関するループにより、new_alpha_k[k]にq_dk[, k]のD個の値を順番に足すことで、$\sum_d$の計算を行う。
全ての要素を計算できたら、ハイパーパラメータの値を上書きする。(次にやる作図処理に影響しないように変数名をres_***にしている。)
続いて、次の処理によって、単語分布のハイパーパラメータを更新する。
# 次ステップのハイパーパラメータの初期化 new_beta_kv <- matrix(beta, nrow = K, ncol = V) for(d in 1:D) { for(k in 1:K) { for(v in 1:V){ # 単語分布Φの変分事後分布のパラメータβの計算:式(3.20') new_beta_kv[k, v] <- new_beta_kv[k, v] + q_dk[d, k] * N_dv[d, v] } } } # ハイパーパラメータの更新 res_beta_kv <- new_beta_kv res_beta_kv[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 15 13 4 10 3 ## [2,] 155 14 53 113 117 ## [3,] 12 12 1 6 6 ## [4,] 35 13 18 9 53
単語分布の変分事後分布のパラメータの各要素の更新式は、次の式である。
$\beta_{kv}\ (k = 1, \dots, K,\ v = 1, \dots, V)$をnew_beta_kvとして、ステップごとに全ての要素をbetaに初期化しておく。トピック番号kと語彙番号vについてのループによって、new_beta_kvのK×V個の要素を計算する。
また、文書番号dのループにより、new_beta_kv[k, v]にq_dk[, k] * N_dv[, v]のD個の値を順番に足すことで、$\sum_d$の計算を行う。
全ての要素を計算できたら、ハイパーパラメータの値を上書きする。
以上が、1ステップでの更新処理である。この処理を指定した回数繰り返し行う。
推論結果の可視化
推定したトピック分布と単語分布を可視化する。
推定した分布の確認
「パラメータの初期化」や「真の分布の設定」のときと同様にして、トピック分布の期待値(変分事後分布の期待値)を計算して、推定したトピック分布のグラフを作成する。
# トピック分布の期待値を計算:式(1.15) E_theta_k <- alpha_k / sum(alpha_k) E_theta_k
## [1] 0.20833333 0.50000000 0.08333333 0.20833333
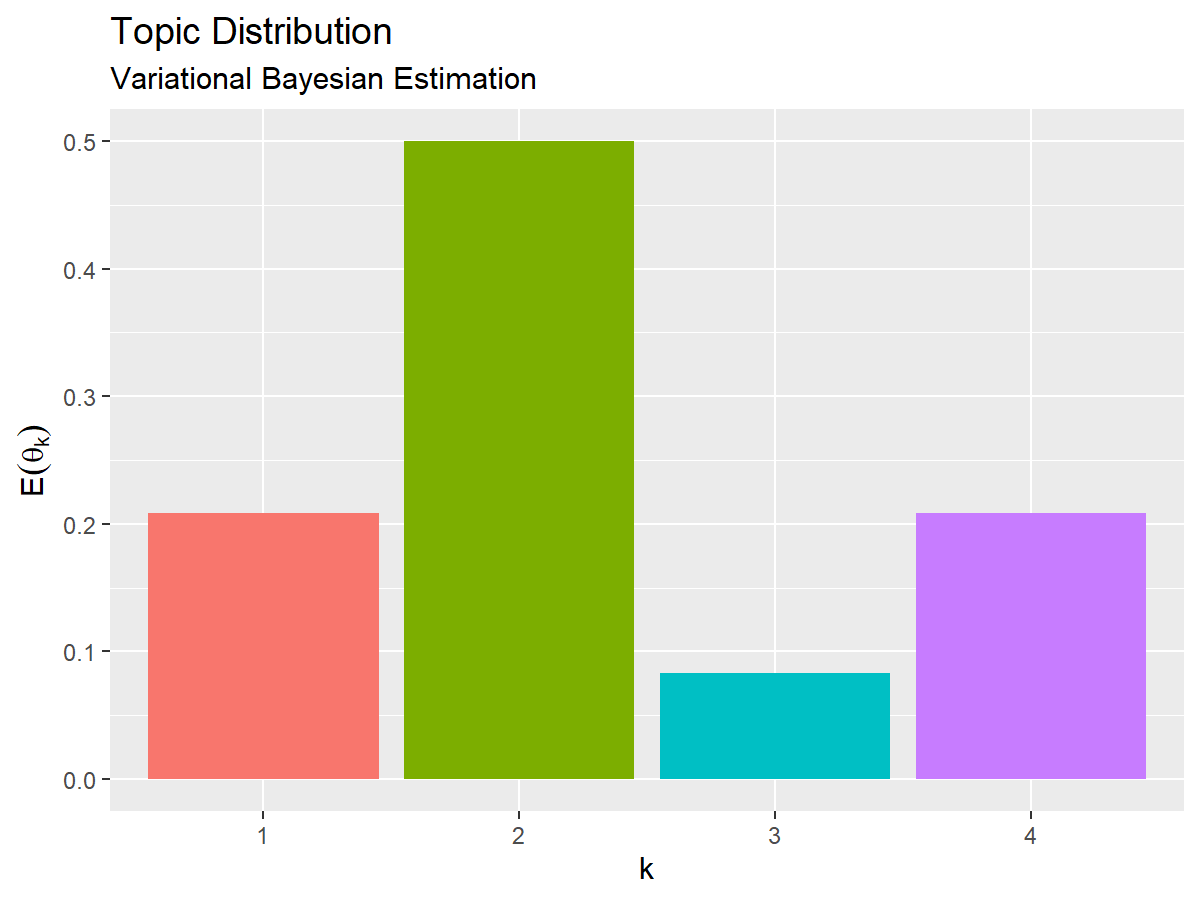
単語分布の期待値(変分事後分布の期待値)を計算して、推定した単語分布のグラフを作成する。
# 単語分布の期待値を計算:式(1.15) E_phi_kv <- beta_kv / rowSums(beta_kv) E_phi_kv[, 1:5]
## [,1] [,2] [,3] [,4] [,5] ## [1,] 0.02994012 0.025948104 0.007984032 0.01996008 0.005988024 ## [2,] 0.09433962 0.008520998 0.032258065 0.06877663 0.071211199 ## [3,] 0.07317073 0.073170732 0.006097561 0.03658537 0.036585366 ## [4,] 0.05109489 0.018978102 0.026277372 0.01313869 0.077372263
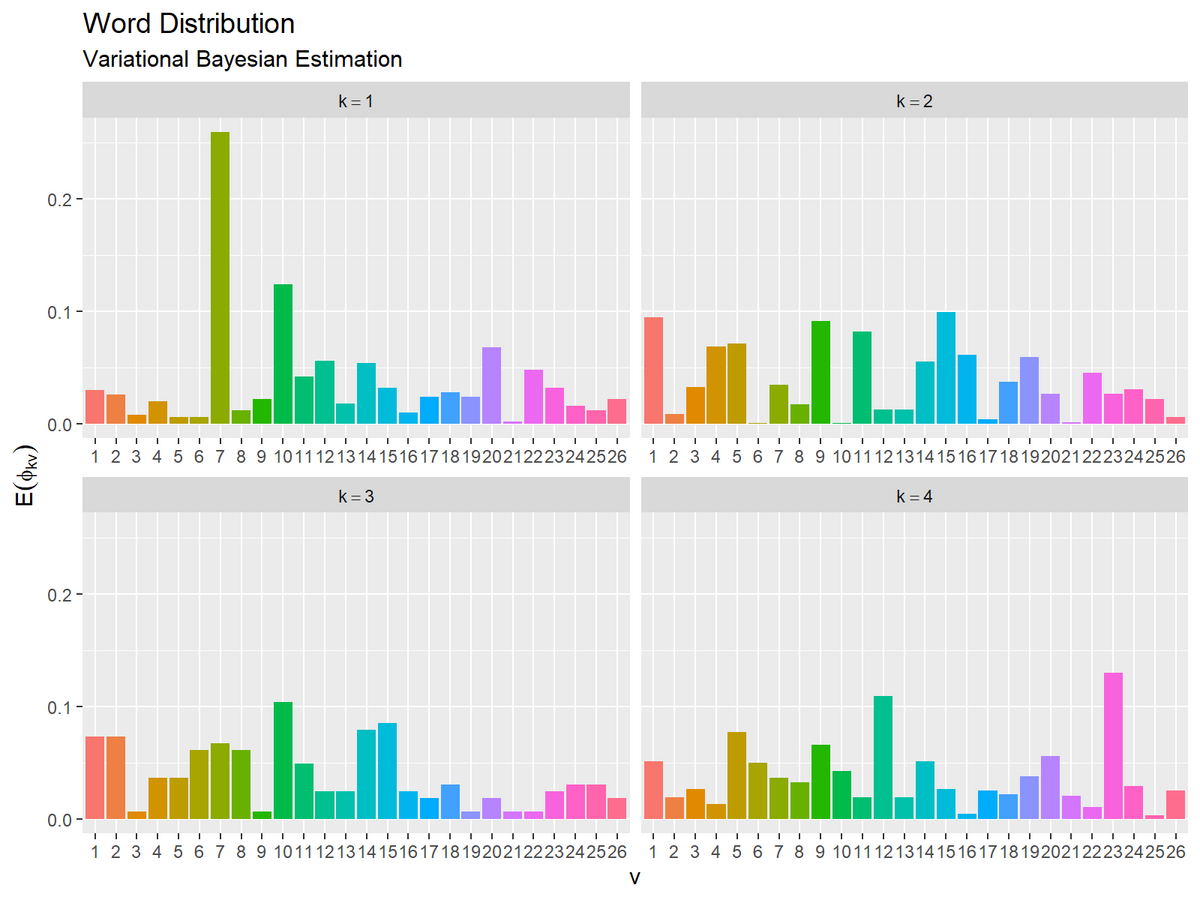
ここまでで、トピック分布と単語分布を推定できた。続いて、更新推移の様子や真の分布との対応関係を確認する。
更新推移の確認
・コード(クリックで展開)
各試行におけるトピック分布の変分事後分布のパラメータの更新値をデータフレームに格納して、試行ごとにトピックの期待値を計算する。
# 作図用のデータフレームを作成 trace_topic_df <- trace_alpha_ki |> tibble::as_tibble(.name_repair = ~as.character(0:MaxIter)) |> tibble::add_column( topic = factor(1:K) # トピック番号 ) |> tidyr::pivot_longer( cols = !topic, names_to = "iteration", # 列名を試行番号に変換 names_transform = list(iteration = as.numeric), values_to = "hyperparameter" # ハイパーパラメータ列をまとめる ) |> dplyr::group_by(iteration) |> # トピック分布の期待値計算用 dplyr::mutate( probability = hyperparameter / sum(hyperparameter) # 割り当て確率 ) |> dplyr::ungroup() |> dplyr::arrange(iteration, topic) trace_topic_df
## # A tibble: 84 × 4 ## topic iteration hyperparameter probability ## <fct> <dbl> <dbl> <dbl> ## 1 1 0 0.404 0.0940 ## 2 2 0 1.95 0.454 ## 3 3 0 1.59 0.370 ## 4 4 0 0.351 0.0818 ## 5 1 1 3.00 0.125 ## 6 2 1 12.0 0.499 ## 7 3 1 5.98 0.249 ## 8 4 1 3.04 0.127 ## 9 1 2 5.00 0.208 ## 10 2 2 12.0 0.500 ## # … with 74 more rows
K行MaxIter + 1列のマトリクスtrace_alpha_kiをデータフレームに変換して、トピック番号列を追加する。列名を0からMaxIterの整数にしておく。
試行ごとのハイパーパラメータ列を1列にまとめて、列名を試行番号に変換する。
iteration列でグループ化して、試行ごとに割り当て確率の期待値を計算する。
トピック分布のハイパーパラメータの推移の折れ線グラフを作成する。
# トピック分布のハイパーパラメータの推移を作図 ggplot() + geom_line(data = trace_topic_df, mapping = aes(x = iteration, y = hyperparameter, color = topic), alpha = 0.5, size = 1) + # 更新推移 labs(title = "Hyperparameter of the Topic Distribution", subtitle = "Variational Bayesian Estimation", x = "iteration", y = expression(alpha[k]))
トピック分布の期待値の推移のグラフを作成する。
# トピック分布の期待値の推移を作図 ggplot() + geom_line(data = trace_topic_df, mapping = aes(x = iteration, y = probability, color = topic), alpha = 0.5, size = 1) + # 更新推移 labs(title = "Topic Distribution", subtitle = "Variational Bayesian Estimation", x = "iteration", y = expression(E(theta[k])))
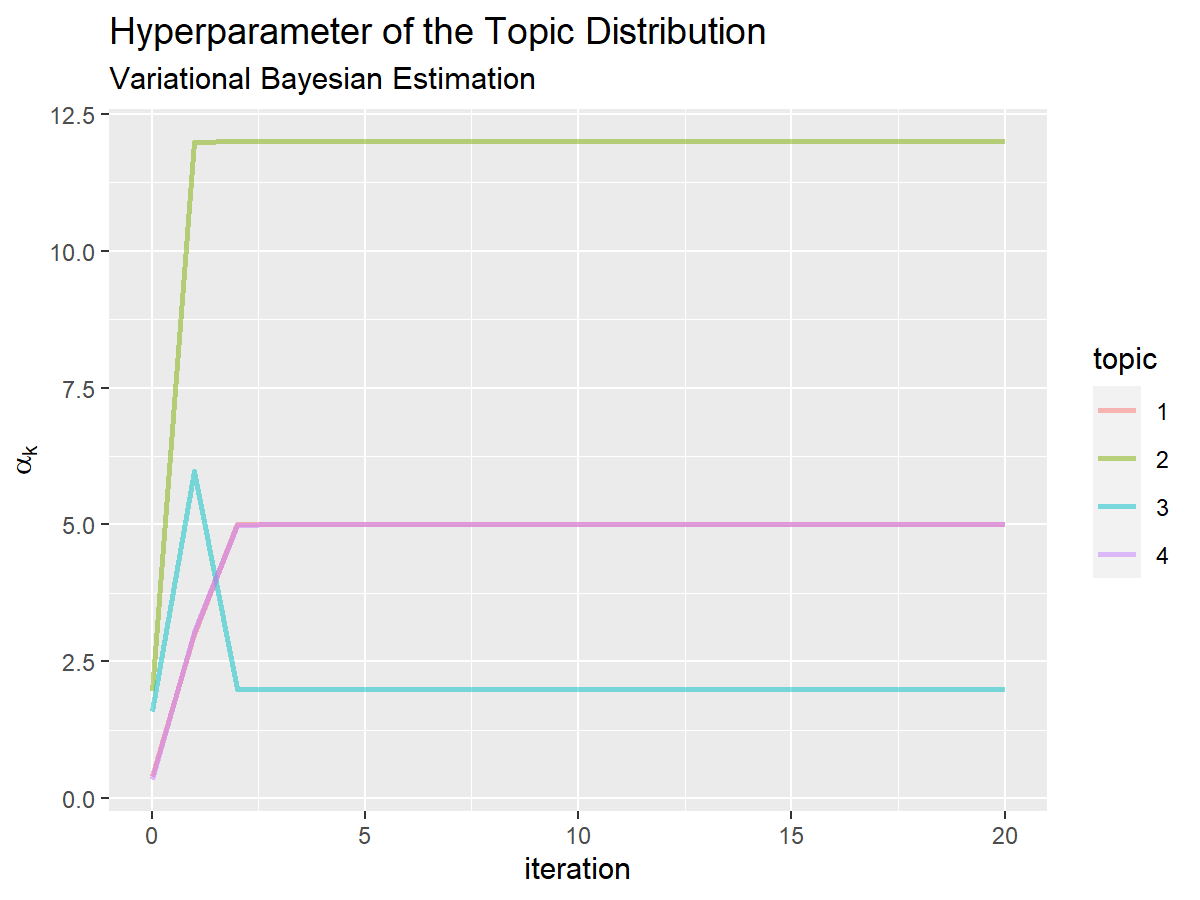
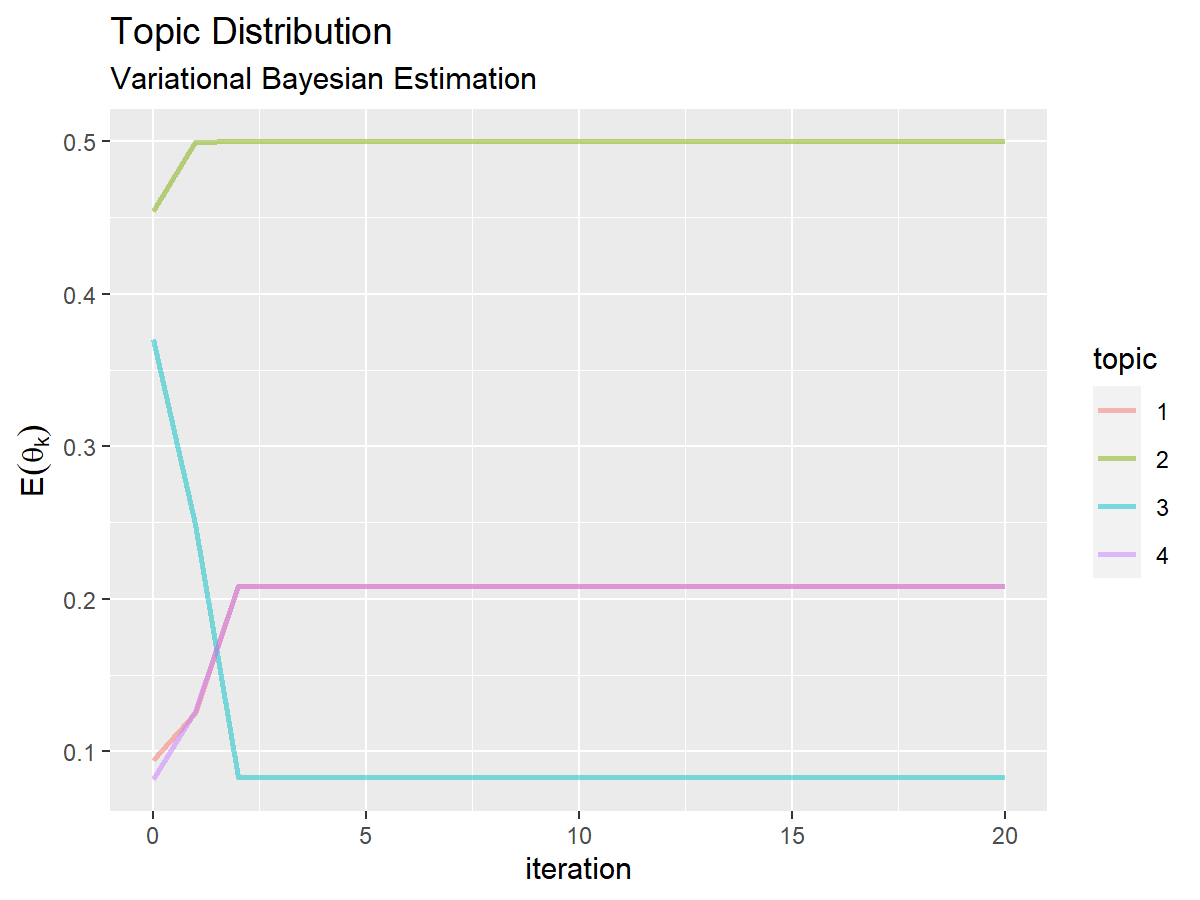
左図は、x軸を試行回数、y軸をハイパーパラメータ(hyperparameter列)として折れ線グラフを描画する。右図は、y軸を推定した確率(probability列)として折れ線グラフを描画する。
値が収束する様子を確認できる。
トピック分布のアニメーションを作成する。
・コード(クリックで展開)
# 推定トピック分布のアニメーションを作図 anime_topic_graph <- ggplot() + geom_bar(data = trace_topic_df, mapping = aes(x = topic, y = probability, fill = topic), stat = "identity", show.legend = FALSE) + # トピック分布の期待値 gganimate::transition_manual(frames = iteration) + # フレーム labs(title = "Topic Distribution", subtitle = "iteration = {current_frame}", x = "k", y = expression(E(theta[k]))) # gif画像を作成 gganimate::animate(plot = anime_topic_graph, nframes = MaxIter+1, fps = 5, width = 600, height = 450)
gganimateパッケージを利用して、アニメーション(gif画像)を作成する。
transition_manual()のフレーム制御の引数framesに試行回数列iterationを指定して、グラフを作成する。
animate()のplot引数にグラフオブジェクト、nframes引数に初期値分を加えた試行回数MaxIter + 1を指定して、gif画像を作成する。また、fps引数に1秒当たりのフレーム数を指定できる。
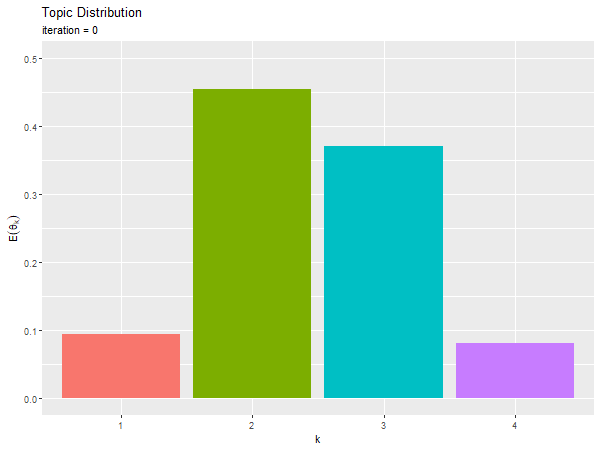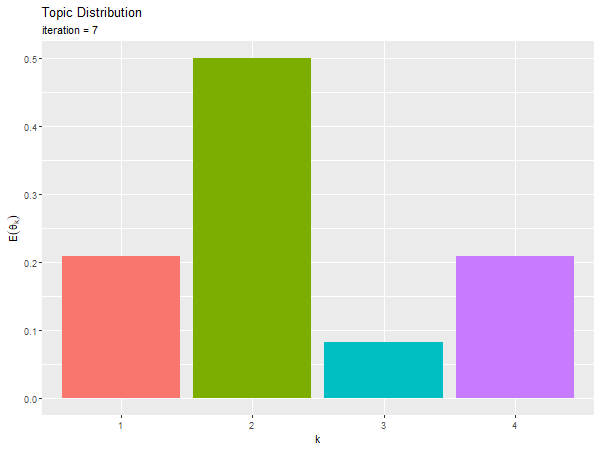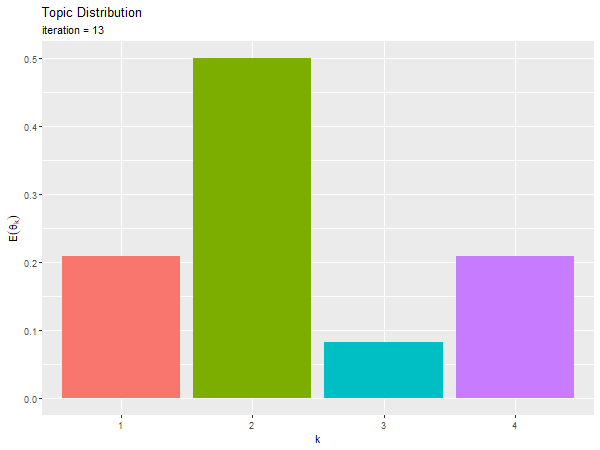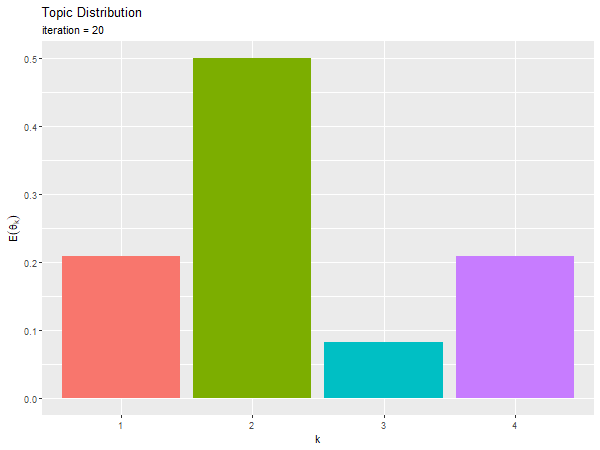
ランダムな初期値が、徐々に偏りを持つように変化するのを確認できる。
・コード(クリックで展開)
同様に、各試行における単語分布の変分事後分布のパラメータの更新値をデータフレームに格納して、試行ごとに単語分布の期待値を計算する。
# 作図用のデータフレームを作成 trace_word_df <- trace_beta_kvi |> tibble::as_tibble(.name_repair = ~as.character(1:(V*(MaxIter+1)))) |> tibble::add_column( topic = factor(1:K) # トピック番号 ) |> tidyr::pivot_longer( cols = !topic, names_to = "vi", # 列名を語彙番号×試行番号に変換 names_transform = list(vi = as.numeric), values_to = "hyperparameter" # ハイパーパラメータ列をまとめる ) |> dplyr::arrange(vi, topic) |> # 番号列の追加用 dplyr::bind_cols( tidyr::expand_grid( iteration = 0:MaxIter, # 試行番号 vocabulary = factor(1:V), # 語彙番号 tmp_topic = 1:K ) # 試行ごとに語彙番号を複製 )|> dplyr::select(!c(vi, tmp_topic)) |> # 不要な列を除去 dplyr::group_by(iteration, topic) |> # 単語分布の期待値計算用 dplyr::mutate( probability = hyperparameter / sum(hyperparameter) # 出現確率 ) |> dplyr::ungroup() |> dplyr::arrange(iteration, topic, vocabulary) trace_word_df
## # A tibble: 2,184 × 5 ## topic hyperparameter iteration vocabulary probability ## <fct> <dbl> <int> <fct> <dbl> ## 1 1 0.397 0 1 0.0130 ## 2 1 1.23 0 2 0.0403 ## 3 1 1.84 0 3 0.0604 ## 4 1 0.562 0 4 0.0184 ## 5 1 0.0620 0 5 0.00203 ## 6 1 1.09 0 6 0.0358 ## 7 1 0.564 0 7 0.0185 ## 8 1 1.90 0 8 0.0621 ## 9 1 0.193 0 9 0.00633 ## 10 1 1.21 0 10 0.0398 ## # … with 2,174 more rows
K行V列のマトリクスをMaxIter + 1個分並べた3次元配列trace_beta_kviをデータフレームに変換すると、trace_beta_kvi[, , 1]の隣の列にtrace_beta_kvi[, , 2]のように並べたデータフレームになる。
トピック番号を追加して、試行と語彙ごとのハイパーパラメータ列を1列にまとめて、試行番号と語彙番号を追加する。
iteration列でグループ化して、試行ごとに出現確率確率の期待値を計算する。
単語分布の更新値のハイパーパラメータの推移のグラフを作成する。
# 単語分布のハイパーパラメータの推移を作図 ggplot() + geom_line(data = trace_word_df, mapping = aes(x = iteration, y = hyperparameter, color = vocabulary), alpha = 0.5, size = 1) + # 更新推移 facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic)), scales = "free_y") + # 分割 labs(title = "Hyperparameter of the Word Distribution", subtitle = "Variational Bayesian Estimation", color = "v", x = "iteration", y = expression(beta[kv]))
単語分布の期待値の推移のグラフを作成する。
# 単語分布の期待値の推移を作図 ggplot() + geom_line(data = trace_word_df, mapping = aes(x = iteration, y = probability, color = vocabulary), alpha = 0.5, size = 1) + # 更新推移 facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic))) + # 分割 labs(title = "Word Distribution", subtitle = "Variational Bayesian Estimation", color = "v", x = "iteration", y = expression(E(phi[kv])))
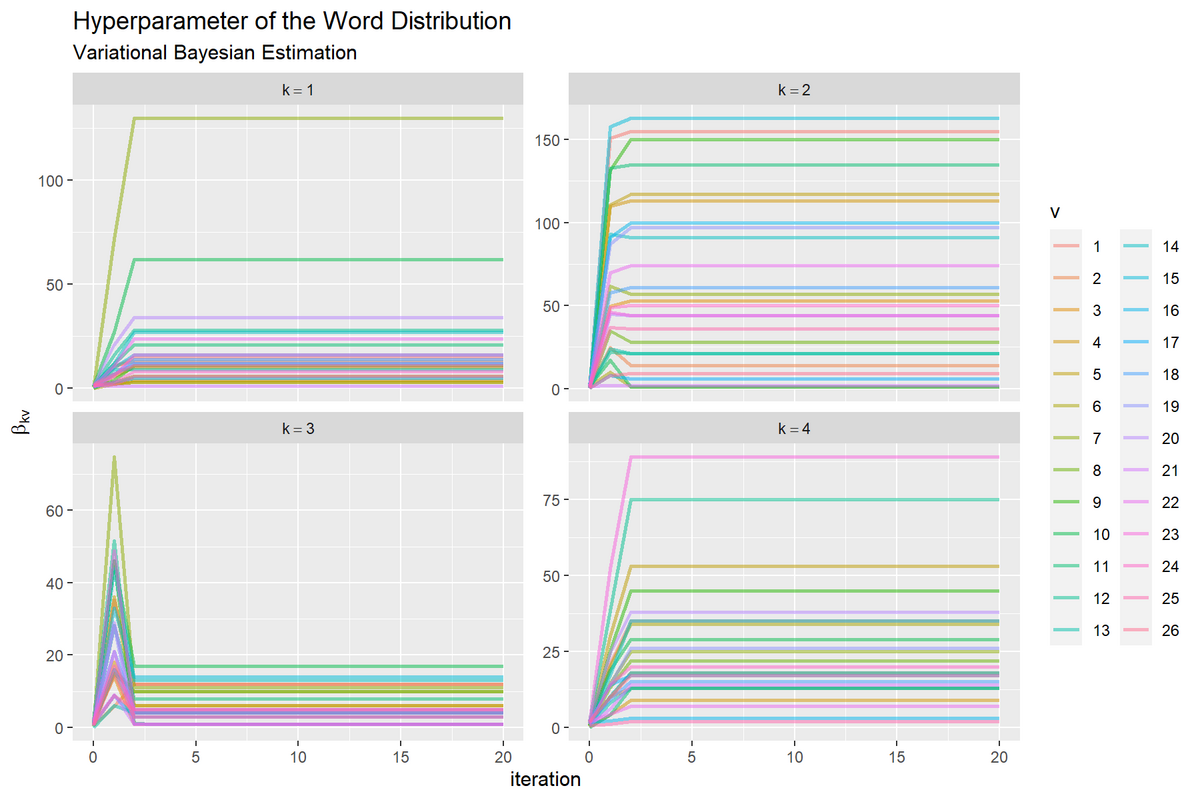
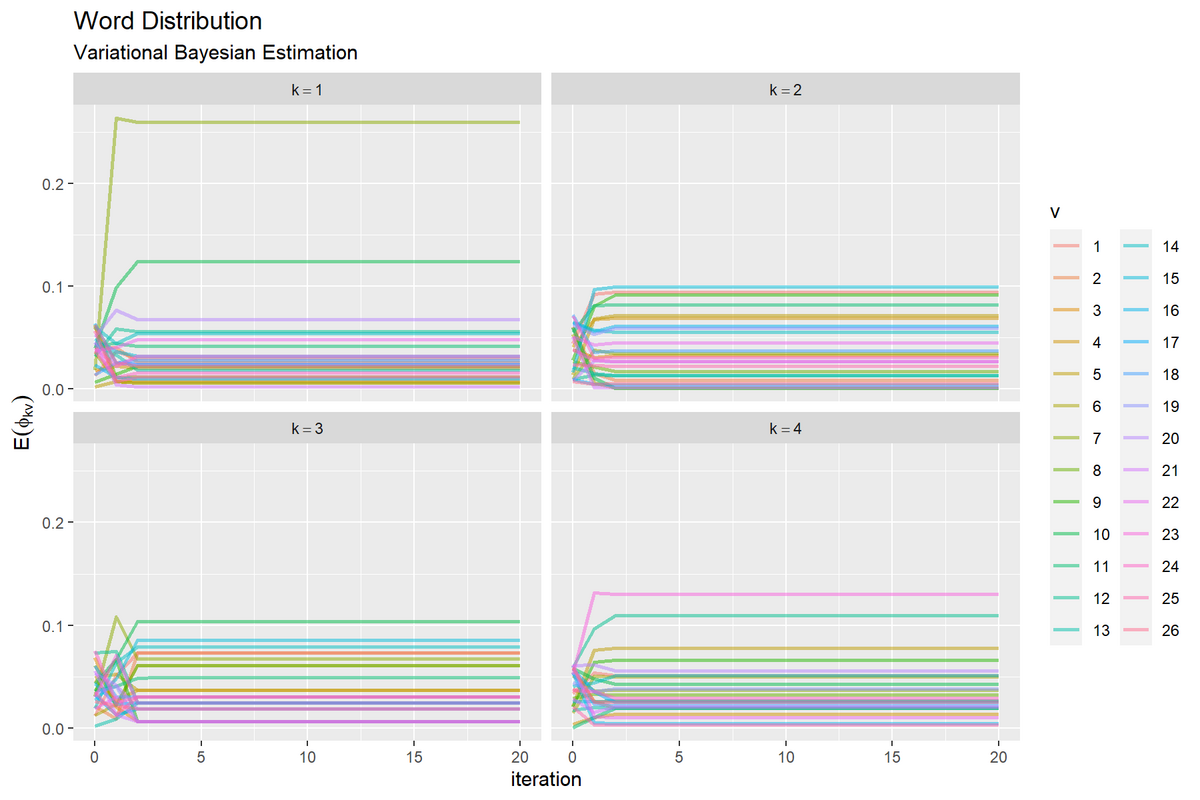
左図は、トピックごとにグラフを分割して、x軸を試行回数、y軸をハイパーパラメータ(hyperparameter列)として折れ線グラフを描画する。右図は、y軸を推定した確率(probability列)として折れ線グラフを描画する。
単語分布のアニメーションを作成する。
・コード(クリックで展開)
# 推定単語分布のアニメーションを作図 anime_word_graph <- ggplot() + geom_bar(data = trace_word_df, mapping = aes(x = vocabulary, y = probability, fill = vocabulary), stat = "identity", show.legend = FALSE) + # 単語分布の期待値 gganimate::transition_manual(frames = iteration) + # フレーム facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic)), scales = "free_x") + # 分割 labs(title = "Word Distribution", subtitle = "iteration = {current_frame}", x = "v", y = expression(E(phi[kv]))) # gif画像を作成 gganimate::animate(plot = anime_word_graph, nframes = MaxIter+1, fps = 5, width = 800, height = 600)
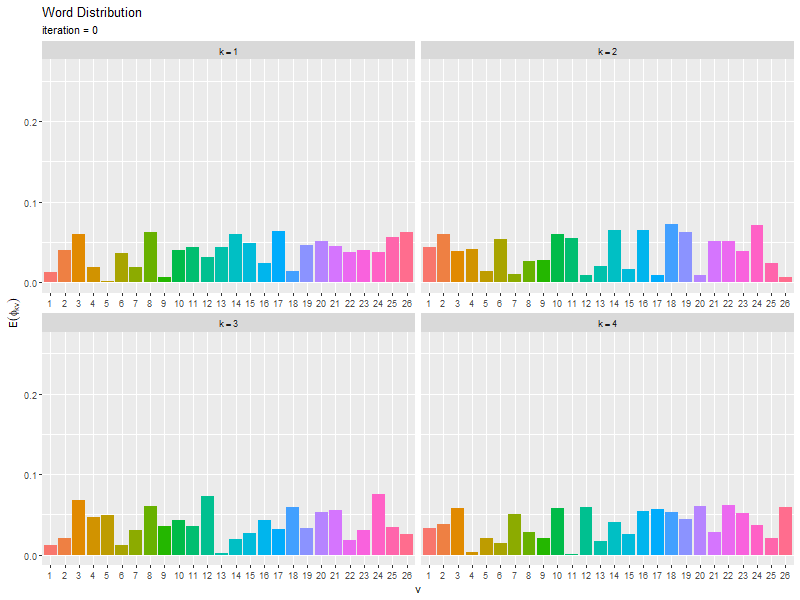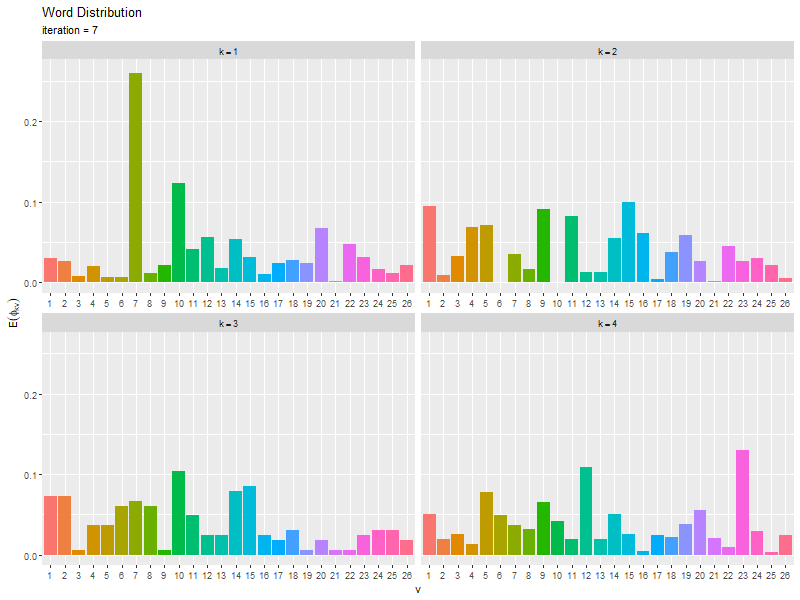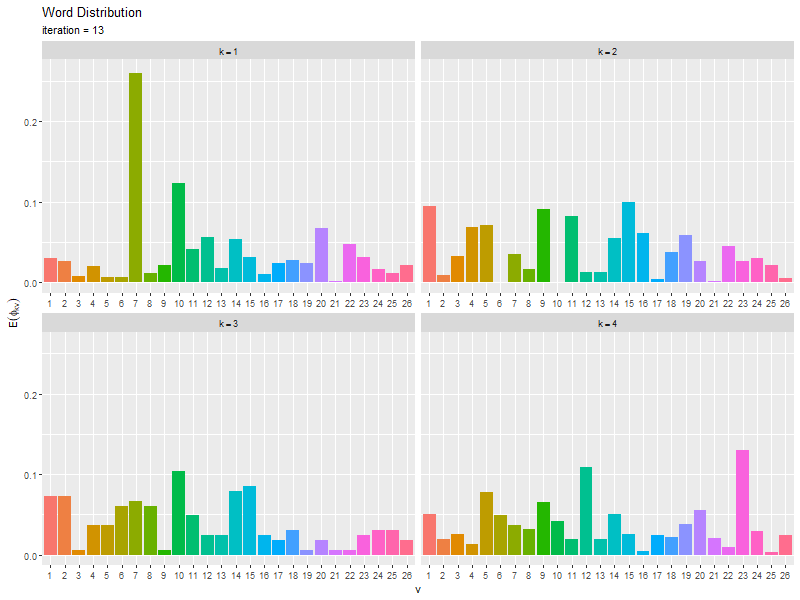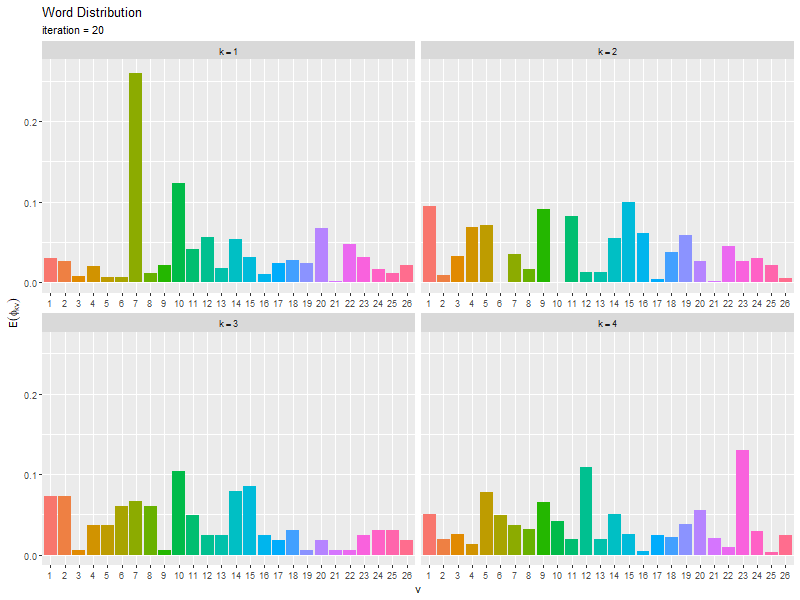
・コード(クリックで展開)
負担率の更新値をデータフレームに格納する。
# 作図用のデータフレームを作成 trace_response_df <- trace_q_dki |> tibble::as_tibble(.name_repair = ~as.character(1:(K*MaxIter))) |> tibble::add_column( document = factor(1:D) # 文書番号 ) |> tidyr::pivot_longer( cols = !document, names_to = "ki", # 列名を語彙番号×試行番号に変換 names_transform = list(ki = as.numeric), values_to = "responsibility" # 負担率列をまとめる ) |> dplyr::arrange(ki, document) |> # 番号列の追加用 dplyr::bind_cols( tidyr::expand_grid( iteration = 1:MaxIter, # 試行番号 topic = factor(1:K), # トピック番号 tmp_document = 1:D ) # 試行ごとにトピック番号を複製 )|> dplyr::select(!c(ki, tmp_document)) |> # 不要な列を除去 dplyr::arrange(iteration, document, topic) trace_response_df
## # A tibble: 1,600 × 4 ## document responsibility iteration topic ## <fct> <dbl> <int> <fct> ## 1 1 1.77e- 92 1 1 ## 2 1 1.00e+ 0 1 2 ## 3 1 5.24e- 11 1 3 ## 4 1 7.96e-123 1 4 ## 5 2 2.58e- 76 1 1 ## 6 2 1.00e+ 0 1 2 ## 7 2 1.37e- 6 1 3 ## 8 2 2.82e-222 1 4 ## 9 3 3.44e- 83 1 1 ## 10 3 9.80e- 1 1 2 ## # … with 1,590 more rows
D行K列のマトリクスをMaxIter個分並べた3次元配列trace_q_dkiをデータフレームに変換して、トピック番号を追加する。
試行と語彙ごとのハイパーパラメータ列を1列にまとめて、試行番号と語彙番号を追加する。
負担率の推移の折れ線グラフを作成する。
# 負担率の推移を作図 ggplot() + geom_line(data = trace_response_df, mapping = aes(x = iteration, y = responsibility, color = topic), alpha = 0.5, size = 1) + # 更新推移 facet_wrap(document ~ ., labeller = label_bquote(d==.(document))) + # 分割 labs(title = "responsibility", subtitle = "Variational Bayesian Estimation", color = "k", x = "iteration", y = expression(q[dk]))
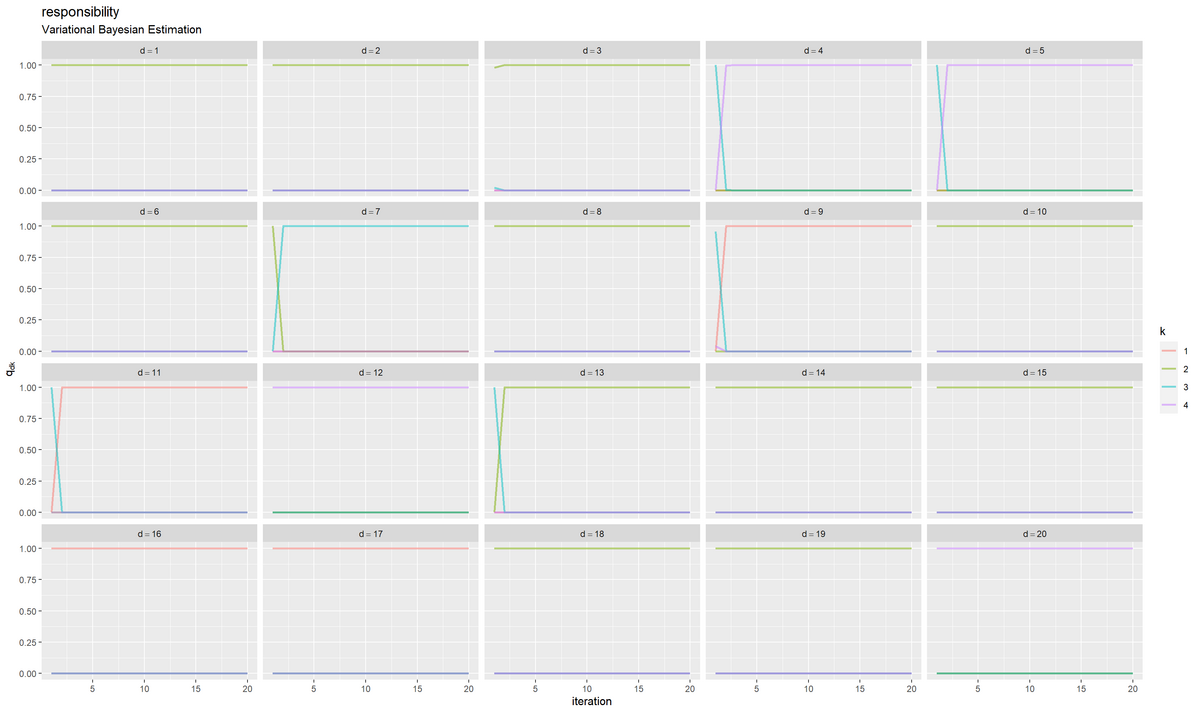
文書ごとにグラフを分割して、x軸を試行回数、y軸を負担率(responsibility列)として折れ線グラフを描画する。
負担率は、各文書の推定トピックを確率で表している。更新を繰り返すことで、それぞれ1つのトピックに収束しているのが分かる。
真の分布との比較
最後に、文書データの生成モデル(真の分布)と推定した分布との対応関係を考える。詳しくは「[KL情報量が最小となるように確率分布の次元を入れ替えたい - からっぽのしょこ」を参照のこと。
・コード(クリックで展開)
真の分布と推定した分布のKL情報量を計算する。
# インデックスの組み合わせを作成してKL情報量を計算 kl_df <- tidyr::expand_grid( group = 1:gamma(K+1), # 組み合わせ番号 k = factor(1:K) # 真の分布・並べ替え後のトピック番号 ) |> # トピック番号を複製 tibble::add_column( j = gtools::permutations(n = K, r = K, v = 1:K) |> # トピック番号の順列を作成 t() |> as.vector() |> factor() # 元のトピック番号・並べ替え用のインデックス ) |> dplyr::group_by(group) |> # 組み合わせごとの計算用 dplyr::mutate( # KL情報量を計算 kl_topic = sum(theta_true_k * (log(theta_true_k) - log(E_theta_k[j]))), # トピック分布のKL情報量 kl_word = sum(phi_true_kv * (log(phi_true_kv) - log(E_phi_kv[j, ]))), # 単語分布のKL情報量 kl_sum = kl_topic + kl_word/V ) |> dplyr::ungroup() |> dplyr::arrange(kl_sum, group, k) # 当て嵌まりが良い順に並べ替え kl_df
## # A tibble: 96 × 6 ## group k j kl_topic kl_word kl_sum ## <int> <fct> <fct> <dbl> <dbl> <dbl> ## 1 7 1 2 0.0422 0.133 0.0473 ## 2 7 2 1 0.0422 0.133 0.0473 ## 3 7 3 3 0.0422 0.133 0.0473 ## 4 7 4 4 0.0422 0.133 0.0473 ## 5 12 1 2 0.0422 1.31 0.0925 ## 6 12 2 4 0.0422 1.31 0.0925 ## 7 12 3 3 0.0422 1.31 0.0925 ## 8 12 4 1 0.0422 1.31 0.0925 ## 9 1 1 1 0.115 2.00 0.191 ## 10 1 2 2 0.115 2.00 0.191 ## # … with 86 more rows
単語分布のKL情報量$\mathrm{KL}(\boldsymbol{\theta}^{(\mathrm{truth})}, \boldsymbol{\theta}) = \sum_{k=1}^K \theta_k^{(\mathrm{truth})} \log \frac{\theta_k^{(\mathrm{truth})}}{\theta_k}$とトピック分布のKL情報量$\mathrm{KL}(\boldsymbol{\Phi}^{(\mathrm{truth})}, \boldsymbol{\Phi}) = \sum_{k=1}^K \sum_{v=1}^V \phi_{kv}^{(\mathrm{truth})} \log \frac{\phi_{kv}^{(\mathrm{truth})}}{\phi_{kv}}$を足してkl_sum列とする。ただし単語分布に関して、$v$についての和の影響を取り除くために、$V$で割った値を足すことにする。
真の分布を推定(近似)できている組み合わせが上にくるように、KL情報量が小さい順に行を並べ替える。
KL情報量が最小になるインデックスを取り出す。
# KL情報量が最小となるトピック番号を抽出 adapt_idx <- kl_df |> dplyr::slice_head(n = K) |> # 最小の組み合わせを抽出 dplyr::pull(j) |> # 列をベクトルに変換 as.numeric() # 数値に変換 adapt_idx
## [1] 2 1 3 4
kl_dfの上からK行分のj列をベクトルとして取り出してadapt_idxとする。
・コード(クリックで展開)
推定したトピック分布のトピック番号を入れ替えてデータフレームに格納する。
# 作図用のデータフレームを作成 E_topic_df <- tibble::tibble( k = factor(adapt_idx), # 推定時のトピック番号 topic = factor(1:K), # 真の分布に対応したトピック番号 probability = E_theta_k[adapt_idx] # 割り当て確率 ) E_topic_df
## # A tibble: 4 × 3 ## k topic probability ## <fct> <fct> <dbl> ## 1 2 1 0.5 ## 2 1 2 0.208 ## 3 3 3 0.0833 ## 4 4 4 0.208
adapt_idxを使ってE_theta_kの要素を入れ替えてから、これまでと同様にして処理する。
トピック分布の期待値を真の分布に重ねてグラフを作成する。
# トピック分布を作図 ggplot() + geom_bar(data = E_topic_df, mapping = aes(x = topic, y = probability, fill = k, linetype = "result"), stat = "identity", alpha = 0.5) + # 推定トピック分布 geom_bar(data = true_topic_df, mapping = aes(x = topic, y = probability, color = topic, linetype = "truth"), stat = "identity", alpha = 0) + # 真のトピック分布 scale_linetype_manual(breaks = c("result", "truth"), values = c("solid", "dashed"), name = "distribution") + # 線の種類:(凡例表示用) guides(color = "none", fill = "none", linetype = guide_legend(override.aes = list(color = c("black", "black"), fill = c("white", "white")))) + # 凡例の体裁:(凡例表示用) labs(title = "Topic Distribution", subtitle = "Variational Bayesian Estimation", x = "k", y = expression(E(theta[k])))
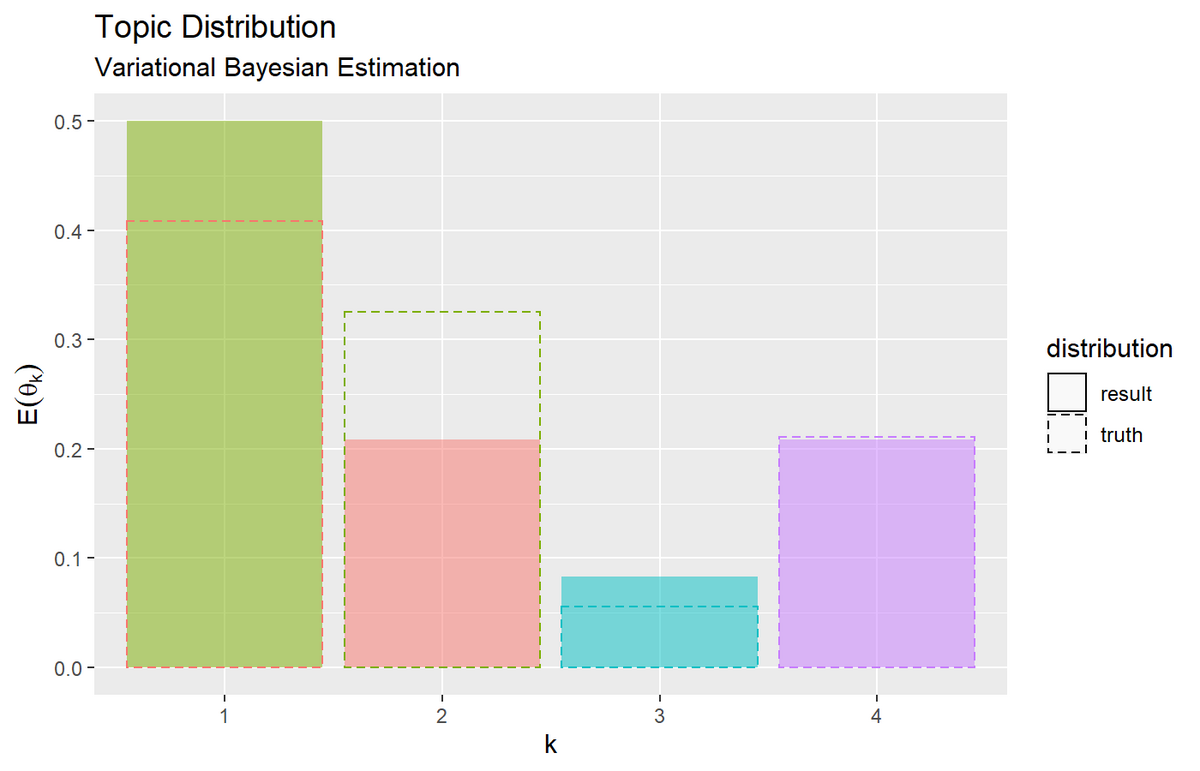
推定した分布を塗りつぶし、真の分布を破線で示す。
・コード(クリックで展開)
推定した単語分布のトピック番号を入れ替えてデータフレームに格納する。
# 作図用のデータフレームを作成 E_word_df <- E_phi_kv[adapt_idx, ] |> tibble::as_tibble(.name_repair = ~as.character(1:V)) |> tibble::add_column( k = factor(adapt_idx), # 推定時のトピック番号 topic = factor(1:K) # 真の分布に対応したトピック番号 ) |> tidyr::pivot_longer( cols = !c(k, topic), names_to = "vocabulary", # 列名を語彙番号に変換 names_ptypes = list(vocabulary = factor()), values_to = "probability" # 出現確率列をまとめる ) E_word_df
## # A tibble: 104 × 4 ## k topic vocabulary probability ## <fct> <fct> <fct> <dbl> ## 1 2 1 1 0.0943 ## 2 2 1 2 0.00852 ## 3 2 1 3 0.0323 ## 4 2 1 4 0.0688 ## 5 2 1 5 0.0712 ## 6 2 1 6 0.000609 ## 7 2 1 7 0.0347 ## 8 2 1 8 0.0170 ## 9 2 1 9 0.0913 ## 10 2 1 10 0.000609 ## # … with 94 more rows
adapt_idxを使ってphi_kvの行を入れ替えてから、これまでと同様にして処理する。
単語分布の期待値を真の分布に重ねてのグラフを作成する。
# 単語分布を作図 ggplot() + geom_bar(data = E_word_df, mapping = aes(x = vocabulary, y = probability, fill = vocabulary, linetype = "result"), stat = "identity", alpha = 0.5) + # 推定単語分布 geom_bar(data = true_word_df, mapping = aes(x = vocabulary, y = probability, color = vocabulary, linetype = "truth"), stat = "identity", alpha = 0) + # 真の単語分布 facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic)), scales = "free_x") + # 分割 scale_linetype_manual(breaks = c("result", "truth"), values = c("solid", "dashed"), name = "distribution") + # 線の種類:(凡例表示用) guides(color = "none", fill = "none", linetype = guide_legend(override.aes = list(color = c("black", "black"), fill = c("white", "white")))) + # 凡例の体裁:(凡例表示用) labs(title = "Word Distribution", subtitle = "Variational Bayesian Estimation", x = "v", y = expression(E(phi[kv])))
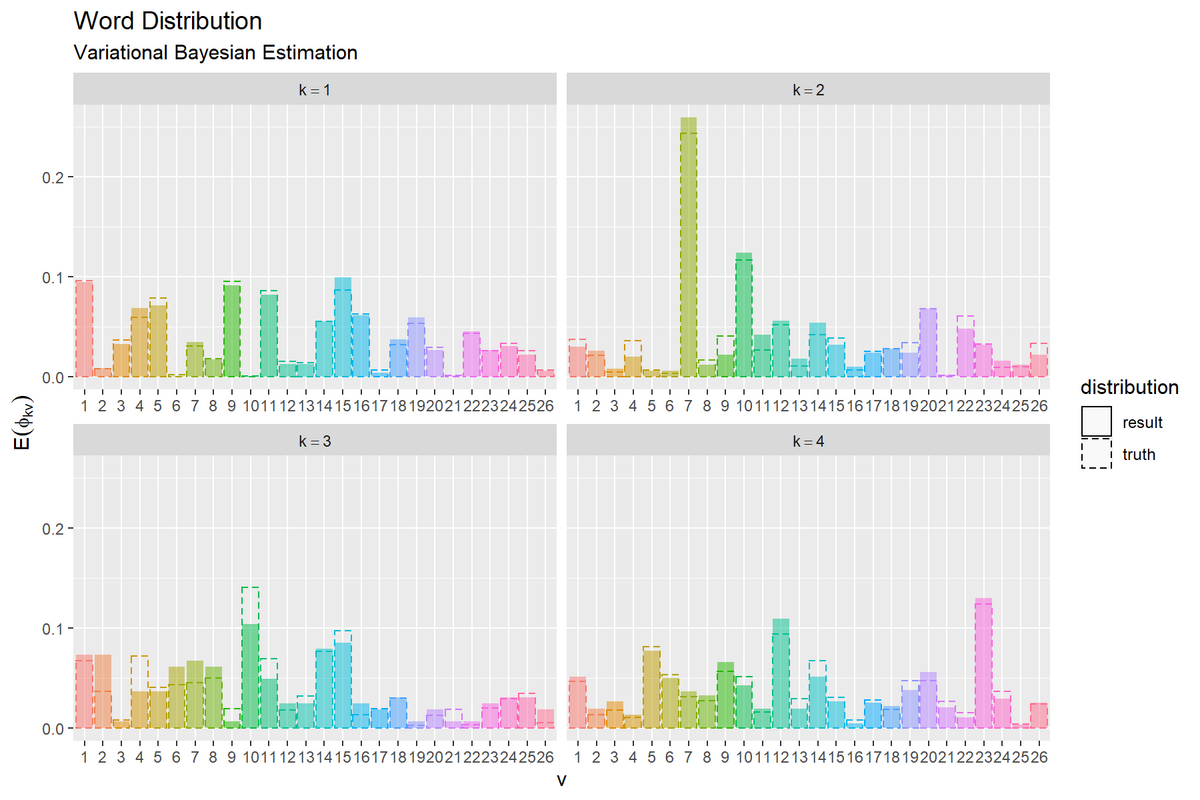
真の分布を推定(近似)できているかを確認できる。
・コード(クリックで展開)
各試行におけるトピック分布の更新値をデータフレームに格納する。
# 作図用のデータフレームを作成 trace_topic_df <- trace_alpha_ki[adapt_idx, ] |> tibble::as_tibble(.name_repair = ~as.character(0:MaxIter)) |> tibble::add_column( k = factor(adapt_idx), # 推定時のトピック番号 topic = factor(1:K) # トピック番号 ) |> tidyr::pivot_longer( cols = !c(k, topic), names_to = "iteration", # 列名を試行番号に変換 names_transform = list(iteration = as.numeric), values_to = "hyperparameter" # ハイパーパラメータ列をまとめる ) |> dplyr::group_by(iteration) |> # トピック分布の期待値計算用 dplyr::mutate( probability = hyperparameter / sum(hyperparameter) # 割り当て確率 ) |> dplyr::ungroup() |> dplyr::arrange(iteration, topic) trace_topic_df
## # A tibble: 84 × 5 ## k topic iteration hyperparameter probability ## <fct> <fct> <dbl> <dbl> <dbl> ## 1 2 1 0 1.95 0.454 ## 2 1 2 0 0.404 0.0940 ## 3 3 3 0 1.59 0.370 ## 4 4 4 0 0.351 0.0818 ## 5 2 1 1 12.0 0.499 ## 6 1 2 1 3.00 0.125 ## 7 3 3 1 5.98 0.249 ## 8 4 4 1 3.04 0.127 ## 9 2 1 2 12.0 0.500 ## 10 1 2 2 5.00 0.208 ## # … with 74 more rows
adapt_idxを使ってtrace_theta_kiの行を入れ替えてから、「更新推移の可視化」のときと同様にして処理する。
真のトピック分布をフレーム数分に複製する。
# 真のトピック分布を複製 anime_true_topic_df <- tidyr::expand_grid( iteration = 0:MaxIter, # 試行番号 true_topic_df ) anime_true_topic_df
## # A tibble: 84 × 3 ## iteration topic probability ## <int> <fct> <dbl> ## 1 0 1 0.408 ## 2 0 2 0.325 ## 3 0 3 0.0557 ## 4 0 4 0.211 ## 5 1 1 0.408 ## 6 1 2 0.325 ## 7 1 3 0.0557 ## 8 1 4 0.211 ## 9 2 1 0.408 ## 10 2 2 0.325 ## # … with 74 more rows
試行番号と真のトピック分布true_topic_dfの行の全ての組み合わせを作成することで、MaxIter + 1個に複製する。
トピック分布のアニメーションを作成する。
# トピック分布のアニメーションを作図 anime_topic_graph <- ggplot() + geom_bar(data = trace_topic_df, mapping = aes(x = topic, y = probability, fill = k, linetype = "result"), stat = "identity", alpha = 0.5) + # 推定トピック分布 geom_bar(data = anime_true_topic_df, mapping = aes(x = topic, y = probability, color = topic, linetype = "truth"), stat = "identity", alpha = 0) + # 真のトピック分布 gganimate::transition_manual(frames = iteration) + # フレーム scale_linetype_manual(breaks = c("result", "truth"), values = c("solid", "dashed"), name = "distribution") + # 線の種類:(凡例表示用) guides(color = "none", fill = "none", linetype = guide_legend(override.aes = list(color = c("black", "black"), fill = c("white", "white")))) + # 凡例の体裁:(凡例表示用) labs(title = "Topic Distribution", subtitle = "iteration = {current_frame}", x = "k", y = expression(E(theta[k]))) # gif画像を作成 gganimate::animate(plot = anime_topic_graph, nframes = MaxIter+1, fps = 5, width = 700, height = 450)
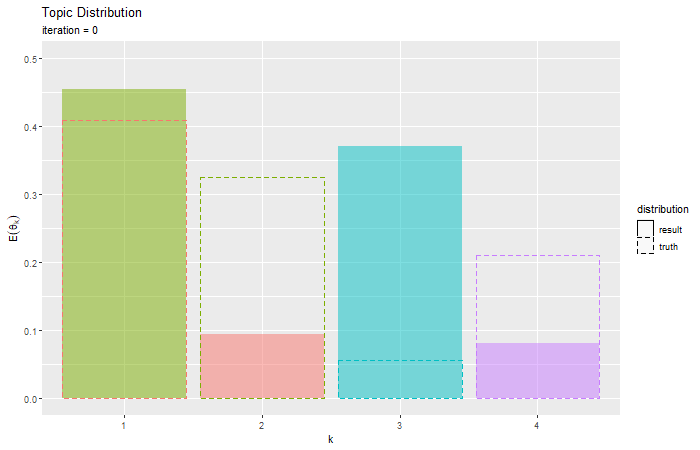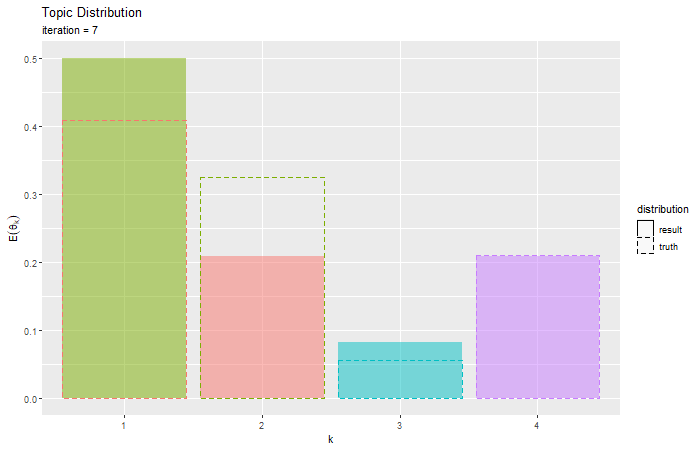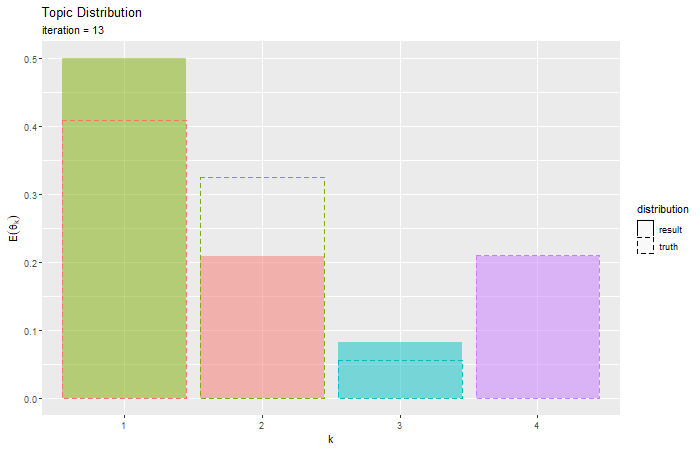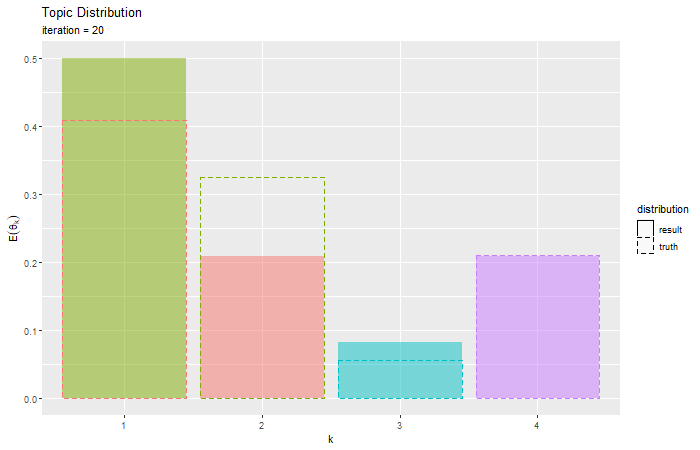
・コード(クリックで展開)
各試行における単語分布の更新値をデータフレームに格納する。
# 作図用のデータフレームを作成 trace_word_df <- trace_beta_kvi[adapt_idx, , ] |> tibble::as_tibble(.name_repair = ~as.character(1:(V*(MaxIter+1)))) |> tibble::add_column( k = factor(adapt_idx), # 推定時のトピック番号 topic = factor(1:K) # トピック番号 ) |> tidyr::pivot_longer( cols = !c(k, topic), names_to = "vi", # 列名を語彙番号×試行番号に変換 names_transform = list(vi = as.numeric), values_to = "hyperparameter" # ハイパーパラメータ列をまとめる ) |> dplyr::arrange(vi, topic) |> # 番号列の追加用 dplyr::bind_cols( tidyr::expand_grid( iteration = 0:MaxIter, # 試行番号 vocabulary = factor(1:V), # 語彙番号 tmp_topic = 1:K ) # 試行ごとに語彙番号を複製 )|> dplyr::select(!c(vi, tmp_topic)) |> # 不要な列を除去 dplyr::group_by(iteration, topic) |> # 単語分布の期待値計算用 dplyr::mutate( probability = hyperparameter / sum(hyperparameter) # 出現確率 ) |> dplyr::ungroup() |> dplyr::arrange(iteration, topic, vocabulary) trace_word_df
## # A tibble: 2,184 × 6 ## k topic hyperparameter iteration vocabulary probability ## <fct> <fct> <dbl> <int> <fct> <dbl> ## 1 2 1 1.21 0 1 0.0444 ## 2 2 1 1.64 0 2 0.0602 ## 3 2 1 1.05 0 3 0.0387 ## 4 2 1 1.12 0 4 0.0411 ## 5 2 1 0.367 0 5 0.0135 ## 6 2 1 1.45 0 6 0.0532 ## 7 2 1 0.269 0 7 0.00989 ## 8 2 1 0.718 0 8 0.0264 ## 9 2 1 0.766 0 9 0.0281 ## 10 2 1 1.63 0 10 0.0597 ## # … with 2,174 more rows
adapt_idxを使ってtrace_phi_kviの行を入れ替えてから、「更新推移の可視化」のときと同様にして処理する。
真の単語分布をフレーム数分に複製する。
# 真の単語分布を複製 anime_true_word_df <- tidyr::expand_grid( iteration = 0:MaxIter, # 試行番号 true_word_df ) anime_true_word_df
## # A tibble: 2,184 × 4 ## iteration topic vocabulary probability ## <int> <fct> <fct> <dbl> ## 1 0 1 1 0.0960 ## 2 0 1 2 0.00805 ## 3 0 1 3 0.0362 ## 4 0 1 4 0.0595 ## 5 0 1 5 0.0782 ## 6 0 1 6 0.00207 ## 7 0 1 7 0.0303 ## 8 0 1 8 0.0177 ## 9 0 1 9 0.0953 ## 10 0 1 10 0.000692 ## # … with 2,174 more rows
単語分布のアニメーションを作成する。
# 単語分布のアニメーションを作図 anime_word_graph <- ggplot() + geom_bar(data = trace_word_df, mapping = aes(x = vocabulary, y = probability, fill = vocabulary, linetype = "result"), stat = "identity", alpha = 0.5) + # 推定単語分布 geom_bar(data = anime_true_word_df, mapping = aes(x = vocabulary, y = probability, color = vocabulary, linetype = "truth"), stat = "identity", alpha = 0) + # 真の単語分布 gganimate::transition_manual(frames = iteration) + # フレーム facet_wrap(topic ~ ., labeller = label_bquote(k==.(topic)), scales = "free_x") + # 分割 scale_linetype_manual(breaks = c("result", "truth"), values = c("solid", "dashed"), name = "distribution") + # 線の種類:(凡例表示用) guides(color = "none", fill = "none", linetype = guide_legend(override.aes = list(color = c("black", "black"), fill = c("white", "white")))) + # 凡例の体裁:(凡例表示用) labs(title = "Word Distribution", subtitle = "iteration = {current_frame}", x = "v", y = expression(E(phi[kv]))) # gif画像を作成 gganimate::animate(plot = anime_word_graph, nframes = MaxIter+1, fps = 5, width = 900, height = 600)
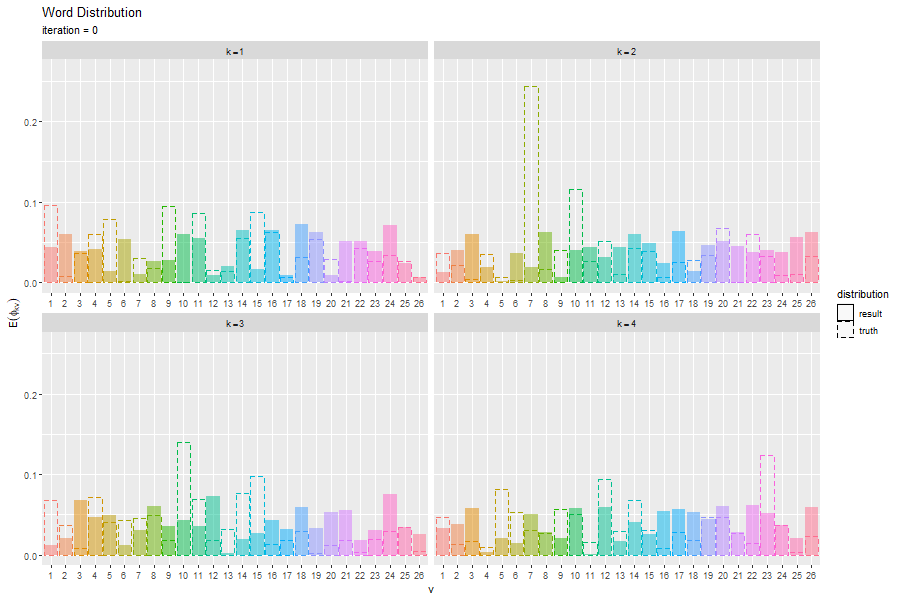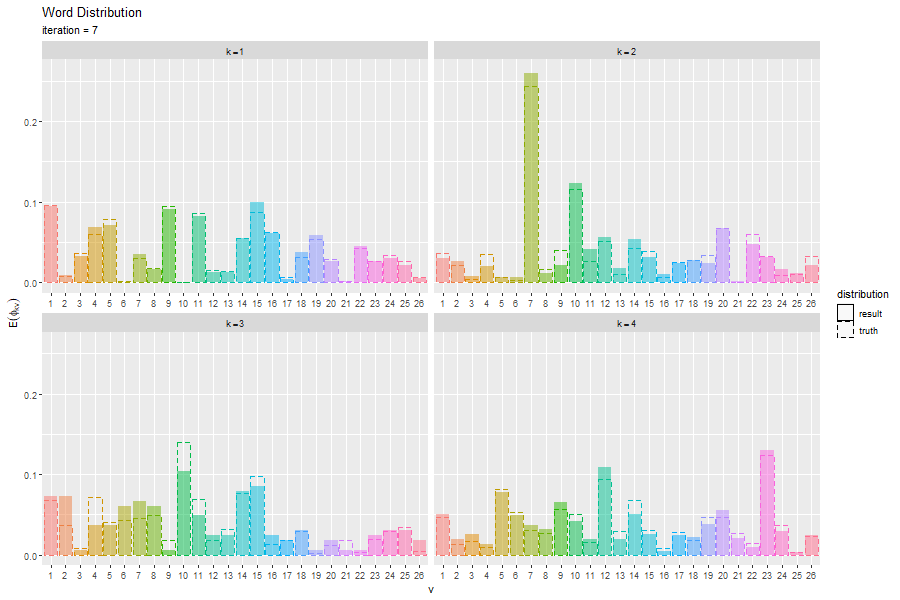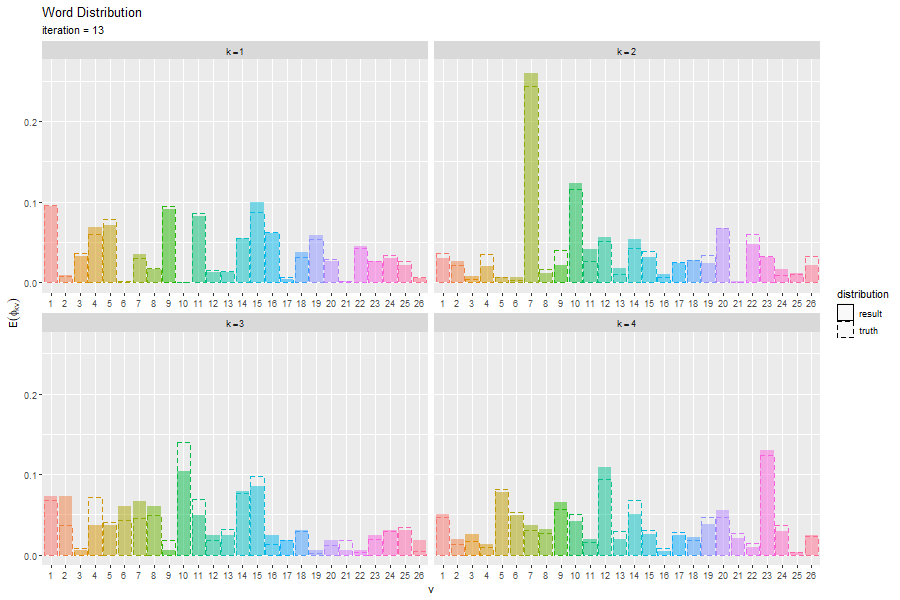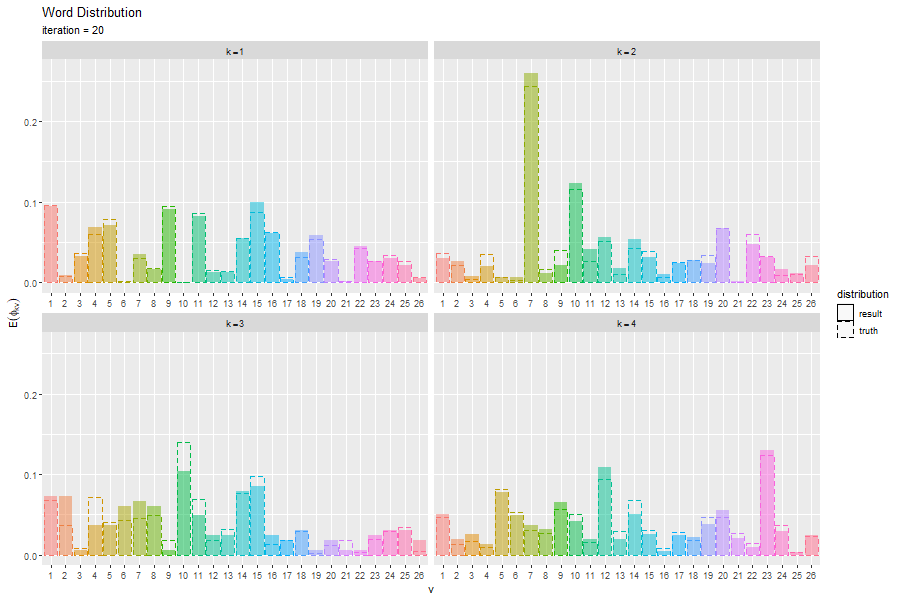
更新を繰り返すことで真の分布に近付く様子を確認できる。
この記事では、変分ベイズ推定を3重ループを使って実装した。次の記事では、ループを使わずに実装する。
参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
ディリクレ分布のパラメータはどれくらいの値をとるのだろうか。そういう勉強もしないといけないな。
2019/08/12:加筆修正しました。
2023.02.13:加筆修正しました。
(この本の2章でもやったはずでしたが、)その後別の本で、混合ではないカテゴリ分布の学習を導出・実装しました。
これによると、ハイパーパラメータの値は観測データに依存します。更新式を見ると分かる通り、データ数が多いとハイパーパラメータの値は大きくなります。
ハイパーパラメータの値の大小よりも、そのパラメータによる分布の形に注目するのがいいのだと思います。
この例では、変分事後分布のグラフを描くのは難しいので($V = 3$だと上の記事の様に可視化できる)、変分事後分布の期待値の形を見ています。
【次節の内容】