はじめに
機械学習プロフェッショナルシリーズの『トピックモデル』の勉強時に理解の助けになったことや勉強会用レジュメのまとめです。
この記事では、R言語でPLSA(確率的潜在意味解析)と呼ばれるトピックモデルをEMアルゴリズムを用いて最尤推定する方法について書いています。Rの基本的な関数で参考書のアルゴリズム4.1を組むことで、理論をコード・処理の面から理解しようというものです。
パラメータの更新式の導出などはこの記事をご参照ください。
【他の節一覧】
【この節の内容】
・コード全体
・テキスト処理
# 利用パッケージ library(RMeCab) library(tidyverse) ### テキスト処理 # 抽出しない単語を指定 stop_words <- "[a-z]" # 小文字のアルファベットを含む語 # 形態素解析 mecab_df <- docDF("フォルダ名", type = 1) # テキストファイルの保存先を指定する # 文書dの語彙vの出現回数(N_dv)の集合 N_dv <- mecab_df %>% filter(grepl("名詞|形容詞|^動詞", POS1)) %>% # 抽出する品詞(大分類)を指定する filter(grepl("一般|^自立", POS2)) %>% # 抽出する品詞(細分類)を指定する filter(!grepl(stop_words, TERM)) %>% # ストップワードを除く select(-c(TERM, POS1, POS2)) %>% # 数値列のみを残す filter(apply(., 1, sum) >= 5) %>% # 抽出する総出現回数を指定する t() # 転置 # 確認用の行列名 dimnames(N_dv) <- list(paste0("d=", 1:nrow(N_dv)), # 行名 paste0("v=", 1:ncol(N_dv))) # 列名 # 文書dの単語数(N_d)のベクトル N_d <- apply(N_dv, 1, sum) # 行方向に和をとる # 文書数(D) D <- nrow(N_dv) # 総語彙数(V) V <- ncol(N_dv)
・パラメータの初期設定
### パラメータの初期設定 # トピック数(K) K <- 4 # 任意の値を指定する # 負担率(q_dvk)の集合 q_dvk <- array(0, dim = c(D, V, K), dimnames = list(paste0("d=", 1:D), # 確認用の次元名 paste0("v=", 1:V), paste0("k=", 1:K))) ## トピック分布(theta_dk)の集合 # 値をランダムに付ける theta_dk <- sample(seq(0.1, 1, 0.01), D * K, replace = TRUE) %>% # ランダムな値を生成 matrix(nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 # 初期値の正規化 for(d in 1:D) { theta_dk[d, ] <- theta_dk[d, ] / sum(theta_dk[d, ]) } ## 単語分布(phi_kv)の集合 # 値をランダムに付ける phi_kv <- sample(seq(0, 1, 0.01), K * V, replace = TRUE) %>% # ランダムな値を生成 matrix(nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 paste0("V=", 1:V))) # 列名 # 初期値の正規化 for(k in 1:K) { phi_kv[k, ] <- phi_kv[k, ] / sum(phi_kv[k, ]) }
・最尤推定
# 推移の確認用 trace_theta <- theta_dk[1, ] trace_phi <- phi_kv[1, ] for(i in 1:50) { # 任意の回数を指定する # パラメータを初期化 next_theta_dk <- matrix(0, D, K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 next_phi_kv <- matrix(0, K, V, dimnames = list(paste0("k=", 1:K), # 行名 paste0("V=", 1:V))) # 列名 for(d in 1:D) { ## (各文書) for(v in 1:V) { ## (各語彙1) for(k in 1:K) { ## (各トピック) # 負担率を計算 tmp_q_numer <- theta_dk[d, k] * (phi_kv[k, v] ^ N_dv[d, v]) # 分子 tmp_q_denom <- sum(theta_dk[d, ] * (phi_kv[, v] ^ N_dv[d, v])) # 分母 q_dvk[d, v, k] <- tmp_q_numer / tmp_q_denom # theta_dkを更新 next_theta_dk[d, k] <- next_theta_dk[d, k] + q_dvk[d, v, k] * N_dv[d, v] for(v2 in 1:V) { ## (各語彙2) # phi_kvを更新 next_phi_kv[k, v2] <- next_phi_kv[k, v2] + q_dvk[d, v2, k] * N_dv[d, v2] } ## (/各語彙2) } ## (/各トピック) } ## (/各語彙1) } ## (/各文書) # パラメータを更新 theta_dk <- next_theta_dk phi_kv <- next_phi_kv # パラメータを正規化 for(d in 1:D) { theta_dk[d, ] <- theta_dk[d, ] / sum(theta_dk[d, ]) } for(k in 1:K) { phi_kv[k, ] <- phi_kv[k, ] / sum(phi_kv[k, ]) } # 推移の確認用 trace_theta <- rbind(trace_theta, theta_dk[1, ]) trace_phi <- rbind(trace_phi, phi_kv[1, ]) }
・コードの解説
・利用パッケージ
# 利用パッケージ library(RMeCab) library(tidyverse)
形態素解析のためのRMeCab::docDF()と、グラフ作成時のtidyr::gather()、ggplot2関連の関数以外にライブラリの読み込みが必要なのはdplyrのみ。(面倒なのでtidyversパッケージを読み込んでいる)
その他テキスト処理の部分は3.3節の記事を参照のこと。
・パラメータの初期設定
# トピック数(K) K <- 4 # 任意の値を指定する
任意のトピック数を指定する。
・負担率
# 負担率(q_dvk)の集合 q_dvk <- array(0, dim = c(D, V, K), dimnames = list(paste0("d=", 1:D), # 確認用の次元名 paste0("v=", 1:V), paste0("k=", 1:K)))
ここでは、単語レベルではなく語彙レベルで扱うため、$q_{dnk}$の変数名をq_dvkとする。
トピックモデルの負担率$q_{dvk}$は3次元の変数なので、array()を使って配列型として扱う。初期値0を全て0として、引数dim = c(D, V, K)で各次元の要素数を$D, V, K$個とする。
変数に付ける行列名等は目で確認するためのもので、付けなくても処理に影響しない。他の変数についても同様である。
・トピック分布
## トピック分布(theta_dk)の集合 # 値をランダムに付ける theta_dk <- sample(seq(0.1, 1, 0.01), D * K, replace = TRUE) %>% # ランダムな値を生成 matrix(nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 # 初期値の正規化 for(d in 1:D) { theta_dk[d, ] <- theta_dk[d, ] / sum(theta_dk[d, ]) }
まずは、ランダムな値を持つ$D$行$K$列の行列を作成する。
$\sum_{k=1}^K \theta_{dk} = 1$となるように正規化して初期値とする。
・単語分布
## 単語分布(phi_kv)の集合 # 値をランダムに付ける phi_kv <- sample(seq(0, 1, 0.01), K * V, replace = TRUE) %>% # ランダムな値を生成 matrix(nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 paste0("V=", 1:V))) # 列名 # 初期値の正規化 for(k in 1:K) { phi_kv[k, ] <- phi_kv[k, ] / sum(phi_kv[k, ]) }
同様に、$K$行$V$列の行列にランダムな値を割り振り、$\sum_{v=1}^V \phi_{kv} = 1$となるように正規化して初期値とする。
・最尤推定
ここからfor()ループ内の処理。
・パラメータの初期化
# パラメータを初期化 next_theta_dk <- matrix(0, nrow = D, ncol = K, dimnames = list(paste0("d=", 1:D), # 行名 paste0("k=", 1:K))) # 列名 next_phi_kv <- matrix(0, nrow = K, ncol = V, dimnames = list(paste0("k=", 1:K), # 行名 paste0("V=", 1:V))) # 列名
各パラメーターの更新時に用いる変数を作成する。
また、次ステップに入る前に初期化する。
・負担率の計算
# 負担率を計算 tmp_q_numer <- theta_dk[d, k] * (phi_kv[k, v] ^ N_dv[d, v]) # 分子 tmp_q_denom <- sum(theta_dk[d, ] * (phi_kv[, v] ^ N_dv[d, v])) # 分母 q_dvk[d, v, k] <- tmp_q_numer / tmp_q_denom
負担率は
$$
q_{dnk}
= \frac{
\theta_{dk} \phi_{kw_{dn}}
}{
\sum_{k'=1}^K \theta_{dk'} \phi_{k'w_{dn}}
}
\tag{4.1}
$$
の計算式に従って求める。ただし、この式は単語$w_{dn}$を使っているので、これを語彙$v$とするために各語彙の出現回数$N_{dv}$を用いて変換する。次のトピック分布・単語分布についても同様である。
$\phi_{kv}$は単語$v$の出現確率のことである。$N_{dv}$回出現する確率を考えると$\phi_{kv}^{N_{dv}}$となる。従って、計算式は
$$
q_{dvk} = \frac{\theta_{dk} \phi_{kv}^{N_{dv}} }{\sum_{k'=1}^K \theta_{dk'} \phi_{k'v}^{N_{dv}} }
$$
になる。
・トピック分布の更新
# theta_dkを更新 next_theta_dk[d, k] <- next_theta_dk[d, k] + q_dvk[d, v, k] * N_dv[d, v]
トピック分布の更新式(4.2)を語彙$v$に変換するには、負担率を$N_{dv}$回足し合わせればよい。すると、計算式は
$$
\theta_{dk}
= \frac{
\sum_{v=1}^V
q_{dvk} N_{dv}
}{
\sum_{k'=1}^K \sum_{v=1}^V
q_{dvk'} N_{dv}
}
$$
になる。この式の$\sum_{v=1}^V$の計算はfor(v in 1:V)の処理によって、初期値0のnext_theta_dkに$V$回繰り返しq_dvkを足すことで行われる。また、分母の$\sum_{k'=1}^K$については最後の正規化処理によって行う。
・単語分布の更新
for(v2 in 1:V) { # phi_kvを更新 next_phi_kv[k, v2] <- next_phi_kv[k, v2] + q_dvk[d, v2, k] * N_dv[d, v2] }
同様に、単語分布の更新式(4.3)を語彙$v$に変換すると、更新式は
$$
\phi_{kv}
= \frac{
\sum_{d=1}^D
q_{dvk} N_{dv}
}{
\sum_{v'=1}^V \sum_{d=1}^D
q_{dv'k} N_{dv'}
}
$$
になる。初期値0のnext_phi_kvに$D$回q_{dvk}を足すことで分子の計算を行う。分母の計算については次の正規化処理で行う。
・パラメータの正規化
# パラメータを更新 theta_dk <- next_theta_dk phi_kv <- next_phi_kv # パラメータを正規化 for(d2 in 1:nrow(theta_dk)) { theta_dk[d2, ] <- theta_dk[d2, ] / sum(theta_dk[d2, ]) } for(k2 in 1:nrow(phi_kv)) { phi_kv[k2, ] <- phi_kv[k2, ] / sum(phi_kv[k2, ]) }
各パラメータを次ステップの計算に用いるために移す。
更新された変数をそれぞれ$\sum_{k=1}^K \theta_{dk} = \sum_{v=1}^V \phi_{kv} = 1$の条件に満たすように正規化する。
この推定処理を指定した回数繰り返す。(本当は収束条件を満たすまで繰り返すようにしたい…)
・パラメータの推定結果の確認
・トピック分布
## トピック分布 # データフレームを作成 theta_df_wide <- cbind(as.data.frame(theta_dk), as.factor(1:D)) # 文書番号 # データフレームをlong型に変換 colnames(theta_df_wide) <- c(1:K, "doc") # key用の行名を付与 theta_df_long <- gather(theta_df_wide, key = "topic", value = "prob", -doc) # 変換 # 描画 ggplot(data = theta_df_long, mapping = aes(x = topic, y = prob, fill = topic)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ doc, labeller = label_both) + # グラフの分割 labs(title = "Probabilistic Latent Semantic Analysis") # タイトル
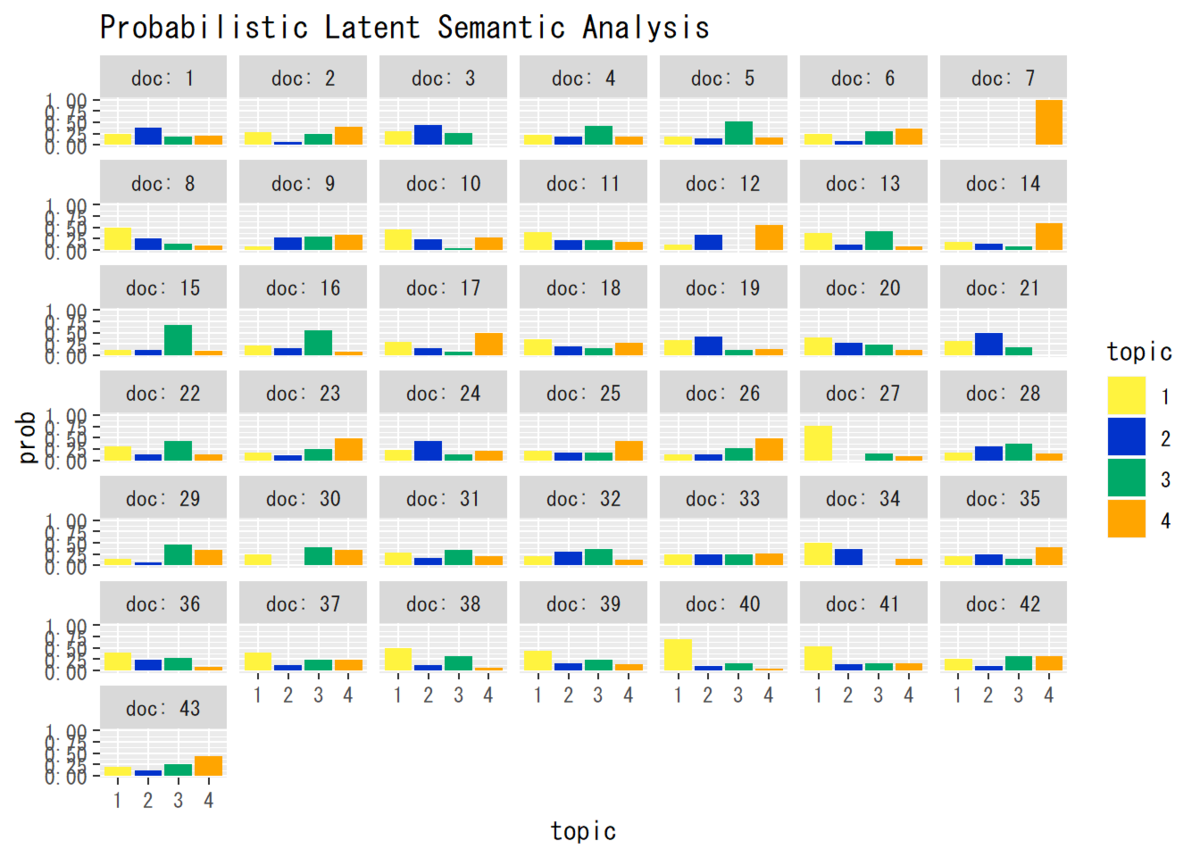
・単語分布
## 単語分布 # データフレームを作成 phi_df_wide <- cbind(as.data.frame(t(phi_kv)), as.factor(1:V)) # 語彙番号 # データフレームをlong型に変換 colnames(phi_df_wide) <- c(1:K, "word") # key用の行名を付与 phi_df_long <- gather(phi_df_wide, key = "topic", value = "prob", -word) # 変換 # 描画 ggplot(data = phi_df_long, mapping = aes(x = word, y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ facet_wrap( ~ topic, labeller = label_both) + # グラフの分割 theme(legend.position = "none") + # 凡例 labs(title = "Probabilistic Latent Semantic Alanysis") # タイトル
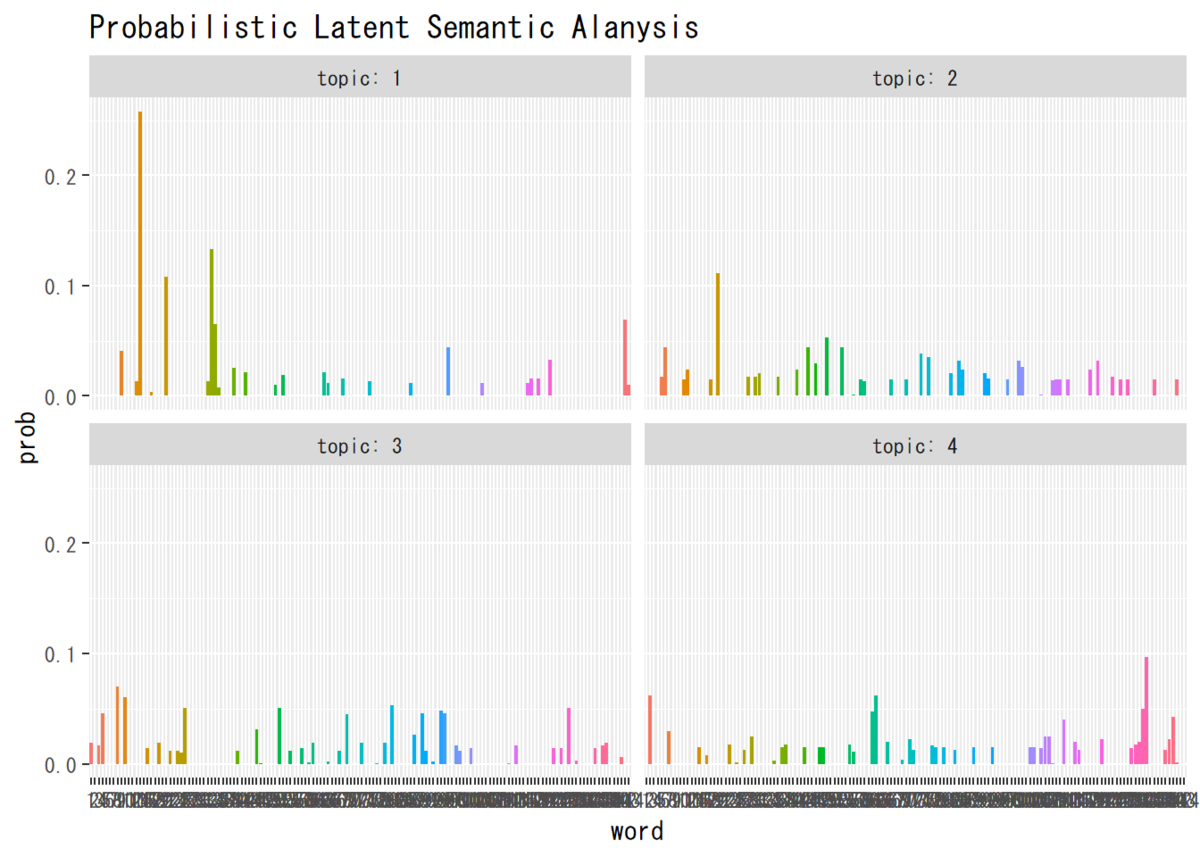
・推移の確認
・推移の記録
# 推移の確認用(初期値) trace_theta <- theta_dk[1, ] trace_phi <- phi_kv[1, ] # 推移の確認用(更新後) trace_theta <- rbind(trace_theta, theta_dk[1, ]) trace_phi <- rbind(trace_phi, phi_kv[1, ])
推移を確認するために、パラメータを更新する度に記録しておく。トピック分布については文書1、単語分布についてはトピック1のみ確認する。
・トピック分布
## トピック分布 # データフレームを作成 theta_df_wide <- cbind(as.data.frame(trace_theta), 1:nrow(trace_theta)) # 試行回数 # データフレームをlong型に変換 colnames(theta_df_wide) <- c(1:K, "n") # key用の行名を付与 theta_df_long <- gather(theta_df_wide, key = "topic", value = "prob", -n) # 変換 # 描画 ggplot(data = theta_df_long, mapping = aes(x = n, y = prob, color = topic)) + # データ geom_line() + # 折れ線グラフ labs(title = "theta:PLSA") # タイトル
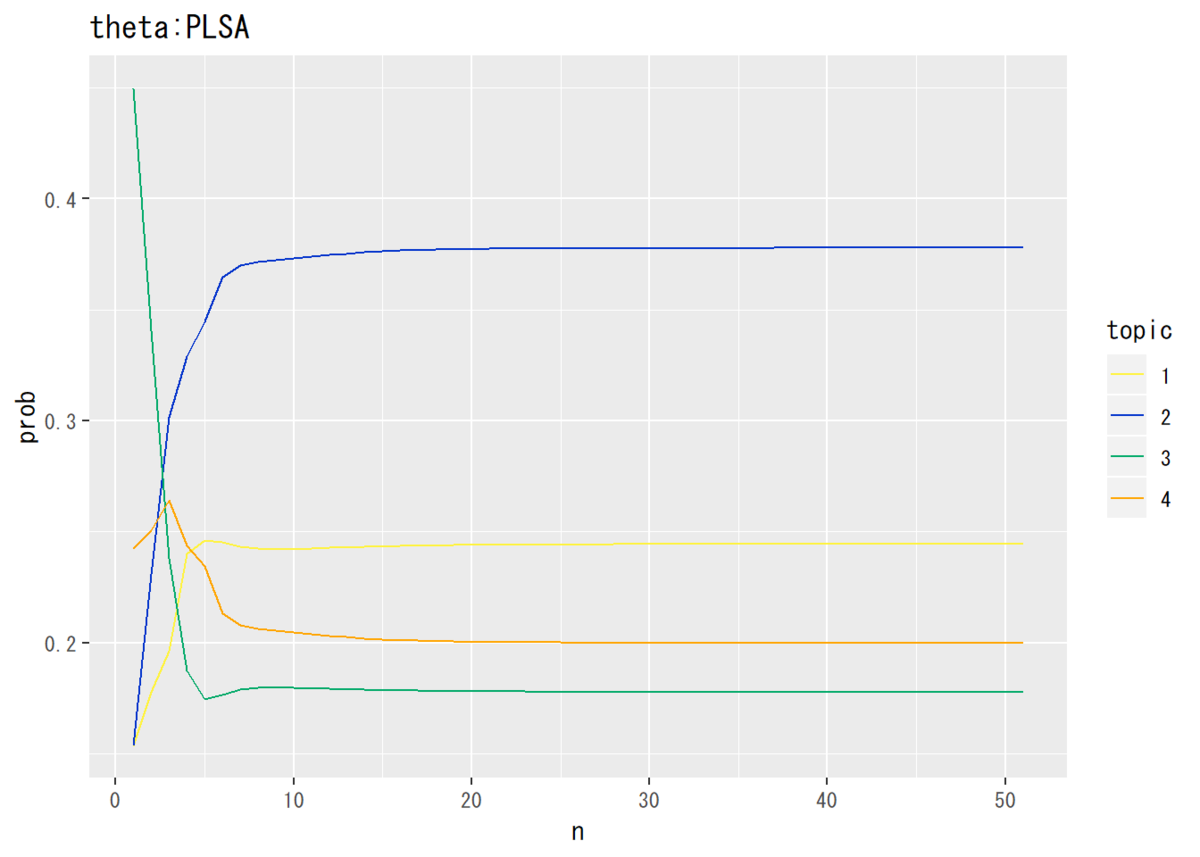
・単語分布
## 単語分布 # データフレームを作成 phi_df_wide <- cbind(as.data.frame(trace_phi), 1:nrow(trace_phi)) # 試行回数 # データフレームをlong型に変換 colnames(phi_df_wide) <- c(1:V, "n") # key用の行名を付与 phi_df_long <- gather(phi_df_wide, key = "word", value = "prob", -n) # 変換 # 描画 ggplot(data = phi_df_long, mapping = aes(x = n, y = prob, color = word)) + # データ geom_line(alpha = 0.5) + # 折れ線グラフ theme(legend.position = "none") + # 凡例 labs(title = "phi:PLSA") # タイトル
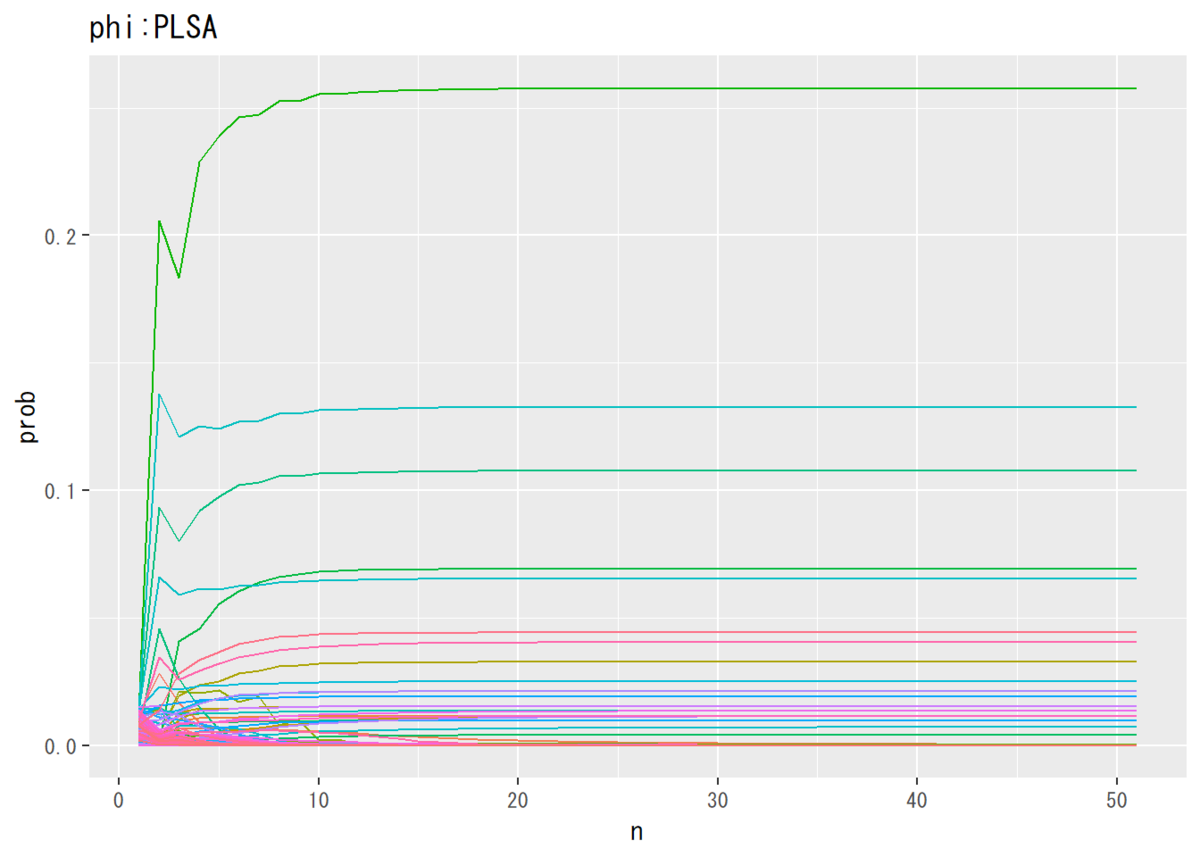
・各トピックの出現確率の上位語の確認
### 各トピックの出現確率の上位語 ## 語彙インデックス(v) # 指定した出現回数以上の単語の行番号 num <- mecab_df %>% select(-c(TERM, POS1, POS2)) %>% apply(1, sum) >= 5 # 抽出する総出現回数を指定する v_index <- mecab_df[num, ] %>% filter(grepl("名詞|形容詞|^動詞", POS1)) %>% # 抽出する品詞を指定する filter(grepl("一般|^自立", POS2)) %>% filter(!grepl(stop_words, TERM)) %>% .[, 1] # 単語の列を抽出する # データフレームを作成 phi_df_wide2 <- cbind(as.data.frame(t(phi_kv)), v_index) %>% as.data.frame() colnames(phi_df_wide2) <- c(paste0("topic", 1:K), "word") # key用の行名を付与 # データフレームの整形 phi_df_long2 <- data.frame() for(i in 1:K) { tmp_df <- phi_df_wide2 %>% select(paste0("topic", i), word) %>% arrange(-.[, 1]) %>% # 降順に並べ替え head(20) %>% # 任意で指定した上位n語を抽出 gather(key = "topic", value = "prob", -word) # long型に変換 phi_df_long2 <- rbind(phi_df_long2, tmp_df) } # 描画 ggplot(data = phi_df_long2, mapping = aes(x = reorder(x = word, X = prob), y = prob, fill = word)) + # データ geom_bar(stat = "identity", position = "dodge") + # 棒グラフ coord_flip() + # グラフの向き facet_wrap( ~ topic, scales = "free") + # グラフの分割 theme(legend.position = "none") + # 凡例 labs(title = "Mixture of Unigram Models:VBE") # タイトル
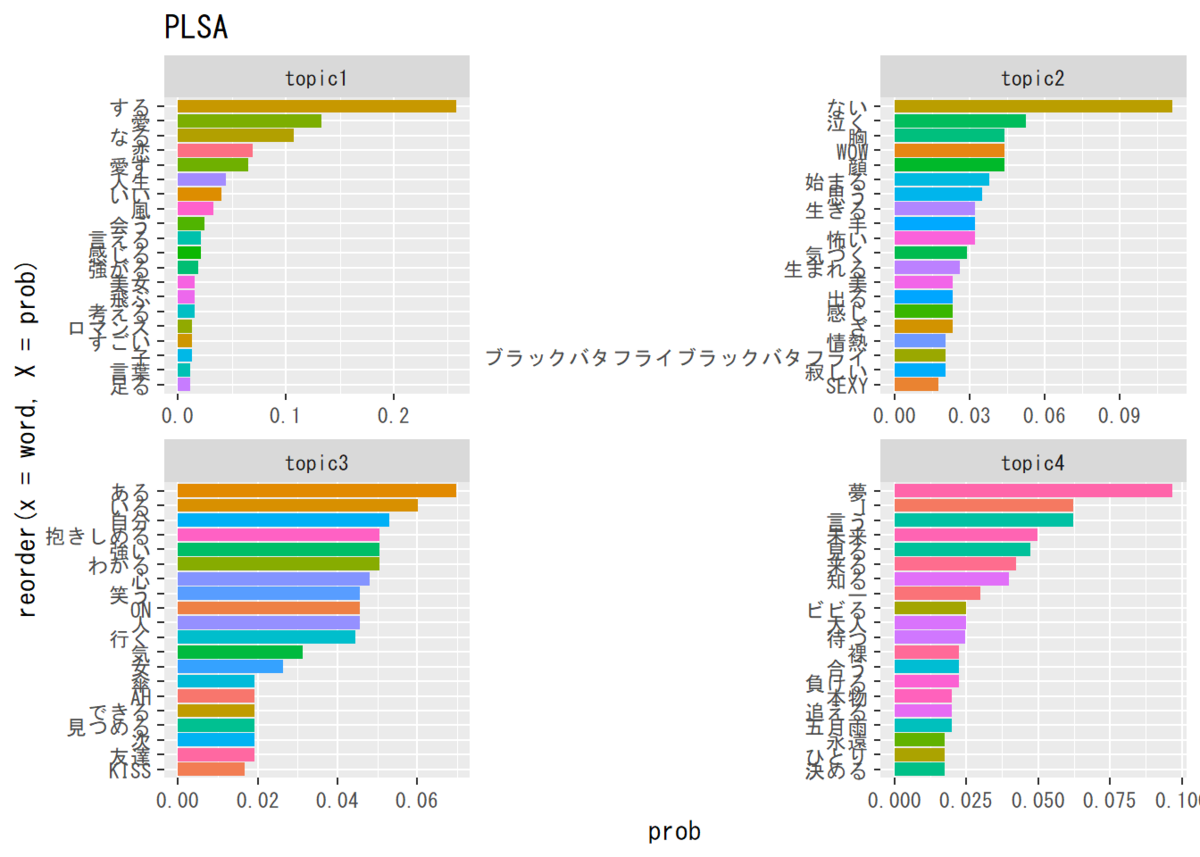
(まぁ、分析自体については追々です。)
参考書籍
- 岩田具治(2015)『トピックモデル』(機械学習プロフェッショナルシリーズ)講談社
おわりに
3・4章のアルゴリズムで最初に組めたのがこれ。びっくり！ところで、どうやって検証すればよいのですかねぇ？？
2019/08/13：加筆修正しました。
【次節の内容】
